MABAC method for multiple attribute group decision making under qrung orthopair fuzzy environment

Jie Wng ,Guiwu Wei ,*,Cun Wei ,b,Yu Wei

a School of Business,Sichuan Normal University,Chengdu,610101,PR China

b School of Statistics,Southwestern University of Finance and Economics,Chengdu,611130,PR China

c School of Finance,Yunnan University of Finance and Economics,Kunming,650221,PR China

Keywords:MAGDM problems Q-rung orthopair fuzzy sets(q-ROFSs)MABAC model Q-rung orthopair fuzzy weighted average(q-ROFWA)operators Q-rung orthopair fuzzy weighted geometric(q-ROFWG)operators Q-ROFNs MABAC model Construction project

ABSTRACT As the generalization of intuitionistic fuzzy set(IFS)and Pythagorean fuzzy set(PFS),the q-rung orthopair fuzzy set(q-ROFS)has emerged as a more meaningful and effective tool to solve multiple attribute group decision making(MAGDM)problems in management and scientific domains.The MABAC(multi-attributive border approximation area comparison)model,which handles the complex and uncertain decision making issues by computing the distance between each alternative and the bored approximation area(BAA),has been investigated by an increasing number of researchers more recent years.In our article,consider the conventional MABAC model and some fundamental theories of q-rung orthopair fuzzy set(q-ROFS),we shall introduce the q-rung orthopair fuzzy MABAC model to solve MADM problems.at first,we briefly review some basic theories related to q-ROFS and conventional MABAC model.Furthermore,the q-rung orthopair fuzzy MABAC model is built and the decision making steps are described.In the end,An actual MADM application has been given to testify this new model and some comparisons between this novel MABAC model and two q-ROFNs aggregation operators are provided to further demonstrate the merits of the q-rung orthopair fuzzy MABAC model.©2020 China Ordnance Society.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.This is an open access article under the CCBY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1.Introduction

With the gradual progress of urbanization in china,the number of construction projects under construction has increased.Thus,It is very important to evaluate the safety of construction projects.As we all know,the construction industry is related to national economic development and social stability,and the safety of the construction industry has always been a high concern of the government[1].Construction projects are characterized by complex construction conditions,multiple safety influencing factors and harsh environment.It is a feasible measure to clarify the hazard sources and hazard factors in construction sites to improve the effectiveness of safety management in construction sites.The safety work in the construction industry is a high concern of the government[2].At the present stage,the state has clarified the safety management system of the construction industry from the two aspects of the legal system and technical system.After the establishment of the responsibility system for production safety,the responsibility and power of the management staff at all levels of the enterprise have been clearly defined.In the construction process of the enterprise,the safety issue is also taken as a key concern.Some construction enterprises have set up special inspection organizations in construction management to control the occurrence of safety accidents by means of self-examination and self-correction.In the implementation process of safety inspection,some enterprises have built a combination of regular inspection and regular inspection.The construction of safety management system with the participation of enterprises,the state and the masses can also provide guarantee for the development of construction safety management[3-5].(see Fig.1)

In previous works,some scholars studied the construction projects by a varity of decision making tools,such as:the CODAS method[6],the fuzzy comprehensive evaluation and TOPSIS[7],aggregation operators[8],VIKOR model[9]and so on.Through the analysis of the existing safety evaluation methods in the construction industry,there are some problems in the following aspects of construction management in the construction industry.First,in the aspect of safety evaluation technology,the existing safety evaluation methods have some technical problems.Secondly,inaccurate evaluation results and strong subjectivity of staff are also prominent problems in the safety evaluation methods of the construction industry.Thus,it is important to find a good way to express assessment information and utilize the suitable tool to derive reasonable assessment results.

Fig.1.The relationship between IFS,PFS,and q-ROFS.

For the indeterminacy of DM's and the decision-making issues,we always cannot give accuracy evaluation values of alternatives to select the best project in real MADM problems.To conquer this disadvantage,fuzzy set theory which defined by Zadeh[10]in 1965 originally used the membership function to describe the estimation results rather than exact real-number.Atanassov[11,12]presented another measurement index which named non-membership function as a complement.More recently,in order to extend the scope of evaluation information,the Pythagorean fuzzy set(PFS)[13,14]has been defined to deal with more complicated MADM problems,the prominent characteristic of the PFS is the sum of squares of membership and non-membership is limited to 1.Motivated by IFSand PFS,Yager[15]introduced the concept of the q-rung orthopair fuzzy set(q-ROFS),the characteristic of the q-ROFS is the sum of the q-th power of the membership and nonmembership is limited 1,that is to say,μq+vq≤1.when q= 1,the q-ROFS will degrade into IFS,when q=2,the q-ROFS will degrade into PFS.Thus,the q-ROFS is a good way to express assessment information.In addition,to date,The MABAC(multiattributive border approximation area comparison)model,which originally defined by Pamucar and Cirovic[16]in 2015,computes the distance measure between each alternatives and the bored approximation area(BAA)and has a large amount of precious characteristics such as:(1)the computing results by MABAC method are stable;(2)the calculating equations are simple;(3)it takes the latent values of gains and losses into account;(4)it is available to combine this model with other approaches.Hence,the MABAC method is a good tool to derive reasonable decision making results.

The mainly novelty and contribution of this paper is proposing the q-ROFMABAC model.On the one hand,the q-ROFS can express more fuzzy information,on the other hand,the MABAC model has four precious merits mentioned above.Thus,we can derive accuracy assessment results for construction project by utilizing the q-ROF MABAC model.In order to elaborate the process of putting forward the q-ROFMABAC model,this manuscript is structured as:section 2 review s some works about the decision making model and fuzzy set theory.section 3 simply describes some preliminary know ledge and aggregation operators related to the q-ROFSs.Section 4 presents the computing steps of conventional MABAC model in detail.On account of the conventional MABAC model and the q-ROFNs information,Section 5 builds the q-rung orthopair fuzzy MABAC model.An actual MADM application has been given to testify this new model and some comparisons between this novel MABAC model and two q-ROFNs aggregation operators are provided to further demonstrate the merits of the q-rung orthopair fuzzy MABAC model in Section 6.Section 7 gives some conclusions of our works.

2.Related work

In previous work,lots of decision-making model such as the VIKOR method[17-20],the ELECTRE method[21-23],the TOPSIS method[24-26],the PROMETHEE method[27],the GRA method[28-30],the EDAS model[31]and the TODIM model[32-35]had been studied extensively by numerous of investigators.Compare with the existed literature,the precious advantage of MABAC model[36,37]is that it takes into account the distance between alternative schemes and the bored approximation area(BAA),and considers the indeterminacy of decision makers and the fuzziness of decision environment,so as to derive more accurate and effective decision making results.Pamucar and Cirovic[16]originally defined the MABAC method and studied it with the problems of the selection of transportation and loading and unloading resources for logistics centers.Then,Peng and Yang[38]combined the MABAC model with Pythagorean fuzzy Choquet integral.Yu,Wang and Wang[39]studied the hotels selection on a tourism website by using an interval type-2 fuzzy likelihood-based MABAC model.Xue,You,Lai and Liu[40]proposed an new interval-valued intuitionistic fuzzy MABACmodel with incomplete weight information.Peng and Dai[41]presented a novel MABAC model to study some MADM approaches under single-valued neutrosophic environment.Gigovic,Pamucar,Bozanic and Ljubojevic[42]provided the GIS-DANPMABAC model for solving MADM problems.Based on the projection measure and the hesitant fuzzy linguistic term set,Sun,Hu,Zhou and Chen[43]built the hesitant fuzzy linguistic projectionbased MABAC model.Based on the picture 2-tuple linguistic variables,Zhang,Gao,Wei,Wei and Wei[44]studied the MABAC method and built decision making model to deal with MADM.Bojanic,Kovaˇc,Bojanic and Ristic[45]gave the hybrid multi-criteria decision-making model in a defensive operation of the guided antitank missile battery based on the fuzzy AHP-MABAC.Veskovi'c,Stevi'c,Stoji'c,Vasiljevi'c and Milinkovic[46]evaluated the railway management model by using DELPHI-SWARA-MABAC model.Boˇzani'c,Pamuˇcar and Karovic[47]applied the MABAC method in support of MADM for the use of force in a defensive operation.Pamucar,Petrovic and Cirovic[48]defined the modification of the Best-Worst and MABAC methods with interval-valued fuzzy-rough numbers.

As for the PFS,Zhang and Xu[49]defined the Pythagorean fuzzy TOPSIS model to handle the MADM problems.Peng and Yang[50]primarily proposed two Pythagorean fuzzy operations including the division and subtraction operations to better understand PFS.Gou,Xu and Ren[51]studied some precious properties of continuous Pythagorean fuzzy information.Reformat and Yager[52]handled the collaborative-based recommender system with Pythagorean fuzzy information.Garg[53]defined some new Pythagorean fuzzy aggregation operators to fuse Pythagorean fuzzy numbers(PFNs).Tang,Wei and Gao[54]combined the interval valued Pythagorean fuzzy set and the Muirhead mean(MM)operators to define some novel aggregation operators for MADM.Wang,Gao and Wei[55]discussed some Dice similarity measures between Pythagorean fuzzy set and built the decision making model to select suitable ERP system.Tang and Wei[56]given some novel Bonferroni mean(BM)operators,generalized Bonferroni mean(GBM)operators,dual generalized Bonferroni mean(DGBM)operators under dual hesitant Pythagorean fuzzy environment.Tang,Wang,Lu,Wei,Wei and Wei[57]utilized generalized Heronian mean(GHM)operator to fuse dual hesitant Pythagorean fuzzy variables and developed some novel aggregation operators.According to hesitant Pythagorean fuzzy set and the Maclaurin symmetric mean(MSM)operator,Garg[58]proposed some hesitant Pythagorean fuzzy Maclaurin symmetric mean operator for MADM.Considered the advantage of the Dombi operation law s,Khan,Ashraf,Abdullah,Qiyas,Luo and Khan[59]defined some Pythagorean fuzzy Dombi operators to deal with actual MADM applications.Biswas and Sarkar[60]established the interval-valued Pythagorean fuzzy TODIM model.Zhu and Li[61]presented some Pythagorean fuzzy Muirhead mean(MM)operators.Wang,Weiand Gao[62]introduced some MSM operators under the intervalvalued 2-tuple linguistic Pythagorean fuzzy environment.Based on the entropy measure,Biswas and Sarkar[63]built the Pythagorean fuzzy TOPSIS model to handle MADM with incomplete weight information.Yang and Pang[64]gave the concept of the hesitant interval-valued Pythagorean fuzzy set(HIVPFS)and proposed the hesitant interval-valued Pythagorean fuzzy VIKOR method.

In terms of the q-ROFS,Liu and Wang[65]discussed the weighted average(WA)operator and the weighted geometric(WG)operator under the q-ROFSand given some aggregation operator to fuse the q-rung orthopair fuzzy numbers(q-ROFNs).To consider the interrelationship between any number of being fused elements,Wei,Wei,Wang,Gao and Wei[66]introduced four MSM operators to fuse q-rung orthopair fuzzy information,including the q-ROFMSM operator,the q-ROFWMSM operator,the q-ROFDMSM operator and the q-ROFWDMSM operator.Wei,Gao and Wei[67]developed the q-rung orthopair fuzzy Heronian mean operators and the q-rung orthopair 2-tuple linguistic Heronian mean operators to deal with MADM.Yang and Pang[68]presented some qrung orthopair fuzz partitioned Bonferroni mean operators.Based on the q-rung interval-valued fuzzy set and the Hamy mean operator,Wang,Gao,Wei and Wei[69]proposed some aggregation operators.Liu and Liu[70]defined the linguistic q-rung orthopair fuzzy set(Lq-ROFS)and gave some linguistic q-rung orthopair fuzzy power Bonferroni mean operators.Xu,Shang,Wang,Wu and Huang[71]introduced the concept of q-rung dual hesitant orthopair fuzzy set(q-RDHOFS)and presented some novel Heronian mean operators under this fuzzy environment.Wang,Wang,Wei and Wei[72]discussed some cosine and cotangent similarity measures between any two q-ROFSs.

How ever,it's clear that the study about the MABAC model with q-ROFNs information is not existed.Hence,it's necessary to discuss the q-rung orthopair fuzzy MABAC model.The goal of this paper is to develop a novel MABAC method based on the conventional MABAC model and q-rung orthopair fuzzy information to study MADM problems more effectively.

3.Preliminaries

3.1.The q-rung orthopair fuzzy set

In this part,as the generalization of the IFS and the PFS,some fundamental theories of the q-ROFS are shown as below.

Def inition 1.[15].Assume that X beafix set.The q-ROFS can be depicted as

where the μP:X→［0，1］indicates the membership degree,the νP:X→［0，1］indicates the non-membership degree which satisfies

The indeterminacy degree can be calculatedFor convenience,we called p=（μ，ν）a q-ROFN.

Def inition 2.[65].Given p=（μ，v）as a q-ROFN,the q-rung orthopair fuzzy score results can be computed by following equation:

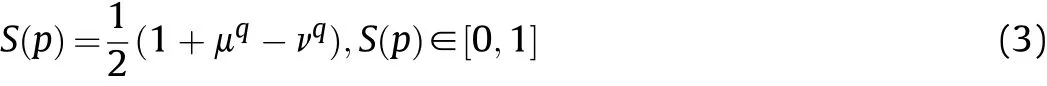
Def inition 3.[65].Given p=（μ，ν）as a q-ROFN,the q-rung orthopair fuzzy accuracy results can be computed by following equation:

Def inition 4.[65].Given p1=（μ1，ν1）and p2=（μ2，ν2）be any two q-ROFNs,qqandindicates the score results of p1and p2,H（p1）=（μ1）q+（ν1）qand H（p2）=（μ2）q+（ν2）qindicates the accuracy results of p1and p2,respectively,then if S（p1）＜S（p2）,then p1＜p2;if S（p1）=S（p2）,then(1)if H（p1）=H（p2）,then p1=p2;(2)if H（p1）＜H（p2）,p1＜p2.

Def inition 5.[65].Given p1=（μ1，ν1）,p2=（μ2，ν2）,and p=（μ，ν）be any three q-ROFNs,then some basic operation law s can be depicted as:

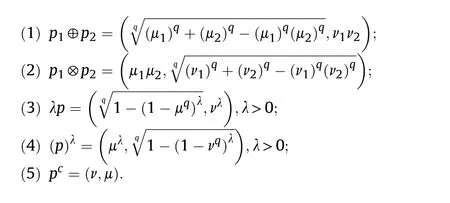
3.2.Some q-rung orthopair fuzzy aggregation operators

Def inition 6.[65].Let pj=（μj，νj）（j=1，2，…，n）be a list of q-ROFNs,then the q-ROFWA operator and the q-ROFWG)operator can be expressed as:

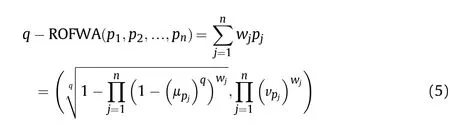
and

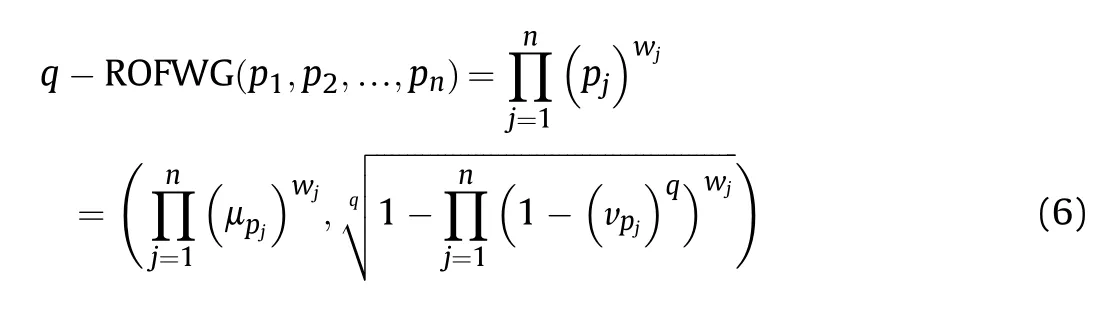
where wjis weighting vector of pj，j=1，2，…，n.which satisfies.

Definition 7.Let p1=（μ1，ν1）and p2=（μ2，ν2）be two q-ROFNs,then we can obtain the q-rung orthopair fuzzy normalized Hamming distance(q-ROFNHD)as:

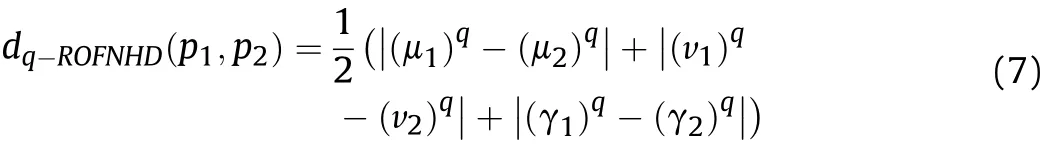
4.The conventional MABAC model

Suppose there are m alternatives｛A1，A2，…，Am｝,n attributes｛G1，G2，…，Gn｝with weighting vector be wj（j=1，2，…，n）and λ experts｛d1，d2，…，dλ｝with weighting vector be｛ω1，ω2，…，ωλ｝,then the decision-making procedures of the conventional MABAC model are expressed as below.

Step 1. Construct the evaluation matrix

Step 2.According to some aggregation operators,we can utilize overallto Aij;

Step 3. Normalize the fused results matrix r=i=1，2，…，m，j=1，2，…，n based on the type of each attributes by following formula;

For benefit attributes:

For cost attributes:

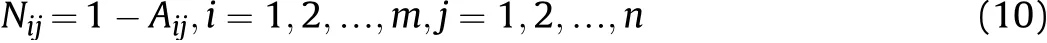
Step 4.According to the normalized matrix Nij（i=1，2，…，m，j=1，2，…，n）and attribute's weights wj（j=1，2，…，n）,the weighted normalized matrix WNij，i=1，2，…，m，j=1，2，…，n can be computed as:

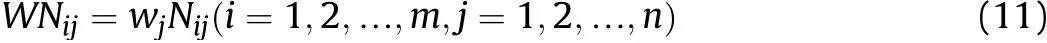
Step 5.Calculate the values of border approximation area(BAA)and the BAA matrix G=can be constructed as follow s;

Step 6.Calculate the distancebetween each alternative and the BAA by follow ing equation;

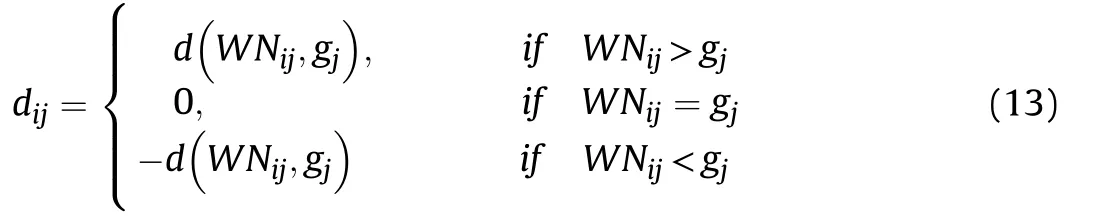
where d（WNij，gj）means the distance from WNijto gj.According to the values of dij,we can get:

(1)if dij＞0,the alternatives belong to the upper approximation area G+(UAA);

(2)if dij=0,the alternatives belong to the border approximation area G(BAA);

(3)if dij＜0,the alternatives belong to the lower approximation area G-(LAA).

Obviously,the best alternatives are included in G+(UAA)and the worst alternatives are included in G-(LAA).

Step 7.Sum the values of each alternative's dijby following equation;

On account of the comprehensive evaluation result Si,the order of all alternatives can be deirved,clearly,the bigger the comprehensive evaluation result Si,the better the choice.

5.The MABAC model with q-ROFNs

Although the IFS and PFS have been applied in many fields of decision making problems,how ever,there are some special situations that IFS and PFS cannot deal with.For instance,when the fuzzy information given by experts are shown as(0.7,0.8)which indicates that the membership degree is 0.7 and the nonmembership is 0.8,obviously,both IFS and PFS can't satisfy this situation.As the extension of the two fuzzy sets,q-ROFS is more effective and scientific to solve more complex and uncertain problems.based on the conventional MABAC method and the qrung orthopair fuzzy information;we can build the q-rung orthopair fuzzy MABAC model which all the evaluation information are depicted by q-ROFNs.

Suppose there are m alternatives｛A1，A2，…，Am｝,n attributes｛G1，G2，…，Gn｝ with weighting vector be wj（j=1，2，…，n）and λ experts｛d1，d2，…，dλ｝with weighting vector be｛ω1，ω2，…，ωλ｝,given the q-rung orthopair fuzzy evaluation matrix R==（），i=1，2，…，m，j=1，2，…，n，∈［0，1］indicates the membership degree,vλij∈［0，1］indicates the membership degree,then the decision-making steps of q-rung orthopair fuzzy MABAC model can expressed as follow s.

Step 1.Establish the q-rung orthopair fuzzy evaluation matrix R=，i=1，2，…，m，j=1，2，…，n as below.

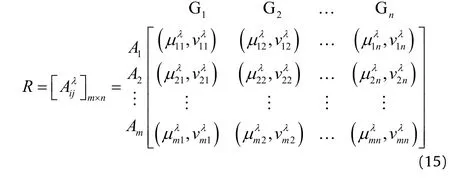
Step 2.According to the q-ROFWA or q-ROFWG aggregation operators,we can utilize overallto Aij,the fused q-ROFNs matrix r=shown as follow s;

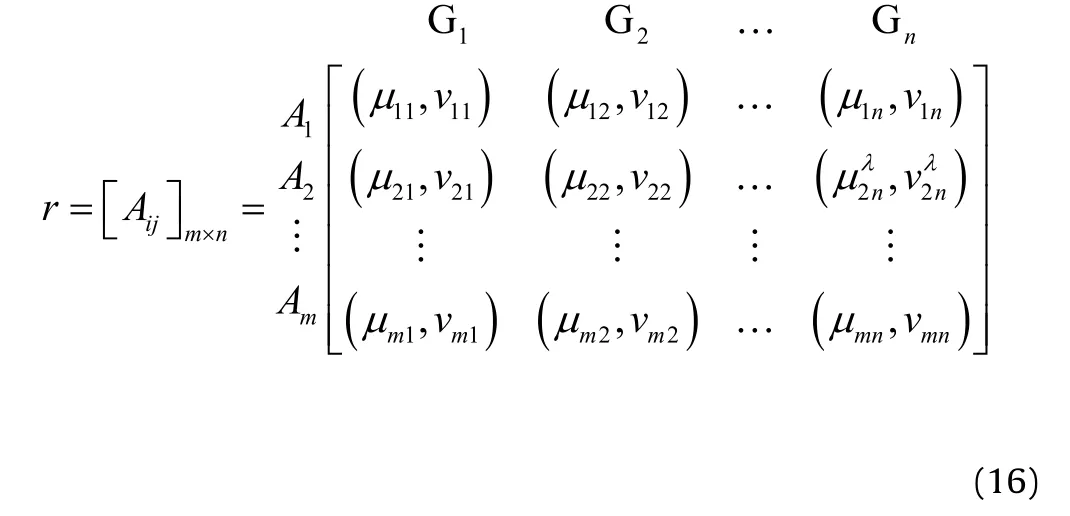
where Aij=（μij，vij）（i=1，2，…，m，j=1，2，…，n）denotes the fused q-rung orthopair fuzzy information of alternative Ai（i=1，2，…，m）on attribute Gj（j=1，2，…，n）.

Step 3. Normalize the matrix r=［Aij］m×n，i=1，2，…，m，j=1，2，…，n based on the type of each attribute by follow ing formula;

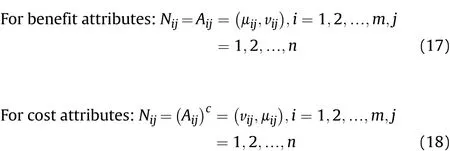
Step 4. According to the normalized matrix Nij=（μij，vij）（i=1，2，…，m，j=1，2，…，n） and at tribute's weighting vector wj（j=1，2，…，n）,the fuzzy weighted normalized matrix WNij=（μ′ij，v′ij）（i=1，2，…，m，j=1，2，…，n）can be computed as:

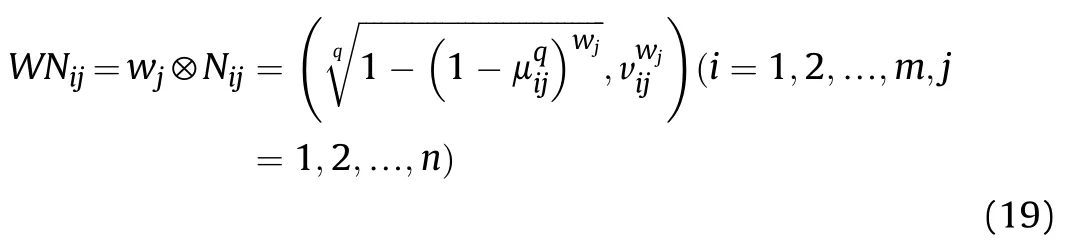
Step 5.Compute the values of BAA and the BAA matrix G=［gj］1×ncan be constructed as follow s;

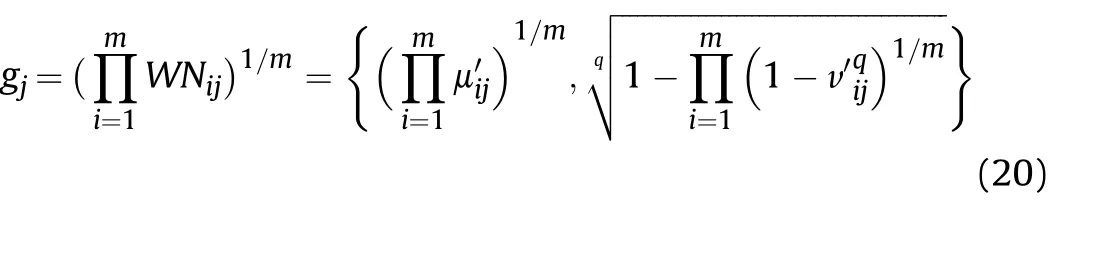
Step 6.Compute the distance D=［dij］m×nbetween alternatives and the BAA by following equation;

where d（WNij，gj）means the distance from WNijto gjwhich can be calculated by Eq.(7).

Step 7.Sum the values of each alternative's dijby following equation;

On account of the comprehensive evaluation result Si,the order of all alternatives can be deirved,clearly,the bigger the comprehensive evaluation result Si,the better the choice.

From above decision making steps,we can obtain that the qrung orthopair fuzzy MABAC model can deal with more complicated and fuzzy problems,which indicates that this method is more suitable to applied in management activities,and can promote the development of management field and enrich the research of management theory.

6.The numerical example

6.1.Numerical for q-ROFNs MAGDM problems

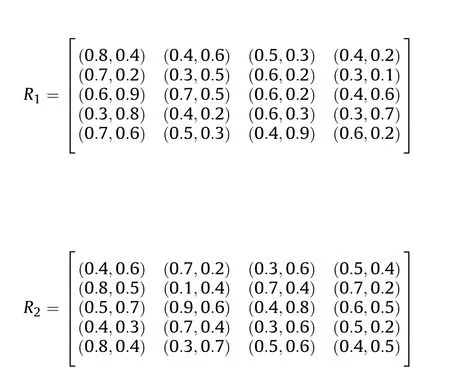
In this part,we give an actual decision making application to select best construction projects by using the q-rung orthopair fuzzy MABAC model.Assume that five possible construction projects Ai（i=1，2，3，4，5）(five construction companies with different construction advantages)to be selected and four attributes to evaluate these construction projects:①G1is the human factors in construction projects;②G2is the energy cost factors;③G3is the building materials and equipment factors;④G4is the environmental factors. The five possible construction projects Ai（i=1，2，3，4，5）are to be evaluated with q-ROFNs with the four criteria by three experts(scholars and professors with many years of experience in construction project and fuzzy set theory)dλ(Suppose expert's weighting vector is（0.25，0.45，0.30）and at tribute's weighting vector is（0.16，0.32，0.28，0.24）).

Step 1.Given the q-rung orthopair fuzzy evaluation matrix R=，i=1，2，…，m，j=1，2，…，n as below.

Step 2.Then according to q-ROFWA operator and expert's weights, we can utilize overall Aλijto Aijobtain the matrix r=［Aij］m×n，i=1，2，…，m，j=1，2，…，n as below.(suppose q=3，take the A11for example)

Similarly,we can derive other computing results,thus,all the results are list in R as below.

Step 3.Normalize the fused results matrix R=［Aij］m×n，i=1，2，…，m，j=1，2，…，n based on the type of each attributes by Eqs.(17)and(18);(G2is the cost attribute)

For G2is the cost attribute,thus,the A12，A22，A32，A42，A52need to be normalized,for instance N12=（A12）c=（0.5774，0.3990）c=（0.3990，0.5774）,so the normalized matrix Nijis depicted as below.

Step 4.According to the normalized matrix Nij（i=1，2，…，m，j=1，2，…，n）and at tribute's weights wj（j=1，2，…，n）,the weighted normalized matrix WNij，i=1，2，…，m，j=1，2，…，n can be computed as below(take the WN11for example)

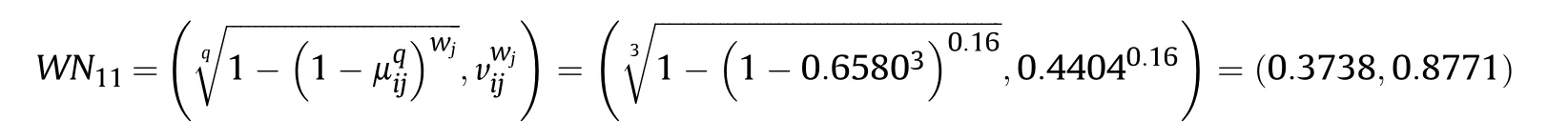
Then,we can derive other computing results,thus,all the results are list in WNijas below.

Then,we can derive other computing results,thus,all the results are list in Table 1.

Then,we can derive other computing results,thus,all the results

Step5.Compute the values of BAA and the BAA matrix G=［gj］1×ncan be constructed as follow s.(take the g1for example)are list as below.

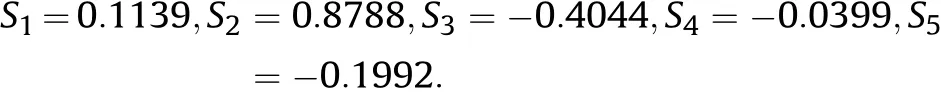
On account of the comprehensive evaluation result Si,the order of all alternatives can be derived,clearly,the bigger the

Then,we can derive other computing results,thus,all the results are list as below.

Step 6.Compute the distance D=［dij］m×nbetween alternatives and the BAA by Eq,(21).(take the d11for example)

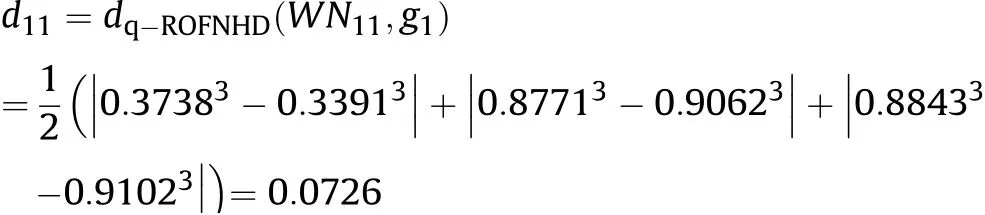
Table 1 The distances dij between alternatives and BAA.Step 7.Sum the values of each alternative's dij by Eq.(22).(take the S1 for example)=0.0726+0.0243+（-0.0325）+0.0495

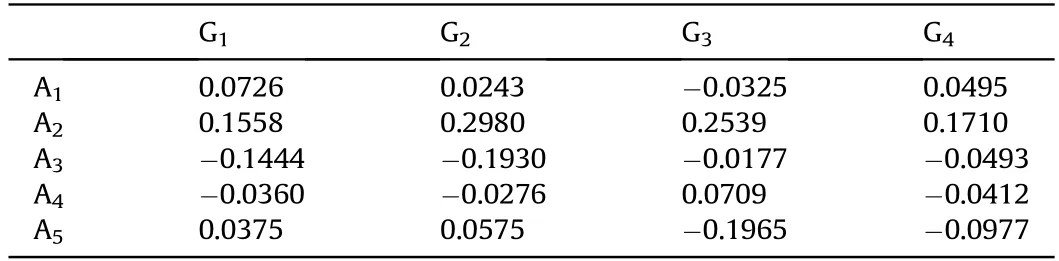
Table 1 The distances dij between alternatives and BAA.Step 7.Sum the values of each alternative's dij by Eq.(22).(take the S1 for example)=0.0726+0.0243+（-0.0325）+0.0495

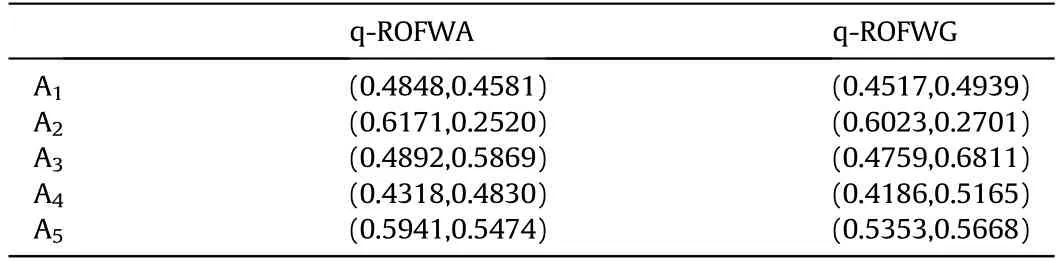
Table 2 The fused values by using some q-ROFNs aggregation operator.

Table 3 Score results of.Ai

Table 4 Comparative analysis results.

Since the S（WN11）＞S（g1）,comprehensive evaluation result Si,the better the choice.Obviously,the order is list as:A2＞A1＞A4＞A5＞A3and A2is the ideal solution.

6.2.Compare q-ROFNs MABAC method with some q-ROFNs operators

In this chapter,we compare our proposed q-rung orthopair fuzzy MABAC method with the q-ROFWA operator and the q-ROFWG operator.Based on the at tribute's weight and results of R,the fused values by the two aggregation operators are list in Table 2.

Compare the results of the q-rung orthopair fuzzy MABAC model with the two aggregation operators,The sorting results are slightly different in the ordering of alternatives,and the best alternatives are the same.How ever,q-rung orthopair fuzzy MABAC model has the precious characteristics of computing the distance between each alternatives and the bored approximation area(BAA)and can be applied to MADM problems more accurately and effectively.

7.Conclusion

In this article,we introduce the q-rung orthopair fuzzy MABAC model on account of the conventional MABAC model and some fundamental theories of q-rung orthopair fuzzy set.Firstly,we briefly review the theories related to the q-rung orthopair fuzzy sets(q-ROFSs)and introduce the score function,accuracy function,operation law s and some aggregation operators of q-ROFNs.Then,the computing steps of conventional MABAC model are briefly presented.Furthermore,combine the conventional MABAC model with q-ROFNs,the q-rung orthopair fuzzy MABAC model is constructed and the decision making steps are given in detail.the newly developed MABAC model is more accuracy and reasonable to deal with MADM for it can compute the distance between each alternative and the BAA.In the end,an actual decision making application for safety assessment of construction project has been given t has been given to testify this new model and some comparisons between this novel MABAC model and two q-ROFNs aggregation operators are provided to further demonstrate the merits of the q-rung orthopair fuzzy MABAC model.Clearly,our developed model has the advantage of depicting more fuzzy information and can derive stable computing results.How ever,because the q-ROFS and MABAC have limited practical applications,it may be difficult to gain acceptance in real MADM problems.In the future,the q-rung orthopair fuzzy MABAC model can be extended to apply to the risk assessment[73,74],many other ambiguous environments[75-78]and other application domains[79-82].

Acknowledgment

The work was supported by the National Natural Science Foundation of China under Grant No.71571128 and the Humanities and Social Sciences Foundation of Ministry of Education of the People's Republic of China(No.14XJCZH002,15YJCZH138).