Estimating the metal acceleration ability of high explosives

Dany Frem

Frem Co.,Beirut,Lebanon

Keywords:Gurney velocity High explosives Aluminized explosives Combined effects explosives Fragmentation warheads

ABSTRACT The Gurney method is widely used in the conceptual design stage of explosive fragmentation warheads employed in various weapons systems.This method states that the peak fragment velocity（V0）is a function of the Gurney velocity()and the charge-to-metal weight ratio(C/M).The current study is concerned with finding a practical approach for computing the Gurney velocity of pure and mixed high explosives which will eventually help warhead designers to select the best explosive to fulfill the needs of a particular mission.Using multiple regression analysis technique,a four-variable model was derived and used thereafter to estimate the Gurney velocity of aluminized and non-aluminized explosive formulations.The results show that the new model is particularly accurate in predicting the Gurney velocity of combined effects explosives,which are relatively a new class of high blast,high metal acceleration capability explosive compositions.©2020 China Ordnance Society.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.This is an open access article under the CCBY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1.Introduction

High explosives are an essential part of many types of ammunition used to engage and defeat air,sea and land targets.The damage inflicted on a given target is the result of blast and fragmentation generated following the detonation of the high explosive filler contained within a metal casing.Fragmentation warheads,in particular,can be classified into three categories,namely,natural fragmentation,controlled fragmentation and preformed fragments[1].In the latter two types of warheads,fragments of particular shape,mass and number can be obtained by introducing stress raisers such as grooves on the inside surface of the casing,or by embedding fragments of different geometries(e.g.cubes,spheres,rods,etc…)between the explosive charge and the metal casing.Natural fragmentation warheads,on the other hand,are know n to produce fragments exhibiting a wide range of size and shape of poor lethality which is due,in part,to the fact that nonoptimized irregular shaped-fragments tend to experience high aerodynamic drag forces when flying through the air,resulting in considerable velocity loss[2].The fragments velocity at a given distance from the warhead can be expressed using the following exponential form[3]:

where Vf(m/s)is the fragment velocity at distance x(m)from the point of detonation,k is the velocity decay constant,ρa(kg/m3)is the air density,m(kg)is fragment mass,S(m2)is the presented area of the fragment and Cdis the drag coefficient,its value depends on both the shape and velocity of the fragment.During WWII,R.W.Gurney came up with an original method to estimate the peak fragment velocity（V0/（km/s））ejected from shells and grenades[4].Gurney's method presumes that for any metal/explosive system the initial potential chemical energy of the explosive is partitioned between the kinetic energy of the fragments and the detonation products cloud.In deriving his model,Gurney has made some assumptions that the explosion gases are of uniform density and that the radial velocity（V）of the detonation gases varies linearly from the axis of symmetry of the explosive to the interface with the metal.How ever,despite these gross assumptions the Gurney model can be successfully applied to a wide range of charge-to metal weight ratio(C/M)and various warhead geometries.The expressions for spherical and cylindrical warheads are shown below:

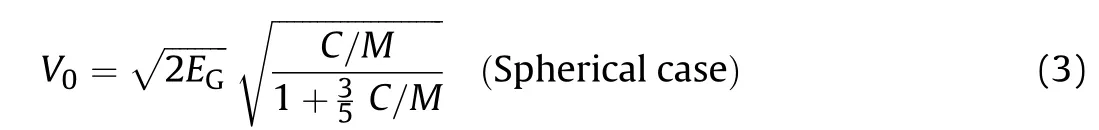
The value of Gurney velocity)for military and commercial high explosives is routinely obtained using the cylinder expansion test.The standard cylinder test consists of an explosive fitted inside a right circular cylinder 11.8-inch long,1-inch internal diameter and 0.1-inch thick wall[5].The cylinder is made of oxygen-free high conductivity(OFHC)copper(ρCu=8.94 g/cm3)to reduce spalling.A plane-wave lens generator or a suitable detonator/booster assembly is used to end-initiate the explosive.The wall radial motion is studied using a streak camera or other techniques such as the Velocity Interferometer System for Any Reflector(VISAR)[6]or the Photonic Doppler Velocimetry(PDV)[7]capable of directly measuring the wall velocity.For the 1-inch cylinder test,the wall velocities commonly reported in the literature are those measured at 6 mm and 19 mm wall displacement distances.This stems from the fact that,for head-on and side-on(grazing)detonation,all energy transfer to an adjacent metal is realized by the time the explosion products have reached an expansion volume of V≈2 and V≈7,respectively[8].These expansions correspond to displacement distances of 6 mm and 19 mm in the cylinder test.The 19 mm radial expansion value corresponds to the maximum or terminal wall velocity from which the(for the test explosive can be obtained by applying Gurney's cylinder equation Eq.(2).The high cost of the cylinder test hinders its use to evaluate the available large number of explosive formulations;hence it became necessary to develop alternative means by which the metal pushing ability of high explosives can be easily and rapidly accessed.There have been many equations published by several investigators[9-19,33,34],which provides a practical mean to estimate the Gurney velocity of CHNO-based explosives,although some of these methods can give relatively large deviations from experiment when applied to CHNOAl-based explosives.As a result,the present study aims to develop a simple model capable of accurately predictingfor aluminized and non-aluminized high explosive formulations.

2.Result and discussion

2.1.Developing the multivariate model

The new method should provide a reduced computational effort to facilitate the fast screening of energetic materials.This requirement means that the derived model should include the minimum number of terms and the terms themselves need to be easily calculable from available data.The first and most obvious term to consider is the density(ρ),which is justified by the fact that all of the detonation performance parameters,including the Gurney velocity,depend on it.A limited number of studies have addressed the relationship between explosive properties and the heat of combustion.Linear correlations were found to exist between the detonation velocity(D)[20],the relative explosive strength[21]and the specific heat of combustion(ΔHoc)in(k J/g)for a number of nitramine-based plastic bonded explosives.Furthermore,the heat of combustion was successfully used to evaluate the TNT equivalency of explosives with respect to quasi-static pressure in confined volumes[22].These findings suggest that the heat of combustion may also be used to estimateThe experimental heat of combustion can be obtained by burning a small sample(usually 1-2 g)in a bomb calorimeter in the presence of excess of oxygen(O2)[23].The measured energy of combustion(ΔUc)in(k J/mol)is converted to（ΔHc）using follow ing expression:

where R is the gas constant 8.314.10-3(k J/mol·K),T(K)is the temperature and Δngis the change in the number of moles of gas for the reaction.For an explosive with the general formula CaHbNcOdAlethe theoretical combustion equation in the presence of oxygen can be represented as follow s:

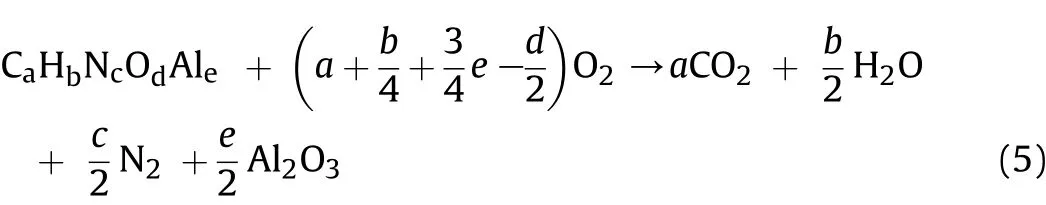
The combustion products CO2and N2are in the gaseous phase while H2O and Al2O3are in the liquid and solid phase,respectively.In this study,(ΔHoc)was calculated using the know n heat of formation（ΔHof）values of the products and reactants according to Eq.(6):

Multiple regression analysis was used to f i t experimentaldata using the density and the specific heat of combustion as variables.The data set includes pure and mixed explosives as well as aluminized and combined effects explosives.The goodness of the fit of the resultant two-variable model was ascertained from the coefficient of determination(R2=0.848)and the corresponding adjusted coefficient of determination(R2Adj=0.826),which represents the fraction of variation of the response explained and predicted by the obtained model[24].Subsequent studies and analysis have shown that the predictive power of the model can be significantly increased by including two more parameters,namely,(ζ)and(φ).The term(ζ)represents the total weight fraction of nitroaromatic explosives present in any composition.Moreover,if an aluminized formulation contains a nitroaromatic,then the weight fraction of the aluminum plus that of the nitroaromatic should be accounted for in the calculation of(ζ).The second term(φ),is merely a dummy parameter which can only have two values“0”and“1”.It is equal to“1”if the studied composition is a combined effects explosive;otherwise,it takes the value of“0”.

A four-variable expression for the estimation of the Gurney velocity is shown below:

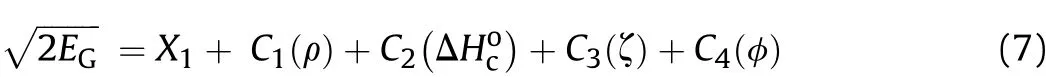
The intercept X1and the regression coefficients C1-C4were obtained from the multiple regression analysis and a data set made of seventeen experimentalshown in Table 1.The resultant final regression equation is as follows:

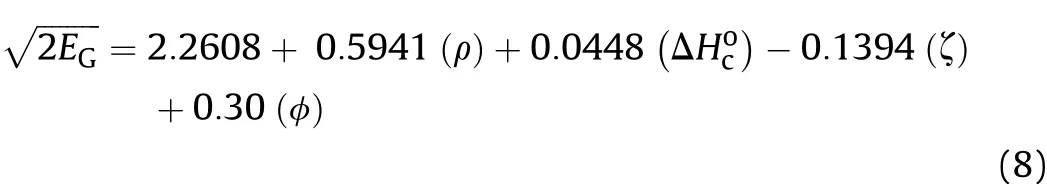
Multivariate results reported in Table 2 shows that all the independent variables are significant which is evident from P-values,which were all less than 0.05 for 95% confidence interval.Furthermore,inclusion of(ρ),(ΔHoc),(ζ)and(φ)variables explains 98.6%of the variability of the data.The small Significance of F(4.31×10-11)led to the rejection of the null hypothesis and confirms the validity of the regression output.

Table1 Experimental Gurney Velocities（As Compared to Those Calculated by Eq.(8).The Percentage Deviations are shown in Parenthesis.

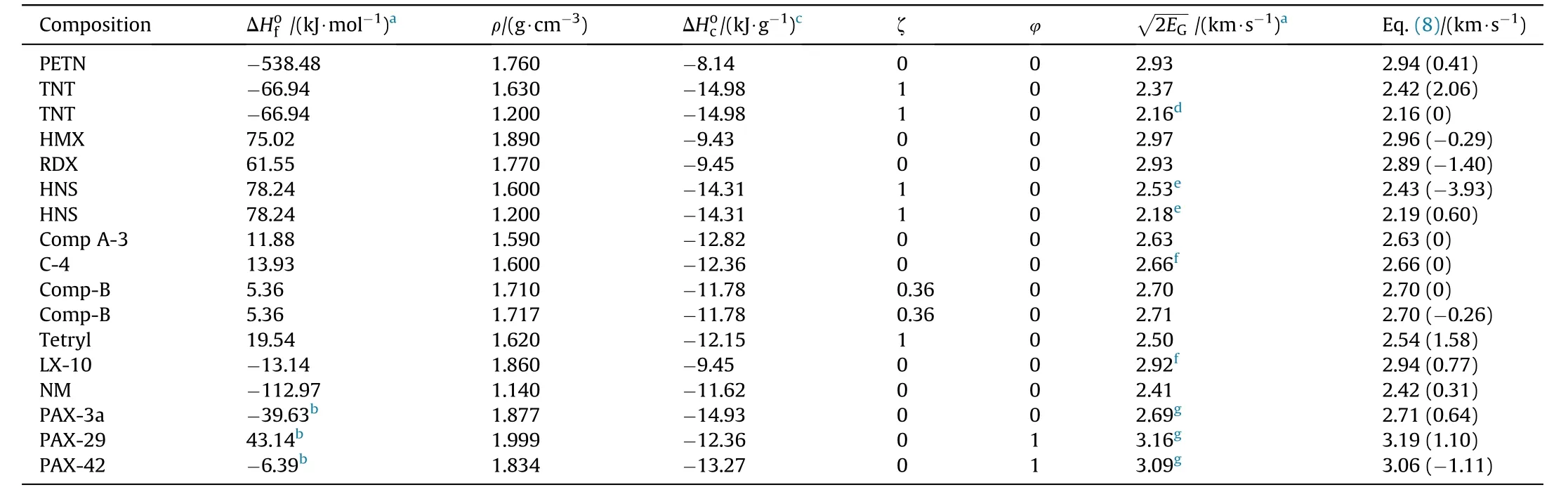
Table1 Experimental Gurney Velocities（As Compared to Those Calculated by Eq.(8).The Percentage Deviations are shown in Parenthesis.

b The heats of formation of Cellulose Acetate Butyrate(CAB)and CL-20 were taken from Ref.[26].aAll heats of formation(ΔHof)and Gurney velocities,unless otherwise noted,were taken from Ref.[25].c The heats of formation of CO2(g);H2O(l);HF(g)and Al2O3(s)were taken from Ref.[27].d Average value from two tests[28].e[29].f [30].g[31].

Table 2Results of multiple regression analysis(R2=0.986 and

Table 2Results of multiple regression analysis(R2=0.986 and

As can be seen in Table 1,most of the studied compositions are based on well-known families of explosives such as nitramines,nitroaromatics and nitrate esters.These formulations were carefully chosen so as to cover a wide range of loading densities(ρ=1.14-1.999 g/cm3)and Gurney velocities2.16-3.16 km/s).Furthermore,the computed specific heat of combustion(ΔHoc)according to Eq.(6)span a range from about-8 k J/g to-15 k J/g.The new method properly predicts theof conventional military explosives such as TNT,Comp-B and RDX,commonly used in munitions.The introduction of the variable（φ）into the model,on the other hand,allow s the accurate prediction(within±1%)of the Gurney velocities of combined effects explosives PAX-29 and PAX-42(row s 16-17,Table 1).These specific types of explosives have remarkable high blast energies and metal pushing capabilities compared to traditional aluminized explosives and high-energy plastic-bonded explosives.The poor metal acceleration ability of conventional aluminized explosives is consistent with the fact that little or no aluminum reacts during the early stages of detonation product expansion.This issue has been addressed by using specially formulated combined effects explosives capable of achieving high performance due to the early anaerobic reaction of aluminum with gaseous detonation products such as H2O and CO2to form Al2O3[32]with the release of substantial amounts of energy and,as such,combined effects explosives are potential candidates to be further developed for advanced blast and fragmentation warhead applications.Referring back to Table 1,it is observed that most of the Gurney velocities estimated using Eq.(8)are within few percent(1%-2%)of the actual measured experimental values.

2.2.Evaluating the predictive performance of current and existing methods for estimating

A test set made of nineteen explosive compositions was used to further evaluate the newly proposed model.The predictive performance of Eq.(8)was also compared to several predictive existing equations regarding their abilities in estimating the Gurney velocity of various aluminized and non-aluminized explosives.The relationships derived by Cooper[33]and Koch et al.[19]are widely used for the estimation of the Gurney velocity due to their very low mathematical complexity in that they only require the detonation velocity(D)as input as shown below:

Departing from the previous methods,Locking[34]arrived at a similar relationship,how ever,the constant in the denominator has been replaced by the term(fx)which is function of the explosive material:

where(ρ)is the density in kg/m3.In a recent paper[35],a method has been provided from which the Gurney velocity of aluminized and non-aluminized explosive formulations can be accurately obtained following Eq.(12):

where(PBKW)and(γBKW)are the detonation pressure and adiabatic coefficient calculated using the BKW thermochemical code.The empirical correlation proposed by Keshavarz[9]is used here to exclusively estimateof non-aluminized explosives:

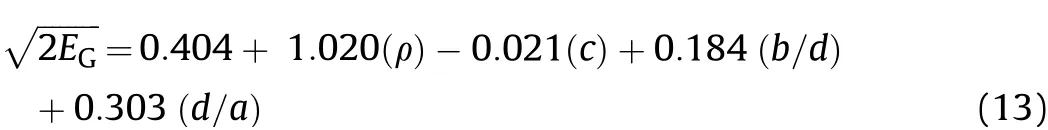
where a，b，c and d are the number of carbon(C),hydrogen(H),nitrogen(N)and oxygen(O)atoms.Eq.(13)offers the advantage of being simple and requires as input the density and the stoichiometry of the explosive.Obviously,in order to use Eq.(9)-Eq.(12)the detonation performance need to be calculated for all the compositions listed in Table 3.This has been carried out using the BKW code which is based on a chemical-equilibrium,steady-state model of detonation.The code computes the detonation properties using the Becker-Kistiakow sky-Wilson Equation of State(BKW-EOS)for the gaseous product and the Cow an EOS for solid explosion products[36].

The BKW-EOS is written as:

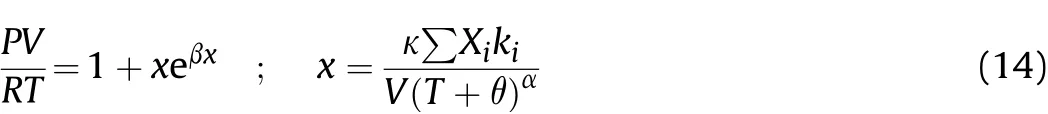
where(P),(V),(R),(T)and(x eβx)represent the pressure,molar volume of the gaseous products,gas constant,temperature and the imperfection term,respectively,while(Xi)and(ki)are the mole fraction and the co volume of each product species,respectively.(α),(β),(κ)and(θ)are empirical adjustable parameters.The RDX parameter set(α=0.50;β=0.16;κ=10.91;θ=400)was used to calculate the detonation pressures,adiabatic coefficients and most of the detonation velocities.Concurrently,the TNT parameter set(α=0.50;β=0.09585;κ=12.685;θ=400)was used to compute the detonation velocities for those explosives that generate too much solid carbon in the detonation products such as TACOT and PBX-9502(see Table 3).

The Root-mean-square deviation(RMSD)calculated using Eq.(15)was used as a measure of accuracy of prediction of Eq.(8)-Eq.(13):

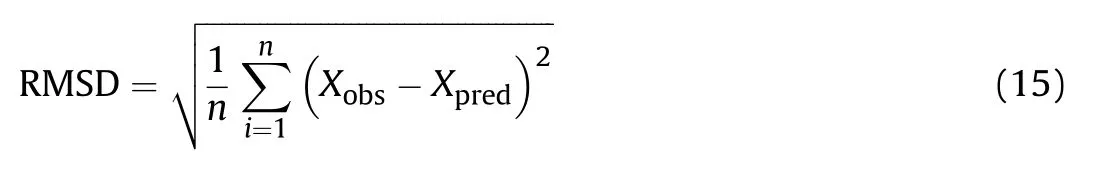
where(Xobs)and(Xpred)denotes the observed(or experimental)and the predicted values,respectively,while(n)is the number of observations.As seen in Table 4,Eq.(8)accurately estimates the Gurney velocities of non-aluminized explosives as 75%of the predicted values were within±1%of the observed values,indicating a good predictive performance.Chemical elements such as calcium(Ca)or phosphorus(P)present in minute amounts in some explosives(e.g.,HBX-1,H-6 and PBX-9404)were converted to their respective oxides(i.e.CaO and P4O10)and their heat contribution was considered in calculating the specific heat of combustion（ΔHoc）.Furthermore,halides,such as fluorine(F)and chlorine(Cl)were assumed to react with hydrogen to afford hydrogen fluoride(HF)and hydrogen chloride(HCl)as combustion products,respectively.Remarkably,all of the tested methods were found unsuitable to estimate the metal acceleration ability of reduced sensitivity explosives.For example,both Eq.(10)and Eq.(13)accurately predict the Gurney velocity for TACOT,but fail to do so for PBX-9502 which is also true for the rest of the equations.If the data for TACOT and PBX-9502 were excluded from the analysis,then Eq.(8)and Eq.(12)would have the best performance among the other equations with an RMSD of only 0.03 km/s.In addition,it is noteworthy to note that other investigators have reported similar findings in studying the energy delivered by a detonating explosive in the cylinder test[41].The model derived in Ref.[41]adequatelyreproduces the experimental cylinder energy at seven volumes expansion for relatively sensitive compositions containing(RDX)and(HMX),how ever,it overestimates by about 15%the cylinder energy for insensitive explosives such as nitroguanidine(NQ)and 1,3,5-triamino-2,4,6-trinitrobenzene(TATB).It also seems like many of the insensitive explosives share the characteristic of having low to moderate metal acceleration ability,which puts into question their use in high performance fragmentation weapons.On the other hand,predictions made by Eqs.(9)-(12)grossly underestimate the Gurney velocities of combined effects explosives(PAX-29n and PAX-30),some by as much as 12%.Besides,these results clearly indicate that factors other than detonation performance can also influence the Gurney velocity.For instance,the Gurney velocity of PAX-30 is 8.5%greater than that of Octol 75/25,even though both explosives have almost the same detonation pressure and velocity(see Table 3).In order to shed some light on the factors that may promote the early anaerobic aluminum oxidation,Anderson et al.[42]performed detonation calorimetry experiments and CHEETAH 5.0 thermochemical code calculations on a series of HMX-based aluminized formulations with varying compositions of HMX,aluminum,and binder materials.The results have shown that the binder type(energetic vs inert)was the sole most important factor in promoting aluminum reaction.Cylinder test wall velocity measurements for PAX-29,PAX-30 and PAX-42 also reveal that the aluminum particle size plays a crucial role in the onset of aluminum oxidation.In the case of formulations incorporating large aluminum particles(≥50μm),little or no reaction occurs even at large expansion volumes[43].Furthermore,the extent of aluminum reaction was affected by the available explosive percentages[32].Any potential user of Eq.(8)can identify a combined effects explosives(φ=1)if all of the following conditions are fulfilled:a)the presence of an“energetic”binder(e.g.,cellulose acetate butyrate plasticized with BDNPA/F);b)the use of small aluminum particles(＜50μm);and c)the presence of significant amounts(＞75 w t%)of an explosive material.If any one of these conditions is not met,then the explosive is classified as a traditional explosive and its(φ）value should be equal to zero(e.g.,PAX-3a,HTA-3,HBX-1).Lastly,referring to Table 4,It can be clearly seen that,Eq.(8)has the low est RMSD(0.05 km/s)compared to other equations which ranged from 0.13 km/s to 0.23 km/s.These results,supports the reliability of the model proposed to predict the Gurney velocity of various explosive materials.

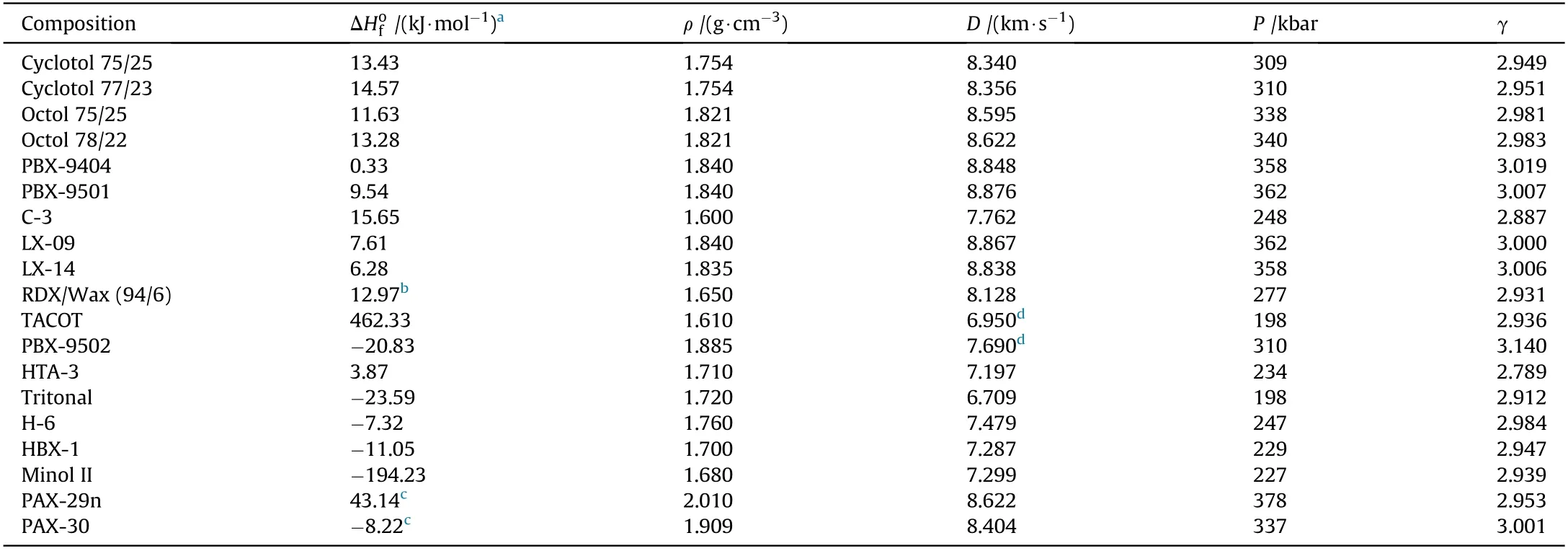
Table 3 Detonation performance calculated using the BKW thermochemical code.

Table4 Experimental Gurney VelocitiesAs Compared to Those Calculated by Eq.(8)-Eq.(13).The Percentage Deviations are shown in Parenthesis.

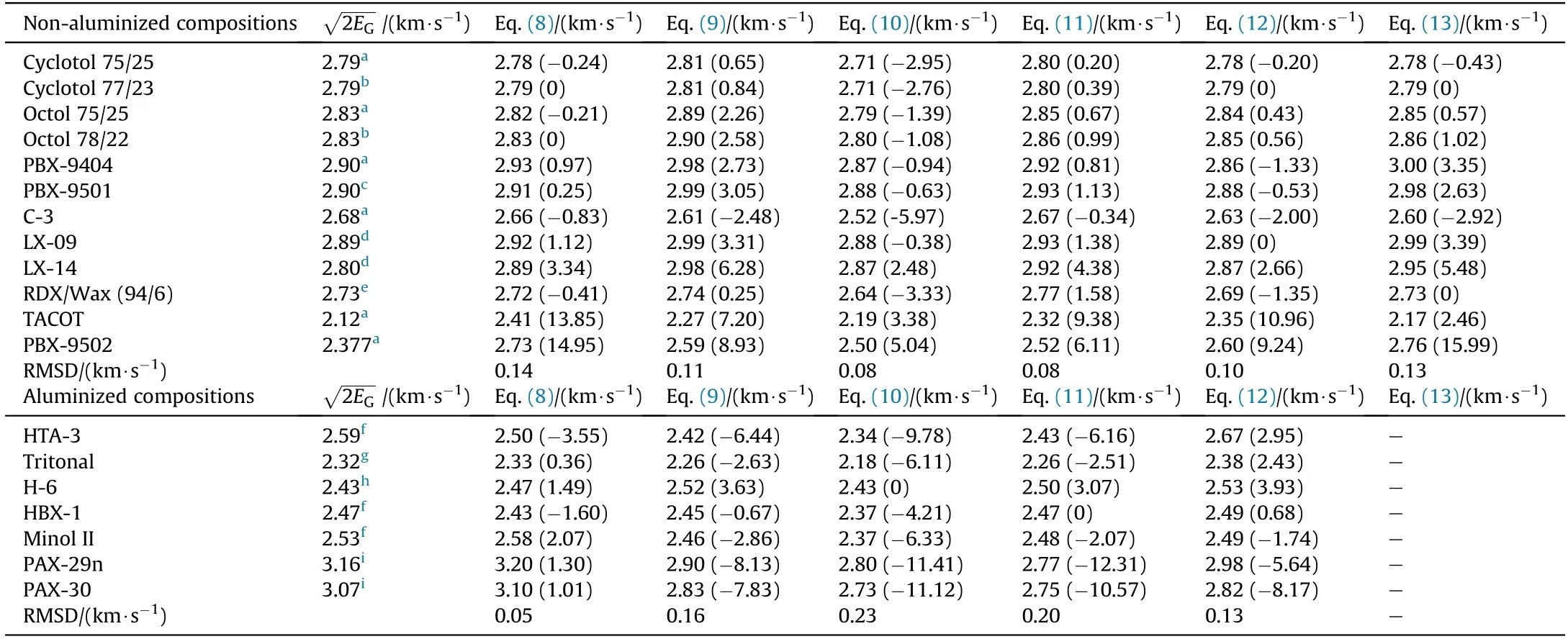
Table4 Experimental Gurney VelocitiesAs Compared to Those Calculated by Eq.(8)-Eq.(13).The Percentage Deviations are shown in Parenthesis.

Note:The heats of formation of CO2(g);H2O(l);HCl(g);HF(g)CaO(s);P4O10(s)and Al2O3(s)used in the calculation of（ΔH oc）were taken from Ref.[27].a[25].b[38].c[30].d[29].e[39].f[40].g[33].h[25,30].i[31].

3.Conclusions

Based on w hat has been discussed above,several conclusions can be draw n as follow s:

1 Multiple regression analysis was used to derive Eq.(8)for predicting the metal acceleration ability of condensed high explosives.

2 The optimized four-variable model is capable of accurately estimating the Gurney velocity of aluminized and nonaluminized explosives including combined effects explosives.

3 Eq.(9)-Eq.(12)were found to be unsuitable to estimateof combined effects explosives in that they all result in underestimating the Gurney velocity of such explosives.

4 Future studies should focus on providing a model for accurate estimation of the Gurney velocity of insensitive explosives.

List of chemical and atomic com positions of explosive com pound s/form ulations appearing in Tables 1,3 and 4

C-3:77/4/10/5/1/3 RDX/TNT/Dinitrotoluene/Mononitrotoluene/Ni

trocellulose/Tetryl

(C1.90H2.83N2.34O2.60)

C-4: 91/5.3/2.1/1.6 RDX/Di (2-ethylhexyl) sebacate/Polyisobutylene/Motor oil

(C1.82H3.54N2.46O2.51)

Comp A-3:91/9 RDX/WAX(C1.87H3.74N2.46O2.46)

Comp-B:63/36/1 RDX/TNT/Wax(C2.03H2.64N2.18O2.67)

Cyclotol 75/25:RDX/TNT(C1.78H2.58N2.36O2.69)

Cyclotol 77/23:RDX/TNT(C1.750H2.588N2.385O2.689)

HNS:2,2′,4,4′,6,6′-Hexanitrostilbene(C14H6N6O12)

H-6: 45/30/20/5/0.5 RDX/TNT/Al/D-2 Wax/CaCl2(C1.89H2.59N1.61O2.01Al0.74Ca0.005Cl0.009)

HBX-1: 40/38/17/5/0.5 RDX/TNT/Al/D-2 Wax/CaCl2(C2.06H2.62N1.57O2.07Al0.63Ca0.005Cl0.009)

HMX:1,3,5,7-Tetranitro-1,3,5,7-tetraazacyclooctane(C4H8N8O8)

HTA-3:49/29/22 HMX/TNT/Al(C1.556H1.963N1.708O2.091Al0.815)

LX-09:93/4.6/2.4 HMX/DNPA/FEFO(C1.43H2.74N2.59O2.72F0.02)

LX-10:95/5 HMX/Viton A(C1.41H2.66N2.57O2.57F0.16)

LX-14:95.5/4.5 HMX/Estane 5702-F1(C1.52H2.92N2.59O2.66)

Minol II:40/40/20 AN/TNT/Al(C1.233H2.880N1.528O2.556Al0.741)

NM:Nitromethane(CH3NO2)

Octol 75/25:HMX/TNT(C1.78H2.58N2.3602.69)

Octol 78/22:HMX/TNT(C1.732H2.593N2.39902.690)

PAX-3a: 64/9.5/20/6.5 HMX/BDNPA/F/Al/CAB(C1.384H2.572N1.849O2.183Al0.741)

PAX-29: 77/4.8/15/3.2 Cl-20/BDNPA/F/Al/CAB(C1.313H1.474N2.169O2.336Al0.556)

PAX-29n: 77/4.8/15/3.2 Cl-20/BDNPA/F/submicron-Al/CAB(C1.313H1.474N2.169O2.336Al0.556)

PAX-30: 77/4.8/15/3.2 HMX/BDNPA/F/Al/CAB(C1.299H2.501N2.141O2.308Al0.556)

PAX-42: 77/4.8/15/3.2 RDX/BDNPA/F/Al/CAB(C1.299H2.501N2.141O2.308Al0.556)

PETN:Pentaerythritol tetranitrate(C5H8N4O12)

PBX-9404: 94/3/3 HMX/Nitrocellulose/Tris-β-Chloroethyl phosphate

(C1.40H2.75N2.57O2.69Cl0.03P0.01)

PBX-9501: 95/2.5/2.5 HMX/Estane/BDNPA-F(C1.47H2.86N2.60O2.69)

PBX-9502:95/5 TATB/Kel-F 800(C2.30H2.23N2.21O2.21Cl0.038F0.13)

RDX:1,3,5-Trinitro-1,3,5-triazacyclohexane(C3H6N6O6)

TACOT: 2,4,8,10-Tetranitro-5H-benzotriazolo [2,1-a]-benzotriazol-6-ium,hydroxide,

inner salt(C12H4N8O8)

Tetryl:2,4,6-Trinitrophenyl-N-methylnitramine(C7H5N5O8)

TNT:2,4,6-Trinitrotoluene(C7H5N3O6)

Tritonal:80/20 TNT/Al(C2.467H1.762N1.057O2.115Al0.741)

94/6 RDX/Wax:(C1.70H3.39N2.54O2.54)