Numerical simulation of the blast wave of a multilayer composite charge

Xio-wen Hong ,Wei-ing Li ,*,Wei Cheng ,Wen-in Li ,He-yng Xu

a ZNDY of Ministerial Key Laboratory,Nanjing University of Science and Technology,Nanjing,PR China

b Chongqing Hongyu Precision Industrial Co.,Ltd,Chongqing,PR China

Keywords:Structure of composite charge Initiation mode Blast wave Cell size in calculation Numerical simulation

ABSTRACT The numerical simulation of a blast wave of a multilayer composite charge is investigated.A calculation model of the near-field explosion and far-field propagation of the shock wave of a composite charge is established using the AUTODYN finite element program.Results of the near-field and far-field calculations of the shock wave respectively converge at cell sizes of 0.25-0.5 cm and 1-3 cm.The Euler--fluxcorrected transport solver is found to be suitable for the far-field calculation after mapping.A numerical simulation is conducted to study the formation,propagation,and interaction of the shock wave of the composite charge for different initiation modes.It is found that the initiation mode obviously affects the shock-wave waveform and pressure distribution of the composite charge.Additionally,it is found that the area of the overpressure distribution is greatest for internal and external simultaneous initiation,and the peak pressure of the shock wave exponentially decays,fitting the calculation formula of the peak overpressure attenuation under different initiation modes,which is obtained and verified by experiment.The difference between numerical and experimental results is less than 10%,and the peak overpressure of both internal and external initiation is 56.12%higher than that of central single-point initiation.©2020 China Ordnance Society.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1.Introduction

Requirements for the damage of a weapon system,especially the release of damage energy of a warhead,have become precisely controlled with the development of efficient damage technology.The composite charge structure having inner and outer rings can be used to control the energy output of a warhead,realizing optional damage and multitask adaptability of the warhead[1-4].In 2012,the British company QinetiQ proposed a multilayer annular composite charge structure[5].The peak overpressure and quasi-static pressure were tested for two modes of the composite charge structure in a closed explosion chamber.Results show ed a difference in the energy output of the mode for different stages of initiation.Manfred Held[6]conducted an in-depth study on the detonation performance of dual inner and outer charges and analyzed the detonation characteristics of the dual charge,providing a theoretical basis for charge design.Kato et al.[7,8]studied a composite charge comprising high-density explosives with tungsten powder and high-detonation-velocity explosives.They found that the detonation velocity of the composite charge was improved and the burst pressure more than doubled comparing with a single-layer charge.

The blast wave is a kind of strong intermittent compression wave with high amplitude,short duration and strong destructive force.The damage effect depends mainly on the peak overpressure and positive pressure action time.For short-term pulse damage,it mainly depends on peak overpressure,while for long-term pulse damage,it mainly depends on the positive pressure action time,that is,the specific impulse,both of them reflect the energy output characteristics of the explosive.It is therefore important to study the law s that govern the shock wave of a multilayer composite charge for the design of the charge structure and evaluation of the energy of a high-efficiency damage warhead.There are numerous methods worth referencing for the numerical simulation of the shock wave of the explosion of a single-layer cylindrical charge.Mehdi Sotudeh Chiafi et al.[9],for example,demonstrated the use of the ALE method in a simulation of a blast wave in air.The interaction between the simulated fluid and structure,combined with an explosion test under three different working conditions,verified the rationality of the numerical simulation.The results demonstrated that the method can predict the interaction of the explosion and structure.Artero-Guerrero Jet al.[10]studied the effect of the shape of the charge on the shock wave generated.The multimaterial fluid-solid coupling algorithm (ALE method)compensated for the shortcomings of the CONWEP method,and the incident and reflected waves generated by different shapes of charge were obtained.Detailed analysis and verification results show that the dynamic effect of the reflected pressure impulse should always be considered in structural design.The front of the structure is the decisive factor of the impulse generated by the explosion.Bj¨orn Zakrisson et al.[11]simulated the dynamic response of a steel plate under near-field blast loading and compared it with experimental results.Convergence analysis using a finite element mesh was carried out by mapping results from two dimensions to three dimensions with a Euler algorithm.Results showed that the near-field explosion in air can be simulated by constructing a model of reasonable size.A.Langlet et al.[12]used the ALE method to simulate the propagation of a blast wave in air and its reflection from assumed rigid cylindrical obstacles and measured the pressure of the blast wave acting on a rigid cylinder.Simulations were conducted using the proposed model and method.A reliable prediction of the pressure time history recorded on a rigid cylinder was presented.T.Børvik et al.[13]investigated whether a pure Lagrange formulation can be applied to determine the structural response in a specified blast load problem or if more advanced approaches,such as the fully coupled Eulerian-Lagrange approach,are required to obtain reliable results.They numerically simulated the dynamic response of a 20-ft ISO container at a distance of 120 m under a 4000kg-TNT blast load using Euler,Lagrange,and ALE methods and carried out a full-scale test.However,there have been few numerical simulations of a multilayer composite charge.It is difficult to calculate the shock wave pressure using an empirical formula owing to the complexity of the shock wave field of the multilayer composite charge and different initiation modes affecting the shock wave field.It is therefore necessary to obtain the shock wave propagation process and attenuation law of the composite charge through numerical simulation;this will be helpful for further optimization of the design of the structure of the multilayer composite charge.

On the basis of the finite element program AUTODYN,the present paper investigates a numerical simulation method for the propagation of the blast wave of a multilayer composite charge under different initiation modes,establishes a calculation model of the near-field explosion and far-field propagation of a composite charge,and determines the cell size and solver before and after mapping.The formation,propagation,and interaction of the shock wave for the composite charge are numerically simulated using three initiation modes:central single-point initiation,external multi-point initiation,and internal and external simultaneous initiation.A test was carried out to verify the results.

2.Numerical modeling and parameter selection

2.1.Calculation model of the multilayer composite charge

The composite charge studied in this paper is mainly composed of three parts:the internal charge is 8701(RDX 95%,DNT 3%,CZ 2%)with a diameter of 35 mm,polyurethane with a thickness of 15 mm in the middle,and the RDX-aluminum-wax(RDX/Al/Wax 76/20/4)with a thickness of 15 mm in the outer,the entire length of the charge is 80 mm and the mass is 648 g.The critical detonation diameter of the RDX-aluminum-wax explosive was 20 mm,so the thickness of the aluminized explosive was designed to be less than 20 mm,so that the outer charge was not completely detonated when the center was detonated.To realize the controllable output of the charge energy,the center charges detonate for partial detonation of the multilayer composite charge whereas the internal and external charges simultaneously detonate for full detonation.

A three-dimensional(3D)model is established according to the structure of the multilayer composite charge,and three gauges are set at 0.5 m in the direction orthogonal to the orientation of the composite charge.The 3D model in AUTODYN comprises an air domain with dimensions of 1 m×0.5 m×0.5 m,while the cell size of the 3D model is 1 cm.Nonreflecting boundary conditions are set at the boundary of the air domain and the y=0 plane are imposed the axially symmetric boundary condition.The calculation model and top view are shown in Fig.1.

2.2.Material model and parameter selection

The response of a charge depends on the initiation mode,and internal and external charges should thus have different explosive model parameters set according to the initiation mode.When the center is detonated, the 8701 explosive obeys the Jones-Wilkins-Lee(JWL)equation of state(EOS)[14],while an ignition grow th reaction model is adopted for the aluminumcontaining explosive[15].In the case of external detonation,an ignition grow th reaction model is adopted for the 8701 explosive while the aluminum-containing explosives obey the JWL EOS[16].For internal and external simultaneous initiation,the 8701 and aluminum-containing explosives obey the JWL EOS,and the intermediate polyurethane layer is described by the shock EOS[17].Details of the explosive model and polyurethane parameters are given in Table 1-Table 4.

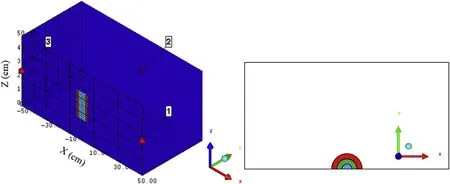
Fig.1.Calculation model and top view.

Table 1 Parameters of the explosive JWL EOS.

The energy release of the secondary reaction to the outer aluminum-containing explosive is described by the equation of the Miller reaction rate:

where G,a,and b are directly related to the reaction rate,and the reaction rate indices of aluminum-containing explosives are generally a=1/2 and b=1/6[18].G is related to the characteristics of the explosive and the particle size of the aluminum powder.The method of determining the model parameters refers to the literature[19].The parameters of the Miller energy release model determined by the iterative calculation is Q=6 GJ/m3,a=0.5,b=0.167,G=0.028.

The air is described by the ideal-gas EOS.The material parameters are taken from the AUTODYN material library.The initial specific internal energy of air is e0=2.068×105J/kg.

2.3.Calculation results and analysis

Because an axisymmetric model is adopted for the composite charge itself,the symmetry of the detonation input may affect the energy output after the detonation of the charge.In general,the initiation modes are multi-point initiations instead of ring initiations,and the effect of the number of initiation points needs to be considered for external multipoint initiation and simultaneous internal and external initiation.The effect of the number of initiation points on the overpressure is thus explained here.The study considers 3,4,5,6,8,and 12 initiation points and end-face detonation at the upper end of the composite charge.There are seven types of initiation mode,and the calculation model has Y-axis symmetry.The distribution of the initiation points on the end face for various initiation modes is shown in Fig.2.

Fig.3 is a diagram showing the state of development of blast w aves at the time of initiation at four points inside and outside(I b))and initiation at the end face(Ⅶb)).The figure reveals that when the four inner and outer points are detonated,the blast wave expands to 2.1-4.2 times of the diameter of the charge at 10μs.At this time,the high-pressure area generated by the respectiveinitiation points is axisymmetric.The high-pressure zone formed when the end face is detonated is both center-symmetric and axisymmetric.With the propagation and development of the blast waves,after 30μs and until the blast w aves propagate to the air boundary,a symmetric waveform forms at approximately 5 charge diameters,and the shock wave waveform and intensity of the detonation of the four inner and outer points and those of the endface detonation are approximately the same.

Table 4 EOS parameters of polyurethane.

Fig.4 is a comparison of the results of peak overpressure and relative deviation of shock wave of composite charge at different observation points under different initiation modes.It is seen that for both the internal and external simultaneous initiation or the external multi-point initiation mode,the number of initiation points has little effect on the peak overpressure of the blast wave at a diameter of 5 times the charge diameter.In terms of the effect of the mesh resolution in the numerical simulation,the maximum deviation is less than 7%.Therefore,to improve the calculation efficiency,the model can be approximated by simplifying the model for a two-dimensional(2D)axisymmetric problem to make the farfield calculation of the explosion in a large air domain.

3.2D calculation model and algorithm selection

3.1.Calculation model and far-field mapping

A 2D axisymmetric model is established to simplify the calculation.Owing to the high frequency of the near-field shock wave,narrow pulse width,fast attenuation,and high peak pressure,the mesh is divided sufficiently to accurately simulate the near-field shock wave,generally on the order of millimeters.In calculating the entire shock wave development of the composite charge in the near field and far field,the calculation efficiency is low if a mesh on the order for millimeters is adopted for the entire space having dimensions of 3 m×6 m.The remapping capability unique to AUTODYN is used to reduce the computational cost.All analyses are performed in two stages.In the first stage,the near-field shock wave simulation of the composite charge is carried out.The air domain is established using the Euler-Godunov solver of AUTODYN.The air domain has dimensions of 1 m×0.5 m and 200×100 cells.The explosive and explosion-proof material are set in the air domain.The calculation stops when the blast wave reaches the boundary and the remap file is saved.In the second stage,the far-field calculation model is established.The air domain hasdimensions of 3 m×6 m and 150×300 cells,with the cell size being 2 cm.The calculation result of the first stage is mapped to the far-field calculation model to further calculate the propagation of the blast wave.Fig.5 shows the near-field computing model and far-field computing model after mapping.A flow out boundary condition is assigned to the boundary plane of the air domain in both stages.

Table 2 Explosive unreacted JWL EOS parameters.

Table 3 EOS parameters of the reaction rate of the explosive ignition grow th model.

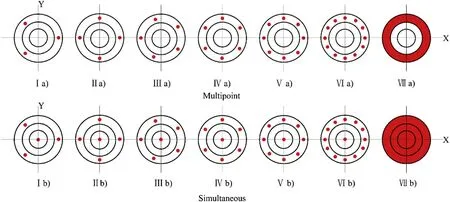
Fig.2.Distribution of the initiation points for different initiation modes.

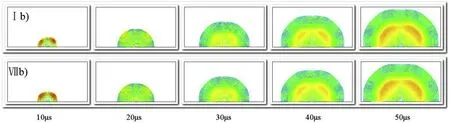
Fig.3.Development of the shock wave at the fourth point of internal and external initiation and end-face initiation.

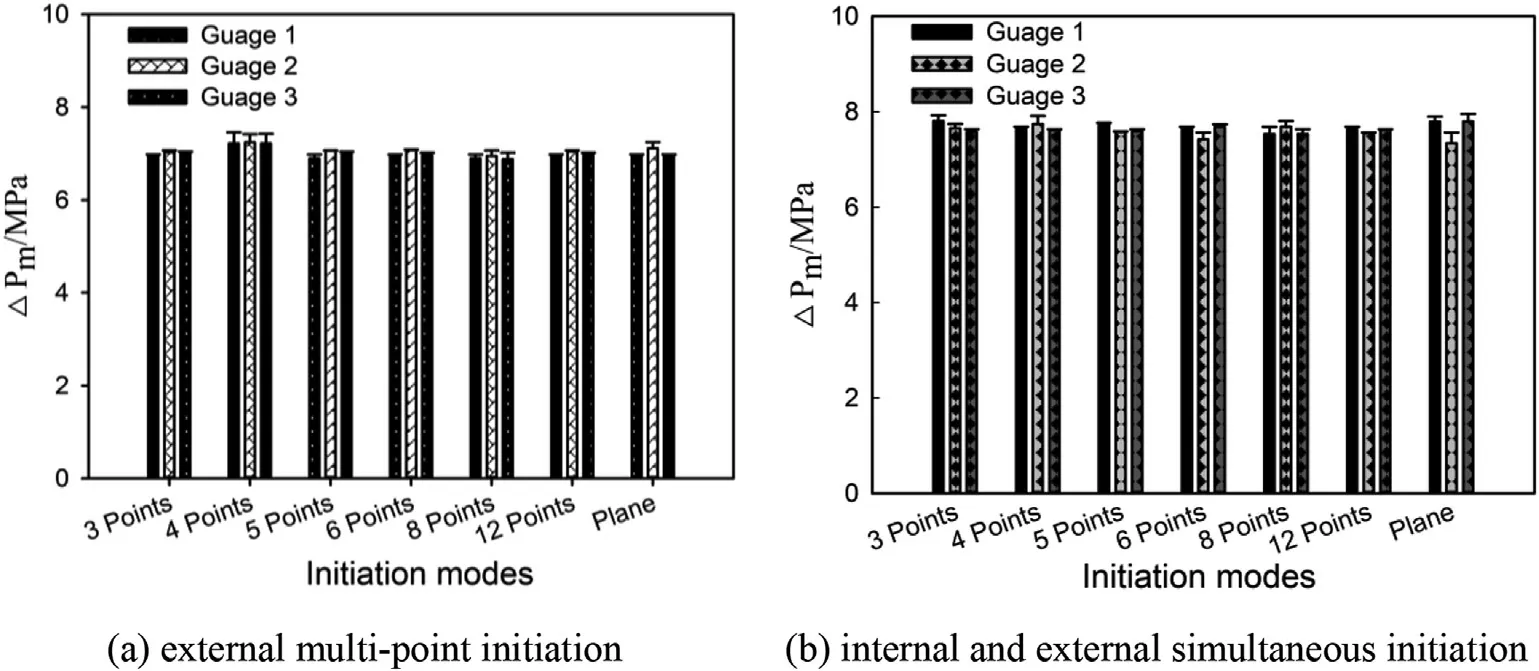
Fig.4.Comparison of the peak overpressure and deviation of the shock wave at each gauge point for different initiation modes.

The position of the initiation point is shown in Fig.5.For the comparison and analysis of overpressure at different scaled distances,six gauges are arranged equidistantly on the rigid ground.The positions of the mapping position(0 m,1.04 m)and gauges are shown in Fig.6.

Results need to be obtained before mapping using the Euler-Godunov solver,which is suitable for liquid,gas,and largely deformed materials.A material is transferred from one unit to another,which may contain many substances.The shock-wave field of the charge is calculated using the solver and then mapped to a larger spatial area.The Euler-Godunov solver and Euler-fluxcorrected transport(FCT)solver can be used to calculate the spatial region at this time.The Euler-FCT solver is usually used to solve the problem of strong discontinuity in physical model design(e.g.,the cases of propagation of the shock front and interface in space and the propagation of the blast wave in space)and highly precise results can be obtained.Different solvers are later used to compare and analyze the shock wave of the composite charge.

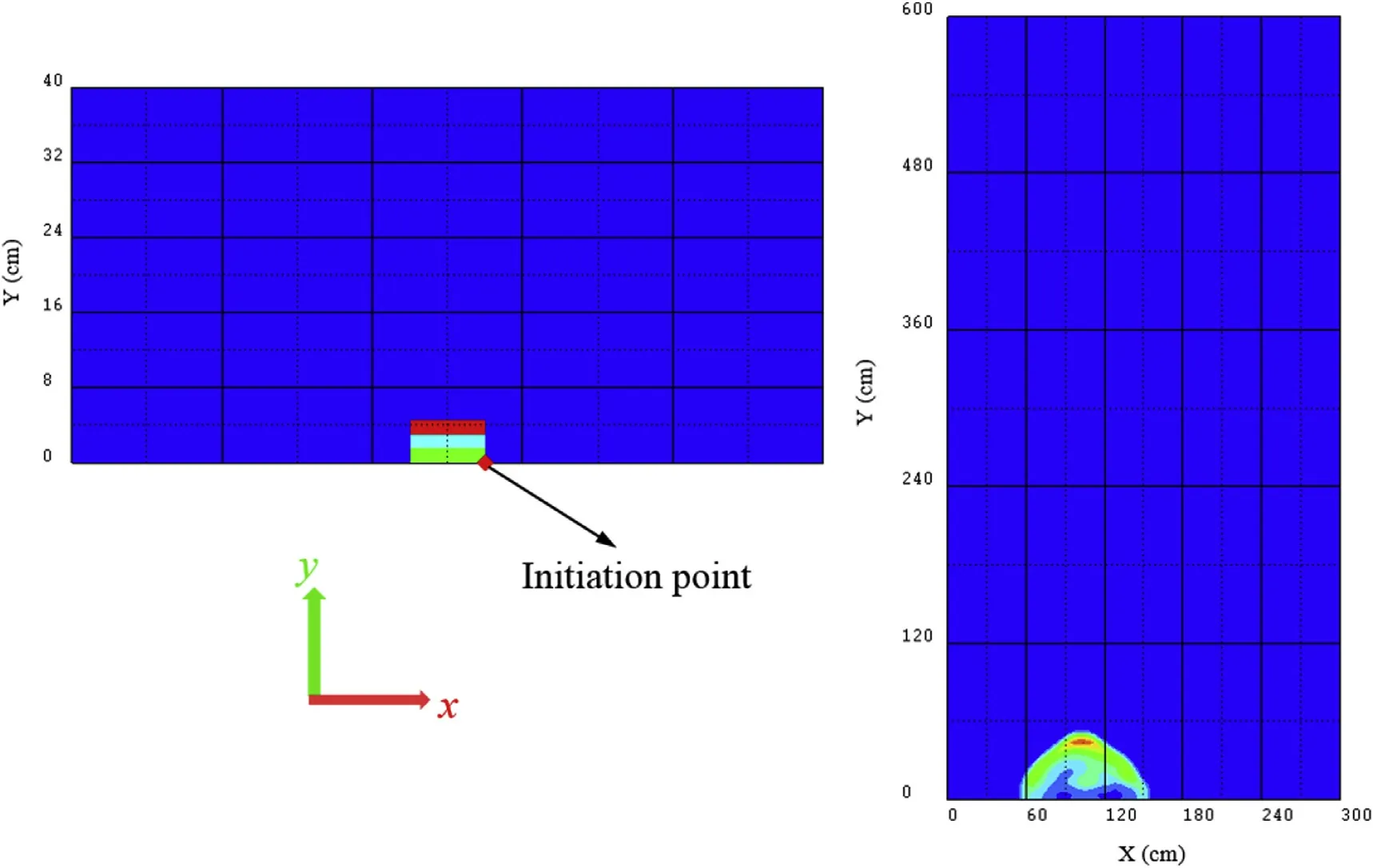
Fig.5.Near-field computing model and far-field computing model after mapping.

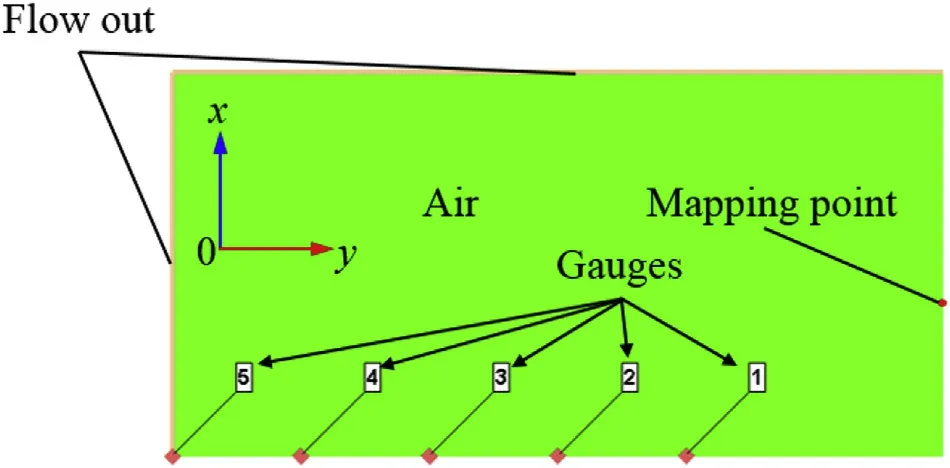
Fig.6.Locations of the mapping point and gauges.

Fig.7 is the time history curve of the shock-wave overpressure obtained using two types of solver at a scaled distance of 2.25 m/kg1/3.By comparing the curves,it is obvious that the peak overpressure calculated using the Euler-Godunov solver is lower than that calculated using the Euler-FCT solver,and the solution accuracy is not guaranteed.The Euler-Godunov solver is therefore suitable for modeling the blast wave but its accuracy is obviously insufficient for the problem of shock-wave propagation,which is consistent with the results of Borve et al.[20].Therefore,in this paper,Euler-FCT solver is used to simulate the mesh sensitivity.

3.2.Mesh sensitivity analysis

The convergence of the cell size should be analyzed before numerically simulating the blast wave.Rough meshing in the farfield region of the explosion can provide accurate results while using the same cell size in the near-field region of the explosion may provide inaccurate results.How ever,the use of a cells that are too small will reduce the calculation time step,which in turn reduces the calculation efficiency and increases the requirement of computer hardware.It is thus necessary to analyze the size effect of the cells.Because a two-step procedure is used in the numerical simulation,the mesh sensitivity is mainly analyzed for the premapping and post-mapping models.

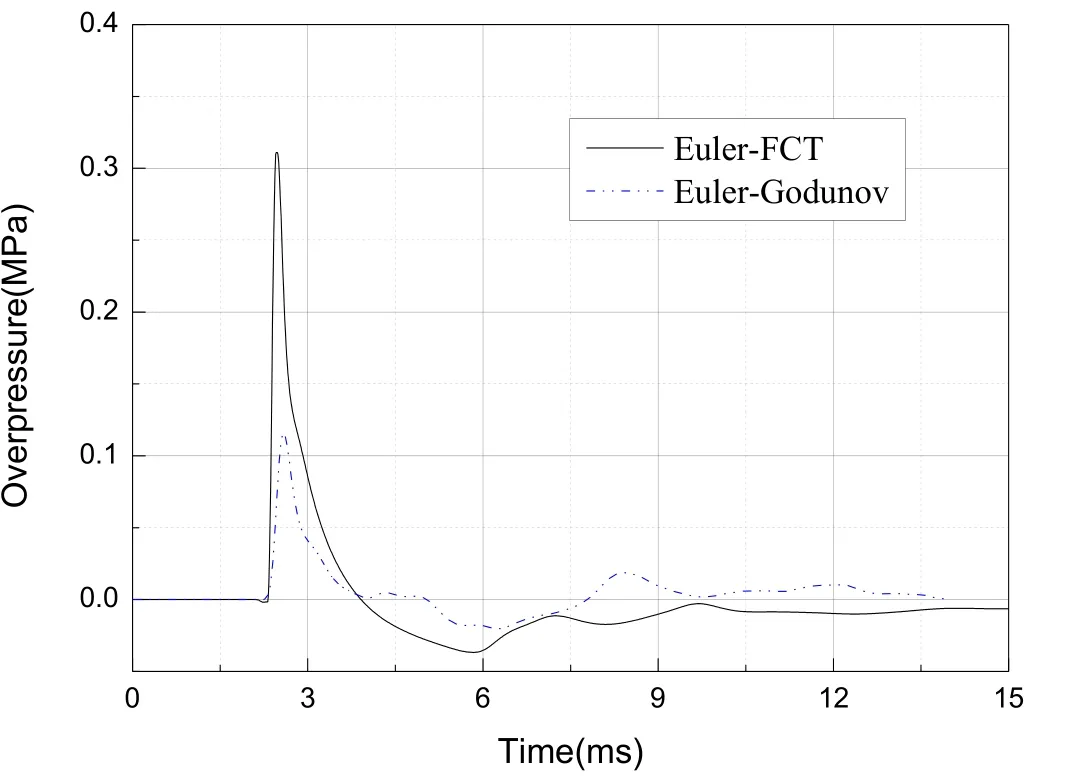
Fig.7.Comparison of time history curves of shock-wave overpressure at a scaled distance of 2.25 m/kg1/3 obtained using two solvers.

Adopting the computational model established in Section 3.1,the blast wave of composite charge in the near field is simulated using cell sizes of 0.25 cm,0.5 cm,0.6 cm,0.75 cm,and 1 cm.Fig.8 shows the difference in the near-field region.The time history curve of overpressure at a distance of 0.021 m/kg1/3is presented for different cell sizes.The figure reveals that with an increase in cell size,the waveform of the shock wave becomes divergent and seriously distorted,when the cell size becomes larger,the shock wave diffusion loss is larger,more time is needed for each cycle,which can be seen from the larger arrival time of the shock wave when the mesh size is larger[21].It is considered that the calculation is convergent in the cell size range of 0.25-0.5 cm.It can also be seen that two shock waves in the near field regime were obtained,this phenomenon is related to the characteristics of shock wave generated by cylindrical charge[22],the cylindrical charge can generate multiple shocks.Similar to the characteristics of shock wave of cylindrical charge,cylindrical composite charge also generates two or even three shocks.

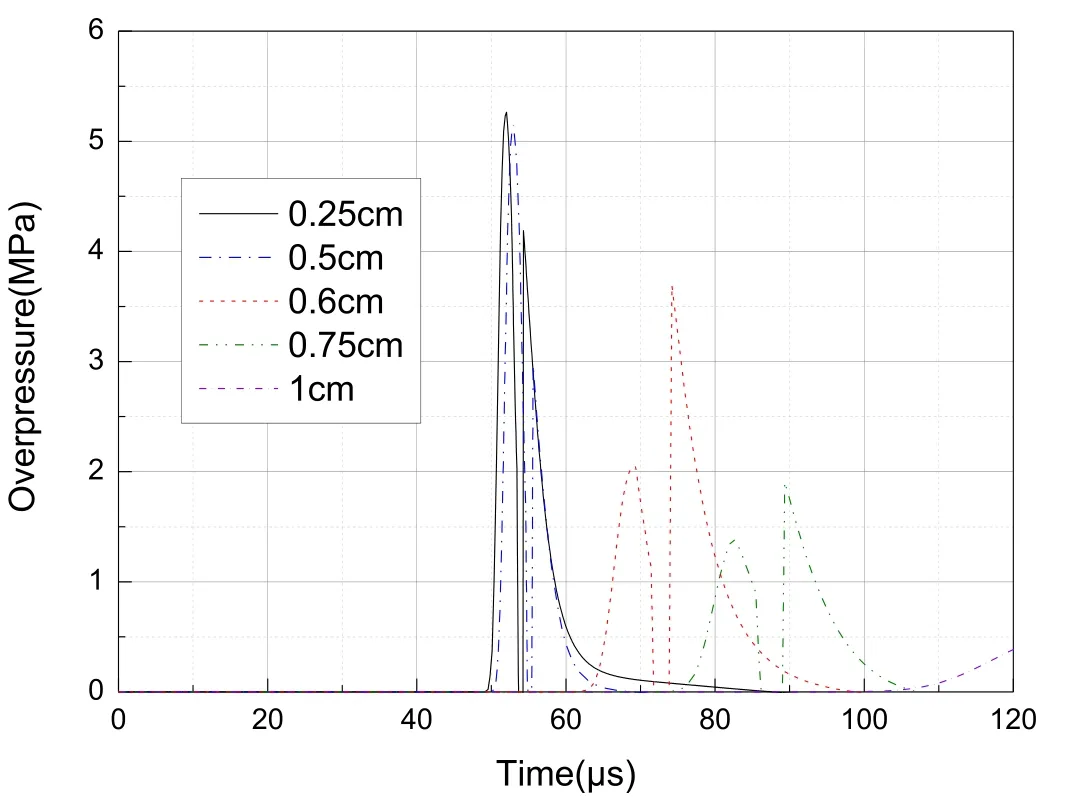
Fig.8.Comparison of overpressure time history curves in the near-field region for different cell sizes.

The blast wave of the composite charge in the far field is simulated using cell sizes of 1 cm,2 cm,2.5 cm,3 cm,4 cm,and 6 cm.The time history curves of overpressure at a scaled distance of 2.25 m/kg1/3in the far field are given for different cell sizes in Fig.9.It is seen that with an increase in cell size,the peak of the shock wave gradually changes from steep to gentle,and the wave front pressure increases.The slope of the force rising from zero to the peak decreases,and the waveform of the blast wave is slightly distorted.It is considered that the calculation is convergent in the cell size range of 1-3 cm.

From the point of view of the characteristic parameters of the shock wave,the sensitivities of the positive overpressure,positive impulse,and arrival time of the shock wave to the size of the cells is studied.According to the time history curves of overpressure in the far field for different cell sizes obtained by numerical simulation,the positive overpressure,positive impulse,and arrival time of the shock wave at different scaled distances are calculated.Fig.10 shows the comparison curves of the characteristic parameters at different proportions of distance for different cell sizes.It is observed that the positive impulse and arrival time of the shock wave almost coincide with each other,while the positive overpressure varies greatly at smaller proportions.The difference in cell size is large,indicating that the positive overpressure of the shock wave is more sensitive to the cell size while the positive impulse and arrival time of the shock wave front are less sensitive to the cell size.

4.Results and analysis of calculation

4.1.Process of detonation-wave propagation for different initiation modes

The shock wave propagation and variation patterns of composite charge are presented in Table 5 for different initiation modes and different times.The interaction of the incident wave with the ground-reflected wave forms an irregular reflection wave having a three-wave structure,the numerical simulation shows that the intersection points of incident wave,reflected wave and Mach wave are 1 m,1.2 m and 1.35 m away from the projection point of the detonation center respectively when the central single-point,the external multi-point and the internal and external simultaneous initiations occur,and the intersection of the incident wave,reflected wave,and Mach stem(i.e.,the triple point)grow s gradually with continued outward propagation of the shock wave.How ever,there are obvious differences in the waveform of the shock-wave pressure and in the form of the waveform relating to propagation characteristics of the detonation wave of the composite charge for different initiation modes and the reaction state of the charge.For central single-point initiation,an obliquely incident detonation wave enters the polyurethane material with a wave impedance less than that of the explosive.A shock wave is transmitted and a release wave reflected.The transmitted shock wave initiates the detonation of the outer charge to form a new shock wave that continues to propagate.For external detonation,a spherical wave forms at the detonation point of the outer charge,obliquely incident to the low-impedance explosion-proof layer.Shock waves converge at the inner charge to generate Mach overpressure and form a new shock wave front that propagates towards the bottom of the charge.When inside and outside charges are detonated at the same time,the spherical wave formed by the inner charge propagates from the end to the bottom of the charge.The detonation velocity of the inner charge is slightly higher than that of the outer charge.After the incident shock wave generated by the outer charge has traveled through the low-impedance explosion-proof material,the transmitted shock wave converges at the inner charge.An area of overpressure also forms,but the formation is relatively late owing to the effect of the sparse wave,which can be clearly seen from the comparison of shock wave pressure waveforms of multi-point initiation at 1000μs and 1500μs and simultaneous initiation inside and outside.

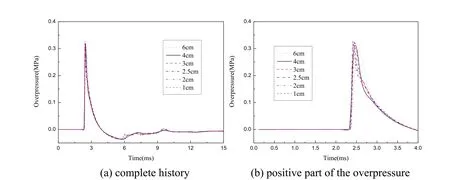
Fig.9.Comparison of curves of the overpressure time history in the far-field region for different cell sizes.

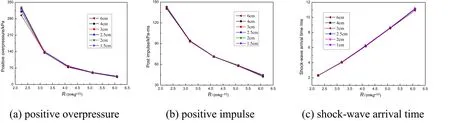
Fig.10.Curves of characteristic parameters of the shock wave against scaled distance for different cell sizes.

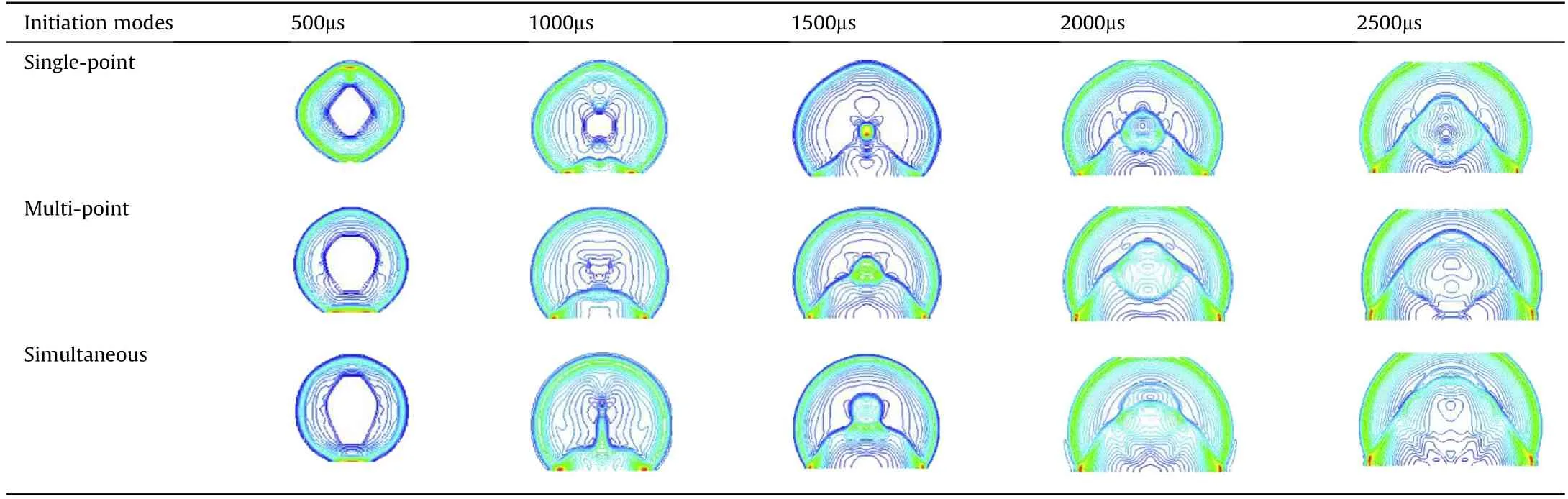
Table 5 Development and variation of shock-wave pressure waveforms for different initiation modes.

The internal wave propagation and action mechanism of detonation are also reflected in the shape of the macroscopic shockwave pressure waveform.Comparing the shock-wave pressure waveform at different times in Table 5 reveals whether the waveform is the superposition of the incident wave and reflection waves,the intersection of three w aves,or the waveform and pressure distribution in the zone of negative pressure after the shock wave.A difference in the initiation mode leads to a difference in the shockwave waveform and pressure distribution.To more intuitively show the effect of the initiation mode on the shock-wave pressure distribution at different times,a maximum overpressure distribution diagram is draw n for comparative analysis.Here,the case of external multi-point initiation is illustrated as an example.Other initiation modes produce similar results.The maximumover pressure distribution diagram for different initiation modes and the same time can then compared.

Fig.11 shows the maximum-overpressure distribution of composite charge at different times for external multi-point detonation(Ⅶa)).Fig.11 reveals that the area of the maximum-overpressure distribution of the shock wave increases with the propagation distance and action time of the shock wave(i.e.,the range of the area containing Mach action increases),the height of the Mach stem increases,and,as the action time increases,the distance between the maximum-overpressure distribution lines decreases owing to decreasing intensity of the shock wave.

Fig.12 compares the maximum-overpressure distribution of the composite charge for different initiation modes at 3 ms.It is clearly seen from the figure that the maximum-overpressure distribution is greatly affected by the initiation mode,and the area of the overpressure distribution area of central single-point initiation is smaller than that of internal and external simultaneous initiation and that of external multi-point initiation.This is because the energy release rate of composite charge is different under different initiation modes.When the central single-point initiation occurs,the reaction of the outer aluminized explosive is incomplete,and the energy of the explosive has not been fully released.When the external multi-point initiation and the simultaneous initiation occur,the overdriven detonation is formed in the composite charge,so the shock wave propagates faster and the distribution of peak pressure waveform is also different.

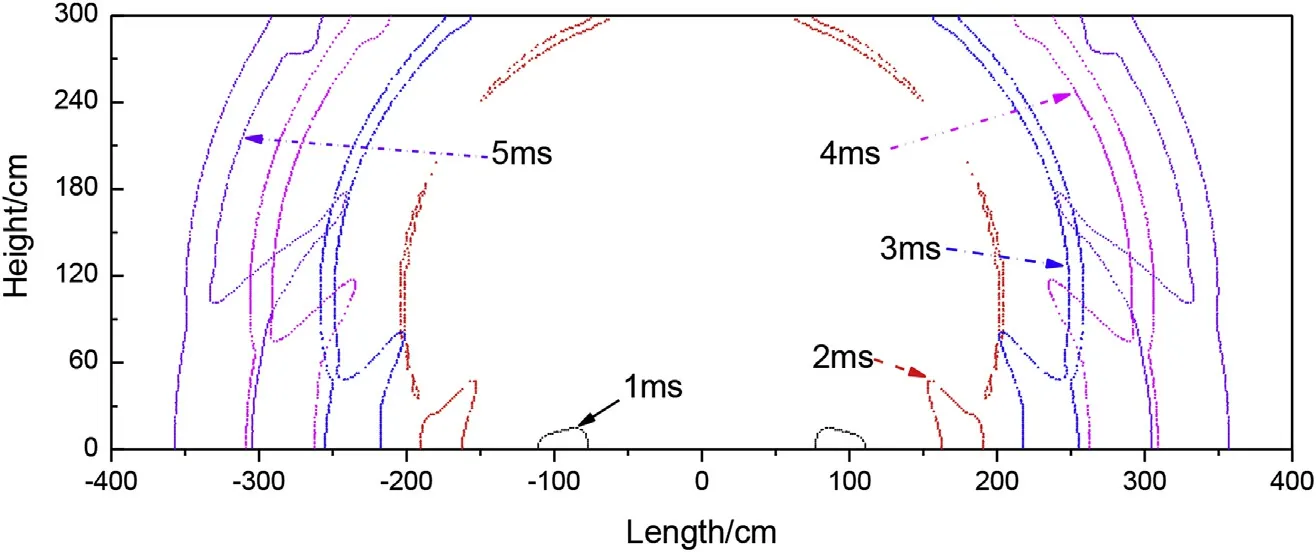
Fig.11.Maximum-overpressure distribution at different times for external multipoint initiation.

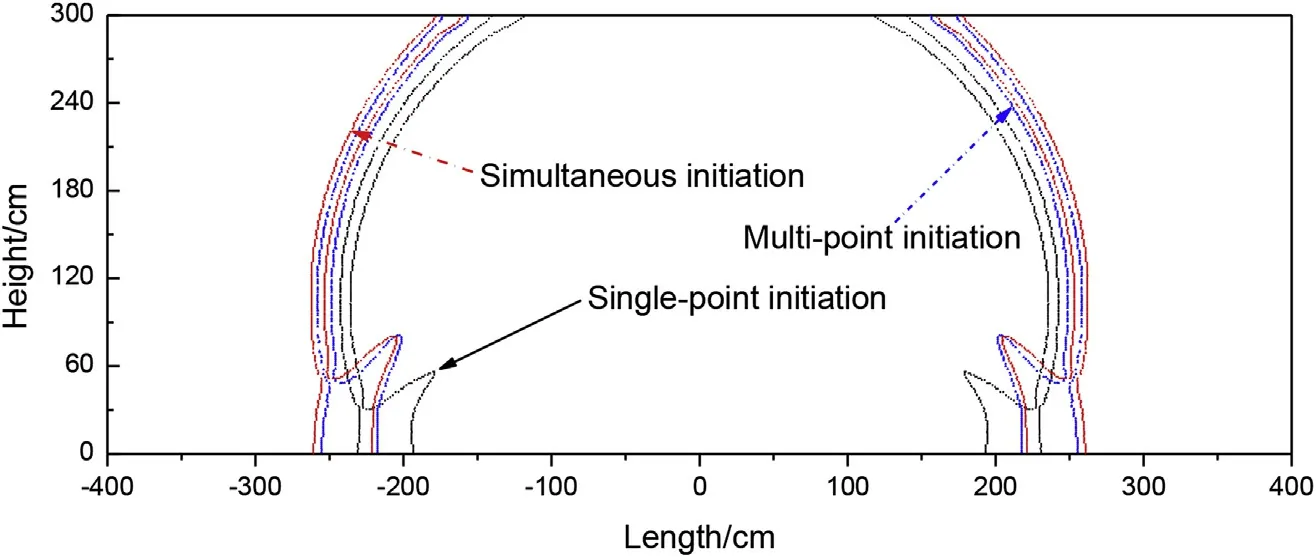
Fig.12.Maximum-overpressure distribution at 3 ms for different initiation modes.

4.2.Analysis of shock-wave pressure for a composite charge

The relationship between the peak overpressure and the scaled distance of the composite charge for different initiation modes can be characterized by the relationship

where ΔPmis the peak value of the shock wave pressure at a distance between the ground and the detonation center,is the scaled distance,where R is the distance of the gauge point from the detonation center,ω1an ω2are respectively TNT equivalents of the internal and external charge,k is the reaction coefficient,and b is the attenuation index,which is related to the reactivity of the outer charge.

The relationship between the peak value of the shock-wave pressure and the scaled distance is obtained by fitting the simulation results of the peak overpressure for different initiation modes,as shown in Fig.13.

According to the relationship curve of Fig.13,the attenuation law of the peak overpressure of the composite charge with the scaled distance for different initiation modes is

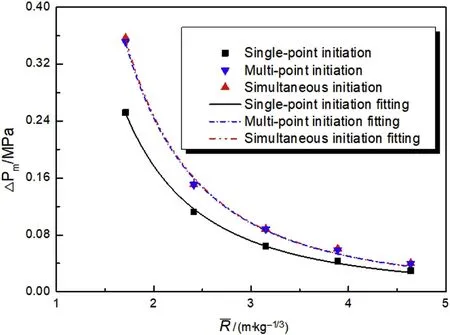
Fig.13.Relationship between the peak overpressure and scaled distance.

For three different initiation modes,the peak overpressure decreases exponentially with the scaled distance,and the attenuation exponents of different initiation modes are different.The attenuation exponent is smaller for central single-point initiation than for internal and external simultaneous initiation and external multi-point initiation.The fitting formula reveals that the reaction coefficient strongly affects the peak overpressure of the composite charge.The central single-point initiation only initiates the inner charge,and the outer charge reacts incompletely,so the reaction coefficient is small.Meanwhile,the external multi-point initiation and internal and external simultaneous initiation react with the inner and external charge,and the reaction coefficient and attenuation index are thus relatively close,as is obvious from the fitting curve of Fig.13.

4.3.Test verification

To verify the results of numerical simulation,the shock-wave pressure of composite charge for different initiation modes was measured using a shock-wave storage tester.The internal sensor was an 113B21 piezoelectric pressure sensor(United States PCB Company),and the sampling frequency was 1MSa/s.The measuring range is 50 psi and 100 psi respectively.The resonant frequency of the sensor is 300 k Hz,and the sensitivity is 50-100 m V/(lb·in-2).There were three groups of samples.Each group underwent two tests.Three initiation modes were adopted,namely central initiation,external three-point initiation,and internal and external simultaneous initiation.The detonation was initiated at the upper end.Central single-point initiation involved detonator No.8.The other initiation methods were realized using a multi-point initiation network.The multi-point initiation assembly,test samples,and assembled test charge are shown in Fig.14.

The composite charge was placed vertically on a support table with a height of 1 m.As the following formula is satisfied

Where H is the height(m)of the charge from the ground and C is the mass(kg)of the TNT charge.

The charge explosion in the test can be regarded as an in finite air explosion.Two piezoelectric pressure sensors were placed 2 m and 3 m from the vertical projection center of the composite charge,the angle between each sensor and the projection center is 60°.The receiving end face of the sensor was flush with the ground.A schematic diagram of the test site layout is shown in Fig.15.

Three different initiation modes were simulated:central singlepoint initiation,external initiation and internal and external simultaneous initiation.The central single-point initiation directly sets the initiation point in the inner charge,the external initiation sets the initiation line in the outer charge,and the internal and external simultaneous initiation sets the initiation line in the inner and external charge.For mesh size,the cell size of 0.5 cm is used before mapping,and 2 cm is used after mapping.The overpressure data recorded by the sensor at 2 m and 3 m were averaged and compared with the results of numerical simulation as shown in Fig.16.

It can be seen from Fig.16 that the test curves and simulation curves at 2 m and 3 m are consistent.

Fig.14.Charge and detonating component.

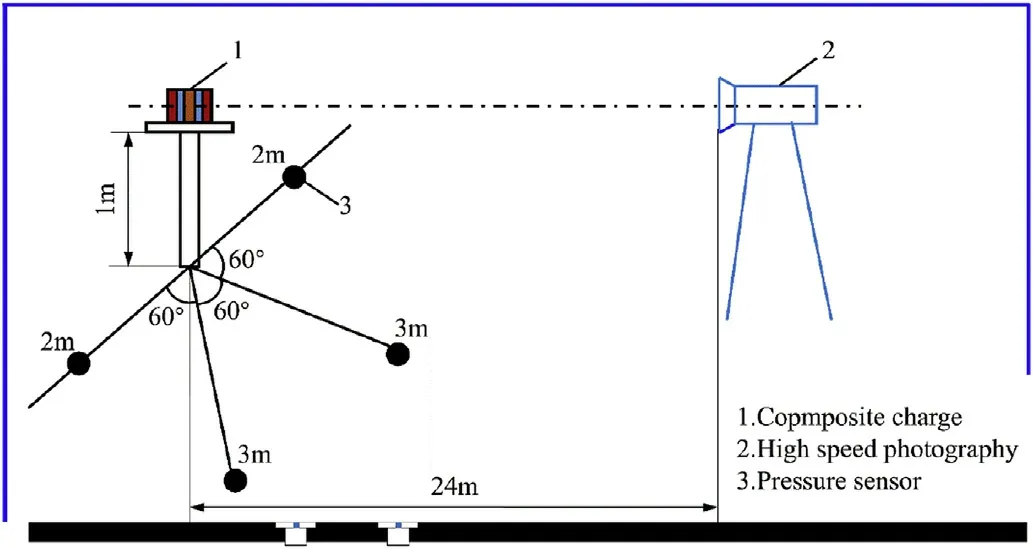
Fig.15.Schematic diagram of the test site layout.

Table 6 lists the calculated values xi,s,measured values xi,eand the error between the two characteristic parameters of the shock wave from 2 m to 3 m.The error is defined as εi=(xi,s-xi,e)/xi,e×100%),the arithmetic mean of the measured overpressures listed in Table 6.

It can be seen from Table 6 that the numerical simulation results are close to the experimental results,and the relative errors are all within 13%.Therefore,the two-dimensional axisymmetric method can be used to simulate and calculate the shock wave of the composite charge under different initiation modes.Moreover,as can also be seen in Table 6,in comparison with the central single-point initiation,the internal and external simultaneous initiation and external three-point initiation were at a distance of 2 m,the overpressure increased by 56.12%and 45.15%,respectively,and the gain at a distance of 3 m was 42.15%and 33.06%,respectively.At 2 m,the positive impulse increased by 89.19%and 60.47%,respectively.At a distance of 3 m,the gain was 29.02%and 14.93%,respectively.For the action time of the positive overpressure,the simultaneous initiation mode at different distances was lower than the central single-point and external three-point initiation.This demonstrates that the internal and external simultaneous initiation has obvious advantages with regard to improving the positive overpressure and positive impulse.

In addition,the fitting formula of the numerical simulation was verified,the test data points are merged into the fitting curve,as shown in Fig.17.

It is found by calculation that the peak value of the shock wave and the experimental value calculated by the fitting formula at different scaled distances are within 7%,indicating that the fitting formula can predict the shock wave pressure attenuation of the composite charge under different initiation modes.

5.Conclusion

(1)A finite element calculation method of the propagation of a blast wave of composite charge for different initiation modes was proposed and models of near-field and far-field explosions for composite charge were established.The effect of the cell size on the calculation of blast wave was obtained.It was found that there was convergence in the cell size range of 0.25-0.5 cm in the calculation for the near-field region and in the range of 1-3 cm in the calculation for the far-field region.The sensitivity of the positive overpressure to the cell size was higher than that of the positive impulse and the arrival time of the shockwave front,and the Euler-FCT solver was more suitable than the Euler-Godunov solver for calculating the shockwave propagation in the mapped far field.

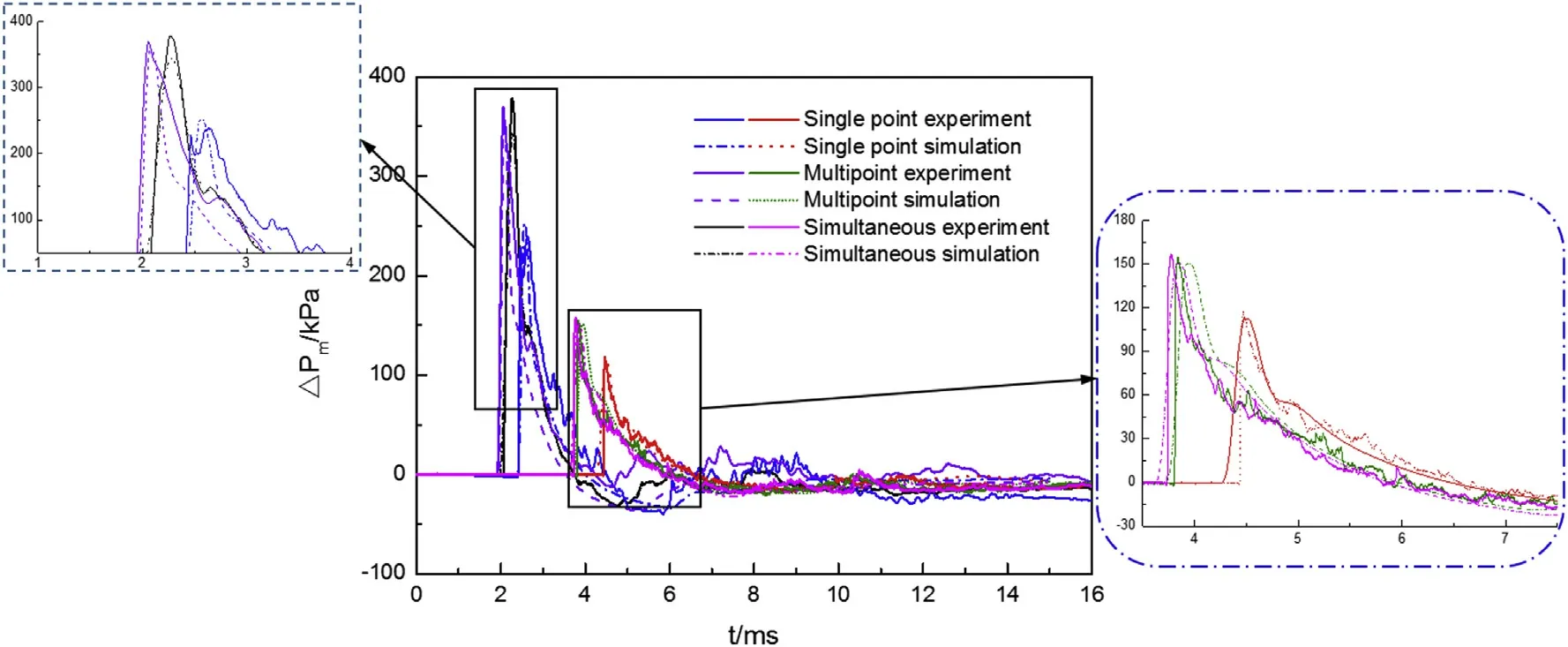
Fig.16.Comparison of measured and simulated pressure-time curves.

Table 6 Comparison of test and simulation results of the positive overpressure,positive impulse,positive duration.

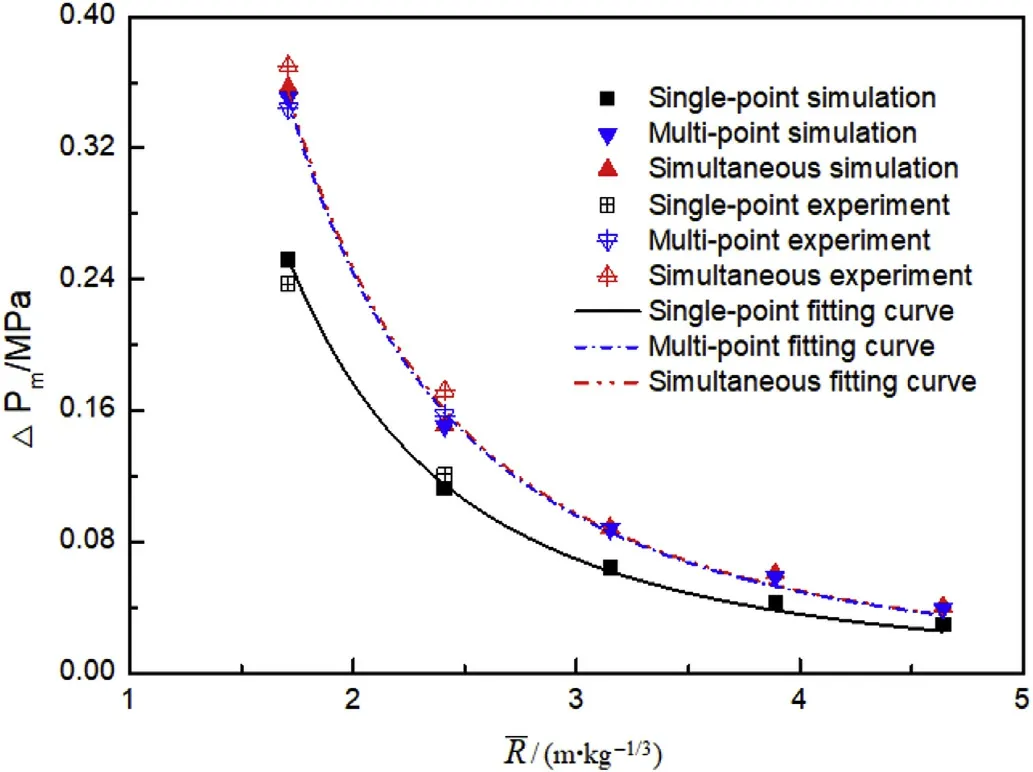
Fig.17.The relationship between peak over pressure and scaled distance.

(2)The process of propagation of the blast wave of composite charge was obtained for different detonation modes.It was found that the initiation mode has an obvious effect on the shock-wave waveform and pressure distribution of the composite charge.With increases in the propagating distance and action time of a shock wave,the magnitude of the maximum-overpressure distribution in the shock-wave area gradually increased.Meanwhile,the area of the maximumoverpressure distribution decreased in the order of internal and external simultaneous initiation＞external multi-point initiation＞central single-point initiation.

(3)The peak overpressure of the composite charge was calculated for different initiation modes;the peak overpressure of the shock wave attenuated exponentially.The equation of the attenuation of the peak overpressure of the composite charge was fitted for different initiation modes.The reaction coefficient strongly affected the peak overpressure of the composite charge for different initiation modes.

(4)The experimental results verify the dependence of the shock wave pressure of composite charge on the initiation mode.The difference between numerical calculation and experimental results(i.e.,the error)was less than 10%.It was found that the peak value of overpressure for the external threepoint initiation mode was 45.15%higher than that for the central single-point initiation mode,while that for the internal and external simultaneous initiation mode was 56.12%higher than that for the central single-point initiation mode.

Acknowledgment

The work presented in this paper has been funded by the National Natural Science Foundation of China under NO.11202103 and Qing-lan Project of Jiangsu Province.