Interface defeat studies of long-rod projectile impacting on ceramic targets

Y.X.Zhi ,H.Wu ,Q.Fng

a Amy Engineering University of PLA,Nanjing,210007,China

b Research Institute of Structural Engineering and Disaster Reduction,College of Civil Engineering,Tongji University,Shanghai,200092,China

Keywords:Interface defeat Ceramic Transition velocity Numerical simulation Parametric study

ABSTRACT The interface defeat phenomenon always occurs when a long-rod projectile impacting on the ceramic target with certain velocity,i.e.,the projectile is forced to flow radially on the surface of ceramic plates for a period of time without significant penetration.Interface defeat has a direct effect upon the ballistic performance of the armor piercing projectile,which is studied numerically and theoretically at present.Firstly,by modeling the projectiles and ceramic targets with the SPH(Smoothed Particle Hydrodynamics)particles and Lagrange finite elements,the systematic numerical simulations on interface defeat are performed with the commercial finite element program AUTODYN.Three different responses,i.e.,complete interface defeat,dwell and direct penetration,are reproduced in different types of ceramic targets(bare,buffered,radially confined and oblique).Furthermore,by adopting the validated numerical algorithms,constitutive models and the corresponding material parameters,the influences of projectile(material,diameter,nose shape),constitutive models of ceramic(JH-1 and JH-2 models),buffer and cover plate(thickness,constraints,material),as well as the prestress acted on the target(radial and hydrostatic)on the interface defeat(transition velocity and dwell time)are systematically investigated.Finally,based on the energy conservation approach and taking the strain rate effect of ceramic material into account,a modified model for predicting the upper limit of transition velocity is proposed and validated.The present work and derived conclusions can provide helpful reference for the design and optimization of both the long-rod projectile and ceramic armor.©2020 China Ordnance Society.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1.Introduction

Ceramics are widely applied as protective materials on armored vehicles on account of its high compressive strength and hardness.Meanwhile,the low density of ceramic makes it possible to reduce the total weight,which is of great significance in designing modern weight-efficient armored system.The role of ceramic plates in the interaction of high-velocity long-rod projectiles and armor is to plastically deform and decelerate the projectiles,in this scenario,there exists a special phenomenon,i.e.,the projectile is forced to flow radially on the surface of ceramic plates for a period of time without significant penetration,seen in Fig.1(a and b)[1,2].This remarkable phenomenon,know n as interface defeat,was firstly reported by Hauver et al.[3-7].

Fig.1(c)shows the dependence of the instantaneous penetration velocity of the projectile nose with the initial impact velocity of projectile v0,and three succeeding different responses of projectile with v0increasing can be found.Whenthe complete interface defeat of projectile occurs on the surface of ceramic target without substantial penetration.Wheni.e.,the dwell stage,the partial interface defeat occurs firstly and follow ed by penetrations.When,the direct penetration occurs with minimal dwell on the ceramic surface.The non-negligible kinetic energy of projectile losses due to erosion and deceleration during the dwell stage,and the ballistic performance of projectile will be obviously reduced if the dwell stage can be effectively elongated.Therefore,the interface defeat is well worth deep study for both the weapon and armored vehicle designers.The key parameters for the interface defeat are the lowerand uppervelocity bounds of dwell stage(called transition velocity),as well as the corresponding time duration(called dw ell time).

In the existing experimental work,Behner et al.[8,9]performed the reverse ballistic tests to determine the penetration dynamics and interface defeat capability of bare and buffered SiC targets against pure gold long-rod projectiles,respectively.Furthermore,the depth of penetration(DOP)tests were carried out to study the dwell characteristics of tungsten alloy long-rod projectiles impacting on the unconfined finite-thickness SiC targets[10].By using the flash X-ray radiographs,a series of reverse ballistic tests were conducted by Lundberg's group[11-13]to determine the transition velocity of different combinations of metallic(tungsten and molybdenum)long-rod projectiles and radially confined ceramic targets(SiC,B4C,TiB2,Syndie),respectively.Furthermore,the parametric influences on the transition velocity,including the hardness,fracture toughness of ceramic targets and nose shape of projectiles were discussed by Lundberg et al.[1].The oblique impacts,which are more likely occurred,were experimentally studied by Anderson et al.[14],in which the interface defeat and dwell time of pure gold projectile impacting SiC targets with the obliquity of 30°,45°and 60°are compared with the normal impacting scenarios.The details of the above tests will be given in Section 2.

As for the numerical simulation work,by adopting the 2D meshless projectiles and 2D Lagrange finite elements for ceramic targets which are then automatically convert into meshless particles due to severe distortions,Holmquist and Johnson[15-18]numerically examined the dynamic responses of ceramic targets subjected to the high-speed projectile impacts,including the complete interface defeat,dwell and direct penetration scenarios.By establishing the projectile and SiC target with SPH(Smoothed Particle Hydrodynamics)particles and Lagrange finite elements,Quan et al.[19]compared the numerical predictions of interface defeat for confined targets with the experimental observations draw n by Lundberg et al.[11],in which JH-1 model[20]was adopted to describe the ceramic material.Chi et al.[21]further proposed a numerical technique to apply the prestress on the confined ceramic targets with the non-linear analysis program AUTODYN[22],and the effects of different prestress condition,i.e.,radial,axial,and hydrostatic,on the impact resistance of ceramic targets and interface defeat were discussed.

The existing theoretical analyses on the interface defeat are mainly concentrated in the predictions of the lower and upper bounds of transition velocity as well as the dwell time.By assuming the approximate radial distribution of the normal pressure loading on the ceramic target during projectile penetrations,the expression of the transition velocity was given by Lundberg et al.[11],which was validated by the tests of different projectiles/ceramic targets combinations.Based on the Alekseevskii-Tate(A-T)model[23,24],Anderson and Walker[2]presented an analytical model that captures the essential mechanics of interface defeat and dw ell,which was validated by both the small arms and long-rod projectile impacting test on ceramic targets.Li et al.[25,26]extended the Alekseevskii-Tate(A-T)model[23,24]to predict the penetration velocity decay as well as the mass loss of flat and conical nosed long-rod projectiles during the interface defeat.By taking the Hugoniot elastic limit(HEL)of ceramic material into account,Li et al.[26]modified the lower bound of transition velocity initially proposed by Lundberg et al.[11].Furthermore,the transition velocity and dwell time for the oblique impact were discussed by Li and Chen[27],and the corresponding comparisons with the normal impact scenario were performed.

Generally,the systematic experimental studies on the interface defeat of long-rod projectiles normally and obliquely impacting bare,buffered and confined ceramic targets have been conducted.Nevertheless,the corresponding numerical simulation work as well as the related parametric influences are rarely reported.Besides,the upper bound of transition velocity vupper0proposed by Lundberg et al.[11]and Liet al.[26]are deviated from the corresponding test results.At present,by adopting the SPH particles and Lagrange finite elements for projectiles and ceramic targets,the existing tests of interface defeat[8-14]are firstly numerically simulated,and the transition velocity and dwell time are discussed comprehensively.Then,based on the validated numerical algorithm,constitutive model and parameters,the parametric analyses,including the projectile,constitutive models of ceramic,buffer and cover plate as well as the prestress acted on the target are numerically performed.Finally,based on energy conservation approach and taking the strain rate effect of ceramic material into account,a modified model for predicting the upper bound of transition velocity is proposed.

2.Numerical simulations of the existing tests

Systematic experimental studies on the interface defeat of ceramic targets were carried out successively by Behner,Lundberg,and Anderson's group from 2000 to 2011[8-14].Table 1 summarizes the main parameters of projectiles and targets,where ρpand ρtare the densities of projectile and target,L and D are the length and diameter of projectile,respectively.The corresponding target configurations,i.e.,bare or buffered target(Type I),radially confined target with cover and back plates(Type II),and bare or buffered oblique target(Type III)are given in the last column of Table 1.

2.1.Behner's test[8-10]

2.1.1.Pure gold projectiles impacting bare and buffered SiC ceramic targets

Firstly,the pure gold projectile penetration test on bare SiC ceramic target[9]is numerically simulated to calibrate the related parameters of pure gold.During the test,two typical pure gold long-rod projectiles with the diameters of 0.75 mm and 1.00 mm and lengths of 50 and 70 mm were used,and the ceramic targets were SiC-N regular cylinders with a diameter of 20 mm and a length of 35 mm,respectively.As shown in Fig.2 and D axisymmetric models of the pure gold long-rod projectile and the bare SiC ceramic target were established in AUTODYN[22].Considering the response of radial flow during the dwell stage and large deformation in the subsequent penetration stage,the projectile was discretized into SPH particles.The projectile particles were permitted to move freely without the restriction of the grid.The SPH particle size is chosen as 0.125 mm,which guarantees the values of SPH particles along the radius and diameter of projectile are both integer.It is also identical with which adopted by Quan et al.[19]and Chi et al.[21].Besides,the SiC ceramic target was represented in Lagrange algorithm,taking the efficiency and accuracy of computation into account,the mesh size is determined as 0.25 mm by trial and error.

Considering that the comprehensive parameters of pure gold were rarely reported,the Von Mises constitutive model with linear Equation of State(EOS)and plastic strain failure model was selected to describe the behavior of pure gold.Based on the shear modulus G and the Poisson's ratio νgiven by Steinberg[28],the bulk modulus K of pure gold can be derived,i.e.,K= 2（1+ ν）G/3（1-2ν）=165.67 GPa.As for SiC ceramic,the JH-1 model embedded in the AUTODYN material library[22]was selected with adding an erosion algorithm to ensure the continuity of computing.The maximum strength of the failed ceramic Sfmaxin JH-1 model can not be determined directly.At present,similar with the existing work[16],by trial and error,Sfmaxof SiC and the plastic strain of the pure gold are determined as 0.45 GPa and 0.15 based on the direct penetration test[9].The adopted parameters of pure gold and SiC ceramic are listed in Table 2.The comparisons between the numerical and experimental penetration depth and residual length of projectile[9]are illustrated in Fig.3(a).Furthermore,the comparisons between the numerical images and the flash X-ray photographs[9]at different time instants are further shown in Fig.3(b).The excellent agreements between the simulation results and the experimental data can be found,thus the correctness and applicability of the constitutive model parameters and numerical algorithm of the pure gold and SiC ceramic are both verified.

Fig.2.2D axisymmetric numerical models of projectile and target.

Table 1 Details of the interface defeat test.

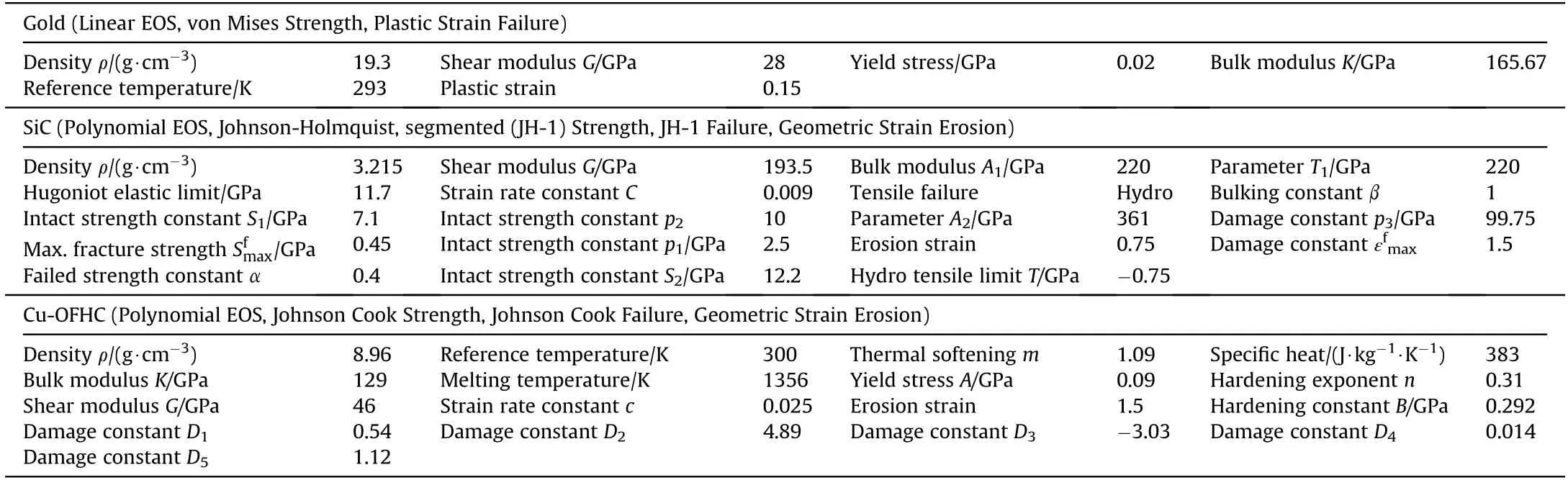
Table 2 Parameters of pure gold,SiCand Cu.

For the interface defeat test,the transition velocity for pure gold long-rod projectile with diameter of 1 mm and a length-todiameter ratio of 70 impacting bare SiC ceramic target was obtained experimentally as 776-958 m/s[8].Based on the numerical algorithm and model parameters validated above,the numerical simulation of the shots with striking velocities of 776 m/s and 958 m/s were performed,respectively.The corresponding numerically simulated impact processes are shown in Fig.4.It can be seen from Fig.4(a)that the complete interface defeat of projectile occurs on the surface of SiC ceramic target,while no obvious penetration is happened.Comparably,in Fig.4(b),a minor penetration can be seen at 6μs,which is close to the experimental dwell time value of 6.25μs[8].

For the buffered target,the simulation of SiC ceramic with a front 2 mm-thick copper buffer subjected to the impact of pure gold long-rod projectile was further performed.CU-OFHC in the standard material library in AUTODYN[22]was adopted to model the behavior of the copper,and the parameters of which are listed in Table 2.The mesh size of the copper buffer was identical with that of the ceramic target(0.25 mm)and the calculation algorithm and model parameters are identical with that in Section 2.1.1.The simulated impact process with the striking velocities of 1578 m/s is shown in Fig.5(a).Fig.5(b)further shows the comparisons between the numerical and experimental penetration depth as well as the residual length of projectile[9],where the interface between the buffer and ceramic is identified as the initial penetration depth of 0 mm.It can be seen from Fig.5(b)that,after perforating the copper buffer,the dw ell of the projectile occurs at the time instant of about 2.6μs and lasts to about 9.1μs.Therefore,the dw ell time is about 9.1-2.6=6.5μs,which is close to the experimental data of 7μs[9].During the dwell stage,the residual length of projectile reduces by 7.6%with no penetration occurs,which further addresses the significance of dwell in the design of ceramic armor under long-rod projectile impact.

2.1.2.Tungsten projectiles impacting SiC/RHA steel composite targets

For the tungsten projectiles impacting SiC/RHA steel composite targets conducted by Behner et al.[10],the corresponding 2D axisymmetric model was established,as shown in Fig.6.Similarly,the projectile was discretized into SPH particles with the size of 0.125 mm,and both the SiC ceramic and RHA steel were modeled in Lagrange algorithm with the mesh size of 0.25 mm.

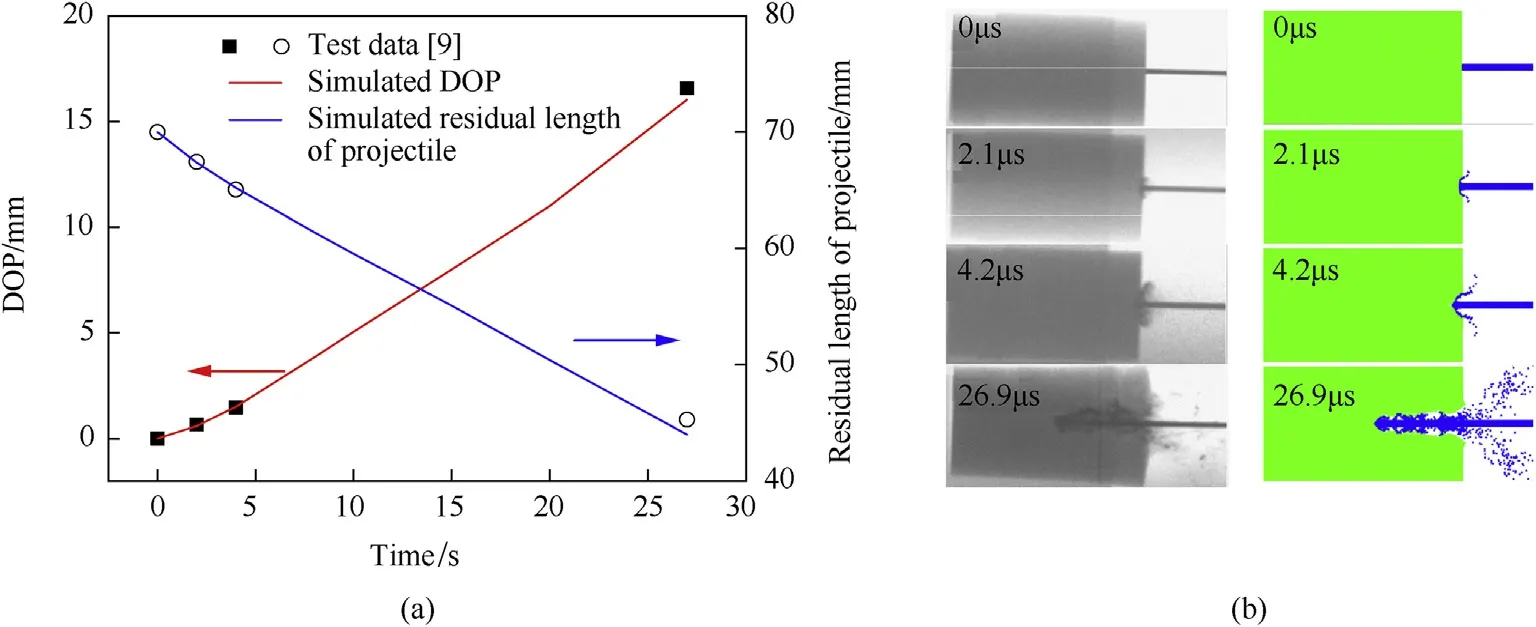
Fig.3.Experimental and numerical simulation results(a)DOP and residual length of projectile(b)penetration process.

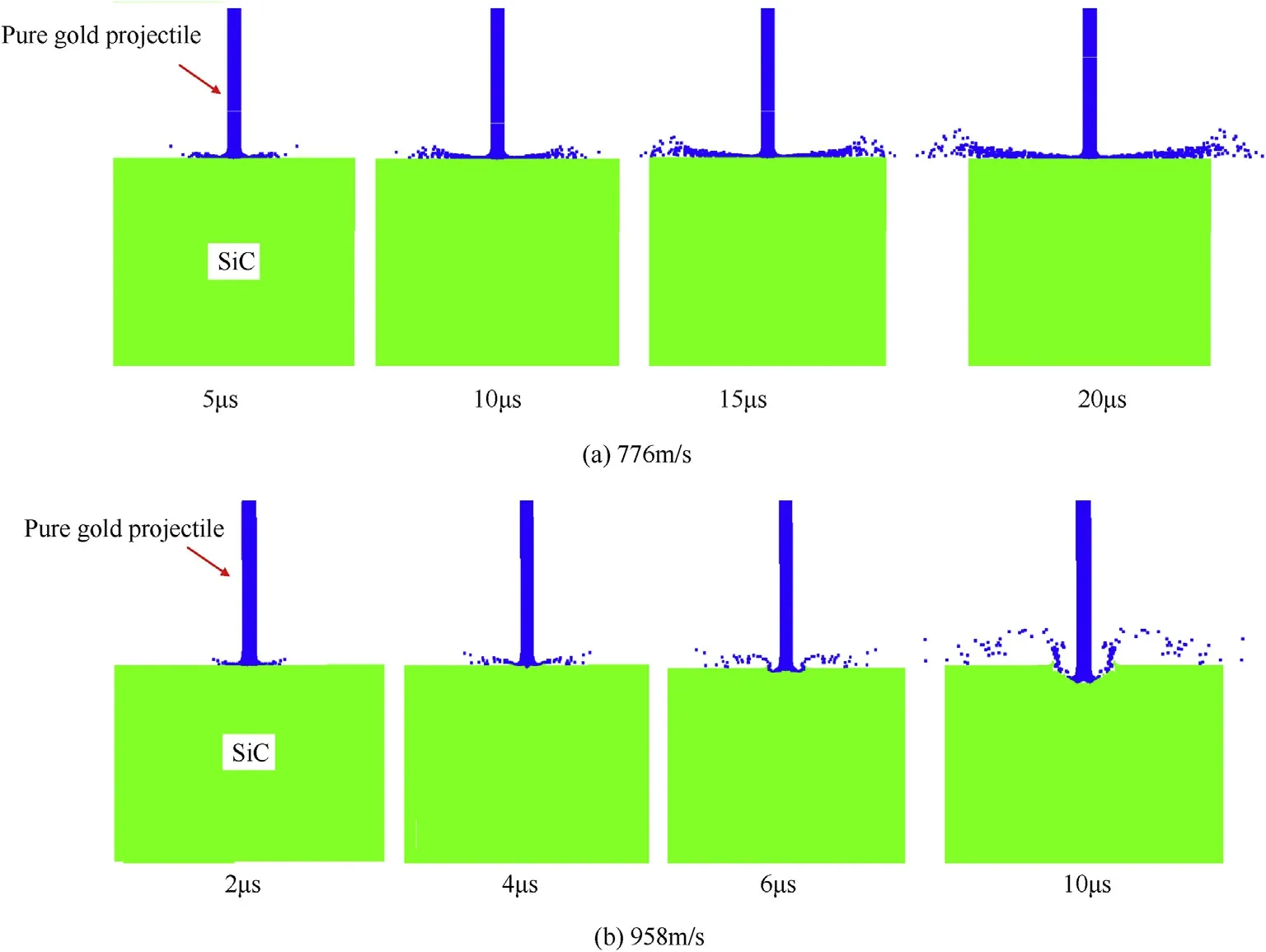
Fig.4.Simulated impact process of pure gold long-rod projectile impacting bare SiC ceramic target with the striking velocity of(a)776 m/s(b)958 m/s.

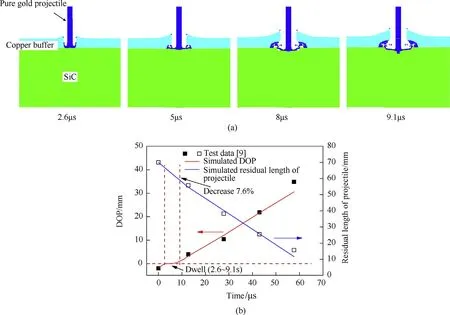
Fig.5.Pure gold long-rod projectile impacting buffered SiC ceramic target with striking velocity of 1578 m/s(a)simulated impact process(b)comparisons.

The corresponding parameters are listed in Table 3.The comparisons between the simulated and experimental total areal density of the penetrated materials,as well as the impact process with striking velocities of 525 m/s and 1356 m/s are given in Fig.7.Obviously,good agreements are obtained.Two different responses,i.e.,the radial flow and splash of projectile as well as the direct penetration with few projectile particles ejecting outwards,are reproduced,which are consistent with the experimental observations draw n by Behner et al.[10].

Fig.6.2D axisymmetric models of projectile and target.

2.2.L undberg's test[11-13]

The 2D axisymmetric models of projectile and target were established and shown in Fig.8,in which the numerical algorithm as well as the mesh size were identical with those adopted in Section 2.1.The model parameters of 4340 steel and Mar 350 steel are listed in Table 3.

The numerical simulations of tungsten alloy long-rod projectiles impacting confined SiC ceramic targets with striking velocities of 1410 m/s,1645 m/sand 2175 m/s were carried out,respectively.The corresponding impact process at different time instants,as well asthe comparisons between the simulated and experimental penetration depths(the interface between 4340 steel cover plate and SiC ceramic is identified as the initial penetration depth of 0 mm)are shown in Fig.9.It can be seen that,the numerical simulations can reproduce the three different responses of the projectiles with increasing the initial velocity,i.e.,complete interface defeat,dwell(for about 6μs)and direct penetration.Simultaneously,good agreements between the simulated and experimental DOP can be found.

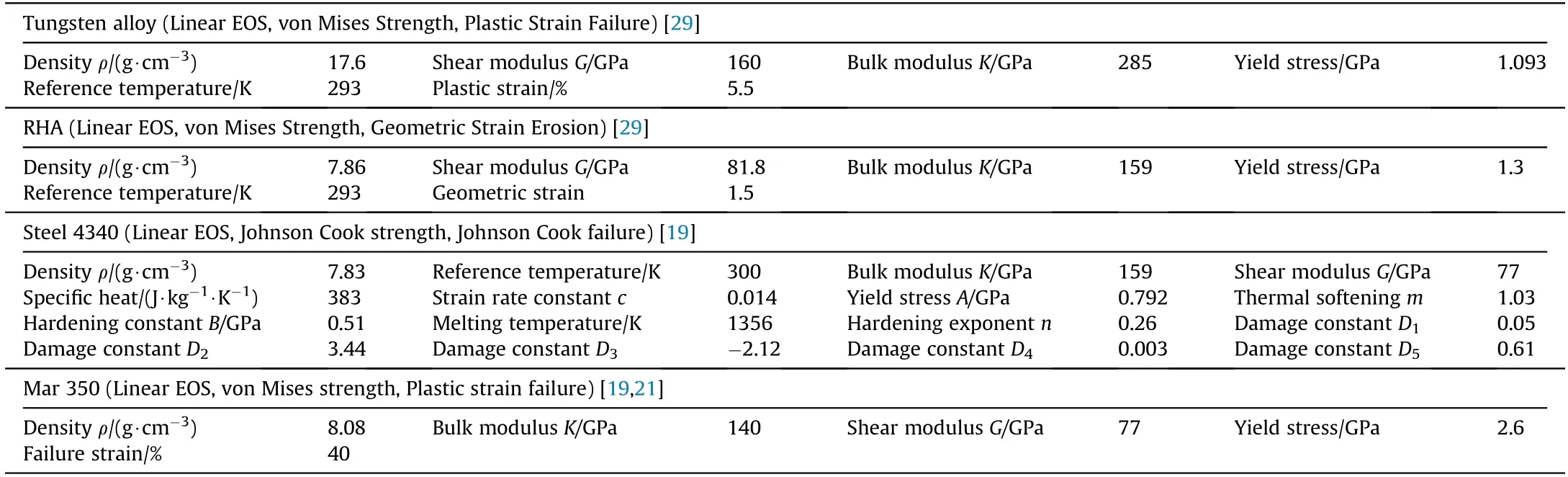
Table 3 Parameters of tungsten alloy,RHA,4340 steel and Mar 350.

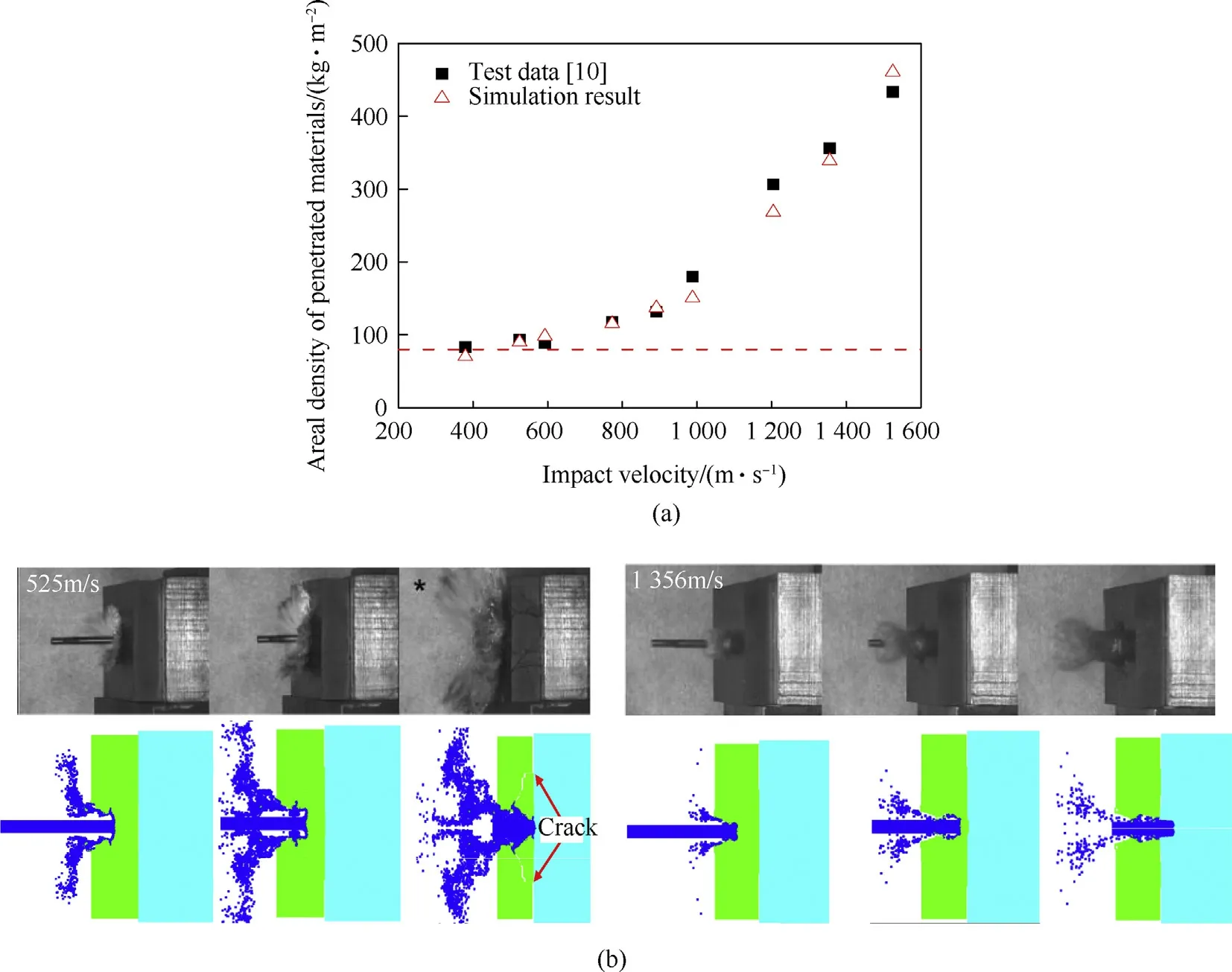
Fig.7.Comparisons between the simulated and experimental(a)total areal density of penetrated materials(b)impact process.

Fig.8.2D axisymmetric model of projectile and target.

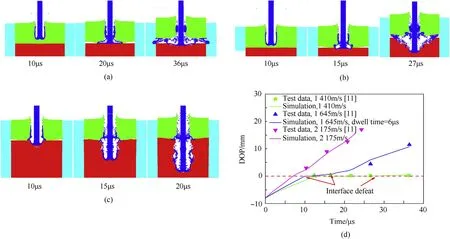
Fig.9.Comparisons between the simulated and experimental results(a)1410 m/s,complete interface defeat(b)1645 m/s,dwell(c)2175 m/s,direct penetration(d)penetration depth.

2.3.Anderson's test[14]

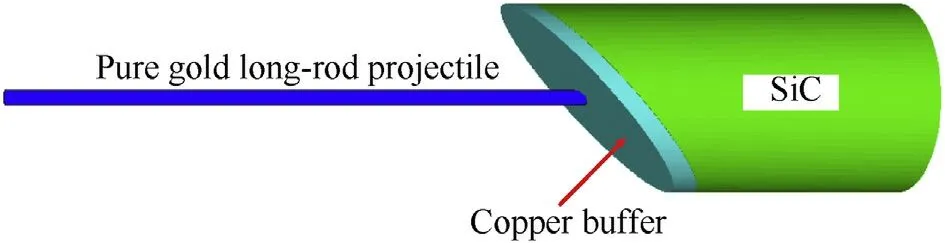
Fig.10.3D models of the projectile and the oblique buffered ceramic target.

Considering the asymmetric test setup of the oblique impact,Fig.10 illustrates the 3D models of projectile and the oblique buffered ceramic target,in which the pure gold long-rod projectile was similarly discretized into SPH particles with the particle size of 0.125 mm.The 3D models of both the oblique SiC ceramic and copper buffer were also established in using Lagrange algorithm with the mesh size of 0.25 mm.

Based on the material parameters of pure gold and SiC ceramic given in Table 2,for ceramic targets with obliquities of 45°and 60°,Fig.11 shows the comparisons between the simulated and the experimental penetration depths and residual lengths of projectile,respectively.Comparisons between the simulated impact images(including the cross-sections of the penetrated ceramic targets in Fig.12(d))and the experimental flash X-ray photographs[14]at different time instants are further given in Fig.12.It can be seen that the simulation results are in good agreement with the experimental data,the responses of complete interface defeat and dwell are both reproduced numerically.

Furthermore,the numerical simulation of a copper-buffered oblique SiC ceramic target impacted by pure gold long-rod projectile was undertaken,and the parameters of copper material were listed in Table 2.Fig.13 shows the comparisons between the simulated and experimental penetration depths and the residual lengths of projectile for ceramic targets with obliquities of 30°,45°and 60°,and the corresponding comparisons of the impact process are further given in Fig.14.Obviously,good agreements between the simulation results and the experimental data as well as the flash X-ray photographs are derived.

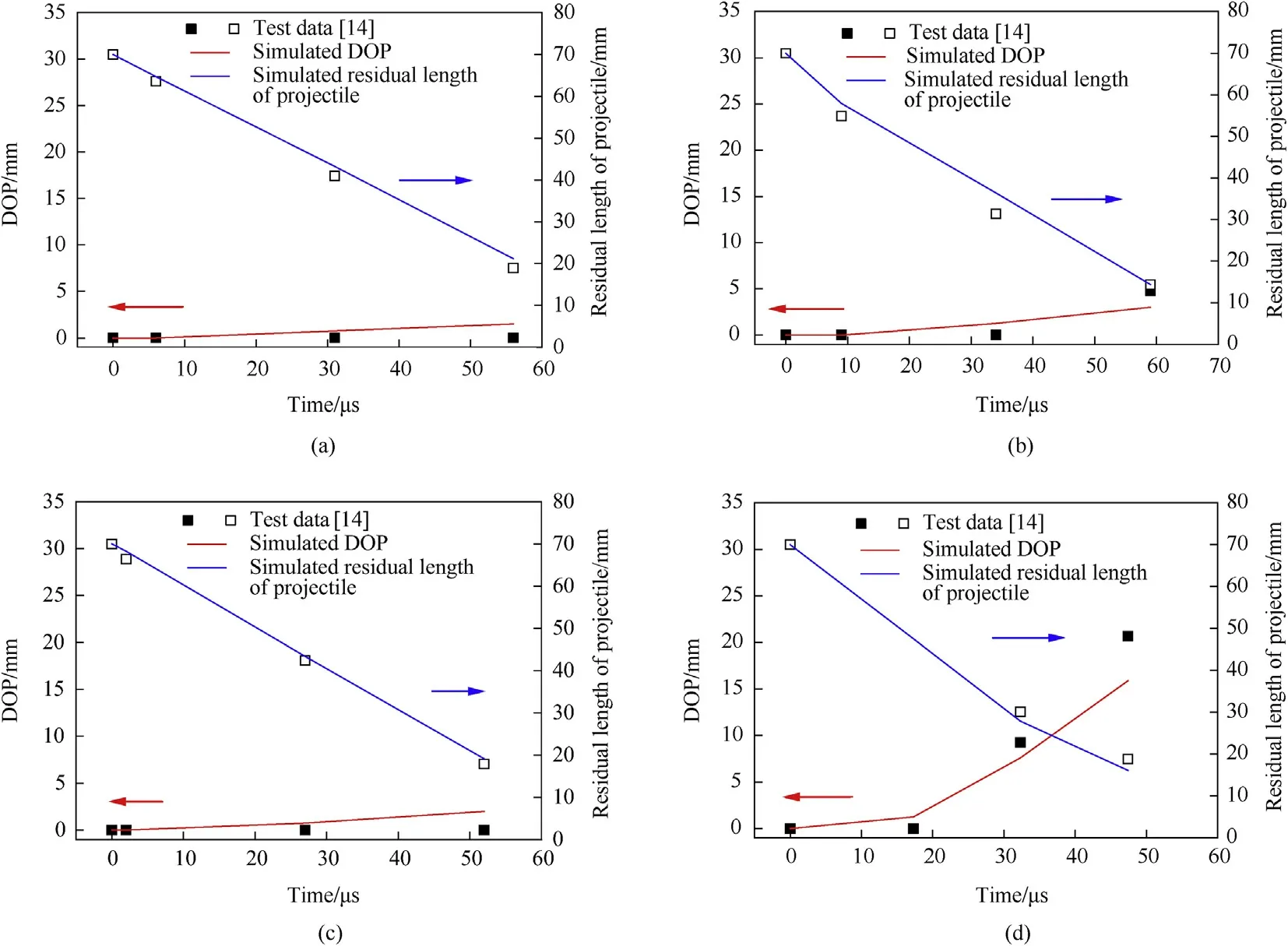
Fig.11.Comparisons between the simulated and experimental penetration depths and residual lengths of projectile(a)45°targets,930 m/s,complete interface defeat(b)45°targets,1015 m/s,dw ell(c)60°targets,1008 m/s,complete interface defeat(d)60°targets,1515 m/s,dw ell.

In this section,the numerical simulations of the existing tests of interface defeat were systematically carried out.Good agreements betw een the numerical predictions and experimental measurements are obtained in various impact scenarios.Meanwhile,different responses of the projectile,i.e.,complete interface defeat,dwell and direct penetration are all reproduced well numerically.Therefore,the numerical algorithm,constitutive models and the corresponding material parameters are validated,which are further adopted in the following parametric studies.

3.Parametric influences on interface defeat

In this section,based on the above validated numerical algorithm as well as the corresponding constitutive models and parameters of both the projectiles and targets,the influences of projectile(material,diameter,nose shape),constitutive models of ceramic(JH-1 and JH-2 models[20,30]),buffer and cover plate(thickness,constraints,material),as well as the prestress acted on the target(radial and hydrostatic)on the interface defeat(transition velocity and dwell time)are systematically investigated.

3.1.Projectile

The pure gold long-rod projectile impacting on bare SiC ceramic target[8]is taken as the control test,the influences of the material,diameter and nose shape of projectile on the interface defeat are discussed.

3.1.1.Material

Three different projectile materials,i.e.,tungsten,gold and molybdenum,were chosen to study the influences of projectile material on the interface defeat characteristics.The models of projectiles with three different materials,as well as identical mass and diameter were established,the corresponding density ρ and dynamic yield strength σypare listed in Table 4,and the numerical algorithm and mesh size are identical with those adopted in Section 2.1.The numerically predicted transition velocity for three different projectiles impacting bare SiCceramic target are given in the first three row s of Table 4.The transition velocity of 920-1180 m/s for pure gold projectile impacting bare SiC ceramic target is determined numerically,which is consistent with the experimental observations that the complete interface defeat and dwell lasted for about 7μs occurred at the striking velocity of 776 m/s and 958 m/s,respectively[8].Furthermore,it can be seen from Table 4 that,under the identical impacting scenario,the transition velocity of pure gold projectile is the highest on account of its lowest yield strength,and then is the tungsten alloy projectile,which is followed by the molybdenum projectile.

3.1.2.Diameter

The influence of the projectile diameter on the interface defeat is discussed by changing the projectile shank diameter while keeping the projectile total mass unchanged.The numerical algorithm as well as the mesh size remain unchanged,and the corresponding geometry size of the projectiles and the simulation results are given in the middle four row s of Table 4.Under the impact of pure gold projectiles with different diameters and initial striking velocities of 920 m/s,Fig.15 shows the distributions of Von Mises stress in SiC ceramic targets at the same time instant of 3μs,respectively.It can be seen that,the wider distributions of Von Mises stress and larger damage areas occur for the relatively larger projectile diameters,i.e.,1.5 mm and 2 mm.Besides,the upper bound of the transition velocityincreases gradually,i.e.,the direct penetration capacity of gold projectile into the bare ceramic target is weakened with increasing the diameter of projectile.Meanwhile,the lower bound of the transition velocitydecreases gradually,which indicates that complete interface defeat will occur easier with increasing the diameter.

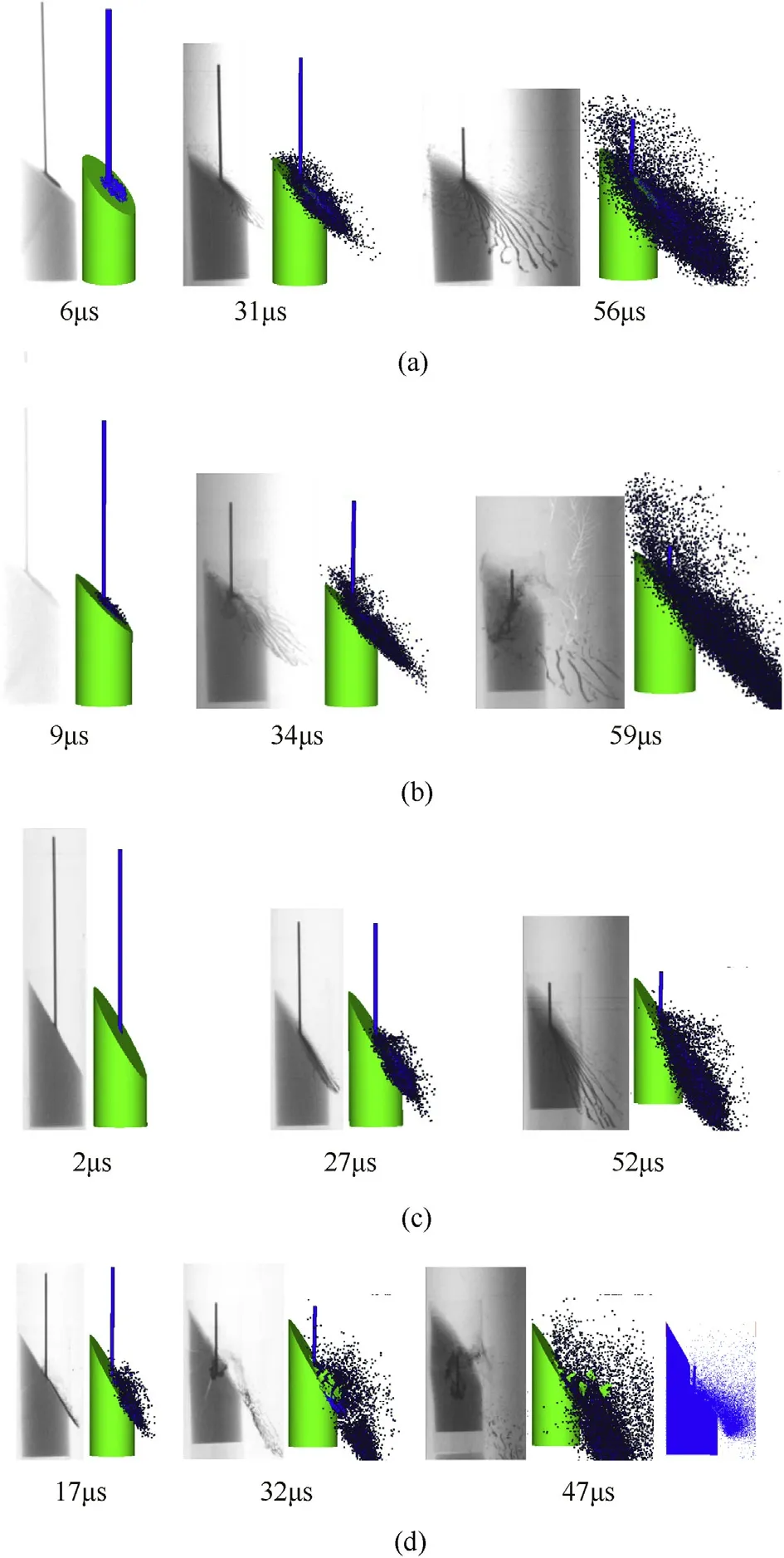
Fig.12.Comparisons between the flash X-ray images[14]and simulated results(a)45°target,930 m/s(b)45°target,1015 m/s(c)60°target,1008 m/s(d)60°target,1515 m/s.

3.1.3.Nose shape

The influence of projectile nose shape on interface defeat is discussed by changing the nose shape while keeping the projectile total mass unchanged.The numerical algorithm as well as the mesh size remain unchanged.The schematic diagram and geometric sizes of the projectiles with different nose shapes are given in Fig.16(a)and Table 4,respectively.Fig.16(b)further shows the damage distributions in SiC ceramic targets at the same instant of 5 μs for the three impacting scenarios,in which the initial striking velocities are 1100 m/s.Different responses,i.e.,penetration,dwell(from interface defeat to penetration)and interface defeat,corresponding to the three different nose shapes can be seen in Fig.16(b).The comparisons of the numerically derived transition velocities for the three projectile nose shapes are listed in the last three rows of Table 4.It indicates that,compared with the flat nosed projectile,the influence of hemispherical nose is slightly(the upper and lower bounds of the transition velocity decrease by 6.68%and 5.43%),while the truncated conical nose can significantly increase the lower limit of the transition velocity(the upper and lower bounds of the transition velocity increase by 4.24%and 19.57%).Based on Fig.16,it indicates that,the initial contact area between the truncated conical nose projectile and the ceramic target is the smallest,which prolongs the damage accumulation period of ceramic target.Moreover,the ballistic performance of the truncated conical projectile will be reduced on account of the continuous defeat of the nose and the decreasing velocity.Therefore,the truncated conical projectile leads to the highest transition velocity.

3.2.Constitutive models of ceramic

3.2.1.Introduction of JH-1 and JH-2 models[20,30]

JH-1 and JH-2 constitutive models[20,30]are applicable to describe the dynamic responses of brittle materials such as ceramics subjected to large strains,high strain rates and high pressures.As shown in Fig.17,JH-1 strength model adopts a linear yield surface in which the complete strength includes two inflection points(p1,S1)and(p2,S2),and the residual strength contains the damage parameter α and the maximum residual strength parameter Sfmaxof the fractured ceramic.As for JH-2 strength model,nonlinear normalized yield surface is adopted in which the expressions of the intact strength σ*iand the fracture strength σ*fare

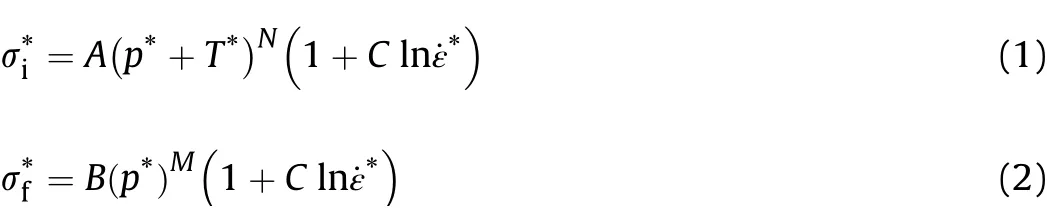
where A and N are the intact strength coefficient and exponent,B and M are the fracture strength coefficient and exponent,respectively.The normalized pressure is p*=p/pHEL,where p is the actual pressure and pHELis the pressure at the HEL.The normalized maximum tensile hydrostatic pressure is T*=T/pHEL,where T is the maximum tensile hydrostatic pressure the ceramic can withstand.

As shown in Fig.17,JH-1 and JH-2 models are essentially different in describing the relationship between the strength and the accumulated damage of ceramic materials.JH-1 model deems that the strength of ceramic will not decrease during the damage accumulation process,but it will drop to the residual strength instantaneously when the ceramic is completely damaged(D=1.0).Comparably,in JH-2 model,the strength of ceramic decreases gradually in the process of damage accumulation and will drop to the residual strength terminally when the ceramic is completely damaged(D=1.0).Grady and Moody[31]found that the strength of ceramic materials decreased slightly even under high impact pressure(about 20-30 GPa)while considerable damage has accumulated.It indicated that ceramics would maintain relatively complete strength for a certain period of time during the damage accumulation process.Furthermore,Holmquist and Johnson[16]pointed out that the JH-1 model was more accurate in describing the relationship between strength and damage accumulation of ceramic materials and was more suitable for numerically describing the interface defeat phenomenon than JH-2 model.

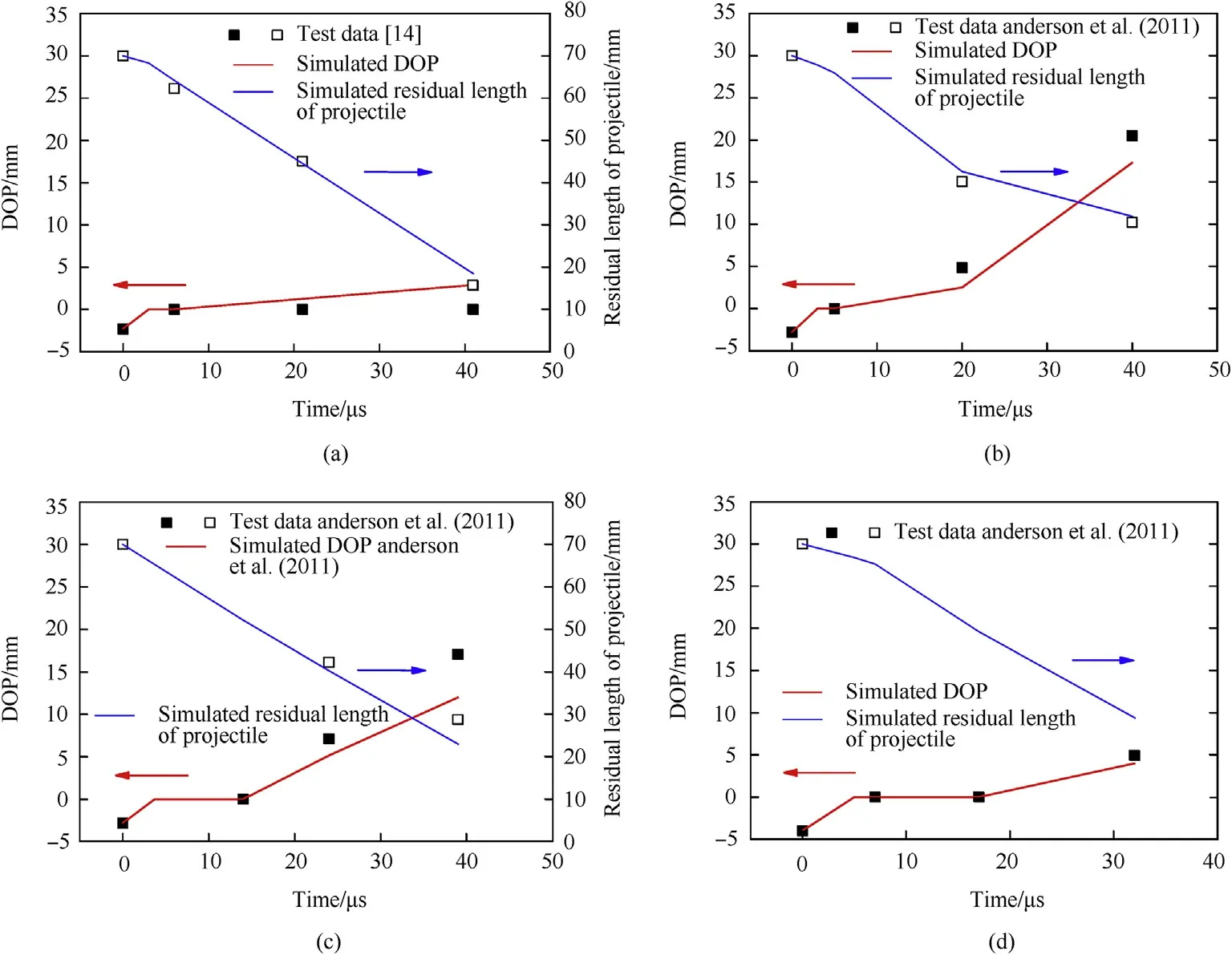
Fig.13.Comparisons between the simulated and experimental results(a)30°targets,1419 m/s,complete interface defeat(b)30°targets,1529 m/s,dwell(c)45°targets,1545 m/s,dwell(d)60°targets,1548 m/s,dwell.

3.2.2.Numerical simulation of interface defeat with JH-1 and JH-2 models

The validations of JH-1 and JH-2 models have been verified comprehensively in different impact scenarios[15-21]whereas the systematical comparisons of these two models for interface defeat are limited.In this section,the normalized intact yield surface of JH-2 model is obtained by fitting the parameters of JH-1 model,and the corresponding comparisons of interface defeat simulated by above two models are further performed.

As shown in Fig.18,based on the parameter pairs((p1,S1),(p2,S2))and the hydrostatic tensile limit T of JH-1 strength model(listed in Table 2),as well as the data proposed by Grady and Moody[31]for SiC ceramic,the parameters of A=0.69 and N=0.4 of the normalized intact yield face in JH-2 strength model are derived by fitting the intact strength surface of JH-1 model.Furthermore,based on the maximum fracture strength parameter Sfmaxvalidated in Section 2.1.1,the normalized residual strength parameters of B=0.0414 and M=0.107 in JH-2 model are determined.In summary,the parameters of JH-2 model are given in Table 5,and it is worth noting that the parameters except for the intact and fractured strength models are referred from Holmquist and Johnson[16]and Cronin et al.[32].

As for pure gold long-rod projectile impacting on bare SiC ceramic target(simulated by JH-1 model),the maximum velocity of complete interface defeat of projectile was obtained numerically as 920 m/s(seen in Section 3.1.1 for details).Keeping the numerical algorithm as well as the mesh size unchanged,the corresponding numerical simulation by JH-2 model with the identical striking velocity was further conducted.It is found that about 8μs of the dwell time is obtained before the penetration into SiC target occurs.The distributions of Mises stress and damage in ceramic target at the time instant of 8μs described by JH-1 and JH-2 models are further given in Fig.19(a),respectively.It can be seen that,there is not much differences between the maximum Von Mises stress in the ceramic target predicted by above two models,while the distribution of damage area in JH-1 model is much wider than that in JH-2 model.At 8μs after the projectile impacting on the target,the occurrence of interface defeat phenomenon is predicted by JH-1 model,while the penetration has already begun simulated by JH-2 model.Besides,as for the partial interface defeat scenario,about 7μs of dwell was derived experimentally[8]when the striking velocity of pure gold increased up to 958 m/s.Similarly,the distributions of Mises stress and damage at the time instant of 7μs derived numerically by JH-1 and JH-2 models are given in Fig.19(b).Accumulation of damage can be seen in JH-1 model with the ceramic remains almost intact,which indicates that the dwell response occur.While in the JH-2 model,the fractured region(D=1)can be seen,which indicates that the penetration has already begun.

In conclusion,compared with JH-2 model,JH-1 model is more suitable to describe the relationship between the strength and damage accumulation of ceramic material under projectile impact,and thus more accurate to reproduce both the complete and partial interface defeat characteristics.

3.3.Buffer and cover plate

The brittleness and significant decrease of penetration resistance of damaged ceramic make it unsuitable as a single target to resist the projectile impact.Therefore,buffers and cover plate are always attached to the front face of ceramic target to weaken the impact pressure as well as to enhance the interface defeat.It should be pointed out that the influence of buffer thickness may be varied on account of the material and geometric dimensions of projectiles and targets.Behner et al.[9]pointed out that the buffer thickness had a non-negligible effect on the dwell time of interface defeat.Crouch et al.[33]found that attaching a copper buffer would attenuate the shock stress and lead to a relatively gradual loading to the ceramic,which resulted in limiting the dwell of small-caliber projectile with deformable mild steel cores and striking velocities of～700 m/s.The main purpose of this section is to discuss the influence of buffer thickness on the dwell of long rods.Besides,as for the relatively thick cover plate,the focus is paid on the configuration and material of the cover plate at present.

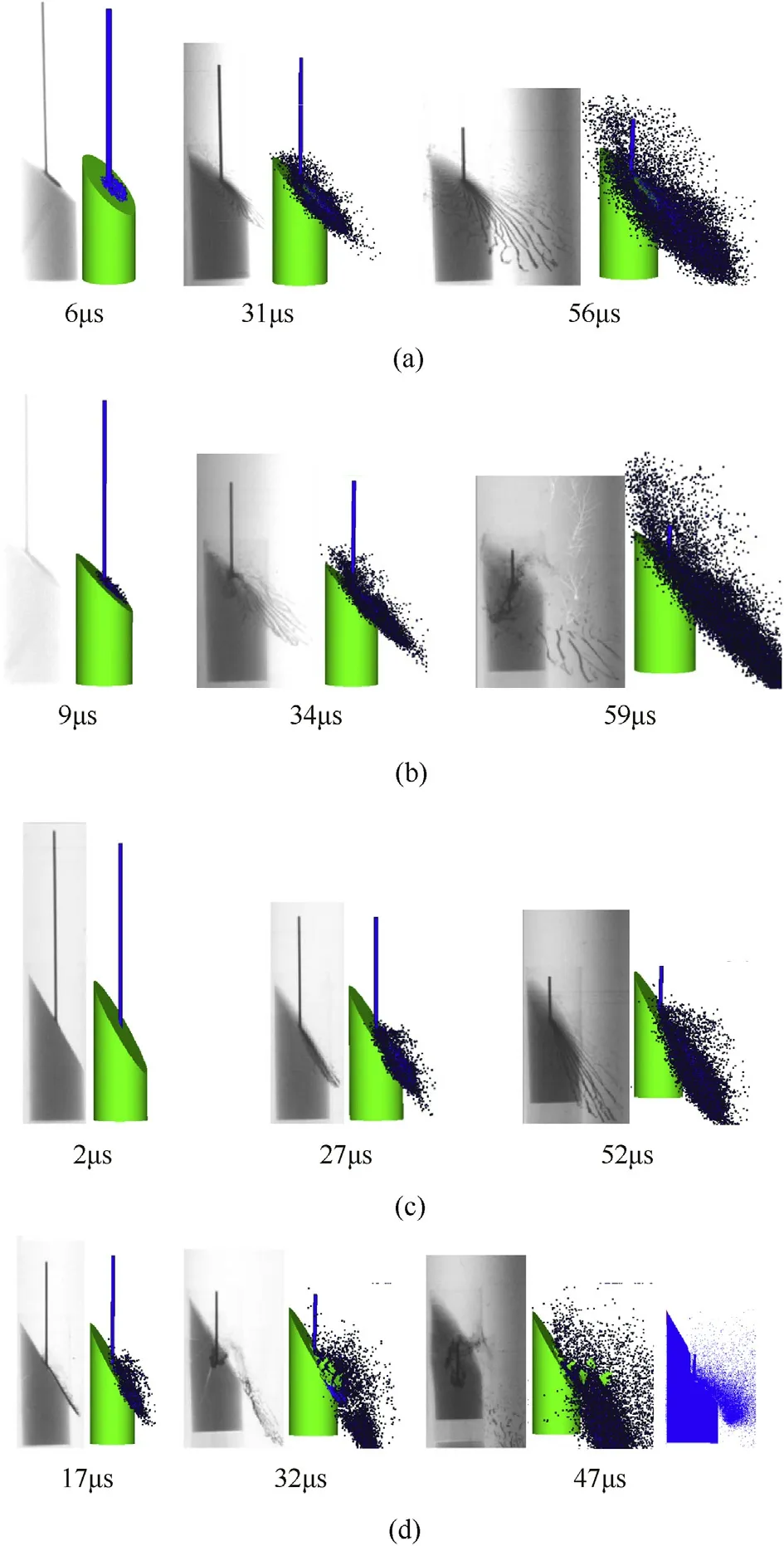
Fig.14.Comparisons between the flash X-ray images[14]and simulated results(a)30°target,1419 m/s(b)30°target,1529 m/s(c)45°target,1545 m/s(d)60°target,1548 m/s.

3.3.1.Thickness of buffer

Taking pure gold long-rod projectile impacting 2 mm-thick copper-buffered SiC target as the control test(see in Section 2.1.1),the related impact scenarios of bare,3 mm-thick and 4 mm-thick copper-buffered targets are further numerically simulated to discuss the influence of buffer thickness on the interface defeat characteristics.Fig.20 shows the corresponding numerical simulation results of DOP.Compared with the bare target,obvious dwell stage can be induced by attaching buffers to the front face of the ceramic target.It is noteworthy that the 3 mm-thick buffer can prolong the dwell time to about 8μs while the corresponding dwell time elongation of 4 mm-thick buffer is about 6μs,which indicates that the dwell time cannot be prolonged monotonously with increasing the buffer thickness.One possible reason lies in that the radial flow of projectile material will be constrained when the buffer thickness exceeds a critical value,thus there exists an optimal thickness of buffer.The simulation results are consistent with the experimental observations from Behner et al.[10],in which the 3 mm-thick copper-buffered target leads to the highest transition velocity,follow ed by 2 mm-thick and 4 mm-thick buffer.

3.3.2.Constraints of cover plate

Taking the test of tungsten alloy projectile impacting the confined SiC target(free constraints of 4340 steel cover plate)with the striking velocity of 1645 m/s[10]as reference,the influence of cover plate configuration is studied by further applying the fixed restraints to the cover plate.Fig.21 shows the comparisons of the simulated DOP and the corresponding impact images at different time instants,respectively.It can be seen that,compared with the scenario of free cover plate,the fixed cover plate can further prolong the dwell time for about 4μs and can effectively reduce the damage area of ceramic target.Furthermore,the final DOP is reduced by about 10%when applying the fixed restraint to the cover plate.

3.3.3.Materials of cover plate

By taking the tungsten alloy projectile impacting test on the confined SiC target[10]as reference,the influences of cover plate materials(steel,copper and aluminum)on interface defeat are discussed under the principles of equal thickness or areal density,respectively.The material parameters of copper and 4340 steel are given in Tables2 and 3,respectively.The 6061-T6 Al(Shock EOS and Steinberg Guinan Strength)in AUTODYN material library[22]along with the failure strain of 1.5 is adopted to model the dynamic response of aluminum.The simulated transition velocities for thecover plates having equal thickness or equal areal density are given in Table 6.It can be seen that,(i)when the thickness of cover plate is fixed,the transition velocity of 4340 steel is obviously higher than that of another two metallic materials,while there is little difference between the transition velocities of copper and aluminum cover plates;(ii)when the areal density of the cover plate is equal,the 4340 steel also leads to the highest transition velocity.The corresponding results of aluminum cover plate increase obviously attributed to its low est density and largest thickness,and the transition velocity of copper is the low est due to its largest density and least yield strength.Therefore,aiming to improve the impact resistance of ceramic composite target and increase the corresponding transition velocity,the 4340 steel is the optimal cover plate material based on the principles of either equal thickness or equal areal density,respectively.

Table 4 Simulated transition velocity with different projectile parameters.

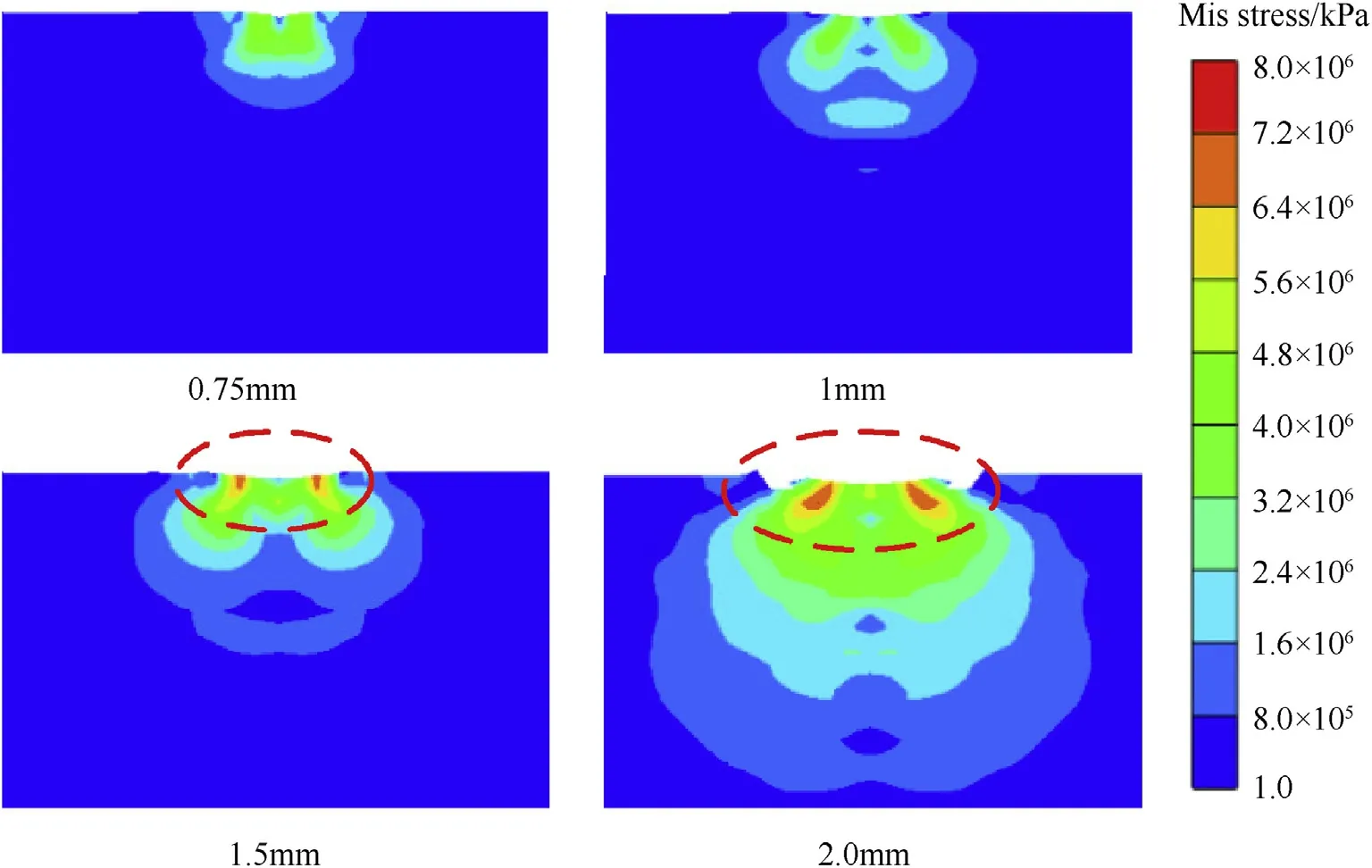
Fig.15.Von Mises stress in SiC ceramic targets subjected to the impact of pure gold projectiles with different diameters.

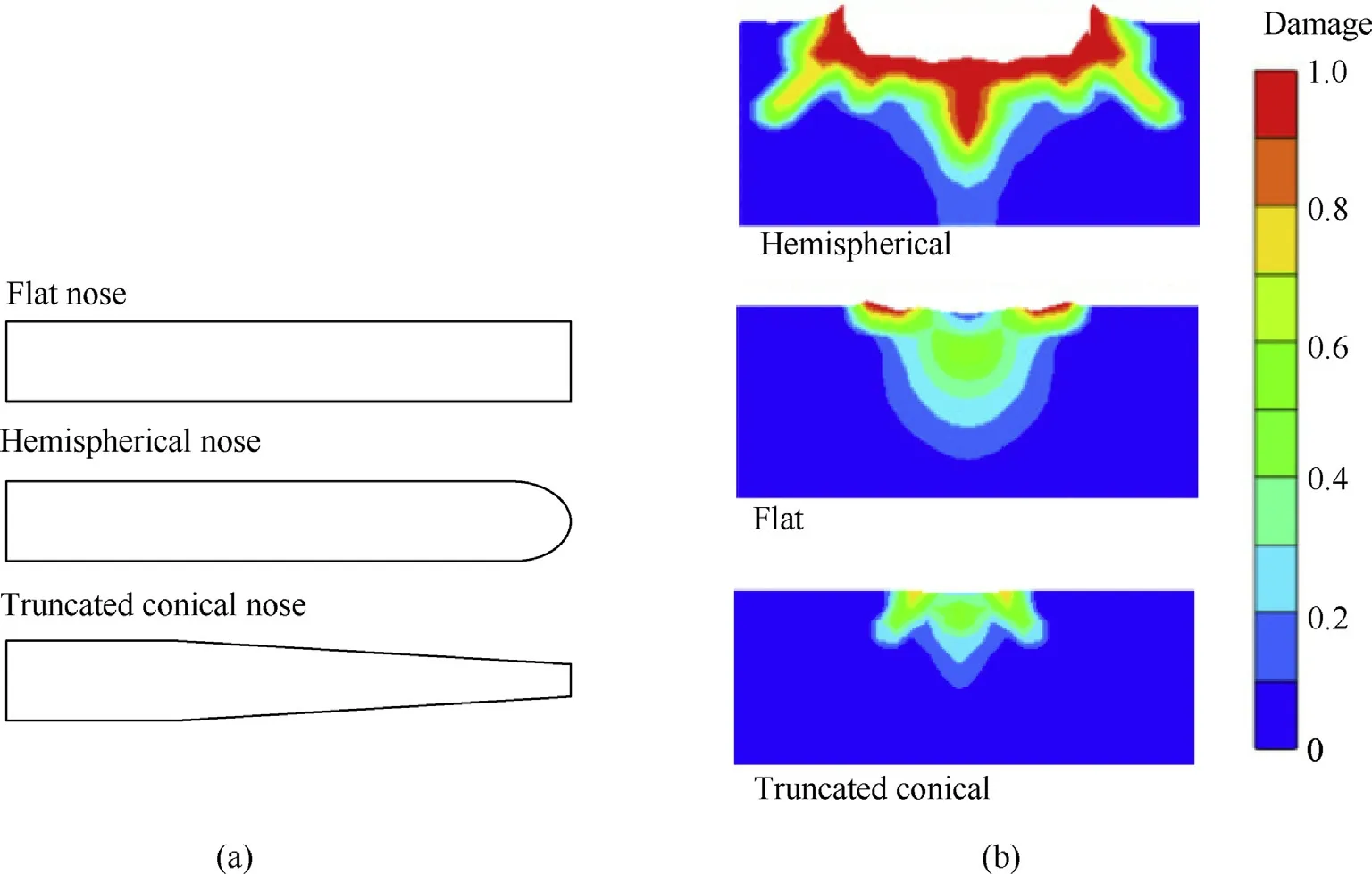
Fig.16.Pure gold projectile impacting on bare SiC ceramic target(a)schematic diagram of projectiles(b)damage distributions in targets.

3.4.Prestress on the ceramic target

Obvious enhancement of ballistic performance can be realized by attaching confinement to the ceramic target as well as imposing the prestress on it[34,35].By proposing a numerical method of applying the prestress on the ceramic target,the influence of various prestressing states(radial,axial and hydrostatic prestress)and different levels of prestress on the ballistic performance were studied by Holmquist and Johnson[17]and Chi et al.[21],respectively.Since the overall pressure due to the axial prestress in all cases and their differences are less than that for radial prestress[21],the influences of radial and hydrostatic prestress on the ballistic performance,especially on the dwell time are discussed in this section.

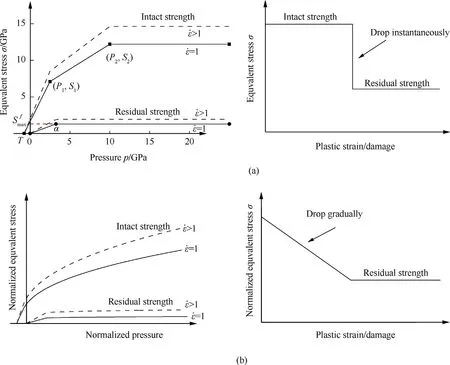
Fig.17.Strength models and strength-damage accumulation relationship of ceramic material in(a)JH-1 model(b)JH-2 model[20,30].

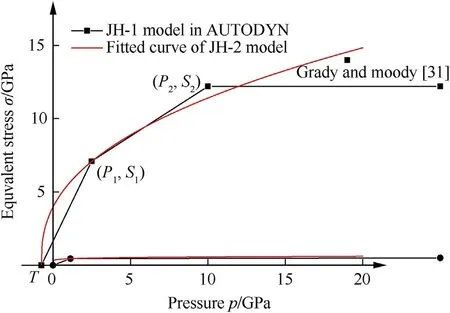
Fig.18.Yield surface of JH-1 and JH-2 models.

3.4.1.Numerical method of applying prestress on ceramic target

The tungsten alloy projectile impacting the confined SiC targets with striking velocities of 1645 m/s[11]is taken as the control test,and the geometry of the target is given in Fig.22(a)and Fig.22(b).The inner dimensions of the confinement(including the tube,the cover and back plates)are 20 mm in diameter and 20 mm in height,while the diameter D′and the height H′of the cylinder ceramic are varied to induce different stress states and prestress levels(see Fig.23).

Taking the radial prestress for example,the following steps are performed in order to impose the prestress on SiC target.Firstly,the target components including the tube and SiC ceramic are modeled in which the ceramic is slightly larger than the inner dimensions of the tube,it should be noted that no contact between the ceramic and the tube is defined in this step.Secondly,the boundary condition of a constant pressure or velocity is applied to the ceramicuntil the size of ceramic is slightly smaller than the tube,after that the boundary condition is removed and replaced by the fixed constraint.Besides,in this step,the edges of the ceramic which are perpendicular to the direction of the applied pressure or velocity are fixed,seen in Fig.22(c).Thirdly,the contact between the tube and ceramic is activated and all the boundary conditions on the ceramic are removed.The ceramic expands and comes into contact with the inner side of the tube,thus the prestress state is realized.More importantly,the static damping in AUTODYN[22]is utilized in this step to eliminate the stress oscillations and ensure a steady state of prestress.

Table 5 Parameters of JH-2 model for SiC ceramic.

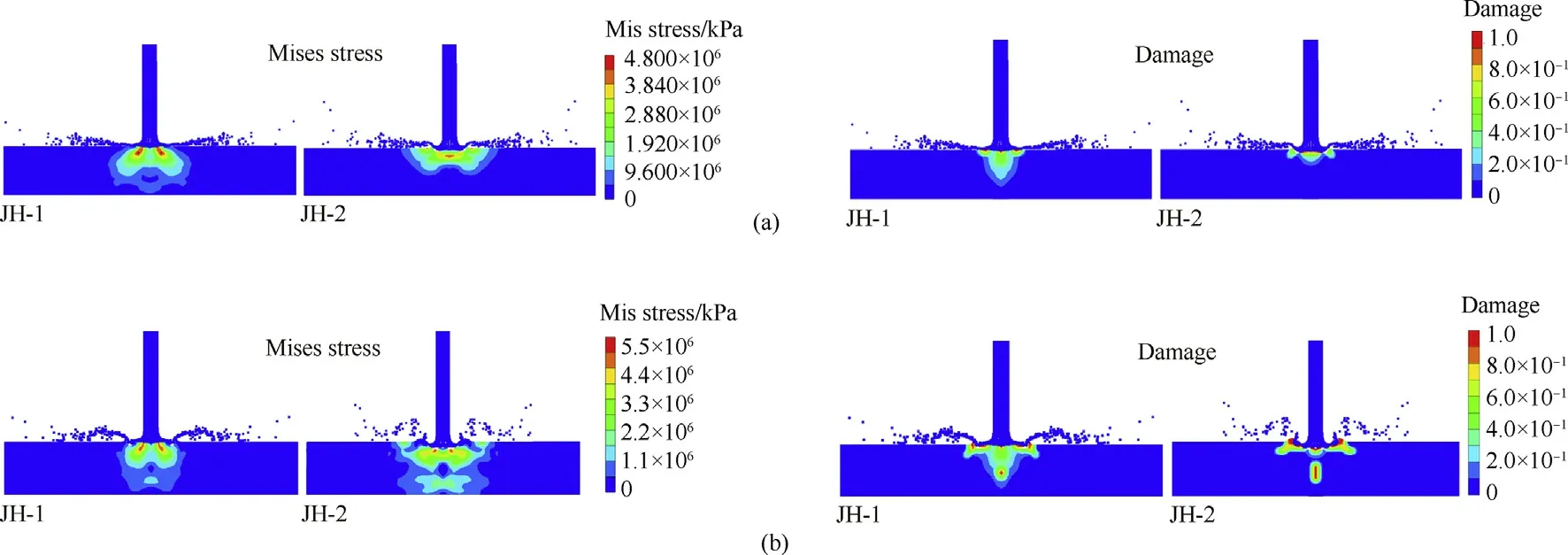
Fig.19.Distributions of Von Mises stress and damage in JH-1 and JH-2 models with striking velocities of(a)920 m/s(b)958 m/s.

Fig.20.Simulated DOP for different buffer thicknesses.

3.4.2.Radial and hydrostatic prestress on interface defeat

Follow ing the above procedure,different levels of radial(Rr=D′/20)and hydrostatic(Rh=H′/20)prestress on SiC ceramic are realized numerically,as shown in Fig.26.

Furthermore,the influences of different levels of radial and hydrostatic prestress on the interface defeat especially on the dwell time are discussed.The distributions of damage in ceramic targets with radial and hydrostatic prestress at the time instant of 16μs,as well as the corresponding DOP time-histories are shown in Fig.24 and Fig.25,respectively.It can be seen that,compared with the control test(Fig.9(b)),obvious enhancement of dwell of projectile is occurred when the radial or hydrostatic prestress is imposed on the SiC ceramic target.Meanwhile,the damage distributions in ceramic at the same time instant are all effectively reduced and become more concentrated with increasing the radial or hydrostatic prestress.Furthermore,within the given prestress levels(1≤Rr≤1.02,and 1≤Rh≤1.02),the dwell time of about 6μs derived numerically in Section 2.2 and Section 3.3.2 is prolonged monotonously with increasing the radial and hydrostatic prestress,and the influence of the hydrostatic prestress is more significant than that of the radial prestress.

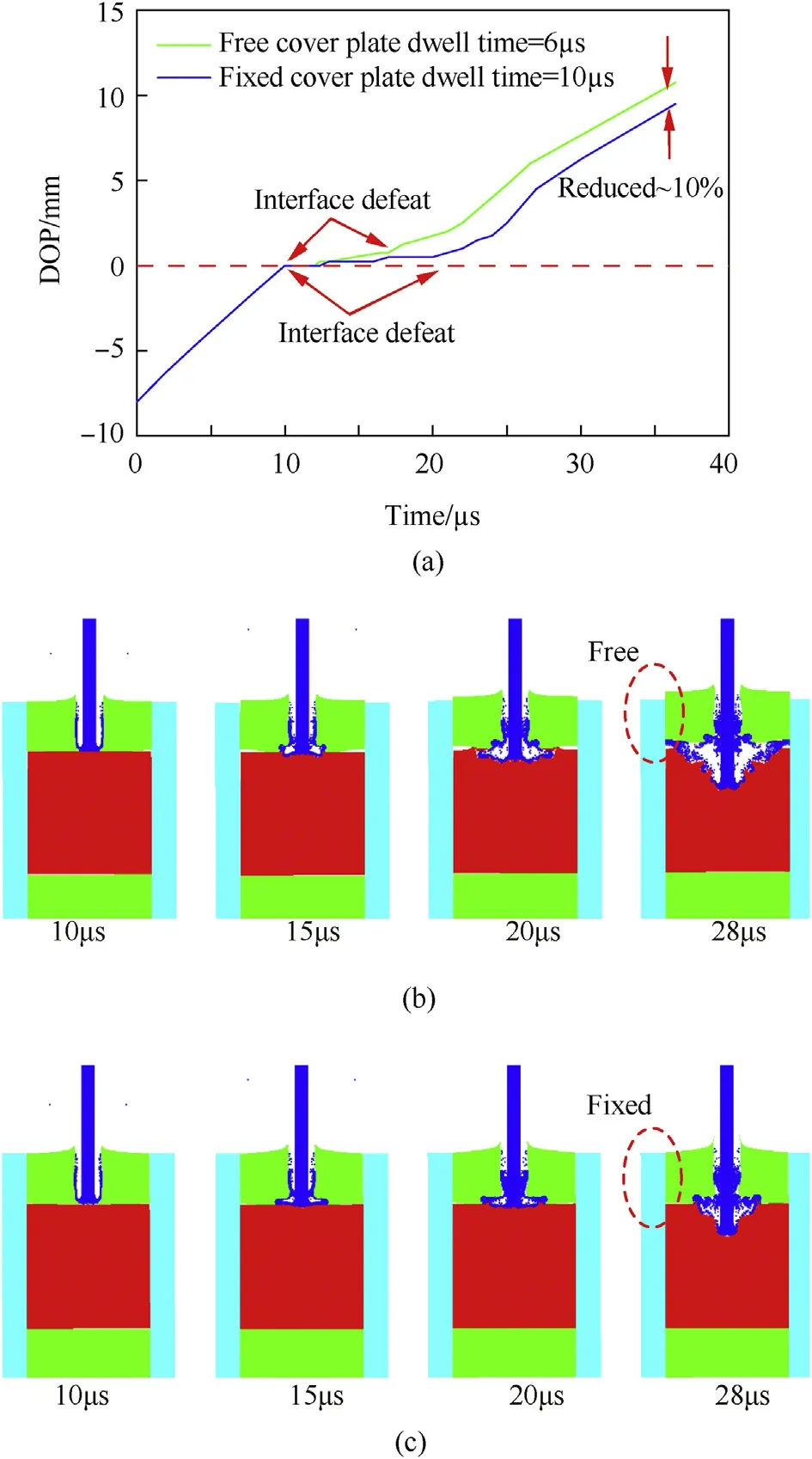
Fig.21.Comparisons for different constraints of cover plate(a)DOP(b)free cover plate(c)fixed cover plate.

Table 6 Simulated transition velocities for the cover plate with equal thickness and equal areal density.

Fig.22.Geometry of the target(a)tube,cover and back plates(b)ceramic(c)boundary condition during the prestress imposing process.

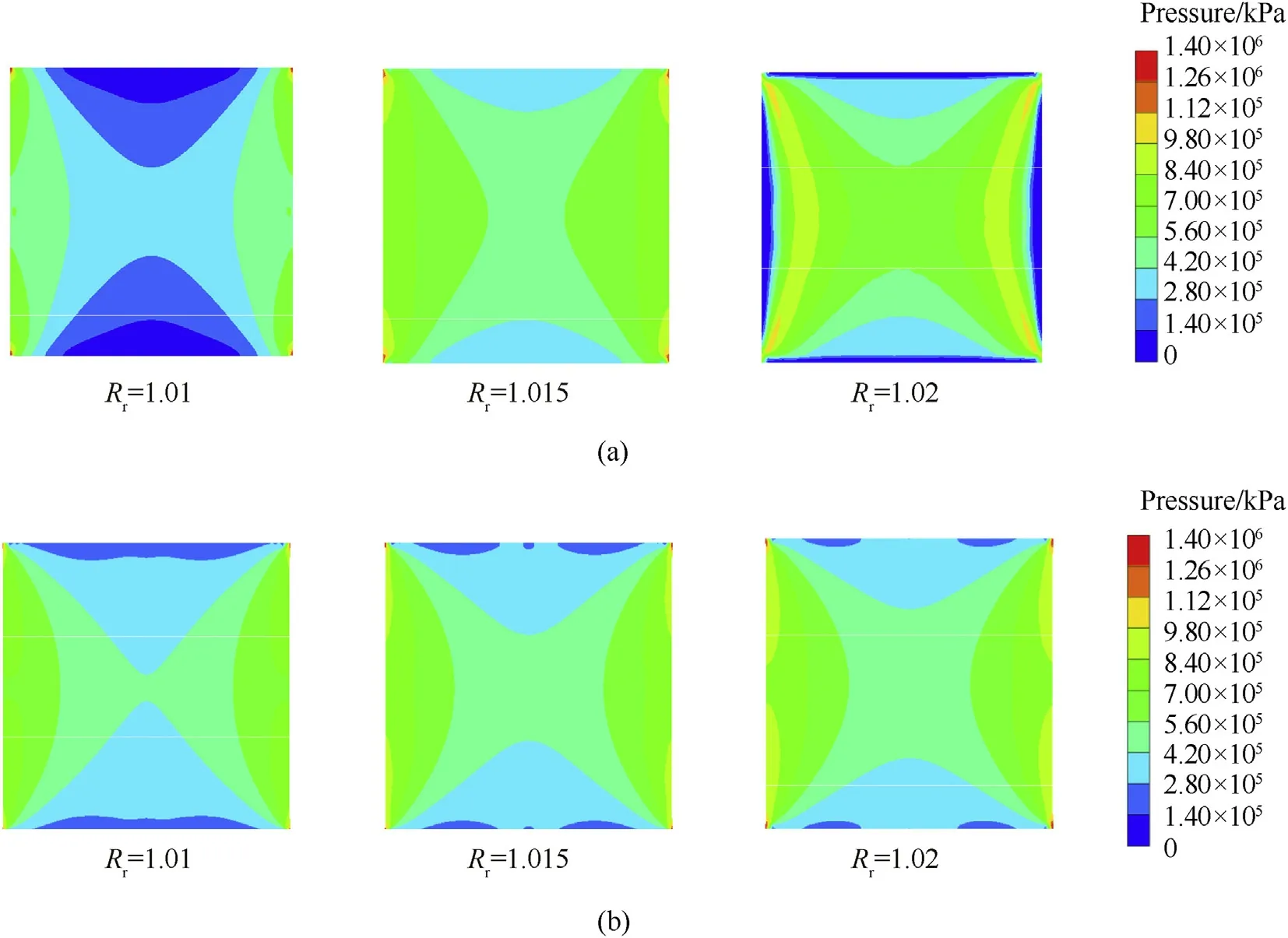
Fig.23.Different levels of(a)radial prestress(b)hydrostatic prestress on SiC ceramic.

4.A modified model to predict the upper bound of the transition velocity

4.1.Predictions of the transition velocity

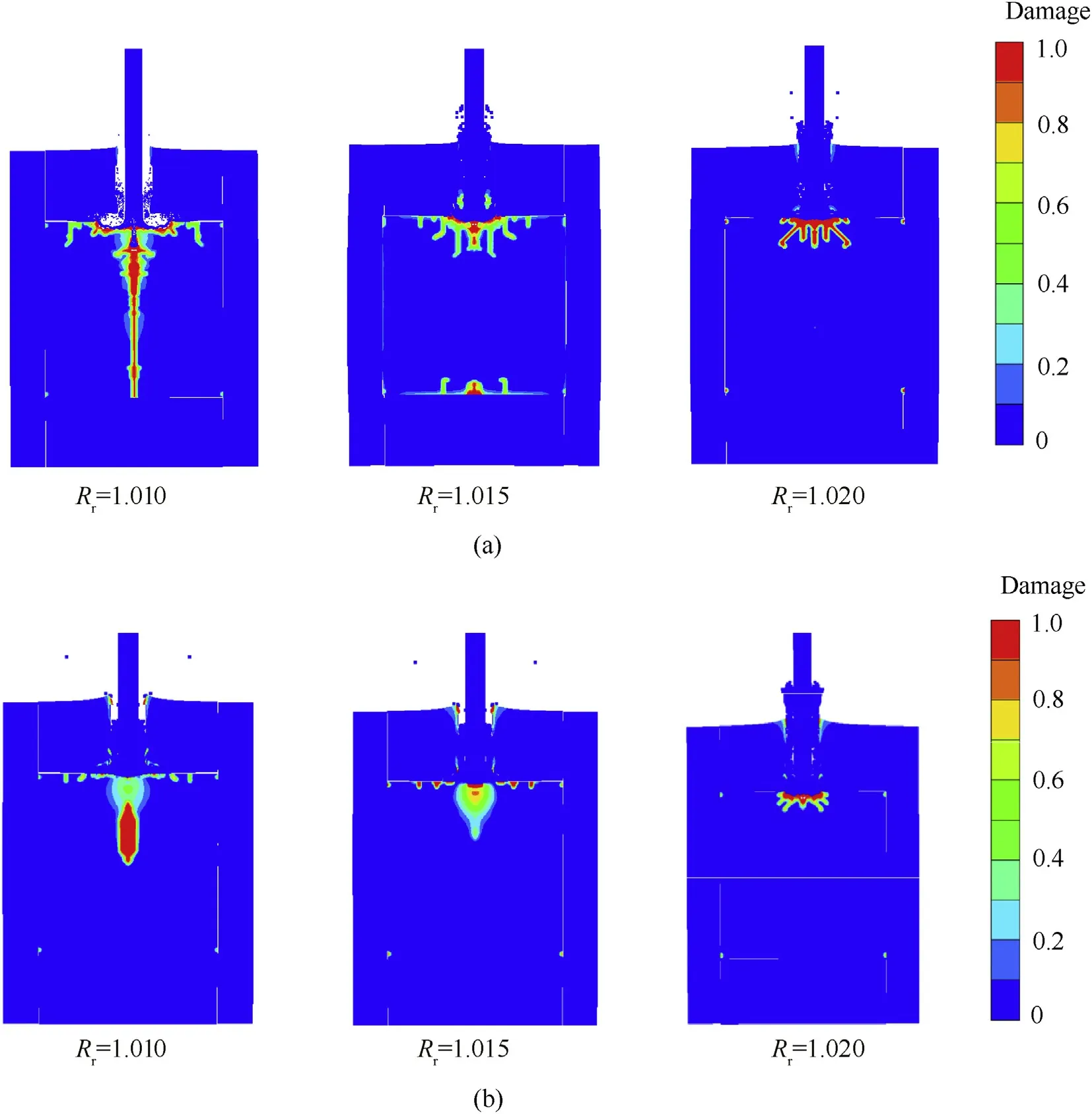
Fig.24.Distributions of damage in ceramic targets with the(a)radial prestress(b)hydrostatic prestress.

The approximate range of the pressure loading on the ceramic target corresponding to the dwell response from interface defeat to direct penetration was firstly proposed by Lundberg et al.[11]as

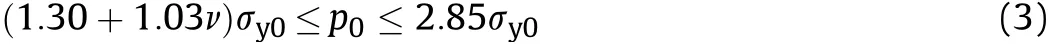
where

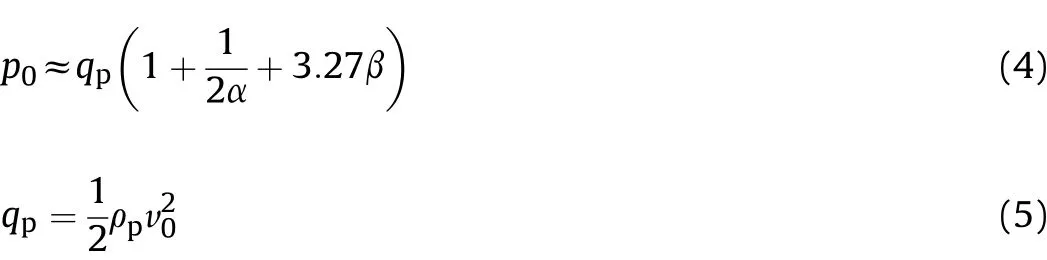
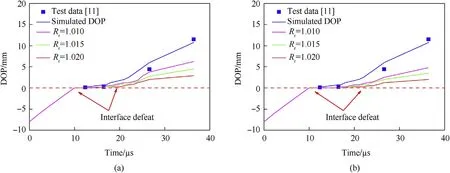
Fig.25.Influence of prestress on DOP(a)radial(b)hydrostatic.

Fig.26.Comparisons between experimental and theoretical transition velocities.

where ν and σy0are the Poisson's ratio and static yield strength of the ceramic material,respectively.qpis the stagnation pressure of an ideal fluid and v0is the impact velocity of projectile.Besides,the projectile is considered to be linearly elastic and perfectly plastic with the bulk modulus of Kp,yield strength of σypand density of ρp.Liet al.[26]proposed that the brittle ceramic can not withstand the plastic deformation and damage would occur when the impact induced pressure exceeds the HEL of the ceramic material.Therefore,it will be more reasonable to replace the lower bound of Eq.(3)with HEL,thus it has

By integrating Eq.(4)～Eq.(7)and ignoring the compressibility of the projectile material,i.e.,1/2α→0,the lower and upper bounds of the transition velocitywere further simplified by Li et al.[26]as

The transition velocities of tungsten alloy long-rod projectiles impacting nine different ceramic targets were experimentally obtained by Lundberg et al.[11]based on the reverse ballistic test,and the related parameters of ceramic targets are listed in Table 7.The comparisons between the theoretical predictions and experimental data are shown in Fig.26.It can be seen that,for the lower bound of the transition velocity,Li et al.[26](Eq.(8a))gives a satisfied prediction,while the corresponding results from Lundberg et al.[11](Eq.(3))are much lower than the test data.Besides,the predictions for the upper bound of the transition velocity proposed by Lundberg et al.[11](Eq.(3))and Li et al.[26](Eq.(8b))are both higher than the corresponding test results,thus the upper bound of the transition velocity is discussed in the next section.

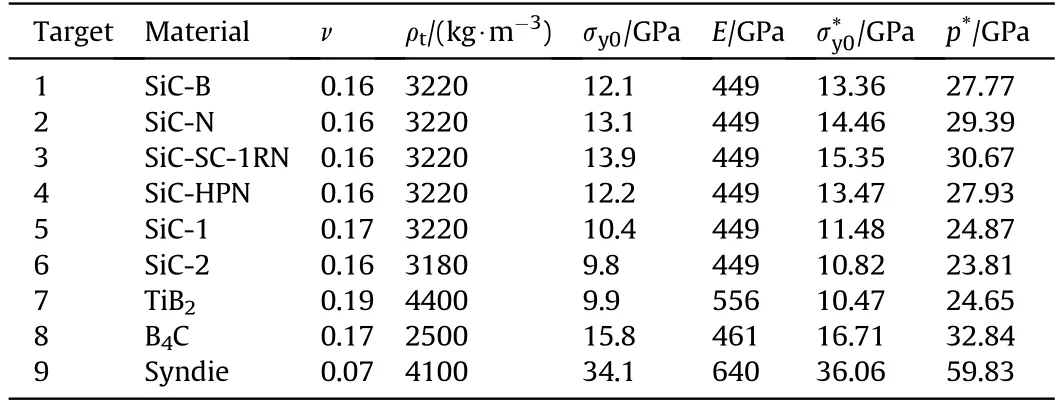
Table 7 Parameters of ceramics.

4.2.A modified model to predict the upper bound of the transition velocity

During the penetration process,a cylindrical cavity could be formed,which can be seen in both the experimental flash X-ray photograph[36]and the numerical simulation contour,as shown in Fig.27.

Based on the energy conservation approach,Hill and Mech[37]proposed the pressure required to form a cylindrical cavity on the surface of ceramic target without considering the strain rate effect

where E is the elastic modulus of the ceramic material.How ever,the strain rate effect(104～105s-1)of the ceramic target during the ultra-high speed(about 1500 m/s or more)penetration cannot be ignored.The yield strengththat considering the strain rate effect has been given in JH-1 and JH-2 constitutive models[20,30]for ceramic material as

Based on Eq.(10)and Eq.(11),the yield strength considering strain rate effect as well as the corresponding pressure required to form a cylindrical cavity on the surface of ceramic target can be calculated and listed in Table 7.It should be pointed out that the strain rate effect parameters of TiB2and Syndie are both assumed as 0.005.

In summary,the range of the pressure loading on the ceramic corresponding to the dw ell response from interface defeat to direct penetration can be further modified as

Fig.28 further shows the corresponding comparisons of the experimental and theoretical predicted upper bounds of transition velocities.It can be seen that the upper bounds of the transition velocity calculated from Eq.(12)are more close to the test data except for the SiC-2 ceramic target(target material No.6).Therefore,the correctness and applicability of Eq.(12)are validated,which can be adopted to predict the transition velocities for different combinations of projectiles and ceramic targets.

5.Conclusion

Fig.27.Direct penetration(a)flash X-ray photograph[36](b)numerical simulation contour.

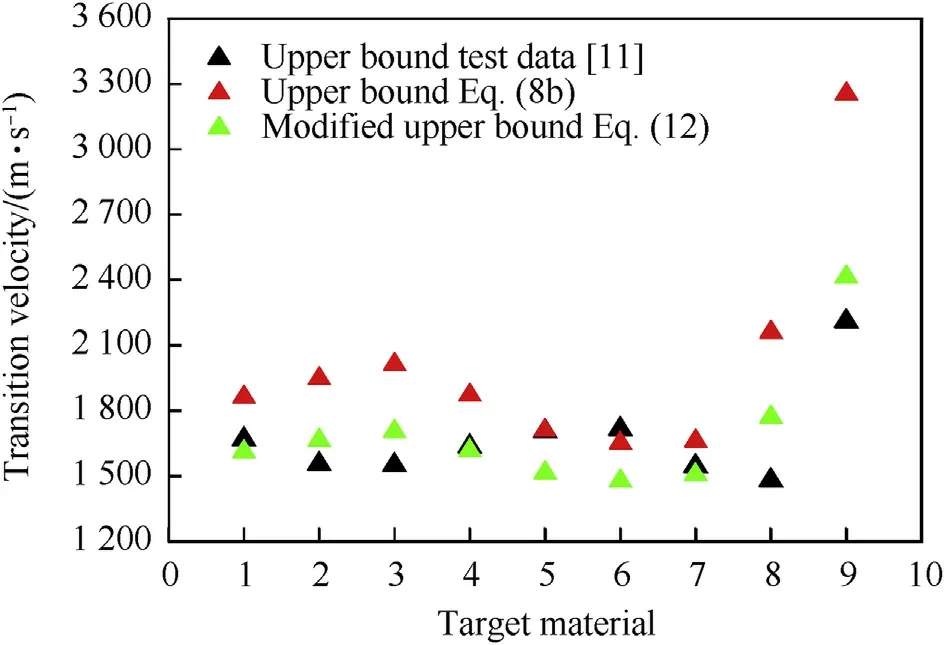
Fig.28.Comparisons between the experimental and theoretical upper bounds of the transition velocities.

Interface defeat phenomenon always occur when a long-rod projectile high-speed impacting on the ceramic target,which is studied numerically and theoretically in this paper.By respectively modeling the projectiles and ceramic targets with the SPH particles and Lagrange finite elements,the numerical algorithms,constitutive models and related material parameters are validated by comparing with the existing large amounts of test data.Three different responses,i.e.,complete interface defeat,dwell and direct penetration,are reproduced in different types of ceramic targets.The parametric studies are further carried out and it indicates that(i)the transition velocity of pure gold projectile is the highest compared with the tungsten and molybdenum projectiles,the lower bound of transition velocity decreases gradually with increasing the projectile diameter and can be significantly increased by truncated conical nose;(ii)JH-1 model is more suitable to describe the response of complete and partial interface defeat compared with JH-2 model;(iii)the dwell time cannot be prolonged monotonously with increasing the buffer thickness,while the damage area and penetration depth can be reduced effectively by applying constraints to the cover plates;(iv)compared with copper and aluminum,the 4340 steel is the optimal cover plate material based on the principles of either equal thickness or equal areal density;(v)obvious enhancement of ballistic performance can be realized by applying prestress on ceramic targets,and the influence of the hydrostatic prestress is more significant than that of the radial prestress.Finally,based on the energy conservation approach and taking the strain rate effect into account,a modified model to predict the upper bound of transition velocity is proposed and validated.

Acknowledgment

The project was supported by the National Natural Science Foundation of China(51878507).