圆片下料并行遗传算法的设计与实现

曾志阳，陈 燕，王 珂

（广西大学计算机与电子信息学院，南宁530004）

0 引言

从板材中切割出所需的毛坯是下料问题的一个热门研究方向，下料方案的优化可提高板材的利用率，简化下料过程［1］。圆片的生产工艺通常分为两种：剪切下料和非剪切下料［2］。非剪切下料是将不同圆片在原板材或卷材上进行排样，用火焰切割或激光切割直接切割出来；剪切下料先将板材剪切成条状，每个条带只放置相同种类的圆片，再将所需圆片从条带上切割出来。

下料问题是NP 难组合优化问题［3］，采用穷举法和精确算法在求解该类问题时很难在有限的时间内得到最优解。因此，求解圆片下料问题的常用方法主要有启发式算法和智能算法等，其中遗传算法（Genetic Algorithm，GA）是典型的智能算法。文献［4-6］均采用启发式的方法求解：文献［4］中分别采用X 向和Y 向直切布局求解，从中选择较大利用率的单个方向的布局图进行下料；文献［5］中用顺序分组启发式的方法求解圆片种类多、需求量较少的圆片下料问题；文献［6］中利用主动生成余料的策略，结合价值校正的启发方法求解。而文献［7］中则采用自适应遗传模拟退火算法求解卷材的圆片非剪切下料问题。目前笔者尚未查询到针对圆片剪切下料的遗传算法进行讨论的文献，且大部分是应用在求解矩形件在板材上的下料问题［8-10］。

研究表明，启发式算法能快速得到一个可行解，但无法确定是否为最优解，甚至无法确定与最优解的差距有多大。遗传算法则具有良好的全局优化能力，但如果处理方法不当，也易发生早熟现象从而陷入局部最优的情况［11］。因此，本文考虑在遗传算法的框架中上引入启发式的求解方法，设计以下料方案的板材利用率作为GA 评价函数的并行遗传下料算法（Parallel Genetic Blanking Algorithm，PGBA），将下料方案作为个体，采用多线程的方式对多个子种群进行并行的遗传操作。每个子种群用启发式方法求解单张板材上的布局图以生成初始种群，再通过自适应的遗传操作，遗传的交叉和变异阶段也采用启发式方法产生新个体，再利用评价函数对个体进行评价，选择其中部分个体进入下一代的进化。如此循环直至达到设定的进化代数，最终获得一个较优的圆片下料方案。

1 下料问题描述及数学模型

设一次下料需要m 种圆片，第i（i=1，2，…，m）种的直径和初始需求量分别为di和bi；可用板材的长宽分别为L 和W。要求从可用板材中切割出需求的圆片以满足生产需求，同时要求消耗的板材最少。一个下料方案由一个或多个布局图组成，并确定其使用次数。假设有K 种布局图，每一种布局图对应的使用次数为xk，第k 种布局图包含的第i 种圆片的数量为aik。下料方案的整数规划模型如下所示：

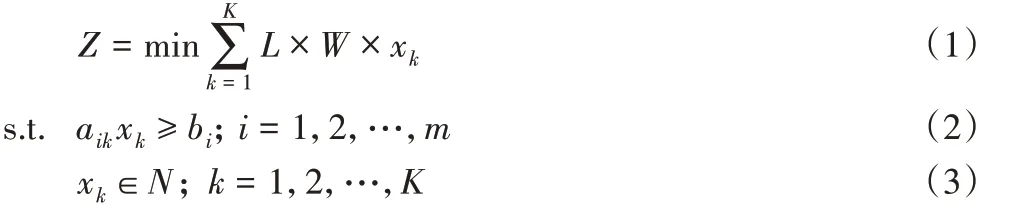
其中：式（1）为目标优化函数，目的是使消耗的板材数最少；式（2）表示下料方案中所有不同种类的圆片至少需要满足圆片的需求量；式（3）表示每种布局图的使用次数为非负整数。

1.1 圆片的布局

采用剪切工艺进行下料时，圆片在条带中的布局通常有并排、品排和斜排三种，当需求数大于10 时，采用品排布局的利用率优于其他两种布局［12］。生产中品排的布局通常不超过3 排，圆片在条带中的品排布局详细介绍可参文献［12］。令第i 种圆片在条带中布局有j(j=1，2，3)排，工艺余量为ω，对于m 种圆片，可枚举出M=3m 种宽度的条带，条带宽度wij可由式（4）计算，不同宽度条带所含第i 种圆片的个数zij可由式（5）计算。

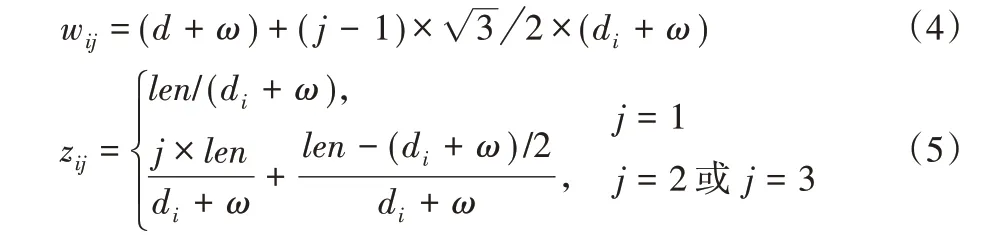
其中：di为第i 种圆片的直径，当圆片呈横向排列时，len=L，当圆片呈纵向排列时，len=W。

1.2 布局图的生成

根据文献［6］所述，条带的剪切工艺可分为滚剪和平剪两种方式，相对平剪方式，滚剪能大幅度减少条带切割的工作量，适合批量圆片的生成。滚剪通常采用直切布局图，其生成过程可看作条带沿X 方向或Y 方向的拼接过程，条带的长度或宽度均不超出板材的尺寸，不同方向的布局图如图1 所示。布局图的生成过程是背包问题的求解过程，目的是使得板材上放置的条带价值最大化，可用动态规划方法求解［13］。宽度为wij的条带的有效圆片数为其中l 为当前条带拼接方向的尺寸，条带的价值vij=cij⋅vi。设F(L，W)为板材的最大价值（布局图中有效圆片的总价值），F(x)为x×W 的子板材或L×y 的子板材的价值，其中1 ≤x ≤L，1 ≤y ≤W；η(l，i)记录子板材中第i种毛坯的数量。

用动态规划的递推方式生成布局图，递推式如下：

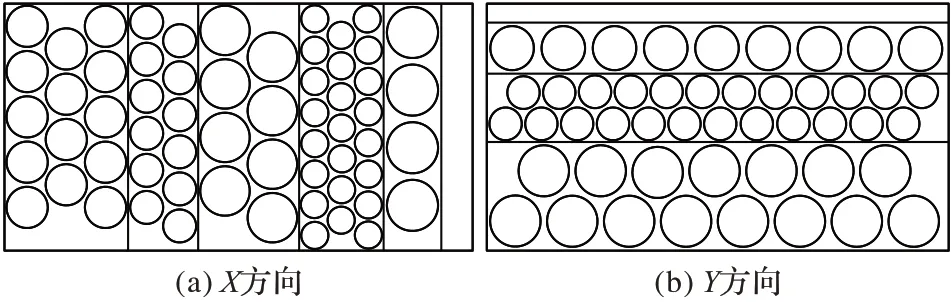
图1 X和Y方向的布局示意图Fig.1 Layout diagrams of X and Y directions

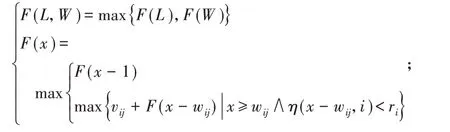
当布局为X方向，x=1，2，…，L，否则x=1，2，…，W （6）其中，F(0)=0，η(0，i)=0，i=1，2，…，m，j=1，2，3。

式（6）表明板材的最大价值取X 向和Y 向价值较大的布局图：当x=L 时，可确定所有F(L)的值；当x=W 时，可确定所有F(W)的值；最后取两者中的较大值作为F(L，W)。通过递推公式可得到布局图中所有条带的拼接情况以及所含的第i 种圆片的数量ni。确定当前布局图后，可根据式（7）计算布局图的使用次数xk，其中ri为毛坯的当前需求量。

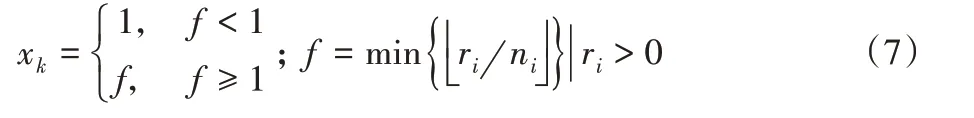
1.3 价值校正函数

用启发式方法生成初始种群个体的过程中，如果圆片的价值固定不变，根据动态规划的思想，每次生成的布局图都是不变的，并且在实际过程中发现，直径较小的圆片往往都会优先排入，导致后续的布局图中组合的效果较差。通过引入价值校正函数，调整每一种圆片的价值，能够有效降低算法的贪婪性，使得种群个体更加多样化［14］。本文采用的价值调整函数如下：

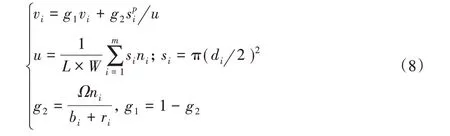
其中：si为第i 种圆片的面积，u 为当前布局图的利用率，ni为当前布局图中第i种圆片的个数，系数Ω=0.75，p=1.03。

2 并行遗传下料算法的设计

遗传算法具有隐式并行性，可方便进行并行的遗传操作，与串行遗传算法相比，可扩大搜索空间，获得更好的优化效果。并行遗传算法可通过分布式集群多处理器和单机多核处理器的多线程两种方式实现。本文采用后者进行并行遗传算法的设计来求解圆片的下料问题，通过粗粒度模型的并行模型设计并行遗传算法，将圆片的价值vi作为临界资源，各线程对临界资源进行互斥共享，每个线程内用启发式方法生成子种群，线程之间独立地进行自适应遗传操作，并通过一定的方式进行各子种群间的个体交流，提高算法的局部搜索能力，直至达到设定的最大进化代数R 后输出最优个体。并行遗传算法的线程范围为2～8 个线程，初始种群设定在[20，120]范围内，进化代数R设定在[20，100]范围内。

并行遗传算法Genetic()步骤如下：

步骤1 设定线程数T，种群的规模Q为T的正整数倍，最大进化代数R，输入板材尺寸L×W，毛坯种类数m，直径di，初始需求量bi。

步骤2 启用T 个线程，每个线程各自调用2.1 节的个体生成算法生成t=Q/T 个个体的子种群，初始化进化代数k=0，用σi(i=1，2，…，T)记录每个子种群进化过程中出现的适应度最高个体，用σbest记录最优的个体。

步骤3 计算各子种群计算个体的适应度Ui(i=1，2，…，t)，记录并更新适应度最高个体σi。

步骤4 令k=k+1，如果k ≤R，子种群内部进行选择、交叉和变异操作，然后判断每进化5 代后，将σbest迁移到其他子种群中，替换子种群内适应度最低的个体，转至步骤3；否则，线程结束，从σi中选择适应度最高的个体作为最优下料方案输出，算法结束。

2.1 编码方式及初始种群生成

设种群规模为Q，种群为(P1，P2，…，PQ)，其中一个个体代表一种下料方案，由于每个下料方案由一个或多个布局图和对应的使用次数组成，因此个体的基因由(pk，xk)组成，其中k=1，2，…，K，该编码方式有利于后续遗传操作和个体合法性的校正。

1）个体生成算法GetPlan()。

用启发式方法生成个体，具体步骤如下：

步骤1 令ri=bi记录毛坯当前剩余需求量，初始化k=0记录下料方案中布局图的种类数。

步骤2 如果存在任意的ri＞0，转至步骤3；否则，转至步骤4。

步骤3 令k=k+1，调用布局图生成算法生成布局图，将当前布局图记为pk，根据式（7）确定使用次数xk，将(pk，xk)记录成当前个体的一个基因，用ri=ri-xk×aik更新圆片剩余需求量，根据式（8）对圆片的价值vi进行调整，转至步骤2。

步骤4 令K=k 为当前个体的基因长度，得到初始种群的一个个体，算法结束。

2）布局图生成算法GetPattern()。

由式（4）计算出所有条带的宽度wij，由式（5）分别计算出X 方向条带的圆片数量zxij和Y 方向条带的圆片数量zyij，条带的价值分别为vxij和vyij，根据1.2节的递推式设计生成布局图的算法。具体步骤如下：

步骤1 令x=0 记录X 方向子板材长度，令y=0 记录Y方向子板材宽度。

步骤2 根据式（6）分别计算F(L)和F(W)，从而确定F(L，W)，再递推计算得出板材中所有条带的布局和所包含的各种圆片的总数ni。

步骤3 输出当前布局图，算法结束。

2.2 适应度函数

适应度函数用于评价个体的优劣。用个体对应的下料方案利用率（利用率=所需圆片总面积/消耗板材总面积）评价个体的适应度，利用率越大，说明个体的适应度越好。第i 个个体适应度Ui的计算公式为：

2.3 选择过程

选择过程是从当前的种群个体中选择部分个体进行后续的交叉变异等操作，适应度越高的个体被选择的概率越高。选择过程采用精英保留策略和轮盘赌选择策略，在保留适应度高的个体的同时保证个体的多样性。用式（9）计算每个个体的适应度，用精英保留策略将适应度最高的个体直接保留为选择后的个体之一，再用轮盘赌策略进行选择，直至达到当前种群的规模。选择后的个体进入交叉和变异过程。选择操作的具体步骤如下：

步骤1 计算个体适应度Ui(i=1，2，…，t)，选择其中适应度最高的个体为待交叉和变异个体之一。

步骤3 若k ≤t，转至步骤4；否则，转至步骤5。

步骤4 在[0，1]内产生一个随机数r，如果r ＜CP1，选择个体P1；否则，选择个体Pi，使得CPi-1＜r ＜CPi；令k=k+1，转至步骤3。

步骤5 输出选择后的所有个体，算法结束。

2.4 交叉过程

交叉过程是对两个个体的某些基因进行交叉，交叉后需对个体的合法性进行检验和校正，从而产生新的个体。交叉操作是避免遗传算法早熟的一个手段。本文采用两点双向交叉策略，自适应交叉概率pc的计算公式如下：

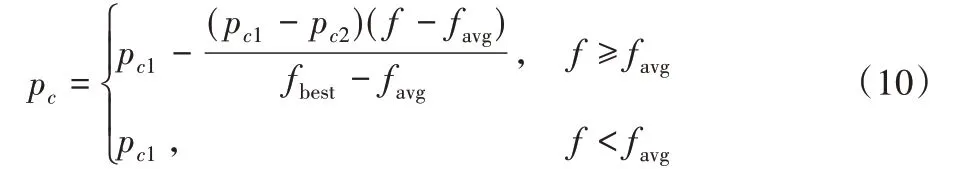
其中：f 为当前个体的适应度，fbest为子种群中最优个体的适应度，favg为子种群中所有个体的平均适应度；0 ＜pc2＜pc1＜1，本文中pc1=0.9，pc2=0.6。

由P1至Pt按顺序选择两个相邻个体，对于选择的两个个体，计算交叉概率pc，在[0，1]内产生一个随机数r，如果r ＜pc，则对这两个个体进行交叉；否则，进行下一次选择，直至所有个体选择完毕。假设选择交叉的两个个体为P1和P2，个体长度分别为K1和K2，具体的交叉过程如下：计算f=max{Uq1，Uq2}，根据式（10）计算pc，在[0，1]内产生一个随机数r。如果r ＜pc，在[1，min(K1，K2)]内产生两个不相等的随机整数a 和b，为避免无效交叉，交叉部分的基因段的长度不能等于个体的长度，因此a 和b 需满足：当a ＜b 时，b-a+1 ≠min(K1，K2)或当a ＞b 时a-b ＞1。若a ＜b，则将个体P1和P2的[a，b]区间的基因进行交换；若a ＞b，则将个体P1和P2的[1，b]区间的基因进行交换，再将P1的[a，K1]区间的基因和P2的[a，K2]进行交换。交叉结束后产生的新个体为P1'和。

用下面的例子说明具体的交叉过程：P1和P2的个体长度分别为K1=7和K2=6。假设产生的随机整数a=3，b=5，由于a ＜b，因 此 将P1的 基 因 段(q13，q14，q15)和P2的 基 因 段(q23，q24，q25)进行互换，互换过程如图2（a）所示。假设产生的随机整数a=5，b=2，由于a ＞b，因此将P1的基因段(q11，q12)和P2的 基 因 段(q21，q22)进 行 互 换，再 将P1的 基 因 段(q15，q16，q17)和P2的基因段(q25，q26)进行互换，互换过程如图2（b）所示。

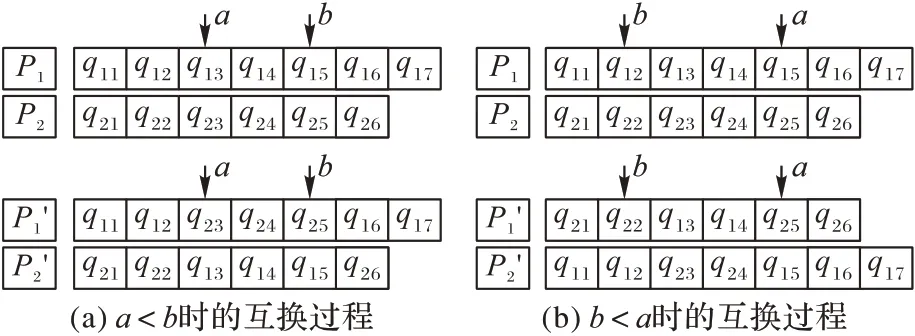
图2 两点双向交叉Fig.2 Crossover of two points and two directions

通过交叉生成的新个体由于其中的部分基因序列产生了变化，导致新个体中部分种类毛坯总数明显超出需求量，或者部分种类毛坯的需求量未得到满足，从而导致非合法个体的出现，因此交叉后要对新个体进行合法性检验和校正。具体算法步骤如下：

步骤1 令ri=bi以记录毛坯当前剩余需求量，K 为新个体基因长度，若a ＜b，转至步骤2；若a ＞b，转至步骤4。

步骤2 保留[1，a-1]和[b+1，K]区间的基因，并根据相应的(pk，xk)，用ri=ri-xk×aik更新圆片剩余需求量。

步骤3 遍历[a，b]的每一个新基因(pk，xk)，若布局图pk中存在已满足需求的毛坯，舍弃该基因，令K=K-1；否则，保留当前布局图pk，根据式（7）重新确定使用次数xk，用ri=ri-xk×aik更新圆片剩余需求量。遍历结束后，由前往后调整各基因的位置，转至步骤6。

步骤4 保留[a+1，b-1]区间的基因，并根据相应的(pk，xk)更新剩余需求量：ri=ri-xk×aik。

步骤5 遍历[1，b]和[a，K]的每一个基因(pk，xk)，若布局图pk中存在已满足需求的毛坯，舍弃该基因，令K=K-1；否则，保留当前布局图pk，根据式（7）重新确定使用次数xk，用ri=ri-xk×aik更新圆片当前剩余需求量。遍历结束，由前往后调整各基因的位置，转至步骤6。

步骤6 若存在任意的需求量ri＞0，转至步骤7；否则，转至步骤8。

步骤7 调用布局图生成算法生成一个布局图，令K=K+1，k=K，将当前布局图记为pk，并根据式（7）确定使用次数xk，将(pk，xk)记录成当前个体的一个基因，用ri=ri-xk×aik更新圆片剩余需求量，根据式（8）对圆片的价值vi进行调整，转至步骤6。

步骤8 输出校正后的个体，算法结束。

2.5 变异过程

变异过程是对个体的某些基因用新的基因替换，并保证变异过程中个体的合法性，从而产生一个新的个体。变异过程的目的有两个：一是使遗传算法具有局部的搜索能力；二是使遗传算法维持群体多样性，以防止出现早熟的现象。本文采用两点双向变异策略，自适应变异概率pm的计算公式如下：

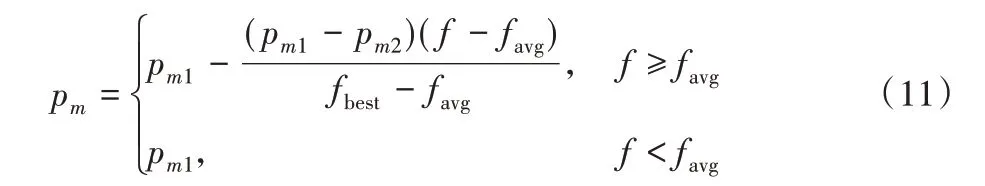
其中：f 为当前个体的适应度，fbest为种群中最优个体的适应度，favg为种群的平均适应度；0.02 ＜pm2＜pm1＜0.2，pm1=0.1，pm2=0.05。

由P1至Pt按顺序选择个体，对于当前选择个体，计算变异概率pm，在[0，1]内产生一个随机数r，如果r ＜pc，则对该个体进行变异；否则，进行下一次选择，直至所有个体选择完毕。具体的变异过程如下：假设选择的个体为P，个体长度为K，根据式（11）计算pm，在[0，1]内产生一个随机数r，若r ＜pm，在[1，K]内产生两个不相等的随机整数a 和b。若a ＜b，将[a，b]区间基因进行变异；若a ＞b，则将[1，b]，[a，K]的基因进行变异。变异后的新个体为P'。

用下面的例子说明具体的变异过程：P 的个体长度为K=7。假设产生的随机整数a=3，b=5，由于a ＜b，因此将基因段(q3，q4，q5)进行变异，变异过程如图3（a）所示；假设产生的随机整数a=6，b=2，由于a ＞b，因此将P 的基因段(q1，q2)和(q6，q7)进行变异，变异过程如图3（b）所示。

图3 两点双向变异Fig.3 Mutation of two points and two directions

在变异过程中，需要保证变异产生的新基因不包含已满足需求的毛坯，具体算法步骤如下：

步骤1 令ri=bi记录毛坯当前剩余需求量，K 为新个体的基因长度，若a ＜b，转至步骤2；若a ＞b，转至步骤3。

步骤2 将[a，b]的基因从个体中移除，令K=K-l为个体的基因长度，由前往后调整各基因的位置，转至步骤4。

步骤3 将[1，b]和[a，K]的基因从个体中移除，令K=K-l 更新个体的基因长度，由前往后调整各基因的位置，转至步骤4。

步骤4 遍历当前个体的每个基因，根据(pk，xk)用ri=ri-xk×aik更新圆片剩余需求量。

步骤5 若存在任意ri＞0，转至步骤6；否则，转至步骤7。

步骤6 调用布局图生成算法生成布局图，令K=K+1，令k=K，将当前布局图记为pk，并根据式（7）计算使用次数xk，将(pk，xk)记录成当前个体的一个基因，用ri=ri-xk×aik更新圆片剩余需求量，根据式（8）对圆片价值vi进行调整，转至步骤5。

步骤7 输出新的个体，算法结束。

3 实验结果及分析

PGBA 用C#语言编程实现，运行机器CPU 为i5-4590，主频3.30 GHz，四核四线程，内存16 GB。为与后续比较的一致性，板材尺寸设为L×W=2 000×1 000，工艺余量ω=5。根据文献［7］的分析，线程的数量增加有利于提高算法的运算性能，因此将算法的线程数设为T=4。实验首先对遗传算法的进化代数和种群规模两个参数进行测试，分析两者对算法的性能影响；再通过与串行遗传算法和相关文献算法进行比较分析，验证算法的有效性。

3.1 算法在不同参数条件的性能比较

在遗传算法中，种群规模和进化代数对算法的性能起到重要作用，一般来说，种群规模和进化代数越大，算法搜索到更优解的可能性越大，但同时计算开销也会增加，因此需要根据实际需求确定合适的参数范围。本节通过对算法不同参数进行测试，以确定合适的种群规模和进化代数。

1）不同进化代数的比较。

测试用例参照文献［6］的参数范围进行设定，相关参数取值范围如表1所示。根据表1生成300个随机测试算例。

表1 随机算例相关参数Tab.1 Relevant parameters for random examples

设种群规模Q=80，分别在进化代数10、20、50、100 的条件下进行测试，300 个算例在不同进化代数的材料平均利用率如图4 所示。可以看出，当R 较小时，随着进化代数的增加，平均利用率的提高速度较快，当R 达到50 代之后，平均利用率的提高速率减缓。同时，随着进化代数的增加，平均利用率有所提高，但运算时间也不断增加：当R=10 时，平均每个算例的计算时间为13.54 s；当R=100 时，平均计算时间达到了103.67 s。综合利用率和运算时间，设定算法的进化代数R=50。

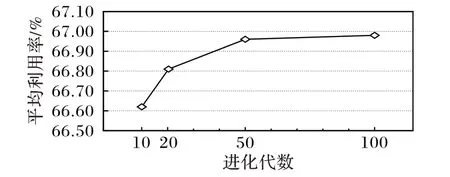
图4 不同进化代数的平均利用率Fig.4 Average utilization rate of different evolutionary generations

2）不同种群规模的比较。

设定进化代数R=50，用测试1）中300 个随机算例分别在种群规模为20、40、80、100、120 的条件下进行测试，结果如图5 所示。可以看出，随着种群的规模增大，300 个算例的平均材料利用率呈线性增加，当种群规模增加到80 个之后，平均利用率的提高速率减缓。并且随着种群规模的增大，算法的计算时间也会增加：当Q=20 时，平均计算时间为17.54 s；当Q=120 时，平均计算时间为83.24 s。因此设定种群的规模Q=80。

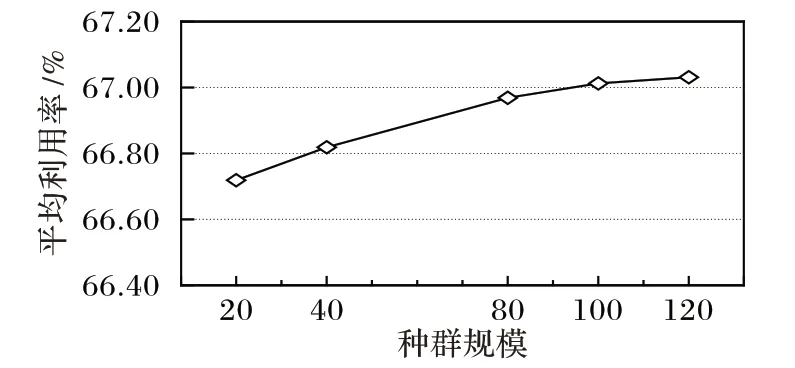
图5 不同种群规模的平均利用率Fig.5 Average utilization rate of different population sizes

3.2 与串行遗传算法的比较

3.1 节中产生的随机算例特点属于圆片需求种类少但需求量较大的情况。在下料的组合优化问题中，随着圆片的种类和需求量增加，问题的规模和求解难度也不断增大。本节根据表2 的相关参数范围，随机生成四组不同规模的算例，分别用并行遗传算法和串行遗传算法进行测试。

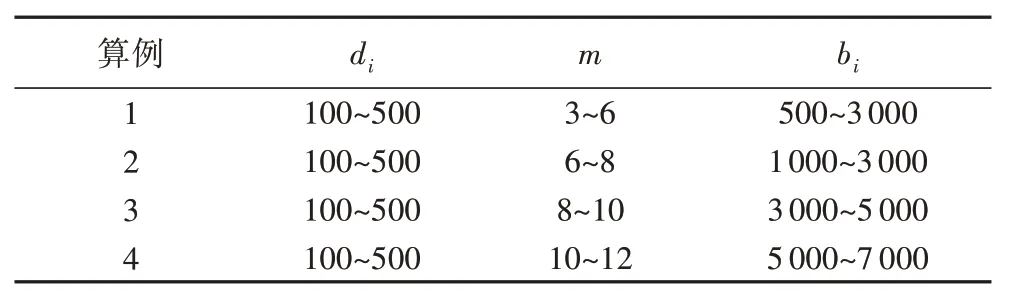
表2 不同规模算例参数设置Tab.2 Parameters setting for examples with different scales

不同规模的算例运行结果如表3 所示。可以看出：并行遗传算法与串行遗传算法在材料利用率上都得到了提高，可以有效缩短计算时间；并且随着问题规模的增加，并行遗传算法的计算速度更快，效果更明显。

表3 不同规模的算例运行结果比较Tab.3 Running results comparison of examples with different scales

3.3 与文献算法在材料平均利用率上的比较

文献［6］中针对圆片剪切下料问题，采用主动生成余料条带策略，用启发式方法求解下料方案，以提高一个周期内的总体的材料利用率，文献［6］的算例属于圆片种类数较少，但需求量较大的情况。

1）与文献［6］方法的比较。

针对文献［6］不主动产生余料的策略，用文献［6］中的30个算例对本文算法进行测试，结果如表4所示，其中30个算例的消耗板材总面积为S，材料平均利用率为UL，平均计算时间为T，Δ 则表示两个对比算法的参数结果差值。可以看出，文献［6］算法所消耗材料的总面积为35 388 m2，本文算法所消耗板材的总面积为33650 m2，相比之下节省板材面积1 738 m2，材料利用率提高3.21%，虽然运算时间增加较多，但仍在可接受范围内，并且材料利用率得到了较大的提高。

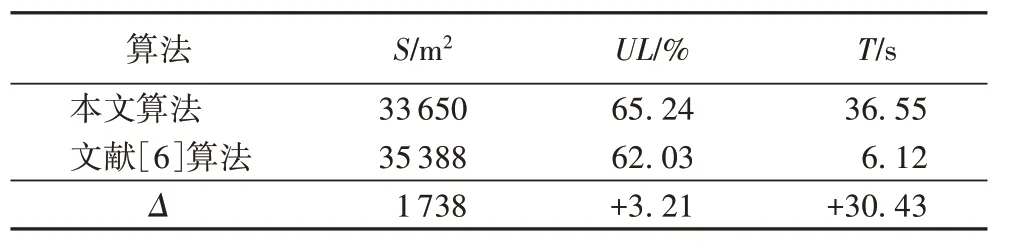
表4 两种算法的剪切下料结果比较Tab.4 Comparison of cutting results of two algorithms

2）更大规模问题的比较。

在3.3 节测试1）中，PGBA 对于文献［6］的算例取得了较好的测试效果，为了进一步验证PGBA 的有效性和适应性，根据表5随机生成30个更大规模问题的算例，相比文献［6］的算例，这30个算例的圆片种类数更多，需求量更大。

分别用本文算法和文献［6］算法和进行测试，两种算法的材料平均利用率如表6 所示。可以看出，30 个算例的材料平均利用率得到了提高，文献［6］算法所消耗材料的总面积为57 358 m2，本文算法所消耗板材的总面积为5 6313 m2，相比之下节省板材面积1 045 m2，总体材料利用率提高1.25%，计算时间在可接受的范围内。

表5 随机算例相关参数Tab.5 Relevant parameters of random examples

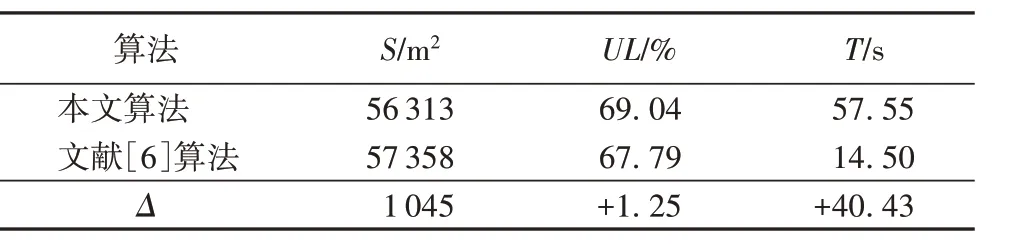
表6 两种算法在大规模问题算例上的剪切下料结果比较Tab.6 Comparison of cutting results of two algorithms for large-scale examples

实验结果表明，本文算法对于不同规模问题都能取得较好的效果，虽然计算时间增加，但在实际生产中，花费较多的计算时间来获得利用率的提高是可以接受的。

4 结语

本文针对圆片直切布局的下料问题提出了并行遗传下料算法PGBA。在并行遗传算法的基础上，对个体采用特定的编码方式，用启发式的方法生成初始种群，并通过性能较好的自适应遗传操作来提升算法的性能和效率。实验结果表明，

PGBA 具有良好的性能，可以在满足实际生产中对计算时间要求的情况下，使板材的利用率普遍达到或超过一般的启发式方法，在解决圆片剪切下料问题上具有良好的实用性。在今后的研究中，我们可以在PGBA 的基础上，从实际生产的需求出发，通过对算法的相关参数和采用的策略进行修正和测试分析，或是结合其他算法，进一步对下料问题的优化进行研究。