三次对称多项式x3+y3+z3-3xyz的因式分解及其应用(Ⅲ)

刘合国,高睿,徐行忠,雒晓良

(湖北大学数学与统计学学院, 湖北 武汉 430062)

0 引言

在文献[1-2]里, 我们从下面的恒等式出发:

x3+y3+z3-3xyz=(x+y+z)(x2+y2+z2-xy-yz-zx)

=(x+y+z)(x+ωy+ω2z)(x+ω2y+ωz),

这里ω是1的3次本原单位根, 处理了不少初等问题, 这个方法简捷易学.近来翻看柯斯特利金主编(丘维声译)的第4版《代数学习题集》, 其中P86的21题如下所示.

例1在复数域上解方程组

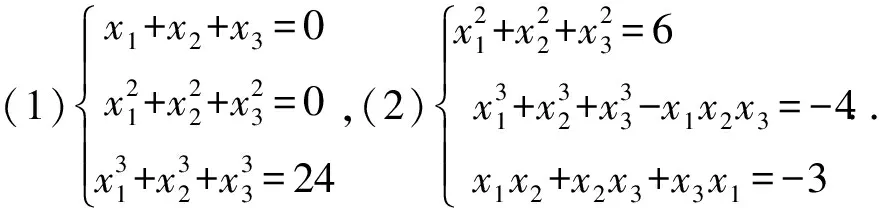
利用我们的技术, 可以很快求出这两个方程组的解.

解记σ1=x1+x2+x3,σ2=x1x2+x2x3+x3x1,σ3=x1x2x3.

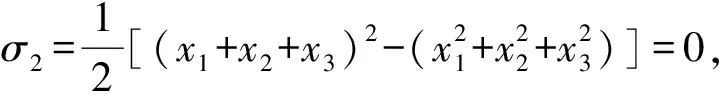
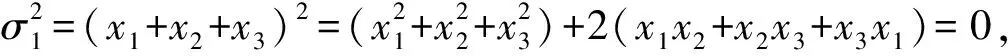
柯斯特利金是学术大家, 在代数学的广阔领域里具有精深的造诣, 是20世纪苏联、俄罗斯代数学方面的标志性人物之一.阅读《代数学习题集》的序言, 再联想到两本内容丰富、能够启发学生思维的习题集:[苏]法杰耶夫、索明斯基著《高等代数习题集》和[苏]普罗斯库烈柯夫著《线性代数习题集》, 深感苏联、俄罗斯在代数学教学方面具有伟大的传统, 其学者在群论的字问题、Burnside问题等超级难题上取得举世瞩目的成就, 绝对不是偶然.

1 化简和证明

我们知道,x1,x2,…,xn上的每个对称多项式都可由n个初等对称多项式

唯一地表达出来, 这是对称多项式的基本结果.在文献[1-2]里, 我们还没有运用过此结果, 现在补上若干实例, 作为它的应用.

例2证明

x3+y3+z3-3xyz=(x+y+z)3-3(x+y+z)(xy+yz+zx)=

(x+y+z)(x2+y2+z2-xy-yz-zx).

x3+y3+z3-3xyz=(x+y+z)3-3(x+y+z)(xy+yz+zx)=(x+y+z)(x2+y2+z2-xy-yz-zx).

例2再次证明了当x+y+z=0时,x3+y3+z3-3xyz=0.

例3设a+b+c+d=0, 证明a3+b3+c3+d3=3(abc+bcd+cda+dab).

例3的证明令σ1=a+b+c+d,σ2=ab+ac+ad+bc+bd+cd,σ3=abc+bcd+cda+dab,σ4=abcd.

证法1:有a+b+(c+d)=0, 故a3+b3+(c+d)3=3ab(c+d), 从而

a3+b3+c3+d3=a3+b3+(c+d)3-3cd(c+d)=3ab(c+d)-3cd(c+d)=3ab(c+d)+3cd(a+b)=3(abc+bcd+cda+dab).

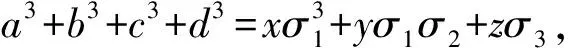
证法3:若abcd=0, 不妨设d=0, 则a+b+c=0, 有a3+b3+c3=3abc, 结论成立.

若abcd≠0, 有(x-a)(x-b)(x-c)(x-d)=x4+σ2x2-σ3x+σ4.分别令x=a,b,c,d代入并化简得

左右两边分别相加并整理即得a3+b3+c3+d3=3(abc+bcd+cda+dab).

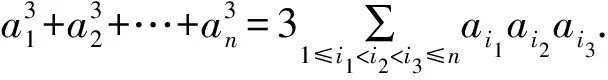
例4的证明证法1：利用对n的归纳进行证明.当n=3时结论成立.

假设n=k时结论成立, 下面我们来证明当n=k+1时结论也成立.

因a1+a2+…+(ak+ak+1)=0, 故由归纳假设有

从而

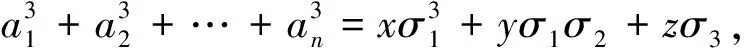
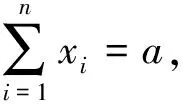
例6设u=x+y+z+a(y+z-2x),v=x+y+z+a(z+x-2y),w=x+y+z+a(x+y-2z), 证明u3+v3+w3-3uvw=27a2(x3+y3+z3-3xyz).

例6的证明注意到u+v+w=3(x+y+z)且uv+vw+wu=3(x+y+z)2-3a2(x2+y2+z2-xy-yz-zx), 从而

u3+v3+w3-3uvw=(u+v+w)3-3(u+v+w)(uv+vw+wu)=27(x+y+z)3-9(x+y+z)[3(x+y+z)2-3a2(x2+y2+z2-xy-yz-zx)]=27a2(x+y+z)(x2+y2+z2-xy-yz-zx)=27a2(x3+y3+z3-3xyz).

例7设a+b+c+d=0,证明a4+b4+c4+d4=2(ab-cd)2+2(ac-bd)2+2(ad-bc)2+4abcd.

左右两边分别相加并整理即得a4+b4+c4+d4+(a2+b2+c2+d2)σ2+4σ4=0.从而

例8证明 (a-b)6+(b-c)6+(c-b)6-9(a-b)2(b-c)2(c-a)2=

2(a-b)3(a-c)3+2(b-c)3(b-a)3+2(c-a)3(c-b)3.

例8的证明由于(a-b)+(b-c)+(c-a)=0,故(a-b)3+(b-c)3+(c-a)3=3(a-b)(b-c)(c-a), 左右同时平方并移项即得结论.

解由a+b+c=0, 知a3+b3+c3=3abc且a2+b2+c2=(a+b+c)2-2(ab+bc+ca)=-2(ab+bc+ca), 此时

例10设x,y,z是非零实数, 求k, 使(x+y+z)|x5+y5+z5-k(x2+y2+z2)(x3+y3+z3).

解由于(x+y+z)|x5+y5+z5-k(x2+y2+z2)(x3+y3+z3), 则x+y+z=0时,x5+y5+z5-k(x2+y2+z2)(x3+y3+z3)=0.由x+y+z=0, 知x3+y3+z3=3xyz且x2+y2+z2=(x+y+z)2-2(xy+yz+zx)=-2(xy+yz+zx), 此时

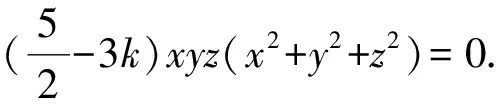
例11设a,b,c∈R,(a+b)(b+c)(c+a)≠0, 证明

例11的证明设f=(a+b+c)5-(a5+b5+c5), 因为f|a=-b=0, 所以a+b|f.同理b+c|f和c+a|f, 即(a+b)(b+c)(c+a)|f, 比较次数知可设(a+b+c)5-a5-b5-c5=(a+b)(b+c)(c+a)[m·(a+b+c)2+n(ab+bc+ca)], 其中m,n是实数.

令a=1,b=1,c=0, 得15=4m+n, 令a=0,b=1,c=2, 得35=9m+2n, 从而解得m=5,n=-5, 因此(a+b+c)5-(a5+b5+c5)=5(a+b)(b+c)(c+a)[(a+b+c)2-(ab+bc+ca)].另外(a+b+c)3-(a3+b3+c3)=3(a+b)(b+c)(c+a), 从而

子带内误差源于系统的非理想特性，发射机发射的信号经过接收机后，信号不再是理想的，出现了一定程度的失真，图2是单子带定标信号脉冲压缩结果。从图中可以看出信号出现了明显的畸变，旁瓣很高且不对称，必须进行补偿。

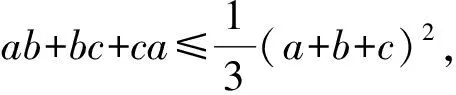
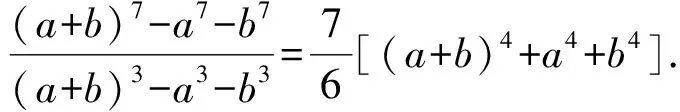
例12的证明有

(a+b)7-a7-b7=[(a+b)3-a3-b3][(a+b)4+a4+b4]+

ab(a+b)[a2(a+b)2+b2(a+b)2+a2b2]=[(a+b)3-a3-b3][(a+b)4+a4+b4]-[(a+b)3(a4+b4-a3(a+b)-b3(a+b))-a3b3(a+b)]=[(a+b)3-a3-b3][(a+b)4+a4+b4]+ab(a+b)[(a+b)2-ab]2

由于(a+b)-a-b=0, 故(a+b)3-a3-b3=3ab(a+b).又0=[(a+b)-a-b]2=(a+b)2+a2+b2+2[-(a+b)2+ab], 从而4[(a+b)2-ab]2=[(a+b)2+a2+b2]2=(a+b)4+a4+b4+2[(a+b)2-ab]2, 即2[(a+b)2-ab]2=(a+b)4+a4+b4.故

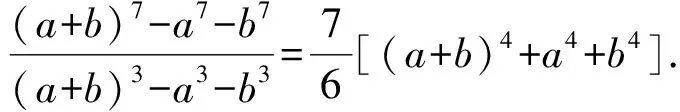
例13分解x3+y3+z3+t3-3(xyz+yzt+ztx+txy).

解x3+y3+z3+t3-3(xyz+yzt+ztx+txy)=x3+y3+(z+t)3-3(xyz+yzt+ztx+txy)-

3zt(z+t)=x3+y3+(z+t)3-3xy(z+t)-3zt(x+y+z+t)=(x+y+z+t)3-

3(x+y+z+t)(xy+xz+xt+yz+yt)-3zt(x+y+z+t)=(x+y+z+t)[(x+y+z+t)2-

3(xy+xz+xt+yz+yt+zt)]=(x+y+z+t)[x2+y2+z2+t2-(xy+xz+xt+yz+yt+zt)].

例14证明33n(33n+1)+33n+1-1不是素数.

例14的证明33n(33n+1)+33n+1-1=93n+33n-1+33n+1=

(93n-1)3+(33n-1)3-1+3·93n-133n-1=

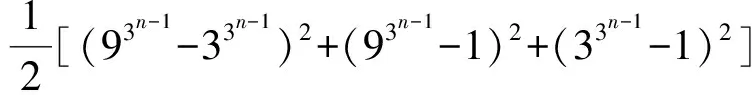
例15化简(x1+x2+x3)3-(x1+x2-x3)3-(x2+x3-x1)3-(x3+x1-x2)3.

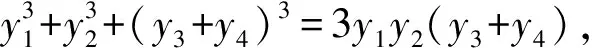
解法二设原式=a(x1+x2+x3)3+b(x1+x2+x3)(x1x2+x2x3+x3x1)+cx1x2x3, 令x1=1,x2=x3=0, 得a=0; 令x1=x2=1,x3=0, 得b=0; 令x1=x2=x3=1, 得c=24.

解法三记f(x1,x2,x3)=(x1+x2+x3)3-(x1+x2-x3)3-(x2+x3-x1)3-(x3+x1-x2)3.当x1=0时,f(0,x2,x3)=0, 故x1|f(x1,x2,x3); 当x2=0时,f(x1,0,x3)=0, 故x2|f(x1,x2,x3); 当x3=0时,f(x1,x2,0)=0, 故x3|f(x1,x2,x3); 从而x1x2x3|f(x1,x2,x3).此时比较次数可设f(x1,x2,x3)=kx1x2x3, 以x1=x2=x3=1代入即得k=24.

例16设x+y+z=xy+yz+zx=0, 证明(x3+y3+z3)2=3(x3y3+y3z3+z3x3).

解由x+y+z=0, 知x3+y3+z3=3xyz.又因为xy+yz+zx=0, 从而3(x3y3+y3z3+z3x3)=3[(xy)3+(yz)3+(zx)3]=9(xy)(yz)(zx)=(3xyz)2=(x3+y3+z3)2.

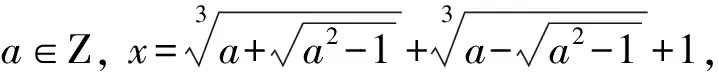
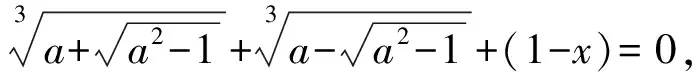
整理化简得x3-3x2=2a-2, 注意到a∈Z, 因此x3-3x2∈Z.

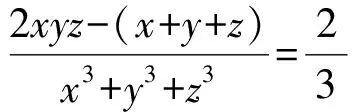
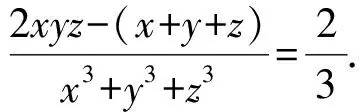
6xyz-3(x+y+z)=2[(x3+y3+z3)-3xyz+3xyz]=(x+y+z)[(x-y)2+(y-z)2+(z-x)2]+6xyz,

整理得(x+y+z)[(x-y)2+(y-z)2+(z-x)2+3]=0, 由于x,y,z∈R, 故(x-y)2+(y-z)2+(z-x)2+3>0, 故x+y+z=0.

例19设a,b,c∈Z, 6|a+b+c, 证明6|a3+b3+c3.

例19的证明有a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ca), 由于6|a+b+c, 所以a,b,c中至少有一个是偶数, 从而2|abc, 得6|3abc, 故6|a3+b3+c3.

例20(1)设A是一个3阶方阵, trA=0, 证明tr(A3)=3detA.

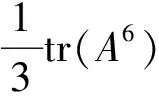
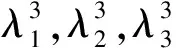
法二: 由Cayley-Hamilton定理得A3-trA·A2+α·A-detA·I=0, 移项得A3=trA·A2-α·A+detA·I, 两边取迹得tr(A3)=trA·tr(A2)-α·trA+3detA, 而trA=0, 故tr(A3)=3detA.

例21设a,b∈R,a3+b3=108,ab=6, 求a+b.

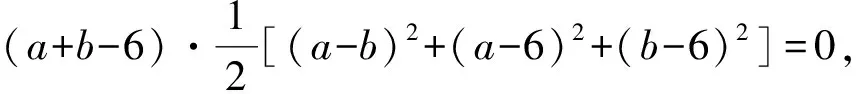
解法2:设a+b=x, 则a+b-x=0, 故a3+b3-x3+3abx=0, 代入条件化简得(x-6)[(x+3)2+9]=0, 由于a,b∈R, 故a+b=x=6.

解法3:有a3+b3=(a+b)[(a+b)2-3ab], 代入条件得(a+b)[(a+b)2-18]=108, 分解得(a+b-6)[(a+b+3)2+9]=0, 由于a,b∈R, 故a+b=6.

例22证明(a+b+c)3-[(a+b)3+(b+c)3+(c+a)3]+(a3+b3+c3)=6abc.

例22的证明有(a+b+c)3-(a3+b3+c3)=3(a+b)(b+c)(c+a),(a+b)3+(b+c)3+(c+a)3=3(a+b)(b+c)(c+a)+(a+b+c)[(a-b)2+(b-c)2+(c-a)2], 从而

2 结合韦达定理的应用

设x1,x2,…,xn是xn+a1xn-1+…+an=0的n个根, 韦达定理断言:

把本文中的技术与韦达定理结合起来, 能够很顺利地解决一些看似棘手的问题.

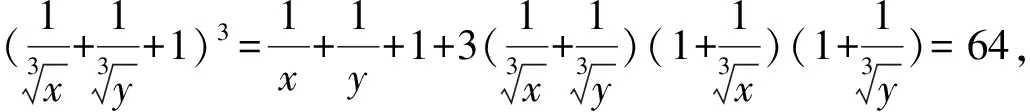
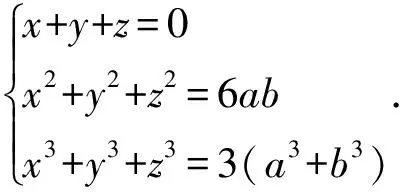
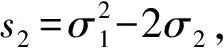
例25设x3-5x+a=0有两个根x1,x2满足x1+x2=2x1x2, 求a并解方程.

解设另一个根为x3, 则x1+x2+x3=0,x1x2+x2x3+x3x1=-5,x1x2x3=-a, 此时

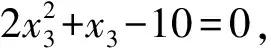
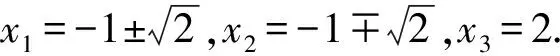
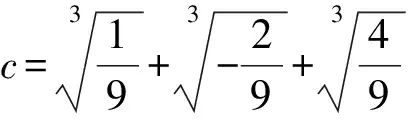
又因

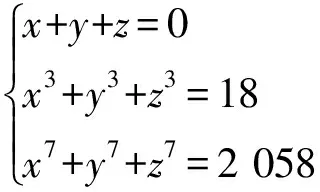
解设x,y,z是方程t3-σ1t2+σ2t-σ3=0的3个实根, 令si=xi+yi+zi,i=1,2,3.由x+y+z=0, 有x3+y3+z3=3xyz, 得σ3=6, 又

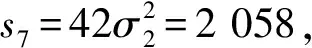
当σ2=7时,x,y,z是方程t3+7t-6=0的3个根, 由于(t3+7t-6)′=3t2+7>0, 即该方程仅有一个实数解, 从而原方程组无实数解.

当σ2=-7时,x,y,z是方程t3-7t-6=0的3个根, 分解得(t+1)(t+2)(t-3)=0, 从而得到原方程组的解为-1,-2,3.

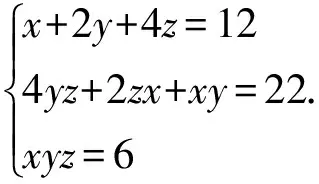
例29设α,β,γ是x3+ax2+bx+c=0的根, 求方程使得其根为

(1)α+β,β+γ,γ+α;

(2)α(β+γ),β(γ+α),γ(α+β).

解由韦达定理有

故

α2+β2+γ2=(α+β+γ)2-2(αβ+βγ+γα)=a2-2b,

且

α3+β3+γ3=(α+β+γ)[(α+β+γ)2-3(αβ+βa+γα)]+3αβγ=-a3+3ab-3c.

(1)有(α+β)+(β+γ)+(γ+α)=2(α+β+γ)=-2a.由

2[(α+β)(β+γ)+(β+γ)(γ+α)+(γ+α)(α+β)]=

=[(α+β)+(β+γ)+(γ+α)]2-(α+β)2-(β+γ)2-(γ+α)2

=[(α+β)+(β+γ)+(γ+α)]2-2(α2+β2+γ2)-2(αβ+βγ+γα),

可得

(α+β)(β+γ)+(β+γ)(γ+α)+(γ+α)(α+β)=a2+b.

又由(α+β+γ)3-(α3+β3+γ3)=3(α+β)(β+γ)(γ+α), 可得

(α+β)(β+γ)(γ+α)=c-ab.

从而根为α+β,β+γ,γ+α的方程为x3+2ax2+(a2+b)x+ab-c=0.

(2)有α(β+γ)+β(γ+α)+γ(α+β)=2(αβ+βγ+γα)=2b.由

[(αβ+βγ)+(βγ+γα)+(γα+αβ)]2=(αβ+βγ)2+(βγ+γα)2+(γα+αβ)2+2[(γα+αβ)(αβ+βγ)+(αβ+βγ)(βγ+γα)+(βγ+γα)(γα+αβ)]=2(αβ+βγ+γα)2-2αβγ(α+β+γ)+2[(αβ+γα)(βγ+αβ)+(βγ+αβ)(γα+βγ)+(γα+βγ)(αβ+γα)],

可得

α(β+γ)·β(γ+α)+β(γ+α)·γ(α+β)+γ(α+β)·α(β+γ)=b2+ac.

又

α(β+γ)·β(γ+α)·γ(α+β)=αβγ·(β+γ)(γ+α)(α+β)=abc-c2.

从而根为α(β+γ),β(γ+α),γ(α+β)的方程为x3-2bx2+(b2+ac)x+c2-abc=0.

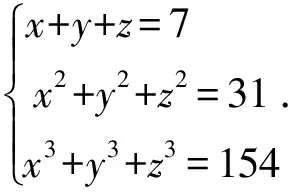
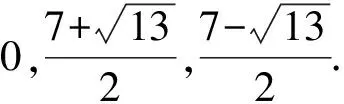
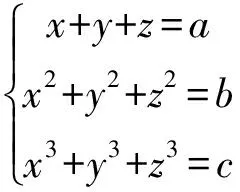
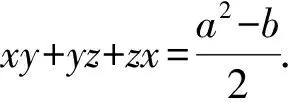
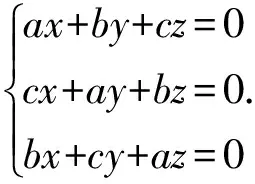
解考虑系数矩阵的行列式

由于a,b,c∈R且不全相等, 故(a-b)2+(b-c)2+(c-a)2>0.

当a+b+c≠0, 方程组的解为x=0,y=0,z=0.

当a+b+c=0, 系数矩阵秩为2, 此时(1,1,1)构成方程组的基础解系.

综合知原方程组的解为x=y=z=k(k∈C).

例33(1)说明x3-2x2-x+1=0的根均为实根.

(2)设x3-2x2-x+1=0的根a>b>c, 求a2b+b2c+c2a和ab2+bc2+ca2.

解(1)设f(x)=x3-2x2-x+1, 有f(-1)=-1,f(0)=1,f(1)=-1,f(3)=7, 由零点定理, 知f(x)在(-1,0),(0,1),(1,3)之间分别有一个实根, 故方程的根均为实根.

(2)记α=a2b+b2c+c2a,β=ab2+bc2+ca2.由(1)知c∈(-1,0),b∈(0,1),a∈(1,3), 易验证α>0.韦达定理说明了a+b+c=2,ab+bc+ca=-1,abc=-1, 此时

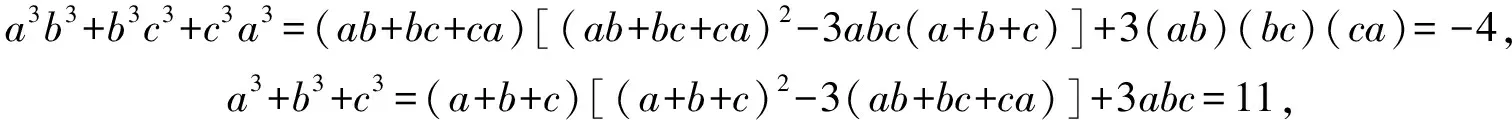
故αβ=-12, 解得α=4,β=-3.

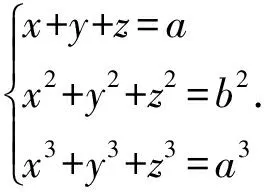
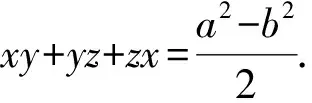
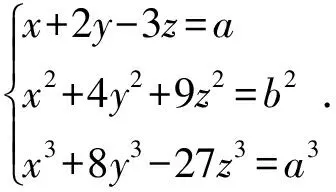
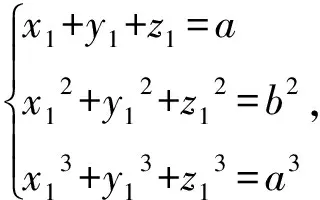
由例34可解得x1,y1,z1的值, 回代即得原方程组的解.

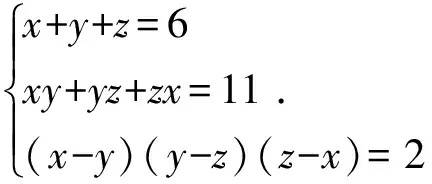
解令x1=x-y,x2=y-z,x3=z-x, 即x1x2x3=2且x1+x2+x3=0, 此时

故x1,x2,x3是方程t3-3t-2=0的3个根, 整理得(t+1)2(t-2)=0, 其解为-1,-1,2, 回代即得原方程组的解为1,2,3.

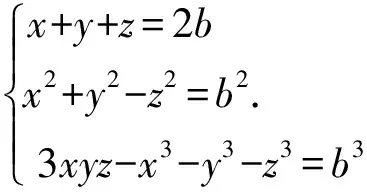
例38设a,b,c≥0,a+b+c=4,a2+b2+c2=6, 证明:a6+b6+c6≤a5+b5+c5+25.

例38的证明由(a+b+c)2=a2+b2+c2+2(ab+bc+ca), 得ab+bc+ca=5.

由a3+b3+c3-3abc=(a+b+c)[(a+b+c)2-3(ab+bc+ca)]=4, 得a3+b3+c3=3abc+4.此时由(a+b+c)3=(a3+b3+c3)+3(a+b)(b+c)(c+a), 得(a+b)(b+c)(c+a)=20-abc, 从而

a5+b5+c5=(a+b+c)5-5(a+b)(b+c)(c+a)(a2+b2+c2+ab+bc+ca)=55abc-76.

又a3b3+b3c3+c3a3=(ab+bc+ca)3-3abc(a+b)(b+c)(c+a)=3(abc)2-60abc+125, 故a6+b6+c6=(a3+b3+c3)2-2(a3b3+b3c3+c3a3)=3(abc)2+144abc-234.

从而要证的不等式变形为3(abc)2+144abc-234≤55abc-76+25, 即3(abc)2+89abc-190≤0, 分解得(abc-2)(3abc+95)≤0, 由于a,b,c≥0, 故只需证abc≤2.

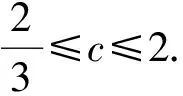
且F(1)=2,F(2)=2, 知F(c)=abc≤2, 得证.

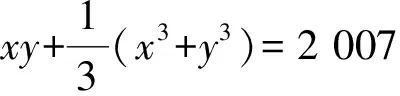
解有x3+y3-1+3xy=6 020, 故(x+y-1)[(x+y-1)2+3(x+y-xy)]=22·5·7·43.此时(x+y-1)3≡2(mod3),由Fermat小定理得x+y-1≡2(mod3).由于x,y都是整数,代回验证得x+y=21.此时xy=54, 从而x,y是方程t2-21t+54=0的根, 分解得(t-3)(t-18)=0, 故原方程的整数解为3,18.

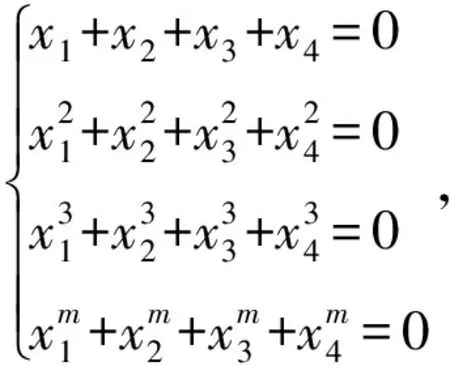
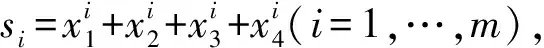
当m=4k,k∈Z时, 有

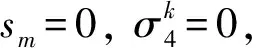
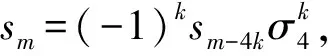
3 结束语

尽管作者手上还收集了不少练习题, 但是这组文章已经写得很冗长.运用文中的方法, 确实可以解决不少常见的问题, 但必须指出的是, 该方法的使用范围是有局限的.要是对本文例题里的条件或要证的结论做些改变, 本文中的方法就常常无能为力了.还有, 这个方法也常常不是最好的, 虽然用起来很顺手, 但在上面的一些问题上还远远没有深入到本质的现象.在接下来的文章里, 我们会对此展开必要的讨论.

作者感谢北京大学王杰教授及时的鼓励.