指向深度学习的教学策略

□沈敏芳

中华人民共和国教育部基础教育课程教材发展中心深度学习项目组提出，深度学习是指在教师的引领下，学生围绕具有挑战性的学习主题，全身心积极参与，以体验成功、获得发展的有意义的学习过程。在这个过程中，学生深度理解学习的内容，最终促进知识理解能力、问题解决能力、批判思维能力、创造性思维能力等的发展。

小学生的思维正处于从具体形象思维逐步向逻辑抽象思维发展的阶段，这为学生的数学深度学习准备了必要的条件。笔者认为，在教学实践层面上，可从“提问和讨论”“链接和建构”“反思和应用”这三个方面入手。

一、提问和讨论，让学习“深”一步

美国学者布鲁巴克指出，最精湛的教学艺术遵循的最高准则就是让学生自己提问题。《义务教育数学课程标准（2011 年版）》也指出：“学生学习应当是一个生动活泼的、主动的和富有个性的过程。教师要发挥主导作用，处理好讲授与学生自主学习的关系，引导学生独立思考、主动探索、合作交流，使学生理解和掌握基本的数学知识与技能、数学思想和方法，获得基本的数学活动经验。”

在数学课堂上，有了学生的主动提问，教学难点的突破就会变成学生自己的事情，不需要教师的反复讲解。学生自己提问、探究、交流、理解，这样的学习才有意义。

因此，在“有余数除法单元练习”一课中，笔者是这样安排教学的。

出示三道题：（1）9÷2=（ ）（2）29÷5=（ ）（3）45÷7=（ ），提问：“会做吗？”让学生用竖式计算。反馈之后，教师提出：“看看这三道题，你有什么发现？”学生思考后说都是有余数除法。教师接着说：“你有什么想问的？”等待片刻，学生提出了两个问题：（1）这几个数字分别叫什么？（2）它们之间有什么关系？

（教师用课件动态演示）

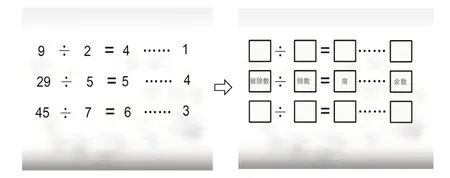
（三道题横式一点击马上变成3 个方框形式，接着3个横式合并成一个。□÷□=□……□）

师：有余数的除法，都可以表示成□÷□=□……□的形式，每个算式都有4 个数，谁知道它们各自的名称？（重复学生提出的第一个问题）

师：被除数、除数、商和余数之间有什么关系？（重复学生提出的第二个问题）

形成部分板书：

被除数÷除数=商……余数

余数＜除数

除数×商+余数=被除数

在这个环节中教师只说了“你有什么想问的”，学生就把自己的疑问提出来了。所提的两个问题看似简单，其实直指“有余数除法”的数学表达式的模型。教师根据学生的问题安排教学，重复学生提出的两个问题，使教学回到了学生这一学习主体身上。学生通过对比、交流，真正理解了有余数除法的模型。这也符合学生的思维习惯，相比传统的教学方式，他们更会在这样的过程中迸发学习的热情，绽放思维的个性。

二、链接和建构，使学习“广”一些

华东师范大学李士琦教授说：“学习一个数学概念、原理、法则，如果在心理上能组织起适当有效的认知结构，并使之成为个人内部知识网络的一部分，那么就说明他是理解了。”在知识由碎片化变为结构化的教学中，教师要搭桥引线，引导学生主动联结数学知识块、知识网，建构知识体系。这是学生数学学习的目标，“链接和建构”是实现目标的路径之一，也是“深度学习”的体现。

因此，教学人教版六年级下册“图形的运动复习”一课时，笔者对平移、旋转和轴对称三种运动方式进行简单的整理后，做了以下设计。

第一个层次：链接

师：通过刚才的复习，同学们对这三种运动方式有了新的认识，老师画了两幅图，请你们猜猜我是通过什么运动方式得到的？（两幅图一起出现）

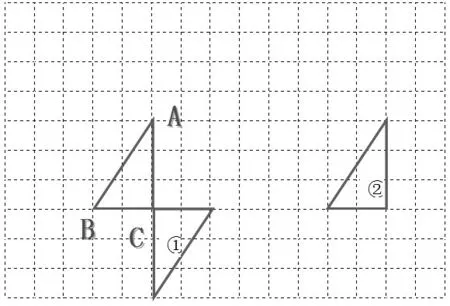
生：第1幅图是通过旋转得到的，第2幅图是通过平移得到的。

师：其实还有其他方法，大家再想一想。

生:我知道，第1 幅图是经过两次轴对称得到的。

师：对称轴在哪里？

生：对称轴是AC 所在的直线和BC 所在的直线。

师：你说对了，我的确是这样运动的。那第2幅图呢？

生：第2幅图也是通过两次轴对称得到的。

（课件配合学生的回答进行动态演示）

师小结：旋转和轴对称，平移和轴对称，不同的运动方式之间会有一定的联系，这里1次旋转相当于2次轴对称，1次平移相当于2次轴对称，有兴趣的同学可以课后再研究。

第二个层次：建构

师：用运动的眼光观察图形，会发现很多有趣的现象。不信，你看！这3 个图形是我们很熟悉的，用图形运动的眼光看有什么新的发现？

（出示一组平行线，一个等腰三角形，一个圆锥）

师：这是平行线，你觉得是哪种运动现象？

生：平移。

师：如果一条直线是另一条直线通过平移得到的，那么这两条直线互相平行。

师：看这个图形（等腰三角形），你想到了哪种运动方式？

生：轴对称。

师：这是轴对称运动吗？谁上来给大家演示？（剪一个三角形，对折）对称轴在哪里？

生：底边高所在的直线上。

师：对折后我们发现等腰三角形两边完全相等，所以不仅边相等，而且两个底角也相等。

师：（出示一个圆锥）你想到了哪种运动方式？师：直角三角形怎么旋转？

生：绕直角边旋转。

师：你还想到了哪些图形？你还能想到什么？

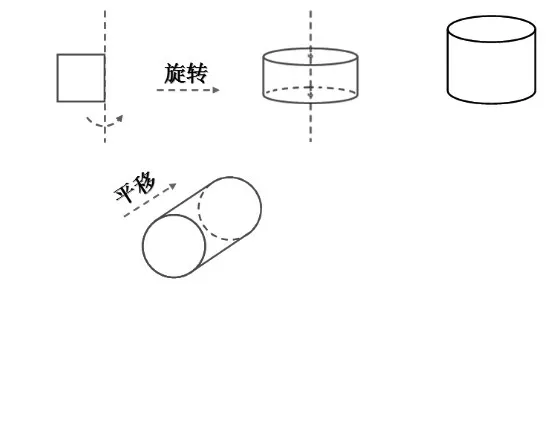
师：（出现一个圆柱）你想到了哪种运动方式？

生：旋转。

师：除了旋转，这个圆柱还可以通过哪种运动方式得到？

生：一个圆平移。

师：（结合学生回答动态演示图形运动的过程）是吗？还差一点！

师：（课件出示一个长方体）这个面可以看成是什么平移得到的？

生：一条线段平移得到的。

师：这条线段可以看成是什么平移得到的？

生：点。

师：（结合学生回答动态演示面、线再到点的过程）我们发现点运动成线，线运动成面。

师（小结）：这节课我们回顾了图形的运动，你有哪些收获？

生：我们知道了图形的平移、旋转和轴对称这三种运动方式之间有一定的联系。

生：用运动的眼光观察身边的物体会有很多新的发现。

教师在该教学环节中进行了两次知识的链接，分别是平移、旋转和轴对称以及点、线、面之间的链接，使学生对数学知识展开深度建构，对数学认知结构进行重组，促使学生的联结思维向纵深发展。

三、反思和应用，让学习“活”一点

有反思才有突破，有反思才有创新。让学生即时反思数学学习，能促进学生学习内化，实现深度学习。

首先，反思是深度学习不可或缺的一环。

学以“思”为贵。爱因斯坦说过：“学习知识要善于思考、思考、再思考。”的确，反思有利于学生由“被生长”走向“自生长”。

“毫米的认识”是人教版三年级上册“测量”单元的一个内容，学生罗××在学习之后，结合自己的认知写了下面这篇数学日记。

和“毫米”做朋友（片段）

……

原来我们要认识长度单位家族的新成员——“毫米”。毫米在哪里？我们从尺子上找，原来直尺上的一根根短竖隐藏着毫米，它可真调皮！每个1厘米之间都有，而且她们是个大家族，小伙伴很多，每隔1 厘米就会有10 个1 毫米，所以1 厘米=10 毫米，1分米=100毫米，而1米=1000毫米。毫米可真小，除了尺子上有毫米，哪里还有毫米呢？不久我们开始找了起来。沈老师告诉我们一张银行卡的厚度就是1毫米，我们拿出卡片用大拇指和食指轻轻地把它捏住，然后慢慢地把它抽走，大拇指和食指间细小的空隙就是1 毫米，这个空隙很小很小，两根手指差不多要碰到一起了。我们像一个个科学家一样，赶紧拿出直尺验证了一下，果然卡片的厚度藏了一个1毫米。我们又开始找了起来，我一眼看到了数学书，它的纸片很薄，我就跟同桌商量，几张纸的厚度是1 毫米呢？我们急急忙忙开始探索，一张、两张、三张……我和同桌两个人一个拿着书本的纸，一个拿着直尺，数着、量着，终于找到了——10张纸的厚度大约是1毫米，真的是太棒了！

……

爸爸跟我说，毫米虽小，但是它在我们生活中无处不在。通过测量我也感受到了毫米的存在。我想对毫米说：“毫米，你好！让我们交朋友吧！”

其次，应用实践是深度学习的外显展示。

灵活地将所学的知识应用于实践，是学生学习能力的表现。应用是将内化了的知识外显的过程，是培养学生数学素养的重要过程。

毕业班的学生在四年级时已会运用Word，在五年级信息课的学习中已经掌握了PPT制作，在此基础上笔者让所教班的学生制作微课，让学生把自己对知识的理解讲给同学听。具体从以下两方面推进。

1.合理分组。教师根据学情，把整个班级分成两类组，一类同质组，一类异质组，每个组两人。同质小组由水平相近的“中间层”学生组成，他们互无压力，敢于展示自我。异质小组由“异端水平”的两个学生组成，一个以小老师的形式就一个数学难题或数学知识点先给另一个同学进行讲解，等同学弄懂后，该生要负责后期的微课讲解。异质组与同质组组内分工虽有不同，但目标一致，就是弄懂知识点，并讲解微课。

2.细心指导。教师根据两类小组的特点，提出微课制作的目标，指导学生如何操作，让他们明确制作时该考虑些什么。

微课的最佳时长是5分钟左右，脚本设计应规范：视频有片头片尾；画面要生动，动静结合，图文并茂；难点的突破要有动态演示；静止的画面不应该超过10 秒；重点部分，字最好有闪一闪、跳一跳等的动态表现。教师要对设计脚本进行培训，同时要求信息教师对学生需要用到的PPT 和录屏软件等给予技术指导。

学生在整个实践中“真实践”“真思考”，将组内对知识的独特见解制作成短小精悍的微课视频，让“真学习”发生。学生制作的微课可能会有瑕疵，不完美，但显得珍贵。

综上所述，深度学习需要教师的引导和学生主体作用的发挥，只有师生的倾情投入，深度学习才能真正发生，学生的数学素养才能得以提升。