一种自适应的高维离群点识别方法
,,,
(江西中医药大学计算机学院,江西南昌330004)
高维数据中的离群点给数据分析工作带来了不便,比如在中药数据的药性有效成分分析、量效关系分析等数据分析过程中,由于离群点的存在使得数据分析结果有偏差或错误。数据分析工作中的部分数据高达成千上万维,随着数据维度的增长,当数据维度达到一定规模时,数据点的分布变得稀疏,就会出现“差距趋零”现象,将距离作为度量数据间差异的方式将会失效,这时传统的基于距离的离群点识别方法将无法直接有效地应用于高维数据中。常用的解决方法是先将高维数据映射到低维空间,再在低维空间应用相关算法进行离群点识别。
文献[1-4]提出使用PCA来提取数据样本的特征,但PCA是线性降维,只能提取数据间的线性关系,从而导致在处理高维数据时存在着统计特性的渐近性难以实现等问题;文献[5-10]采用了受限玻尔兹曼机(restricted Boltzmann machine,RBM)或高斯受限玻尔兹曼机(Gaussian restricted Boltzmann machine,GRBM)提取数据特征,其能够有效地、非线性地提取出高维数据的特征,但参数难以设定为较优值;文献[11]提出通过遗传算法优化RBM的网络权重等参数,但未对各层单元数进行具体优化。基于距离的离群点识别方法的算法思想简单有效,被广泛地研究和应用[12-17],其中文献[12-13]提出了针对不确定性数据和流数据的离群点识别方法;文献[15]提出了基于属性距离和的识别方法,但此类方法的识别准确率受用户指定的参数影响;文献[17]提出一种改进的、无需提供参数的基于距离和的识别方法。
基于此,本文提出一种自适应的高维离群点识别方法,该方法利用经遗传算法优化的GRBM对高维数据进行非线性特征提取,获得高维数据的较优低维表示,然后通过使用本文提出的自适应离群点识别方法对较优低维数据进行离群点识别。从理论上分析,该方法能有效地非线性提取出高维数据的特征,无需提供参数就可有效识别出高维数据中的离群点。
1 相关算法
1.1 GA-GRBM算法
受限玻尔兹曼机[18](RBM)是由可见层和隐藏层构成的基于能量的双层无向神经网络模型,层间相互连接,层内无连接。RBM默认其可见层单元是二值的,本文所用的是可见层单元为实值的GRBM,网络结构如图1所示。由于GRBM的输入单元是实值的,不用对输入数据二值化,因此不会造成数据信息的缺失,能更有效地提取出数据的特征。

图1 GRBM网络结构Fig.1 GRBM network architecture
GRBM的可见单元个数是输入数据的维度,隐藏单元的个数h、连接权重w和可见层偏置a,隐藏层偏置b的初始值可以通过文献[18]方法给出,但隐藏层单元数h设置是否合理将会影响到特征提取的结果,且不同的偏置值和隐藏层单元数组合有不同的特征提取效果。此外,随着数据维度增加,高斯受限玻尔兹曼机的参数也会增加,必然会导致算法的复杂度增加,因此本文应用遗传算法来寻找最优的a初始值和h参数组合,从而加速高斯受限玻尔兹曼机的优化参数速度,提出了遗传算法优化的GRBM方法(genetic algorithm-Gaussian restricted Boltzmann machine,GA-GRBM)。
GA-GRBM通过遗传算法找到最优的可见单元偏置初始值与隐藏单元数,相较于GRBM能够在更少的训练次数下更有效地提取数据特征。如图2所示,GA-GRBM的优化过程主要分为两个阶段。第一阶段是通过遗传算法寻找最优参数组合,首先将可见单元偏置a、隐藏层单元数h组合作为基因编码来随机初始化一个种群,将GRBM的重构误差作为适应度函数,之后根据适应度函数来选取、交叉、变异形成新的种群。以此种方式开始遗传迭代,直到达到指定最大遗传次数或适应函数值变化趋于稳定,获得最优的参数组合。在GA-GRBM的第二个阶段中,将最优的参数组合解码作为GA-GRBM模型的隐藏层单元个数h和可见单元偏置a的参数初始值,其他参数初始值按照文献[19]中的方式设置;然后采用对比散度方法来快速精调GRBM参数,获得一个稳定的GA-GRBM模型,最后利用此模型将高维数据非线性地映射到低维空间。

图2 GA-GRBM流程图Fig.2 GA-GRBM flow chart
值得注意的是,GA-GRBM是一种自编码和解码的非线性提取特征方法,能在尽量不损失原有特征信息的条件下,获得更低维的强解释的综合特征。比如高维数据样本o(o1,o2,…,on)经过非线性提取特征后变成低维数据样本p(p1,p2,…,pm),样本p是高维样本o的低维表示,其中oi≠pj;i∈n,j∈m;m 属性距离和的离群点识别方法认为离群点是指与数据集中其他所有数据对象的距离之和最大的前n个数据对象,该方法思想简单有效,但识别准确率却深受参数n的影响。为此,在属性距离和的离群点识别方法的基础上,提出了一种自适应的离群点识别算法(adaptive outlier recognition method,AORM),该方法无需人为设置参数就可以自适应地输出离群点。 AORM算法运用了盒图[19]的思想,不需要提供任何参数就可以有效识别出离群点,解决了基于距离的离群点识别方法对参数敏感的问题。AORM首先计算每个数据对象与数据集中其他数据对象的距离,得到距离矩阵M;然后依次对矩阵的每一行求和,得到数据对象到其他数据对象的距离之和的集合S(s1,s2,…,si),并将该集合升序排序;最后根据盒图的原理自动输出离群点。AORM方法的具体步骤如下。 输入:数据集D。 输出:离群点。 1)计算数据集合D中各个数据对象之间的属性距离dij,得到距离矩阵M; 3)对步骤2)得到的距离之和的集合S(s1,s2,…,si)升序排序; 4)计算S的max值Smax,再将si与Smax比较,si值大于Smax的数据对象都被识别为离群点; 5)输出离群点。 其中Smax=Q3+1.5IQR,IQR=Q3-Q1,Q3和Q1是集合S的上四分位数和下四分位数。 随着数据维度的增长,当数据维度达到一定规模时,数据点的分布变得稀疏,若使用常用的距离测度(比如欧氏距离),数据点之间的距离将趋于相等,这就是“差距趋零”现象;这时传统的基于距离的离群点识别方法将无法直接有效地应用于高维数据集。基于此,本文将GA-GRBM算法和AORM算法组合优化,提出了一种自适应的高维离群点识别方法(adaptive high-dimensional outlier recognition method, AHORM)。 AHORM模型的结构如图3所示,AHORM的思想是利用GA-GRBM算法将高维数据映射到低维空间,之后在低维空间中使用基于距离的自适应的离群点识别方法输出离群点。模型的具体构建过程如下: 1)遗传算法优化GRBM。 (a)随机初始化种群,种群中的每个个体都是可见层偏置a和隐藏层单元数h组成的基因编码片段; (b)将GRBM的重构误差作为适应度函数,对种群进行选择、交叉和变异,得到新种群; (c)循环步骤(b),直到达到收敛条件停止遗传,得到最优参数组合。 2)GA-GRBM提取数据特征。 (a)将最优基因片段解码作为GA-GRBM可见层偏置初始值和隐藏层单元数,再利用对比散度方法训练模型、精调参数,构建一个稳定GA-GRBM特征提取模块; (b)利用GA-GRBM将高维数据非线性地映射到低维数据空间,得到高维数据的最优低维表示。 3)AORM自适应识别离群点。 (a)计算低维数据各自之间的距离得到距离矩阵,对矩阵的每一行求和并升序排列; (b)根据盒图原理找出属性距离和异常的数据对象,输出离群点。 图3 AHORM模型结构Fig.3 AHORM model structure AHORM模型的优势在于可以有效地应用于高维数据,通过将高维数据映射到低维空间,避免“差距趋零”现象的发生;这时基于距离的离群点识别方法不再失效,可以通过AHORM模型中的AORM算法模块自适应地输出数据中离群点。 本节对GA-GRBM算法、AORM算法和AHORM算法分别做了对比验证实验,所有的实验环境均为Windows10(64位)操作系统,Intel Core i5-3470 CPU@3.2GHz,8GiB内存,Pycharm Python3.5编程平台。 首先将GA-GRBM与传统的GRBM做了对比验证实验。实验数据采用了UCI数据集(http://archive.ics.uci.edu/ml)中的Communities and Crime数据集,该数据经处理后包含了1 000个数据样本,每个样本各有112个属性。传统GRBM的可见层单元数为样本属性个数112,各层偏置和权重初始值、隐藏层单元数根据文献[18]中的方法设定,权重w的初始值由正态分布(0,0.01)生成,各层偏置初始值为零,隐藏层单元数根据数据信息估算给出。GA-GRBM的可见层偏置初始值和隐藏层单元数由遗传算法确定,其他参数设定同传统GRBM一样。遗传算法的种群个数100,父代个数和子代个数均为50,当遗传代数达到100时停止遗传。 如图4,实验记录了在不同训练次数(epoch)的情况下两种GRBM的重构误差(reconstruction error)变化情况,其中重构误差是在同一个epoch值下,各实验5次取的平均值。从图4可以看出,随着epoch值的增加,两种GRBM的重构误差呈现出先减小后震荡增加的趋势,这是训练从欠拟合到刚好拟合再到过拟合的过程。 GRBM的重构误差变化较剧烈,在epoch值为80的时候剧烈下降,然后epoch值为500时降到最小值0.384。相较与GRBM,GA-GRBM的曲线变化比较平缓,在epoch值为150的时候达到最小值0.365,之后随着epoch值的增加而增加。 图4 重构误差随epoch值变化图Fig.4 Reconstruction error versus epoch value 以上分析说明了两点: 1)GA-GRBM和GRBM分别在epoch为150、500时,重构误差达到了最小值,这表示GA-GRBM相对GRBM能够用更少的训练次数快速学习到数据的特征; 2)GA-GRBM具有比GRBM更小的重构误差,表明GA-GRBM比GRBM能够更好地拟合原数据。 为了验证AORM的有效性,将AORM算法与属性距离和算法做对比实验。实验数据取自UCI数据库的BTSC数据集(blood transfusion service center data set)、CMC数据集(contraceptive method choice data set)、AD数据集(audit data set)、BCW数据集(breast cancer Wisconsin data set)和WI数据集(wine data set),属性维度分别为4、9、13、18、30维,每个数据集都含有5%的离群数据,离群数据的每一维由均匀分布随机生成[20]。属性距离和算法的参数n的取值为数据集样本个数的5%取整,AORM无需设置参数。用运行时间(T)、精确率和召回率的调和均值(F1值)作为实验效果评价指标,对比实验评价指标结果见表1。 表1 GA-GRBM对比实验结果 从运行时间T来看:属性距离和算法与AORM算法的运行时间相差无几,两者都能较快速地识别出低维数据中的离群点。从调和均值F1值来看,在对实验数据有所了解的情况下,AORM的F1值要略高于属性距离和方法。倘若在对数据的分布不够了解的情况下,通过人为给定离群点个数的方式相对于AORM的自适应识别方式会有更差的识别率。 综上所述,属性距离和算法与AORM的对比实验结果证明了AORM方法是能够有效地、自适应地识别出低维数据中的离群点。 表2 AHORM对比实验结果 为了验证AHORM方法的有效性,本文选取了UCI机器学习数据集的4组数据做了对比验证实验。并用江西中医药大学现代中药制剂教育部重点实验室的两组中药数据验证AHORM方法对高维中药数据离群点识别的有效性。 来自UCI机器学习数据集的4组数据分别是:PD数据集(Parkinson’s disease)、SCADI数据集、Musk数据集、DG数据集(Dota2Games result),其维度分别为756、206、166、116维。来自江西中医药大学现代中药制剂教育部重点实验室的两组中药数据分别是:CHD寒热药数据,数据特征有249个;中药光谱数据NIR中药数据集,属性是波长,属性的取值为中药成分在该波长下的吸收率,有1 557个属性。采用不同维度的数据集进行试验,可更好地评估算法性能。对于每个数据集,分别将其中的70%用作训练集,30%用作测试集。训练集中混有20%的离群数据,测试集中混有5%的离群数据,离群数据的每一维由均匀分布随机生成[20]。 对比实验将基于PCA及属性距离和的离群点检测算法和PCA-SVM[21]两个方法作为参照算法。按照通常的做法,本文将PCA的贡献比率阈值都定义为98%,SVM中的核函数采用径向基核函数 RBF;为模拟现实中参数n的取值情况,将基于PCA及属性距离和算法的参数n设置为数据样本容量的5%~10%的随机数取整。AHORM中的遗传最大次数为100,种群个数为100,父代个数和子代个数均为50;权重w的初始值由正态分布(0,0.01)生成,隐藏层偏置初始值为零,可见层单元数为样本数据维度,学习率为0.1,当epoch超过300次停止训练。用P值、R值、F1值作为实验效果的评价指标,实验结果见表2。图7、图8分别是3种算法在UCI数据上和在中药数据上的对比实验结果图。 从表2和图7、图8可以看出: 1)在UCI数据上,AHORM的P值相较于PCA-SVM平均提高了8.3个百分点;调和均值F1值平均提高了4.6个百分点;在两组中药数据的对比实验中,AHORM的F1值比PCA-SVM算法平均高了5.2个百分点。 2)相对于PCA及属性距离和算法,从精确率P值来看,AHORM在两种数据集上的P值都高于PCA及属性距离和的P值,最高相差0.230,最低相差0.016。差值波动大是n的取值随机造成的,说明了n的取值好坏对实验结果影响很大。从调和均值F1值来看,AHORM在5组数据的F1值比PCA及属性距离和算法平均提高了5.9个百分点。 以上分析说明,本文提出的AHORM算法可以有效地应用于高维数据的离群点识别当中。 图7 UCI数据实验结果Fig.7 UCI dataexperimental results 图8 中药数据实验结果Fig.8 Traditional Chinese medicine data experimental results 针对传统的基于距离的离群点识别方法难以直接有效地应用于高维数据且识别效果受参数影响的问题,本文提出了一种自适应的高维离群点识别方法(AHORM),充分利用了经遗传算法优化后的高斯受限玻尔兹曼机的强大非线性特征提取能力,以及基于距离的自适应离群点识别方法(AORM)简单有效的优势。在UCI高维数据和中药高维数据上的对比实验中,AHORM算法相对于两种对比算法,各项评价指标均有所提升,其中F1值平均提高了5.6个百分点,证明了AHORM方法具有更好的识别效果,是一种能有效地应用于高维数据的离群点识别方法。1.2 自适应的离群点识别算法

2 自适应的高维离群点识别方法
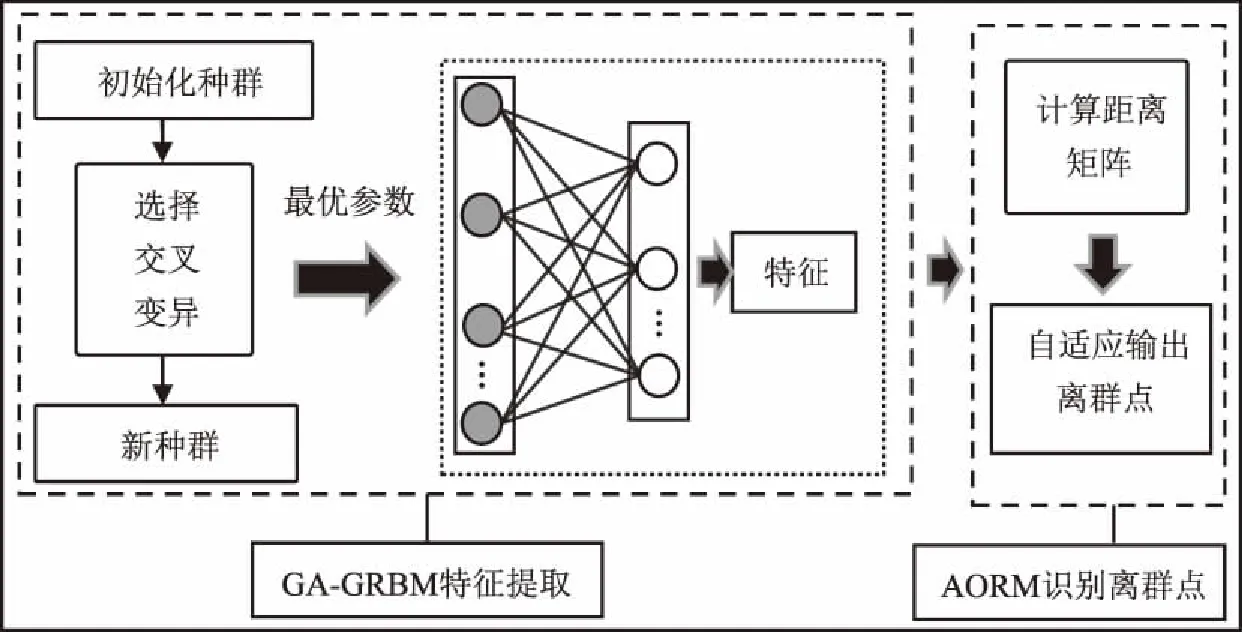
3 实验与分析





4 结束语

