一种面向不平衡分类的改进多决策树算法
,,,
(1. 山东师范大学信息科学与工程学院,山东济南250358;2. 山东省分布式计算机软件新技术重点实验室,山东济南250358;3. 山东警察学院公共基础部,山东济南250014)
在不平衡分类问题[1-3]中,样本数量较少的称作少数类或正类,样本数量较多的称作多数类或负类,许多实际数据集中两类样本之间的比例往往差距悬殊,并且大多数不平衡数据集中存在类重叠现象及噪声样本,这对于研究分类问题无疑带来更多困难和挑战。一些传统分类器在处理不平衡分类问题时,为了提高整体分类准确率,会忽视少数类样本对整体的影响,无法将它们准确分离出来;而少数类样本中往往包含更重要的信息,因此分离少数类样本成为一个棘手的问题。目前解决不平衡分类问题主要的方法有改变数据分布、集成学习等。改变数据分布最常见的方式为过采样和欠采样。过采样[4-7]是指增加少数类样本来保持数据平衡,例如Chawla等[4]提出的SMOTE。之后研究者将很多方法与SMOTE结合提升了算法性能,如KM-SMOTE[6]、IDP-SMOTE[7]等算法。欠采样[8-10]通过删除多数类样本来保持数据平衡,如随机欠采样方法。Lin等[10]提出的基于聚类的欠采样CBU(clustering-based undersampling),虽然有效地提高了分类效果,但仍然可能忽略部分重要信息。集成学习[11-20]通过训练多个个体分类器并进行结合,能够得到比单一分类器更好的泛化性能。经典的集成学习方法如 RUSBoost[14]、UnderBagging[15]、 EasyEnsemble[16]等,都在一定程度上提升了分类器的性能。很多情况下将欠采样与集成学习结合使用效果更好。Kang等[17]提出集成欠采样方法EUS(ensemble under-sampling),从多数类中多次抽取与少数类相同数目的样本形成多个平衡样本集,在一定程度上克服了欠采样的信息丢失问题。Lu等[18]提出一种自适应决策边界的集成方法(adaptive ensemble undersampling-boost),引入了一种自适应的阈值确定方法。Nejatian等[20]采用集成欠采样方法,训练决策树作为基分类器,虽然效果有所提升,但对于决策树的训练面临着根节点的属性选择问题,如果盲目随机地选择分裂属性,会对分类结果产生一定的影响。
针对上述问题,本文提出一种基于欠采样与属性选择的多决策树方法UAMDT。首先对多数类样本进行Tomek link欠采样[21-22],然后通过集成欠采样方法对多数类样本进行随机有放回采样,采样的数量与少数类样本数量相同,将采样后的多数类与少数类样本结合成多个平衡子集进行集成学习。本文选择决策树作为基分类器,为了进一步精确分类结果,采用一种混合属性度量[23]作为属性选择标准,混合属性包含信息增益与基尼指数,基于不同的根节点信息构建多决策树。
1 基于欠采样与属性选择的多决策树方法UAMDT
为了降低类重叠现象对分类的影响,保持原始数据的分布,提升总体分类精度,本文提出一种改进的多决策树方法UAMDT,主要包括3个阶段:①利用Tomek link欠采样去除多数类样本中的噪声;②通过集成欠采样合成多个子训练集;③训练嵌入属性选择标准的决策树进行集成分类。
1.1 Tomek link欠采样技术
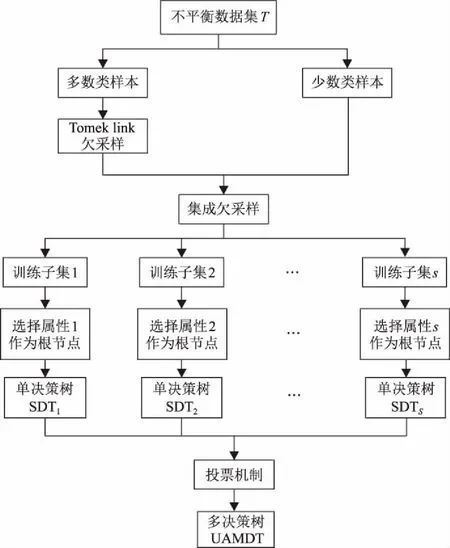
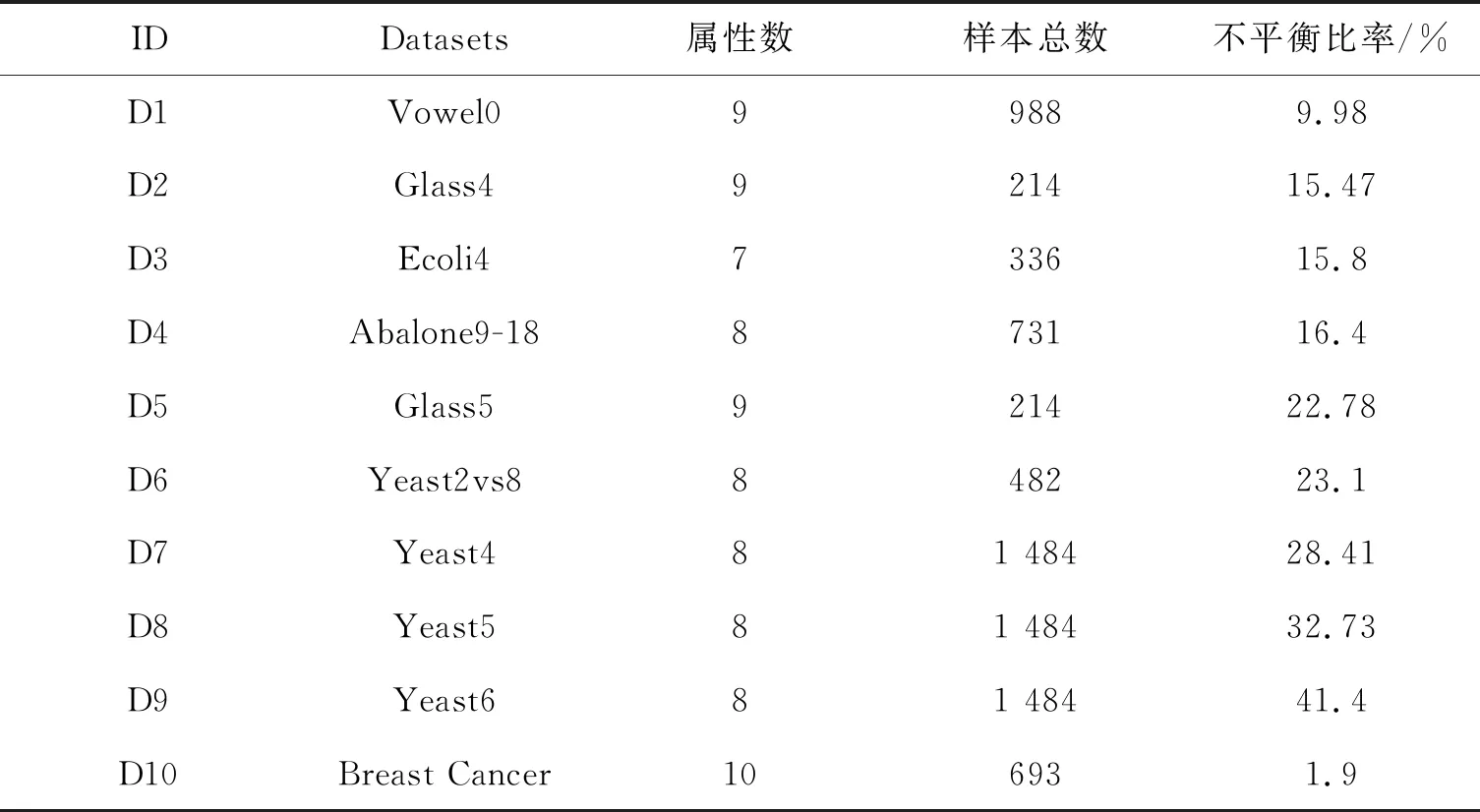
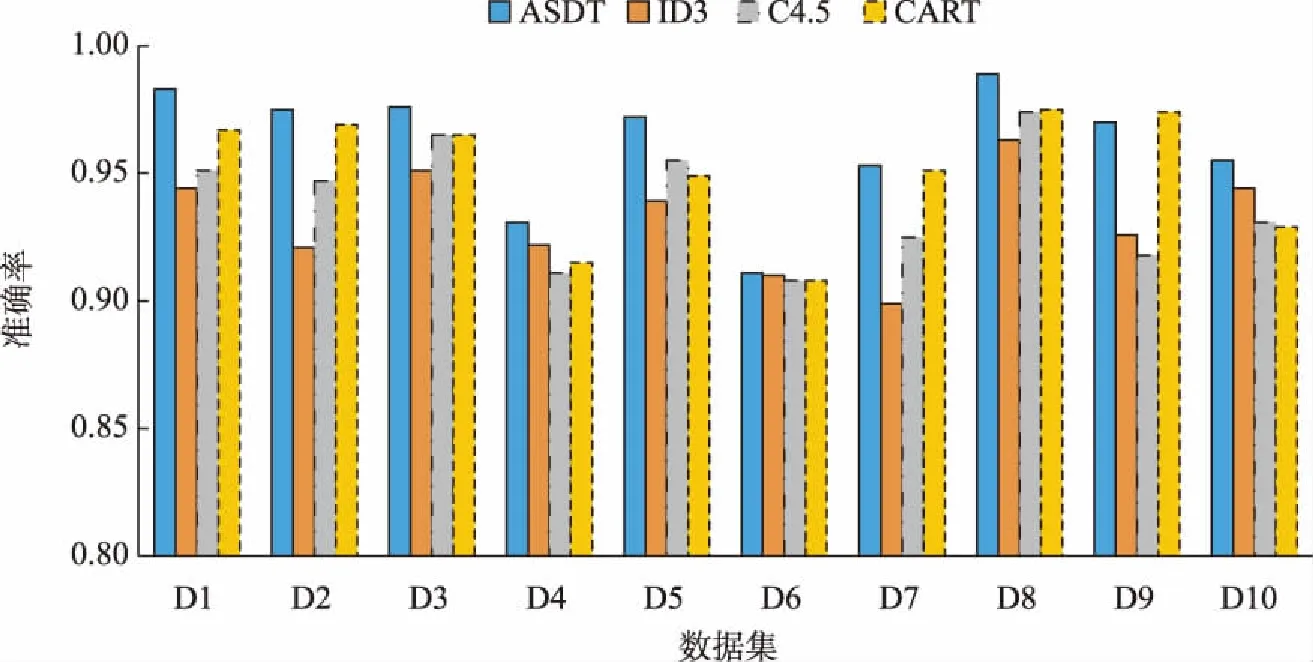
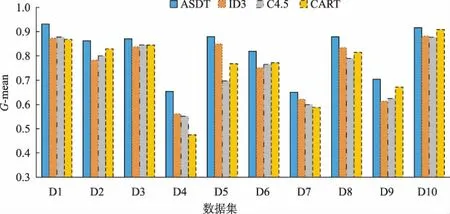
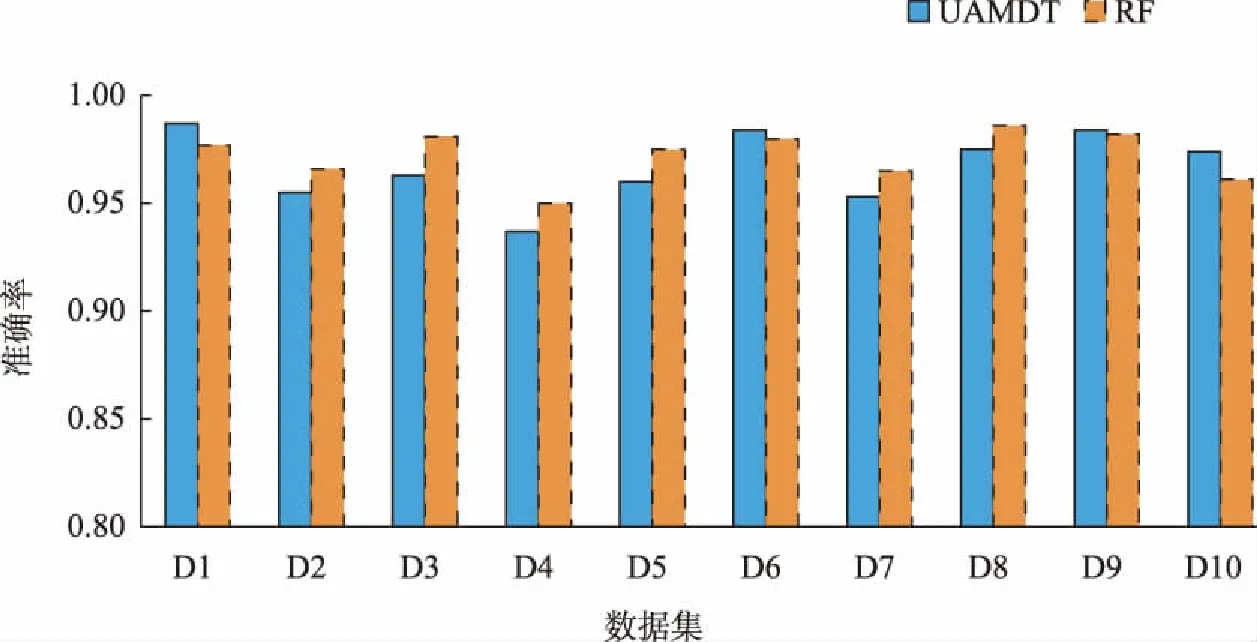
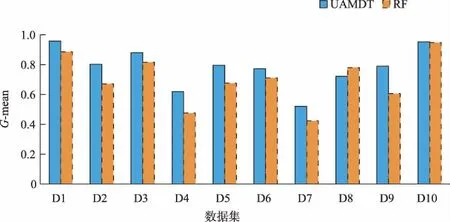
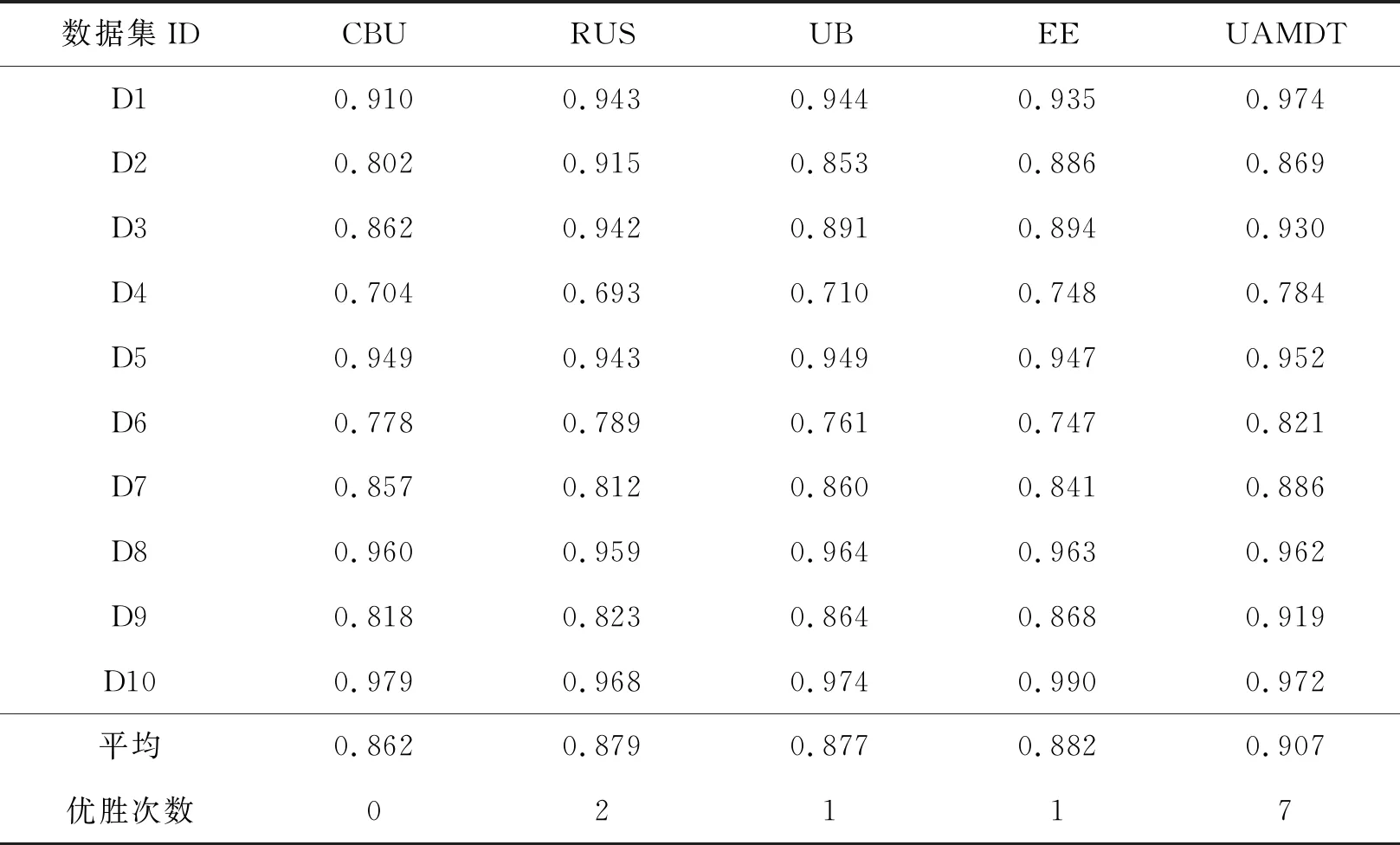
Tomek[14]在1976年对CNN进行了改进,提出了一个新的框架,在数据空间中不破坏潜在信息的情况下对边界多数类样本进行欠采样,检测和删除多数类中的噪声数据。根据定义,如果两个样本属于不同类别且距离很近,则可将它们连接成一个Tomek link对,一旦两个样本构成Tomek link对,就意味着要么其中一个样本是噪声,要么两个样本都处于边界上。其基本思想是:给定一对样本(Si,Sj),Si属于多数类,而Sj属于少数类,两点之间距离记为d(Si,Sj),若不存在任意样本Sk,使得d(Si,Sk) 为了更有效地利用两类样本中潜在有用的信息,保证每个集成分类器的多样性,在进行数据处理时,首先对进行Tomek link欠采样之后的多数类样本Smaj进行s次随机有放回采样,每次采样的样本数目Mi与少数类样本数目Smin相同,即|Mi|=|Smin|。然后将采样后的多数类样本与少数类样本组合成新的子训练集Ti,此时每个子训练集都是平衡的,即不平衡比率rIR=1。具体过程如算法1。 算法1: Input:多数类样本集Smaj,少数类样本集Smin,采样次数s。 Output:子训练集集合{Ti|1≤i≤s}。 Procedure: 1.i=1; 2.从Smaj中随机有放回采样Mi个样本,|Mi|=|Smin|; 3.新训练子集Ti=Mi∪Smin; 4.i=i+1; 5.重复2~4步直到i=s; End。 对整个训练集进行Tomek link欠采样及集成欠采样技术之后,形成的s个子训练集上分别构建单决策树分类器。决策树是一种基于训练样本的属性对其进行分类的树形结构,从根节点到分支节点,递归地选择最优的划分属性,将整个数据集划分成纯度更高、不确定性更小的子集,最终将分类结果赋予叶子节点。如果不适当地选择根节点属性,选择的效果将沿着分支扩散到叶子,会导致最后分类错误率增加,因此选择哪个分裂属性作为根节点至关重要。已经有一些属性选择准则,如信息增益(ID3决策树)、信息增益比(C4.5决策树)以及基尼指数(CART分类树)等,都是用来度量样本集纯度的方式。 信息增益代表基于某个属性划分数据集前后不确定性的减少程度,因此信息增益越大,集合的纯度越高。它偏向于多值属性,独立地度量每个训练集的纯度,所以对于类概率向量分量中的排列不敏感。基尼指数表示在样本集合中一个随机选中的样本被分错的概率,因此基尼指数越小,样本被分错的概率越小,集合的纯度就越高。假设某训练子集包含m个属性值A1,A2,…,Am,类标签由k表示,因为二分类问题中只有两类样本,因此k=1,2。将两种度量线性结合,定义混合属性度量h(α)如下: h(α)=αG(Ai)-(1-α)I(Ai)。 (1) 其中:G(Ai)表示基于分裂属性Ai划分数据集的基尼指数;I(Ai)表示基于分裂属性Ai划分数据集前后的信息增益;α是加权系数,表示每个度量的相对贡献度。基尼指数G(Ai)定义如下: (2) (3) 其中:N表示数据集T的样本总数;Nk表示属于第k类的样本数量;Pk表示选中的样本属于第k类的概率。 信息增益I(Ai)可表示为划分数据集前后熵的差值,定义如下: I(Ai)=E-E′, (4) (5) (6) 其中:E表示划分数据集之前的熵值;E′表示划分数据集之后的熵值;n表示基于属性Ai划分数据集之后的子集数;Nj表示第j个子集的样本数。 利用混合属性度量可以将信息增益与基尼指数的优点相结合,同时弥补两者的缺陷。由于混合属性度量h(α)由信息增益与基尼指数线性结合,信息增益越大,基尼指数越小,h(α)越小,集合的纯度越高,因此应该选择具有最小h(α)值的属性Ai作为根节点的分裂属性。 因此,在每个训练子集上构建单决策树时,将训练子集中包含的所有属性按h(α)值大小进行排列,选择具有最小h(α)值的属性作为该决策树的根节点的分裂属性。 将多个单决策树进行集成预测的多决策树算法,预计分类结果比单决策树更准确。因此,本文采用投票机制构建多决策树,对于每一个样本,集成所有单决策树的分类投票结果,将投票次数最多的类别指定为最终的输出。本文提出的基于欠采样与属性选择的多决策树方法UAMDT如算法2,流程图见图1。 算法2: Input:训练集T,权重系数α,采样次数s。 Output:集成分类器UAMDT。 Procedure: 1.将多数类样本进行Tomek link欠采样,记为Smaj,少数类样本记为Smin; 2.i=1; 3.从Smaj中随机有放回采样Mi个样本,|Mi|=|Smin|,采样次数为s,产生子训练集集合{Ti|1≤i≤s},Ti=Mi∪Smin; 4.将子训练集Ti中的属性值按属性选择标准h(α)=αG(Ai)-(1-α)I(Ai)进行排序,寻找h(α)最小的属性值; 5.将h(α)最小的属性值作为根节点的分裂属性,训练单决策树SDT1; 6.i=i+1; 7.重复步骤3~6直到i=s; 8.采用投票机制,集成单决策树SDT1,SDT2,…,SDTs的分类投票结果,构建多决策树UAMDT; End。 图1 UAMDT算法流程Fig.1 UAMDT flowchart 为评估本文算法对不平衡分类的有效性和可靠性,选择KEEL数据库中的9个不平衡数据集D1~D9以及来自于UCI的Breast cancer数据集D10进行实验,选取的数据集的样本总数在214至1 484之间,不平衡比率在1.9到41.4之间。具体数据集如表1所示。 表1 数据集 对于不平衡数据分类,最常见的评估标准有G-mean、准确率Accuracy、AUC值等。三者的定义需要用到表2的混淆矩阵。 表2 混淆矩阵 通常用G-mean值用来评测一个算法的综合性能,定义为: (7) (8) (9) 其中:RTP是真正类率,表示正类样本分类正确的概率;RTN是真负类率,表示负类样本分类正确的概率。如果分类器偏向某一类,那么G-mean值会很小,所以G-mean值越大,分类器的性能越好。 准确率ηAccuracy表示分类预测正确的样本占总样本的比例,定义为: (10) 为了全面验证本文提出的UAMDT算法对于不平衡数据分类的有效性,在10个数据集上设计了3个对比实验。在实验中将集成欠采样的抽样次数s设置为20,权重系数α设置为0.6。实验采用五折交叉验证,实验1与实验2使用G-mean值与准确率作为分类器评价指标,实验3使用AUC作为评估标准。 实验1:为了验证属性选择标准的适用性,将ASDT与ID3、C4.5、CART单决策树进行对比实验。ASDT算法是在原始数据集上对多数类样本进行Tomek link欠采样之后,选择h(α)最小的属性作为根节点的分裂属性训练单一决策树。 图2和图3分别给出了ASDT与ID3、C4.5、CART算法的准确率和G-mean值比较,实验结果表明,ASDT的平均准确率优于其他3种方法,其次分别是CART、C4.5和ID3。而图3显示ASDT的G-mean值明显高于ID3、C4.5和CART,原因是ASDT相对于其他3种算法而言,具有更精细的属性选择标准,ASDT结合了信息增益与基尼指数两种准则,充分结合了两种度量的优势,而其他3种算法使用的是单一属性选择标准。ID3算法只使用了信息增益作为分裂标准,但信息增益偏向取值较多的属性;C4.5算法作为改进,以信息增益比作为属性选择标准,在信息增益的基础上增加一个惩罚参数;CART决策树以基尼指数作为分裂标准,但CART是二叉树,只能根据某个属性将数据分配到两个集合。实验证明了混合属性选择标准的适用性和有效性,并且当选择对分类结果更有影响的属性时分类效果更好。 图2 ASDT与ID3、C4.5、CART的准确率比较Fig.2 Comparison of accuracy between ASDT and ID3, C4.5, CART 图3 ASDT与ID3、C4.5、CART的G-mean值比较Fig.3 Comparison of G-mean between ASDT and ID3, C4.5, CART 实验2:为了验证本文算法UAMDT对于不平衡分类的可行性,将随机森林RF与UAMDT算法进行对比实验。随机森林是一种经典的多决策树算法,本质是集成学习的Bagging方法,训练多个单决策树进行集成。 图4和图5分别给出了UAMDT和RF的准确率和G-mean值比较,实验结果表明,两种方法的准确率没有较大差异,相差最大值为0.018。而除了数据集D8之外,UAMDT的G-mean值都高于随机森林RF。随机森林RF是在Bagging的基础上改进的算法,Bagging算法是对数据集进行随机放回抽取多次,形成多个训练集,而这些训练集可能是不平衡的,并且它们的不平衡比率也可能不相同。而本文提出的UAMDT是经集成欠采样之后,在多个平衡训练集上训练决策树,且在每棵决策树的根节点加入了对应训练集中使分类效果最好的分裂属性,因此UAMDT的性能优于随机森林RF。 图4 UAMDT与RF的准确率比较Fig.4 Comparison of accuracy between UAMDT and RF 图5 UAMDT与RF的G-mean值比较Fig.5 Comparison of G-mean between UAMDT and RF 实验3:将UAMDT算法与已经提出的一些经典算法进行比较,包括CBU(clustering-based undersampling)、RUS(RUSBoost)、UB(UnderBagging)、EE(EasyEnsemble)算法。表3给出了5种算法在10个数据集上的AUC值及平均值,实验表明除了数据集D2、D3、D8及D10之外,UAMDT都获得了最高的AUC,且平均值也达到最高值0.907,其次分别是EE、RUS、UB和CBU算法。综合看来,UAMDT优胜次数多达7次,明显提高了分类性能。UAMDT算法相较于其他4种方法来说,采用Tomek link欠采样降低了类重叠对数据集的影响,减小了不平衡比率IR,对于之后的分类起到了一定的作用,包括采用集成欠采样技术,这些数据处理措施使得UAMDT对于区分少数类样本具有更强的适应性。 表3 CBU、RUS、UB、EE、UAMDT等5种算法的AUC值比较 针对不平衡分类问题,为了更有效地利用数据信息,保持数据原始分布,本文利用集成学习的思想,提出一种基于欠采样与属性选择的多决策树方法UAMDT,对多数类样本进行Tomek link欠采样与集成欠采样,在增大两类样本之间距离的同时,保留数据信息,保证了训练子集的多样性和差异性,使得训练的各基分类器可以处理不同的数据。混合属性度量结合了信息增益与基尼指数两种度量的优点,在每个训练子集中寻找使分类效果最好的属性,作为每棵决策树根节点的分裂属性。最后利用投票机制将单决策树的预测结果汇合,构建最终的多决策树。本文在来自KEEL以及UCI数据库中的10个不平衡数据集上进行了3组对比实验,以准确率、G-mean值以及AUC作为评估分类性能的指标,实验结果表明本文算法对整体分类性能有了明显的提升,说明了本文算法在不平衡分类领域是有效和可行的。实验亦证明本文算法可用于一些具体应用领域,如在医疗方面预测和诊断疾病等,从而发现异常,使患者及时得到医治。 本文在选取分裂属性时,并未考虑属性对各样本的影响程度,并且本文只选取了小型数据集进行实验,在一些数据集上效果一般,对于大型数据集不确定是否同样适用尚未可知,因此,在之后的研究工作中,需要对算法进行细节的改进,并针对效果较差的数据集以及大型数据集进行进一步的考察和研究。1.2 集成欠采样技术
1.3 属性选择标准
1.4 UAMDT算法设计
2 实验设计
2.1 数据集
2.2 评估标准

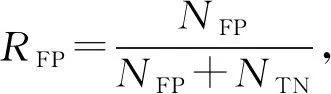
2.3 实验结果与分析
3 结束语

