基于LSTM神经网络的锂离子电池荷电状态估算

明彤彤，王凯，田冬冬，徐松，田浩含

(青岛大学，山东 青岛 266000)

据世界卫生组织统计，每年有650万人因空气污染而过早死亡。2015年在氮氧化合物污染统计中，交通运输业占其中50%，共排放氮氧化合物5.3×107t[1-3]。挪威等欧洲国家正考虑在2025年前禁止汽油和柴油动力汽车上路。锂离子电池由于其较高的能量密度被广泛应用在电动汽车领域，同时在无人驾驶汽车、无人机和智能电网领域的应用也在不断增长[4]。

电池荷电状态(state of charge，SOC)的精确估计是电力设备稳定运行的关键，对于监测车辆的剩余里程和电池均衡系统至关重要[5-7]。但电动汽车在行驶过程中反复变速给精确估计SOC带来了挑战。SOC是指电池的剩余电量除以其出厂容量，一般来说SOC是温度、充放电电流倍率的非线性函数[8-10]。测量电池SOC的基本方法有开路电压法、安时积分法和基于电池内阻的预测方法。安时积分法通过测量电池电流再对电流进行积分来实现SOC预测，对电流精度要求较高[11-13]；开路电压法的缺点是预测前需要电池长时间静置，不适合在线测量[14-16]；基于电池内阻的预测法受电池种类、数量和一致性的影响，很少在电动汽车上使用[17-20]。以上3种方法局限性较大，已被其他更为复杂的算法取代，如自适应观测器、滑模观测器和卡尔曼滤波，但这些算法一般计算复杂，通常需要额外的参数和不同的模型以适应不同情况下的SOC估计。

20世纪90年代，数据和硬件限制了机器学习的发展。2012年之后机器学习取得了巨大的进步[21]，硬件的发展、数据的收集、算法的改进推动了机器学习的发展。从1990年到2010年，非定制中央处理器(central processing unit，CPU)的速度提高了5 000倍。2016年，Google在其年度I/O大会上展示了张量处理器(tensor processing units，TPU)项目，其开发目的完全是为了运行深度神经网络[22-24]。互联网的高速发展，使得收集和分发超大型数据集变得可行。除了硬件和数据之外，算法的改进实现了更好的梯度传播，使得深度学习发展迅速。

本文提出了一种基于长短期记忆(long short-term memory，LSTM)循环神经网络的锂离子电池SOC估计方法。使用TR9600可编程直流电子负载对所选锂离子电池进行多工况放电实验，高精度地采集测试数据。使用Keras深度学习框架，将TensorFlow作为后端引擎，搭建前馈(back propagation，BP)神经网络、门控循环单元(gated recurrent unit，GRU)和LSTM神经网络进行性能对比。在模型的训练过程中，将数据分为训练集、验证集和测试集，在训练集上训练模型，在验证集上评估模型，并调整网络最佳配置参数，在测试集上进行性能测试。选用带动量的随机梯度下降(stochastic gradient descent，SGD)作为优化器，以防止模型陷入局部最小点，增加模型的收敛速度。在LSTM循环神经网络基础上加入Dropout正则化方法，以增强模型的泛化能力。

1 LSTM循环神经网络模型

百度研发中心开发了一种基于循环神经网络(recurrent neural network，RNN)的深度学习语音识别系统——Deep Speech 2，其识别的准确度超过人类正常水平。BP神经网络和卷积神经网络(convolutional neural networks，CNN)的共同特点是没有记忆前面输出的状态变量，单独处理每个输入，在输入和上次输出之间没有任何联系。对于BP神经网络和CNN，想要处理数据点或时间序列，需要向网络同时展示整个序列，在现实的机器学习过程中往往难以实现。

1.1 循环神经网络

BP神经网络和CNN假设所有输入数据都是独立的，这种假设对于序列化数据不成立。时间序列数据呈现出对前面数据的依赖，这被称为长期趋势。循环神经网络(recurrent neural network，RNN)用隐藏状态或者记忆引入这种依赖，以保存当前的关键信息。任一时刻的隐藏状态是前一时间步中隐藏状态和当前时间步中输入值的函数，即

ht=φ(ht-1,xt).

(1)

式中：ht为时间步t的隐藏状态(下标“t”代表时间步t，下同)；xt为时间步t的输入。RNN采用这种方式对任意长度的序列化数据进行编码和合并信息。

RNN单元如图1所示。图1中：yt为时间步t的输出；u、v、w分别为权重矩阵U、V、W的元素，分别对应输入、输出和隐藏状态。输出yt的一部分反馈给神经单元，以在稍后的时间步t+1上使用。

图1 RNN单元Fig.1 RNN Unit

与传统的神经网络工作原理类似，训练RNN涉及误差的反向传播，存在梯度消失和梯度爆炸问题。梯度消失的影响为相距较远的时间步上的梯度对学习过程没有任何用处，因此RNN不能进行大范围依赖学习。有几种方法可以最小化梯度消失问题，如W权重向量的适当初始化、使用ReLU替代tanh层、使用非监督方法预训练网络等，最流行的方案是使用GRU或LSTM网络架构，这些架构被设计成处理梯度消失问题。

1.2 LSTM循环神经网络

LSTM循环神经网络是RNN的一个变体，适用于学习长期依赖。图1演示RNN如何在tanh层使用前一时间步的状态和当前输入来实现递归。LSTM也以类似的方式实现了递归，但并不是1个单独的tanh层，而是以特别方式交互的4个层。图2展示了LSTM循环神经网络单元结构，其中，i为输入门，o为输出门，f为遗忘门，g为内部隐藏状态，ct为时间步t的单元状态，方框内为神经网络层。

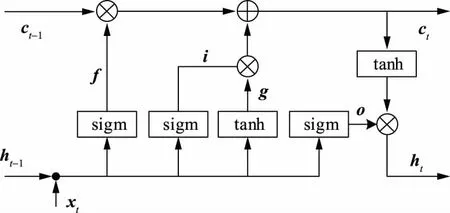
图2 LSTM 循环神经网络单元Fig.2 LSTM Unit

图2上部的线是单元状态，i、f、o和g门是LSTM解决梯度消失问题的关键。在训练过程中，LSTM为这些门进行参数学习。下列等式显示了它是如何通过前一时间步的隐藏状态ht-1来计算时间步t的隐藏状态ht。

ft=σ(Wf·[ht-1,xt]+bf)，

(2)

it=σ(Wi·[ht-1,xt]+bi)，

(3)

gt= tanh(Wg·[ht-1,xt]+bg)，

(4)

ot=σ(Wo·[ht-1,xt]+bo)，

(5)

ct= (ct-1ft)⨁(gtit)，

(6)

ht= tanh(ct)ot.

(7)

式中：W为各层神经网络权重矩阵；b为各层网络的偏置矩阵；下标“i、f、o、g”分别对应i、f、o门和内部隐藏状态；σ为sigmod函数。

遗忘门定义前一状态ht-1的多少部分可以通过，而输出门定义当前状态的多少部分揭示给下一层，内部隐藏状态g基于当前输入xt和前一状态ht-1计算。给定i、f、o和g，根据时间步t-1上的状态ct-1，乘以遗忘门，就能计算时间步t的单元状态ct；乘以输入门i，就能计算出状态g。最后，时间步t的隐藏状态ht通过将记忆ct和输出门相乘来计算。

本实验输入向量由电压、电流组成。搭建BP神经网络、GRU和LSTM神经网络进行性能对比。利用dSPACE可以高精度测量电流的特性，用安时积分法进行SOC的精确计算。在LSTM神经网络基础上添加Dropout正则化，以增强模型的泛化能力。

2 实验测试

本文所选取的实验对象是博沃尼克公司生产的通用型锂离子动力电池，其额定容量为1.5 Ah，额定电压为3.7 V，充电截止电压为4.2 V，充电截止电流为0.02 C(44 mA)，放电截止电压为2.75 V。

18650动力锂离子电池的测试平台由直流电子负载、dSPACE MicroLabBox实验箱以及计算机组成，测试平台如图3所示。

图3 锂离子电池测试平台Fig.3 Testplatform of Li-ion battery

所用电子负载为埃用仪器有限公司的TR9600可编程直流电子负载。数据由dSPACE MicroLabBox RTI1202进行高精度数据采集。使用Keras深度学习框架，将TensorFlow作为后端引擎，搭建BP神经网络、GRU和LSTM神经网络。图4是实验具体流程。

图4 实验流程Fig.4 Experiment flow chart

2.1 特征工程提取

特征工程是指将数据输入模型之前，利用关于数据和机器学习算法的知识对数据进行硬编码变换，以改善模型的效果。大多数情况下机器学习模型无法从完全任意的数据中进行学习，呈现给模型的数据应该便于模型进行学习。特征工程的本质是用更简单的方式表述问题，从而使解决问题的方式变得简单，良好的特征工程可以用更少的资源解决问题。如果样本数量有限，特征信息就会变得至关重要。开路电压法用电池电压作为SOC预测的参数，安时积分法利用放电电流进行SOC预测。考虑在实际工况以及SOC与电池电压、放电电流的映射关系，本文选用电池电压、放电电流作为特征参数。所用参数在电池使用过程中易于测量，可行性较高。

2.2 特征数据采集

本实验采用恒流放电和动态放电2种放电模式，实现不同工况下的数据采集。在恒流放电模式下，不论输入电压如何变化，电子负载始终消耗恒定的电流；在动态放电模式中，设定低电位电流和高电位电流，电子负载会连续在低位电流和高位电流之间来回切换电流值；在放电过程中，每隔1 s提取电池电压、电流和SOC。实验数据划分见表1。

表1 实验数据划分Tab.1 Experimental data division

将实验数据分为训练集、验证集、测试集。在训练集上训练模型，在验证集上评估模型，并调整网络最佳配置参数，在测试集上进行测试。验证集存在的原因在于调节模型配置，比如选择层数或每层大小，调节过程需要使用模型在验证数据上的性能作为反馈信号，调节的过程本质上就是一种学习。但基于模型在验证集上的性能调节模型配置，会导致模型在验证集上过拟合。每次基于模型在验证集上的性能来调节模型超参数，会有一些关于验证集的信息泄露到模型中，所以需要加入测试集，来验证神经网络在新数据上的表现。

2.3 数据预处理

在训练LSTM神经网络之前，需要将数据处理为神经网络可以处理的格式，数据是数值型的，但输入向量数据中的每个量纲单位(电压、电流)位于不同的取值范围，需要对量纲进行标准化处理，让不同输入维度在相似的范围内取较小的值。一般来说，将取值较大的数据(如电压数据)输入网络是不安全的，这样会导致较大的梯度更新，进而导致网络无法收敛，为了让网络的学习变得容易，输入数据应有以下特征：①取值较小，大部分值应在[0,1]范围内；②具有同质性，所有特征的取值都应在大致相同的范围内。

归一化操作是深度学习模型训练之前要进行一项重要的操作。本文采用的归一化方法为Min-Max标准化，也称离差标准化，是对原始数据的线性变化，将结果映射到[0,1]之间。其公式为

(8)

式中：Xnorm为归一化后的值；X为归一化前数据的值，Xmax、Xmin为其最大值和最小值。该方法把数据压缩到[0,1]之间，是原始数据的等比压缩。

2.4 损失函数的选择

确定了网络架构，还需要选择损失函数，损失函数是衡量预测精度的具体表现。本实验采用平均绝对误差(mean absolute error，MAE)作为损失函数，用其检测预测值和真实值之间的偏差。具体公式为

(9)

式中：M为本实验的平均绝对误差；fi为预测值；yi为真实值；n为将要进行预测的数据量。改进神经网络，意味着通过改变权重减小损失函数值。

2.5 优化器选择

优化器是使用损失值进行梯度更新的具体方式，本文选用带动量的SGD作为优化器，动量解决了SGD的2个问题：收敛速度和局部极小点。在损失函数某个参数值附近有一个局部极小点，在这个点附近，无论向哪个方向调整，都会导致损失值增大。如果使用小学习率的SGD进行优化，优化过程很可能会陷入局部极小点，导致无法找到全局最小点。

使用动量方法可以避免这样的问题，这一方法将优化过程想象成从损失函数曲线上滚下来的小球。如果小球的动量足够大，那么它不会卡在局部最小点里，最终会达到全局最小点。动量方法的实现过程是每一步都移动小球，不仅要考虑当前的斜率值，还要考虑当前的速度。这在实践中指的是更新权重不仅要考虑当前的梯度值，还要考虑上一次的参数更新。

2.6 模型超参数设置

为提高模型性能，应对模型超参数进行调整。使用的模型应该具有足够大的容量，以防欠拟合，即模型应避免记忆资源不足，在容量过大和容量不足之间找到一个折中。

为测试模型超参数对性能的影响，在LSTM神经网络基础上改变网络层数和每层神经元个数。图5显示了改变模型超参数后在测试集上的MAE，其中每层大小代表神经元个数。从图5可以看出：当模型为3或4层时， MAE数值较低，性能较为可靠；当模型层数超过4层时，MAE大幅提升，并且随着每层神经元个数的增加，模型性能下降明显。

图5 模型超参数对性能的影响Fig.5 Effect ofparameters on model performance

3 实验结果分析

3.1 3种神经网络性能对比

完成网络架构调整后，在相同的实验数据上训练模型。图6和图7分别是BP神经网络、GRU和LSTM神经网络在恒流放电和动态放电情况下的绝对误差(absolute error，AE)。表2和表3展示3个模型在测试集上的最大绝对误差和MAE。3个模型均使用MAE作为损失函数，评估数据和评估指标完全相同，可以直接比较3种方法的结果。实验所用计算机CPU型号为i7-6700。在训练周期为80次的情况下，BP神经网络、GRU、LSTM神经网络训练耗时分别为189 s、598 s、895 s。

可以看出，在恒流放电模式下， LSTM神经网络和GRU性能较为理想，与BP神经网络相比预测更为准确。在动态放电情况下，LSTM神经网络的预测精度较BP神经网络、GRU提升明显。从2种工况下的实验结果可以看出，LSTM神经网络性能较为理想。

3.2 使用循环Dropout降低过拟合

过拟合存在于所有机器学习的问题中，降低过拟合，提高网络的泛化能力(即模型在前所未见的数据上的性能)，是机器学习中至关重要的一步。为了防止模型从训练数据中学到错误或无关紧要的模式，最优解决办法是获取更多的训练数据，模型的训练数据越多，泛化能力越强。如果无法获取更多数据，次优解决方法是调节模型允许存储的信息量，或对模型允许存储的信息加以约束，这种降低过拟合的方法称为正则化。

图6 BP、GRU、LSTM恒流放电预测绝对误差Fig.6 Absolute errors of constant current discharge prediction of BP、GRU and LSTM

图7 BP、GRU、LSTM动态放电预测绝对误差Fig.7 Absolute errors of dynamic discharge prediction of BP、GRU and LSTM

表2 恒流放电情况下的表现Tab.2 Performance under constant current discharge

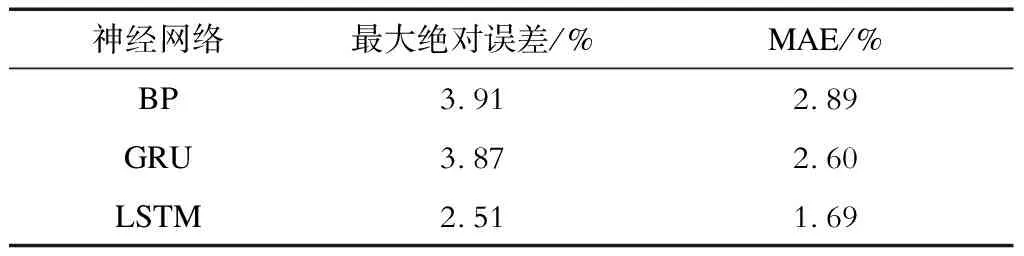
表3 动态放电情况下的表现Tab.3 Performance under dynamic discharge

Dropout是神经网络有效正则化的方法之一，它由多伦多大学的Geoffrey Hinton 和他的学生开发。对某一层使用Dropout，就是在训练过程中随机将该层的一些输出特征舍弃(设置为0)。假设在训练过程中，某一层对给定输入样本应该是向量(4.2，0.5，24)，使用Dropout后，这个向量会有几个随机元素变成0，比如变为(4.2，0，24)。Dropout比率是被设为0的特征所占的比例，通常在0.2～0.5范围内。

本实验对LSTM循环神经网络加入Dropout正则化方法，实验结果如图8所示。在实验过程中发现将Dropout比率设为0.3时，训练效果最为理想。添加Dropout正则化后最大绝对误差为2.0%，MAE为1.05%，低于实际应用要求的5%，满足实际应用要求，性能较为可靠。

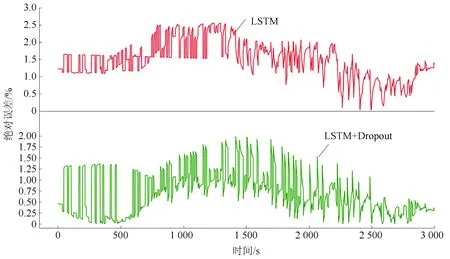
图8 动态放电加入Dropout后模型在测试集上的性能Fig.8 Performance of the model on the test setafter dynamic discharge adding Dropout

4 结论

本文针对物理建模预测锂离子电池SOC方法存在的不足，提出采用基于LSTM的锂离子电池SOC估计方法。基于本文实验与讨论结果可以得出以下结论：

a)本文提出的锂电池SOC预测方法不涉及锂电池的工作原理，克服了不同工况下建立不同模型的缺点，具有较好的适用性和推广性；

b)在训练过程中，采用带动量的SGD作为优化器，防止模型陷入局部最小点，增强了模型的收敛速度；

c)加入Dropout正则化方法，降低了网络的过拟合现象，增强了模型的泛化能力，进一步提高了神经网络的预测性能；

d)与BP神经网络、GRU相比，本文所采用方法具有更好的预测精度，为准确估计不同工况下锂离子电池SOC问题提供了研究基础，在电动汽车领域具有很好的应用价值。