基于分式函数约束的稀疏子空间聚类方法
王雨思,路德杨,李海洋
1.西安工程大学 理学院,西安710048
2.广州大学 人事处,广州510006
3.广州大学 数学与信息科学学院,广州510006
1 引言
聚类分析作为数据挖掘和模式识别等领域的重要工具,一直得到广泛的应用。但是,随着信息时代的来临,高维数据变得越来越普遍。在处理高维数据时,传统聚类方法,如k-means[1]等,表现出两方面不足。一方面,这些方法通常采用距离作为相似性度量来进行聚类,而高维空间中的数据较低维空间中的数据分布要稀疏,且数据间距离处处相等是非常普遍的现象;另一方面,高维数据集中存在大量的无关属性,这些无关属性使得在数据集中存在簇的可能性几乎为零。研究表明,高维数据往往存在于低维流形结构中,而不是均匀的分布在任意空间,且它们的本质维数比其真实的维数要低得多[2]。如含有数百万帧的影像资料,刚性运动物体的轨迹特征[3],不同光照条件下的人脸图像[4]等都位于低维联合子空间中。因此,子空间聚类应运而生[5]。
子空间聚类作为高维数据聚类的一种新方法成为当前的研究热点。常用的子空间聚类主要分为以下4类:迭代方法、代数方法、统计方法和基于谱聚类的方法[6]。目前,基于谱聚类的子空间聚类方法在众多算法中是比较成功的。它首先通过搜索数据点之间的关系,利用相似性构建亲和矩阵(Affinity Matrix);然后基于图论的原理利用谱聚类方法对亲和矩阵进行聚类;最后得到聚类结果[7]。基于谱聚类的子空间聚类方法的关键是如何更好的构建数据点之间的关系,使得亲和矩阵能够更有效的表示数据间的相似性,这对聚类效果的影响至关重要。当前构建亲和矩阵的方法主要有ε-邻近法、k 邻近法和全连接法等,其中全连接法选择使用高斯核函数RBF 或Sigmoid 核函数来刻画数据点之间的关系,是目前应用中最普遍的方法。
针对如何有效的建立亲和矩阵的问题,基于高维数据的自表征特性,即每个依存于子空间并上的数据点都能被数据集中其他数据点的组合所表示,Elhamifar 和Vidal 在文献[8]中提出了稀疏子空间聚类算法(Sparse Subspace Clustering,SSC)[9-10]。文献[11]提出了基于低秩表示的子空间聚类方法(Low Rank Representation,LRR)[12-13],与其他较好的子空间聚类算法相较,基于稀疏和低秩表示的方法不需要先验条件可以直接处理噪声和异常点。文献[14]结合稀疏性与低秩性提出了多子空间表示(Multi-Space Representation,MSR)模型。文献[15]同时对系数矩阵进行稀疏和低秩正则项约束,提出了LRSSC(Low-Rank Sparse Subspace Clustering)模型。文献[16]结合稀疏表示的局部性和流行学习思想,提出了局部子空间聚类(Local Subspace Clustering,LSC)方法。虽然上述一系列的模型和算法很大程度的提高了子空间聚类的性能,但遗憾的是,上述这些方法皆采用矩阵的核范数或向量的1-范数对亲和矩阵和稀疏随机噪声进行约束。然而核范数或1-范数约束得到的最优解往往不够稀疏,不能准确反应高维空间中数据分布的稀疏性以及稀疏随机噪声的位置和大小,对聚类结果产生了不利影响。
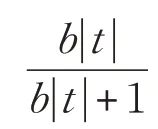
鉴于分式函数良好的稀疏性,本文主要把分式函数应用于子空间聚类,研究内容如下:(1)在稀疏子空间聚类模型中以分式函数作为目标函数代替0-范数,并证明了该模型所求的稀疏系数矩阵具有块对角结构,能够更好地揭示出数据的子空间结构。(2)本文针对含噪声情况,将含噪数据分解为干净数据、高斯噪声和异常点噪声,并对异常点噪声仍旧采用分式函数约束作为正则项,提高模型的鲁棒性。(3)利用交替方向迭代方法(alternating direction iteration method)[18]对模型进行求解,得到稀疏系数矩阵,进而求出相似性矩阵,最后将相似性矩阵应用于经典的谱聚类方法进行聚类。本文结构图如图1所示。

图1 文章结构图
2 相关知识
2.1 子空间聚类
定义1(子空间聚类Subspace Clustering)给定位于n 个联合线性子空间并上的N 个无噪声数据点,子空间相互独立,子空间Si对应的维数为di,定义数据矩阵X:
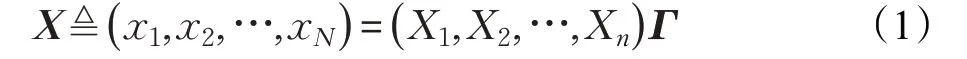
其中Xi∈RD×Ni是一个秩为di(N >di)的矩阵,表示第i个子空间数据点组成的矩阵;Γ 为未知置换矩阵。子空间聚类的目的是求解子空间的个数n 以及它们对应的维数di,同时将数据点xi分割到原本对应的子空间中,理想情况下每一类对应一个子空间。
为了解决子空间聚类问题,基于数据的自表征特性,Elhamifar 和Vidal 提出稀疏子空间聚类(SSC)算法。该算法运用理想情况下,数据点的稀疏表示中的非零元素对应于来自相同子空间的数据点这一特性,通过一个稀疏优化框架,获得不同子空间的数据划分,再根据这一信息使用谱聚类框架获取聚类结果。SSC 的基本思想是将矩阵X 表示成字典矩阵D 下的线性组合,即X=DC,同时希望线性组合的系数矩阵C 是最稀疏的,SSC的基本模型如下:
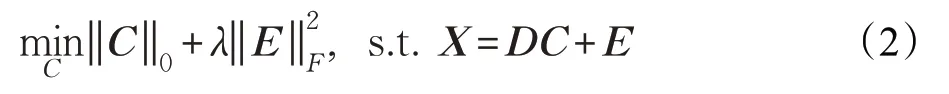
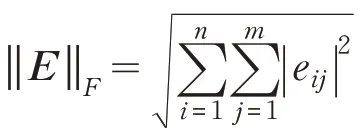
由于0-范数的最小化求解是一个NP-hard 问题,故一定条件下,上述0-范数优化问题等价于下式所示的凸1-范数优化问题:

2.2 分式函数及其主要特性
本文考虑利用分式函数逼近0-范数来提高模型的稀疏性。以下给出分式函数的定义及其主要性质。
定义2[17](分式函数)对于任意的t ∈ℝ,定义分式函数pb(t)为:
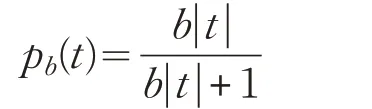
其中参数b ∈( 0,+ ∞)。
在分式函数中:当t=0 时,pb(0)=0;当t0 且参数b →+∞时,pb(t)→1,可见随着参数b 的增大它能够逼近0-范数。图2 给出在不同参数下的分式函数图像。
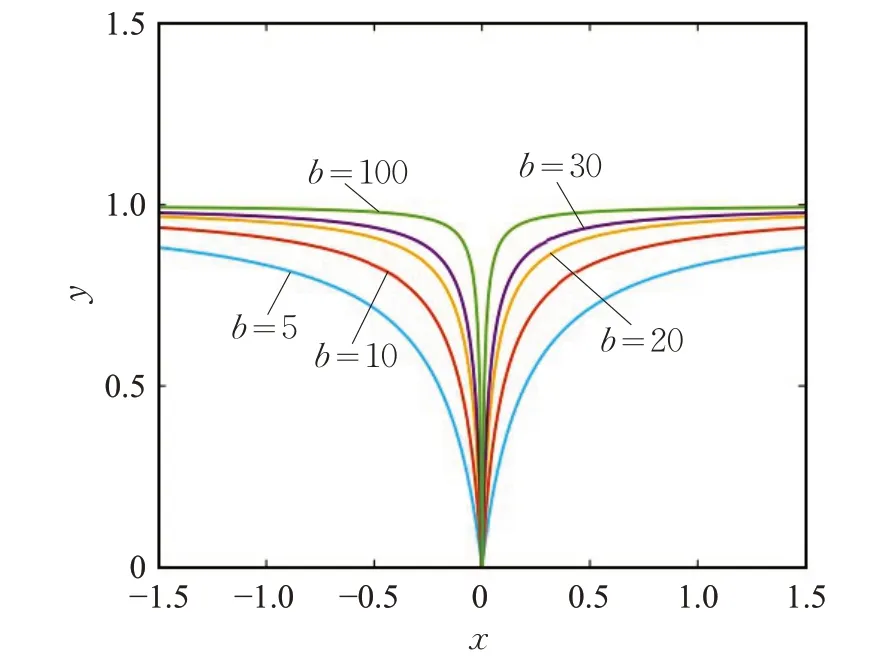
图2 不同参数下的分式函数图像
因此分式函数pb(| t|)可以近似逼近0-范数,即

2.3 分式迭代阈值算法
在求解0-范数优化问题中,迭代阈值算法作为一种成功的方法被广泛应用在压缩感知中。其中迭代硬阈值算法(Iterative Hard Thresholding,IHT)[19]主要是将0-范数优化问题转化为求解无约束0-范数优化,迭代硬阈值算法的迭代格式为:
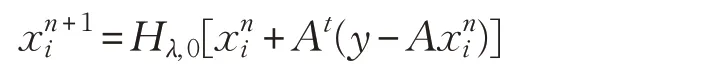
其中:
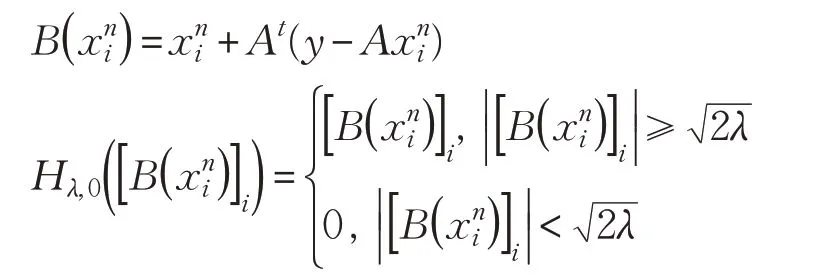
迭代软阈值算法(Iterative Soft Thresholding)[20]主要求解无约束的1-范数优化问题,其迭代格式如下:
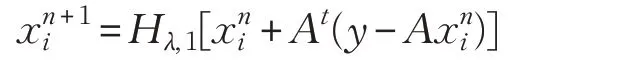
其中:

分式迭代阈值算法在文献[17]被提出并应用于压缩感知中,表现出良好的性能,其迭代格式通过定理1给出。
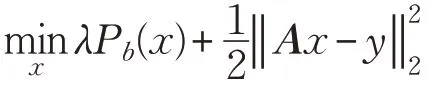

其中:
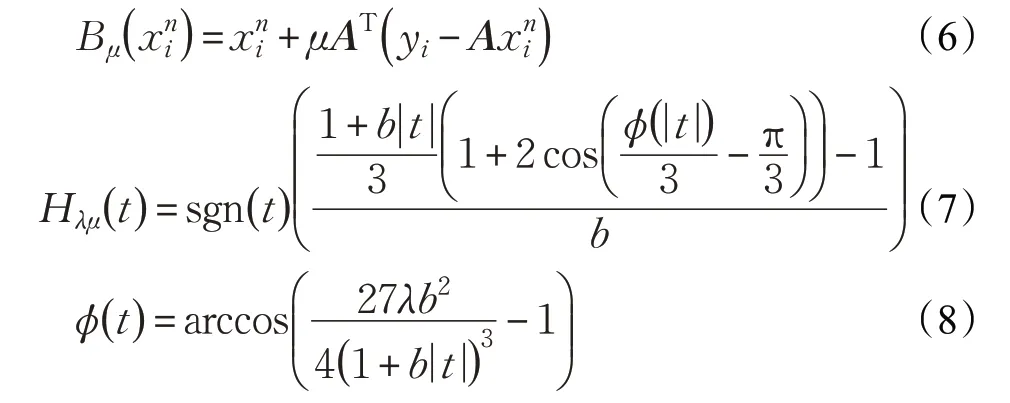
故X*的第i 列为:

其中参数t 满足:
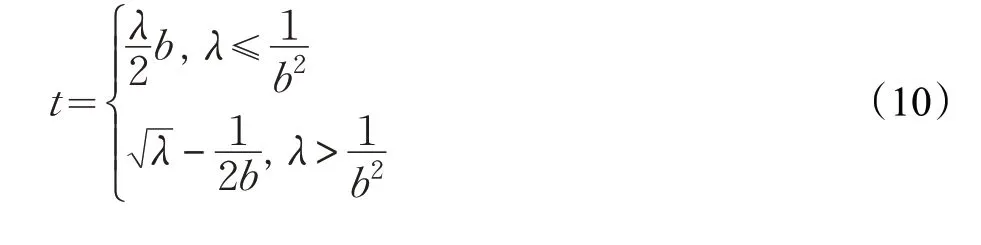
3 基于分式函数约束的稀疏子空间聚类模型
本章提出基于分式函数约束的稀疏子空间聚类模型(Fraction function Penalty Sparse Subspace Clustering,FPSSC),相较于经典的凸1-范数约束的稀疏子空间聚类模型,FPSSC能获得比凸1-范数约束稀疏性更好的系数矩阵。
3.1 构建模型
分式函数可以逼近0-范数且较凸1-范数逼近获得的系数矩阵更加稀疏,同时较0-范数易于求解。因此本文用分式函数替代不连续的0-范数,将0-范数约束问题:
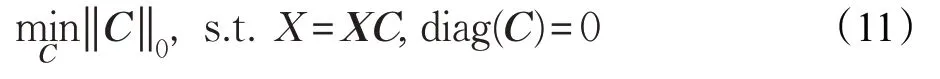
转化为如下基于分式函数的约束问题:
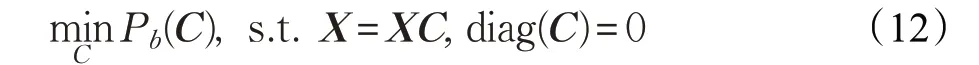
通常情况下,SSC目标函数的目的是保证子空间中数据点的表示系数矩阵具有良好的有利于子空间聚类的结构,即具有块对角结构[21]。文献[22]在假设数据无噪声干扰、子空间相互独立的情况下,提出强制块对角(Enhance Block Diagonal,EBD)条件。该强制块对角条件能够保证子空间表示系数矩阵,即所求模型的最优解具有块对角结构。下面证明本文构建的模型(12)在求解过程中获取的系数矩阵C 具有块对角结构。
强制块对角条件(Enforced Block Diagonal conditions,EBD):函数f 是一个定义在上的矩阵集。对于任意其中A和D是方阵,B 和C 是任意维数的兼容矩阵。令则有强制块对角条件:
(1)对任意置换矩阵P,ZP ∈Ω,有f( Z )=f( ZP)。
(2)f( Z )≥f( ZD),当且仅当B=C=0(或Z=ZD)时等式成立。
(3)f( ZD)=f( A)+f( D)。
引理1[22]假设数据样本充分且子空间相互独立,若函数f 满足EBD条件(1)、(2)、(3),则模型:

的最优解Z*一定是块对角结构:
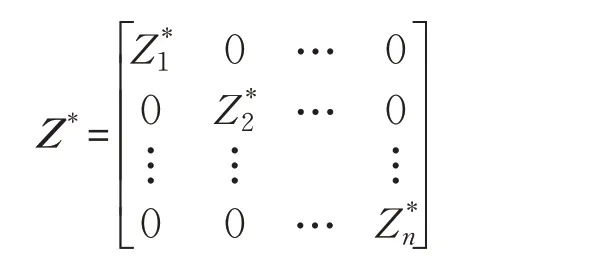
定理2假设数据样本充分,且子空间相互独立,定义矩阵分式函数:

证明由引理1 可知,只需验证分式函数满足EBD条件(1)、(2)、(3)即可。事实上,由模型(12)中Pb(C)的定义易证EBD条件(1)、(2)、(3)都成立。
在实际问题中,待聚类数据集中通常含有异常点和高斯噪声。考虑令第i 个数据样本点:


将式(15)代入式(14)有:

则数据样本点在被噪声和异常点干扰情况下可表示为:
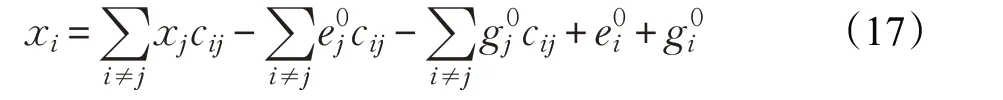
即:
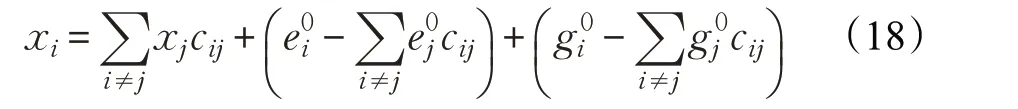
写成矩阵的形式为:
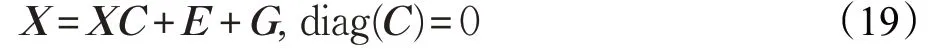
其中E、G 的每一列向量ei、gi被定义为:

因此,考虑到噪音的情形,对模型(12)进行优化,可变为:
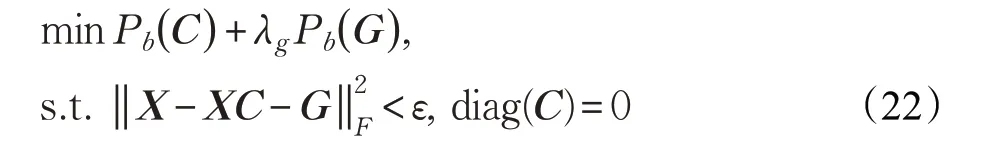
3.2 模型求解
本节对基于分式函数约束的稀疏子空间聚类模型式(22)进行求解。首先,利用正则化方法,模型(22)可写为:
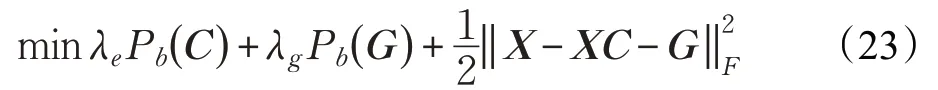
然后,利用交替方向迭代算法对式(23)进行求解。先将问题转换为以下两个子问题(24)和(26),再利用FP迭代阈值算法对式(24)、(26)进行求解如下所示。
固定Gk,对C 求极小:
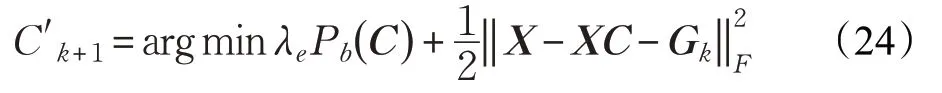
再令

固定Ck+1,对G 求极小:

式(24)求解,该式可以转化成标量最小化问题,应用定理1给出的分式迭代阈值算法的迭代格式,将变量代入迭代格式中即可求得。
式(26)求解,可知该式存在闭合解为:

其中,Ω 为分式函数约束最小化运算符,则G 可通过FP迭代阈值算法获得,和式(24)求解方法一致,由定理1中的FP阈值迭代格式可求出。
综上所述,通过交替方向迭代算法求解FPSSC模型进行聚类时,首先利用更新规则得到最优解,然后构建亲和矩阵,最后应用谱聚类来得到聚类结果。具体实现过程如算法1所示。
算法1FPSSC算法
输入:数据点矩阵X=[x1,x2,…,xN],参数λe、λg。
初始化:Ck=Gk=0,μ=10-6,ρ=1.1,ε=10-8。
1.通过式(24)、(25)、(26)分别对变量Ck、Gk进行更新
2.更新参数:μk+1=min{ρ μk,μmax}
4.获得最优化问题的解(C*,G*)
6.谱聚类
输出:每个数据点的聚类结果。
3.3 算法收敛性分析
本节中,讨论FPSSC算法的收敛性。本文利用交替方向迭代方法对模型(22)进行求解,由于Pb( C )和Pb( G )都是非凸函数,因此不能从理论上保证上述算法的收敛性。但是,本文进行了大量实验,实验结果显示,实际应用中的FPSSC 在最优化问题的求解中通常都能很好地收敛。
4 实验结果与分析
将本文提出的FPSSC 算法与当下比较流行的几个基于谱聚类的子空间聚类算法进行实验比较,选择人工数据集、Extended Yale B人脸数据库、Hopkins155运动分割数据集这3 个流行的标准数据库进行对比实验。上述数据库的部分样本图像如图3 所示。在人工合成数据集上,本文用算法分割的精确度衡量其性能的优劣;在Extended Yale B 人脸数据库和Hopkins155 运动分割数据集上,采用子空间聚类错误率衡量其性能的优劣,其中定义:

图3 数据库的部分样本图像
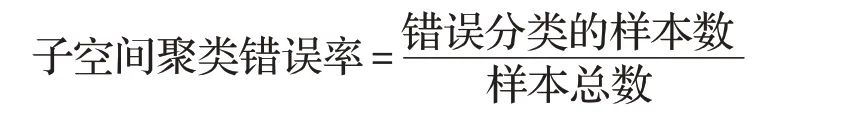
可见,子空间聚类错误率越小,其聚类结果越好,算法性能越优。本文实验环境为Microsoft Windows 10,采用Inter®Core™i5-3230M CPU@2.60 GHz处理器,4 GB内存的联想G500笔记本电脑。
4.1 人工数据集
本文构建一个人工数据集用来比较不同子空间聚类算法的性能。依据类似于文献[23]和[24]的方法,创建5 个相互独立的子空间Si⊂R200(i=1,2,3,4,5),子空间的基能够利用Ui+1=TUi,1 ≤i ≤4 得到,其中T 是一个随机矩阵,U1是一个100×4 维数的随机正交矩阵。故每个子空间的维数是4,外围空间的维数是100。首先,通过Xi=UiQi,1 ≤i ≤5 从每个子空间中选取20个100维的数据点向量,这里Qi是一个4×20的随机矩阵且矩阵内每个元素皆在(0,1)之间均匀分布,故可以得到5 个子空间样本为20×100 的数据点矩阵X=[X1X2X3X4X5]。然后,在数据点矩阵中随机选取20%的数据点向量加入高斯噪声,这里的高斯噪声分布服从均值为0,方差为0.3‖ x‖(‖ x ‖表示选取的数据点向量)。最后,应用谱算法把数据点分成5 类同时比较每类方法分割的准确率。由于该人工数据集上仅加入了高斯噪声,故在此实验中取参数λg=0。
在本数据集上,将所提出的FPSSC 算法与经典的SSC、SR2,1、SR1和LRR 子空间聚类算法进行对比实验,其中SR2,1模型和SR1模型分别为:
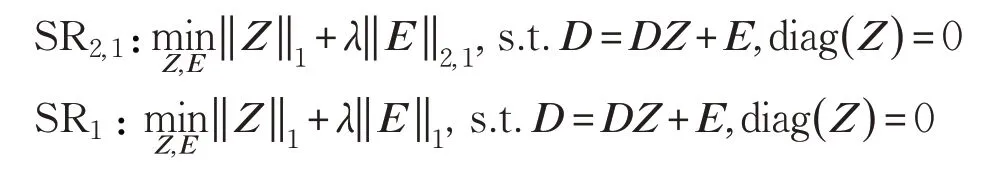

表1 不同算法中系数矩阵的稀疏度
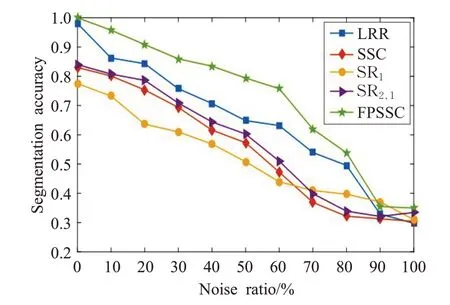
图4 不同算法在人工数据集上的分割精确度
图4 为各算法在该人工数据集上的运行结果。通过综合比较,可以看出本文的FPSSC对数据的分割精确度高于其他几种算法,表现出良好的性能。亲和矩阵可以影响算法性能的优劣,SSC、LRR、SR1和SR2,1同本文算法一致,都是先求取亲和矩阵,然后将亲和矩阵用于NCuts的谱聚类算法进行数据聚类。结合表1和图4可知,由于SSC、SR1和SR2,1皆是用1-范数作为目标函数,故获得的系数矩阵不够稀疏。然而本文的FPSSC用分式函数作为目标约束,通过调节分式函数中的参数b使得系数矩阵的稀疏度低于其他几种算法,获得了更好的稀疏性。另一方面,各算法在噪声的处理上有所不同,本文在处理噪声时使用Forbenius范数进行约束,表现出对高斯噪声较好的鲁棒性。可以看到随着噪声比率的增加,各算法的分割精确度都在下降,SSC和SR2,1精确度下降较缓慢,但是都低于FPSSC 的精确度,可见FPSSC受噪声影响较小,鲁棒性更好。SR1使用1-范数进行噪声约束,当噪声比率高于60%时其精确度相对稳定且高于SSC 和SR2,1,但FPSSC 的精确度仍然高于SR1算法。可见,本文的FPSSC算法通过调节分式函数的参数b 提高了模型的稀疏性,且在处理噪声时使用Forbenius范数对噪声进行有效约束,提高了模型的鲁棒性,使FPSSC表现出良好的性能。
4.2 Extended Yale B人脸数据库
Extended Yale B人脸数据库是用于测试子空间聚类算法的标准数据库,本文将所提算法应用到该数据库检验FPSSC的有效性。Extended Yale B人脸数据库采样了38 类灰度大小为192×168 的人脸,每类含有64 张处于不同光照下的人脸图像,本文将图像灰度转化为48×42 并使用2 016 维矢量化的图像作为一个数据样本。结合文献[25],本文将38类目标图像依次分为如下4 组:1~10、11~20、21~30 和31~38,其中前3 组中的每一组,本文实验采用所有可以选择的2、3、5、8、10个类别,对于第4 组,本文使用所有可选的2、3、5、8 个类别进行重复实验。为了验证本文算法的有效性,实验过程中将结果与当前性能较好的SCC[26]、LSA(Local Subspace Affinity)[27]、LRSC[28]、LRR、SSC 进行比较,实验结果如表2 所示,其结果中给出不同算法在取不同类别时,在Extend Yale B数据库进行重复实验过程中聚类错误率的平均数和中位数。
由表2 可知,在不同的聚类类别下,FPSSC 聚类结果的错误率要低于其他几种算法,具有更好的性能。在该人脸数据库上,SCC和LSA通过搜索数据点的全局和局部结构构建亲和矩阵,其模型自身具有局限性,导致它们聚类错误率偏高,表现出最差的性能。观察到SSC和LRR作为经典的基于稀疏表示和低秩表示的子空间聚类算法,其能够获得比LRSC算法相较更低的聚类错误率,而且随着聚类类别数的增加,SSC 表现出比LRR更优秀的性能。然而,本文所提的FPSSC算法,由于获得更为稀疏的系数矩阵并对两个噪声项进行了有效约束,所以在聚类类别不同的情况下,平均聚类错误率均低于SSC和LRR算法,且在类别数逐渐增大时,要明显低于其他算法的聚类错误率。故FPSSC 提高了聚类结果的准确性和稳定性,算法性能优于其他几种算法。
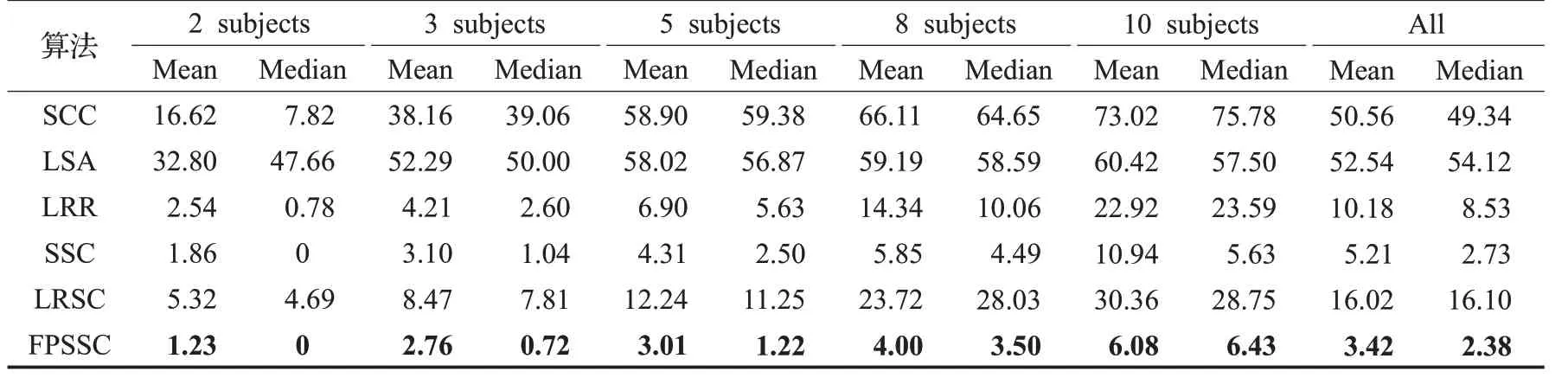
表2 不同算法在Extended Yale B人脸数据库上的聚类错误率%
4.3 Hopkins155运动分割数据集
Hopkins155 数据集是一个具有代表性的标准视频数据集,广泛地应用于聚类实验中。运动分割是指根据场景中的不同运动对一个包含多个运动物体的视频序列进行分割。对视频中每一帧的N 个特征数据点进行提取和跟踪,特征数据点堆叠获得的一个2F 维向量(F为视频的总帧数)对应特征轨迹,因此,运动分割就是根据其基本的运动分离这些运动轨迹的问题。本文实验采用的Hopkins155 运动分割数据集中包含155 个视频序列,其中122 个视频序列含有2 个运动,每个序列30帧,具有266个特征轨迹;35个视频序列含有3个运动,每个序列29帧,具有398个特征轨迹。每个视频帧的子空间低于三维。参照文献[29]的实验设置,本文首先应用主成分分析算法对运动轨迹进行有效降维,将运动轨迹从2F 维降到4n(n 为子空间的数量)维,然后分别将子空间聚类算法应用于该数据集中执行算法程序,结果中表3 是2F 维数据点下聚类错误率的均值和中位数,表4是4n 维数据点下聚类错误率的均值和中位数。

表3 不同算法在Hopkins155运动分割数据集2F维数据点下的聚类错误率%
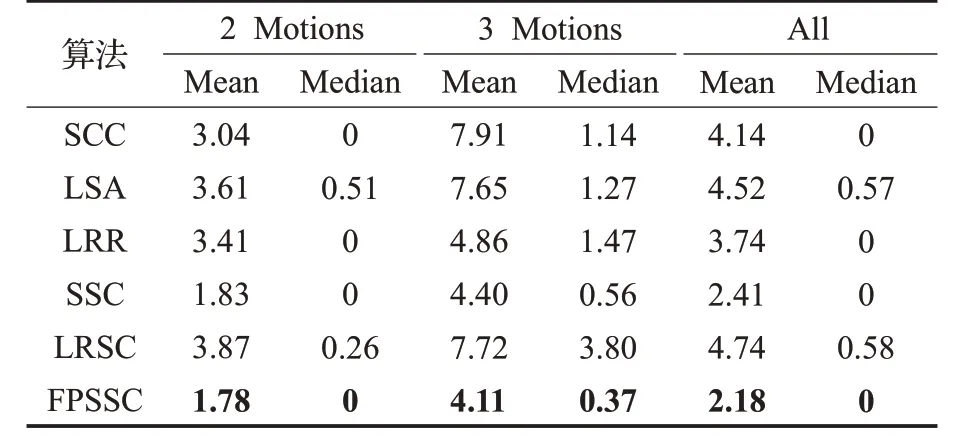
表4 不同算法在Hopkins155运动分割数据集4n维数据点下的聚类错误率%
表3和表4分别为运动轨迹在2F 维和4n 维下的聚类结果。分析表中的聚类结果可以看出,FPSSC 在4n维数据点下的聚类错误率低于其他几种算法,具有较优的聚类结果;在2F 维数据点下,由于该数据集中类别为2或3,相比其他数据集类别较少,因此在分式函数的约束下,稀疏性在一定程度上会加重数据的局部性,导致在维数较大的情况下,本文算法与SSC 的性能相差无几,算法性能没有表现出明显的优势。但是值得注意的是,相较于SCC、LSA、LRR和LRSC,FPSSC算法表现出了很好的性能,而且在2 个运动时,虽然FPSSC 的聚类错误率相较SSC略高,但是随着聚类类别数增加到3个运动时,FPSSC 的聚类错误率却要明显低于SSC,说明随着类别数的增加,FPSSC 能够获得较低的聚类错误率。综上所述,本文的FPSSC算法能够有效的捕获数据的结构信息,在实际应用中获得较优的聚类结果。
4.4 参数选择
本节分析参数选择对FPSSC 算法性能的影响。具体地,影响FPSSC 算法性能的参数主要包含3 个:调节分式函数的参数b、平衡噪声项的参数λe和λg。本文利用交叉验证方法对参数进行选择,分别在Extended Yale B 人脸数据库类别为10、Hopkins155 运动分割数据集类别为3 的情况下进行实验。其中参数b={10,20,30,40,50,60,70,80,90,100},λg={10-4,10-3,10-2,10-1,100,101,102},λe={0,0.02,0.04,0.06,0.08,0.10,0.12},通过搜索不同参数值对算法性能的影响进行评价。图5表明参数b 取值在70~90范围变化时,算法的聚类错误率较低,算法相对稳定。图6和图7分别表明参数λe和λg变化时对聚类错误率的影响,因所选数据库受噪声影响程度不同,故平衡参数λe和λg的最优取值也不同。
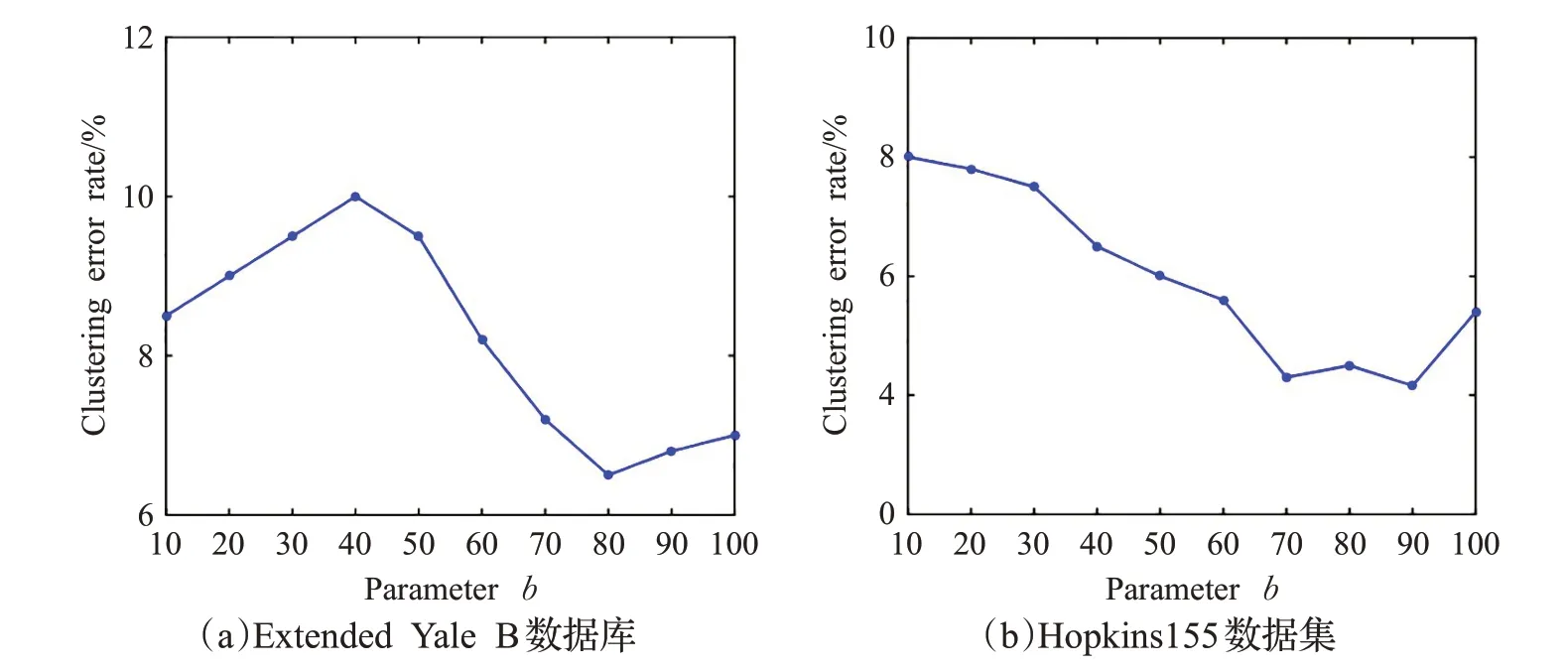
图5 参数b 对聚类错误率的影响
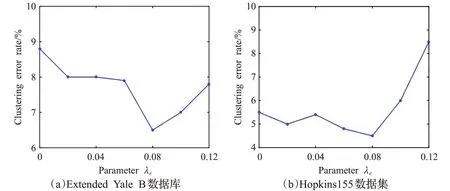
图6 参数λe 对聚类错误率的影响

图7 参数λg 对聚类错误率的影响
综上所述,基于分式函数约束的稀疏子空间聚类方法在人工数据集、Extended Yale B数据库和Hopkins155数据集上表现出良好的性能。可以看到,相较其他的子空间聚类算法,由于分式函数能够逼近0-范数,具有良好的稀疏性,采用分式函数进行约束能够准确地刻画高维数据点的数据结构,因此该方法在子空间聚类中取得了更好的聚类结果。
5 结束语
本文提出一种基于分式函数约束的稀疏子空间聚类算法。不同于经典的SSC算法,FPSSC使用分式函数替代0-范数作为目标函数以提高系数矩阵的稀疏性,并证明了分式函数获取的系数矩阵具有块对角结构,能够有效地表现出数据点之间的关系,准确捕获数据的子空间结构。同时,针对含噪声的情况,对异常点噪声同样使用分式函数约束作为正则项,增加模型的稳定性。再运用交替方向迭代方法对模型进行求解,构建亲和矩阵,最后使用谱聚类算法进行聚类。在3个数据集上的实验结果表明,本文提出的FPSSC算法在系数矩阵稀疏性和聚类准确率上均表现出较好的性能,算法更加有效。下一步的研究重点,将对复杂含噪数据的数据结构进行研究,给出其成功恢复下的理论保证。

