关联交叉口子区的信号优化控制方法
曹 洁,张丽君,侯 亮,陈作汉,张 红
1.兰州理工大学 计算机与通信学院,兰州730050
2.甘肃省制造业信息化工程研究中心,兰州730050
1 引言
交通堵塞的日渐严重,不仅影响城市的正常运转,而且降低了人们的日常工作效率和生活质量[1]。城市路网由大量道路和交叉口组成,路网密度和车辆的增加会使交通流在各个交叉口和路段间的关联性更加明显。因此,路网交叉口群的有效控制是解决当前“城市病”问题的有效手段。
国内外有关交叉口群的控制研究包括关键交叉口控制、干线控制和区域控制三个方面[2]。目前,基于优化算法对城市路网的区域控制是交通控制的一个重要研究内容。遗传算法作为一种自适应优化算法,因其具有搜索效率高的特点,广泛应用于交叉口的信号优化控制问题中。文献[3]提出了一种考虑双向绿波的干线相邻交叉口相位差优化控制方法,采用改进的遗传算法进行求解并实现了交通干线的协调控制。文献[4]提出了面向多个宏观基本图(MFD)子区的边界协调控制方法,建立了以整个路网旅行完成流率最大、平均行程时间和平均延误最小的多目标边界协调优化模型,并通过自适应遗传算法对多目标函数进行求解。文献[5]采用基于遗传算法的多目标优化方法,提出了信号控制多层模糊控制模型,以平均延误和停车次数作为优化目标,采用遗传算法中的随机权重方法来进行该模型的多目标综合优化,给出了各模型参数的计算方法和优化步骤,最后进行了仿真试验。文献[6]以区域路网机动车总延误为优化目标,建立了非机动车影响条件下的区域交通信号控制优化模型,优化了信号周期时长、绿信比和相位差等参数,并利用遗传算法求解模型。
综上所述,基于遗传算法的路网交叉口信号优化控制研究取得了一定进展,但仍然存在以下问题:(1)遗传算法在解决优化问题时,其自身存在早熟收敛的缺点;(2)路网交叉口的信号控制过程中,缺乏对交叉口间关联性问题的考虑,使得交通控制与交通流在各个交叉口间的动态变化相脱离。本文针对现有研究的不足,提出基于改进遗传算法的关联交叉口信号优化控制方法。
2 交叉口子区信号控制优化
城市路网中的交叉口在静态因素和动态因素间都存在关联性,交通拥堵往往通过一个交叉口蔓延到另一个交叉口[7]。因此,将关联性强的交叉口作为一个整体进行信号优化控制是解决城市路网交通拥堵的有效措施。本文方法的具体流程如图1所示。
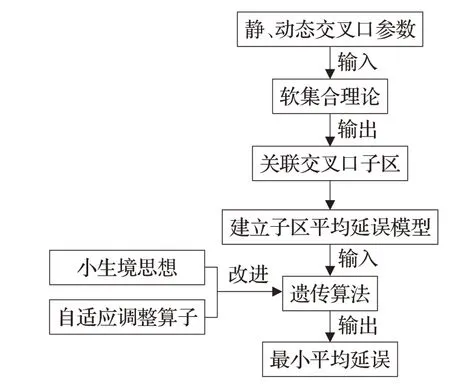
图1 关联交叉口子区的优化控制流程
2.1 基于软集合的关联交叉口划分
软集合理论作为一种处理不确定性问题的数学工具,其在实际决策问题中取得了一定的进展[8]。本文将相邻交叉口关联性的强弱看作一个决策问题,综合考虑路网交叉口动静态因素对交叉口关联性的影响[9],选取交叉口间距影响因子DIF、周期影响因子CIF、交通流影响因子VIF、交通流离散影响因子PIF 和排队长度影响因子QIF作为子区划分的决策集。由于以上5个因子对关联交叉口子区划分的影响程度不同,因此,本文根据实际路网的交通情况确定关联交叉口划分的阈值如表1所示。
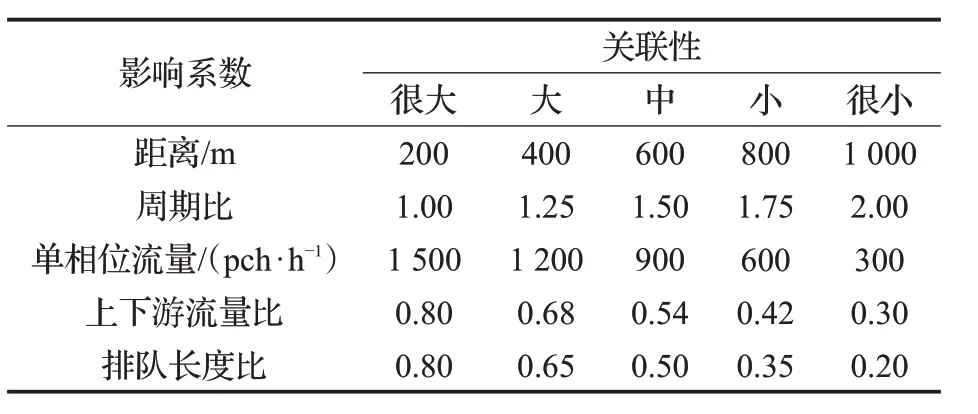
表1 关联交叉口划分的阈值
以上是路网交叉口间能否进行关联控制的建议值,利用表1建立相邻交叉口的关联度矩阵,并通过信息熵计算出受划分阈值影响的DIF、CIF、VIF、PIF 和QIF 的权重大小,具体步骤如下所示。
(1)建立关联度矩阵:

(2)归一化处理:
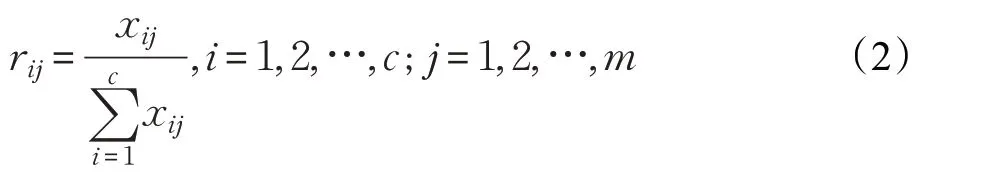
(3)计算熵值:
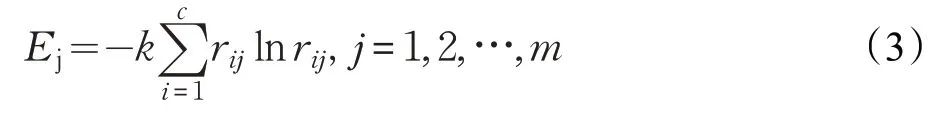
式中,c(c=5)为交叉口间关联度的类别数,归一化系数定义为,取负号保证熵值为正。
(4)计算决策因子的偏差度:

(5)确定各个因子的权重:
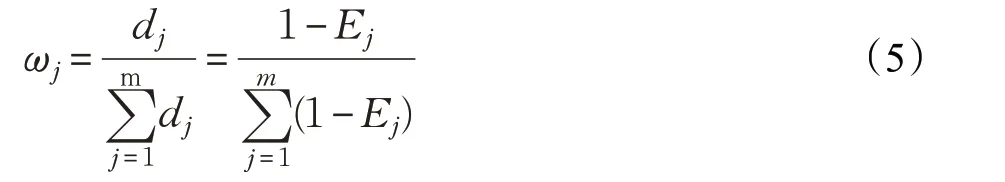
通过以上步骤得出交叉口间关联性影响因子的权重向量为ω={ω1,ω2,ω3,ω4,ω5}。再结合软集合理论实现路网交叉口群的关联交叉口子区划分,其中,U={S1-S2,S2-S3,S3-S4,…,Sn-1-Sn}表示所有相邻交叉口的一个集合,n 表示路网的总交叉口数,E={DIF,CIF,VIF,PIF,QIF}表示路网中交叉口的关联度属性组成的参数集合。因此,基于软集合理论的关联交叉口子区的划分步骤如下:
步骤1 输入相邻交叉口关联度决策因子(U,E);
步骤2 输入权重向量ω={ω1,ω2,ω3,ω4,ω5};
步骤3 输出各个相邻交叉口的协调系数值CF。
2.2 改进遗传算法的关联交叉口控制
2.2.1 算法改进思路
遗传算法作为一种模拟自然进化过程搜索最优解的方法,是由美国Michigan 大学的教授Hollend 在1962年首次提出[10]。虽然遗传算法广泛应用于交叉口的信号优化控制问题中,但算法自身易早熟且交叉概率Pc和变异概率Pm的取值直接影响到算法的收敛性[11]。针对以上问题,本文提出改进的遗传算法来优化关联交叉口的平均延误。具体的改进有以下两个方面:
(1)小生境
种群进化过程后期大量个体集中于一个极点,导致种群多样性降低[12]。为了解决该问题,本文在遗传算法中引入小生境技术的共享函数,其原理为:共享函数能够体现出个体之间的相似程度,利用其调整群体中个体适应度可以达到维护群体多样性的目的,从而使算法根据调整得出的适应度进行选择运算。具体表现为当两个个体关系越密切,则共享函数值越大;反之,共享函数则越小。
个体i 与个体j 之间的基于基因型的共享函数Sh(i,j)计算公式如下:
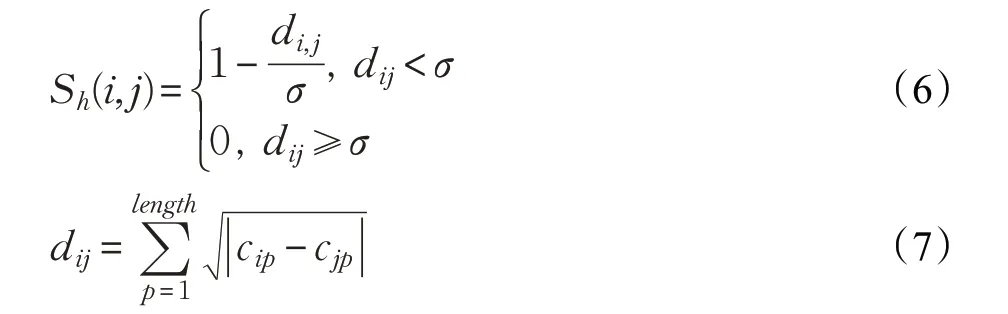
其中,cip、cjp分别表示个体i 与个体j 上的第p 个基因,dij表示个体i 与个体j 间的海明距离,σ 是小生境大小半径参数。个体i 调整后的应度比率Rs(i)为应度比率R(i)除以小生境数mi,公式如下:

(2)遗传算子自适应调整
在遗传算法的改进研究中证实[13],较大的Pc(0.5 <Pc<1)和较小的Pm(0.001 <Pm<0.05)对成功使用遗传算法求解问题来说是必要的,较大的Pc促进了个体间的交叉概率,较小的Pm防止个体特性遭到严重破坏。因此,为了改善遗传算法早熟的缺陷,结合群体适应度比率的分布特征,动态调整交叉概率Pc和变异概率Pm的公式如下:
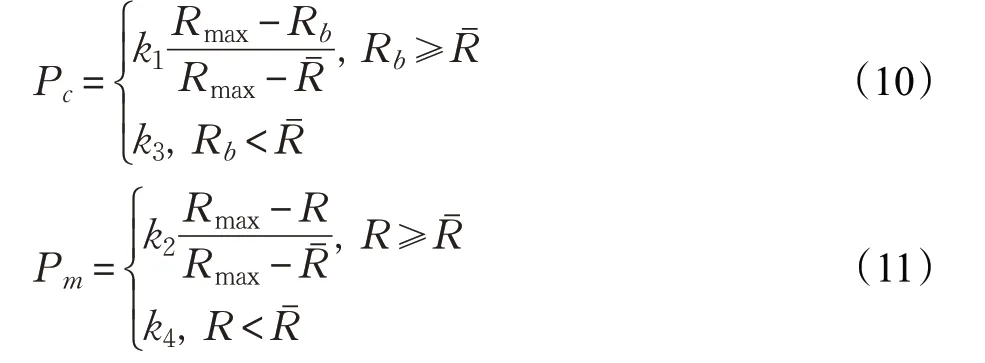
其中,Rmax、R、Rb、Rˉ分别是群体的最大适应度比率、群体的平均适应度比率、两个交叉个体中较大的适应度比率和当前个体的适应度比率。在现有研究的基础上,得出总结:0 ≤ki≤1(i=1,2,3,4);当k2=0.5,k4=0.5 时,算法在求解过程中能够避免过早地陷入局部最优;当k1=1,k3=1 时,算法中不大于平均适应度比率的所有个体能够进行交叉运算。两个交叉个体中较大的适应度比率的取值越接近Rmax,交叉概率越小;当且仅当取值等于Rmax时,交叉概率为0,从而保证了优秀个体的稳定性。
2.2.2 交叉口子区的计算模型
路网中交叉口运行效率的提高是衡量交通信号有效控制的标准,即最大限度地缩短交叉口的延误时间[14]。因此,本文以路网子区的实时交通数据为基础,以子区内交叉口的平均延误时间为目标函数,通过优化得出最小平均延误时间,并确定最佳绿灯配时方案。
车辆的延误采用韦伯斯特延误模型[15],公式如下:
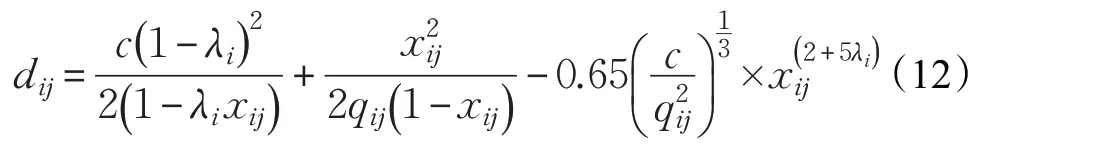
交叉口的平均延误时间公式如下:
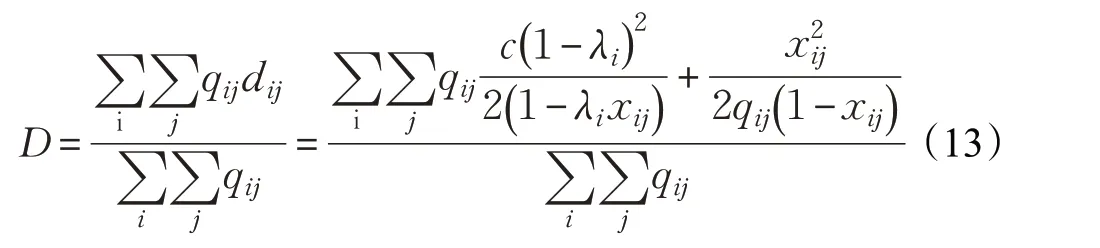
其中,dij是第i 相位、第j 流向下车辆的平均延误时间,单位为s;c 为信号周期时长,单位为s;qij为第i 相位、第j 流向下的车辆到达率,单位为pch/h;xij为第i 相位、第j 流向下的饱和度;λ 为第i 相位的绿信比。
目标函数为平均延误时间最短,即L=min D。
路网的约束条件为:
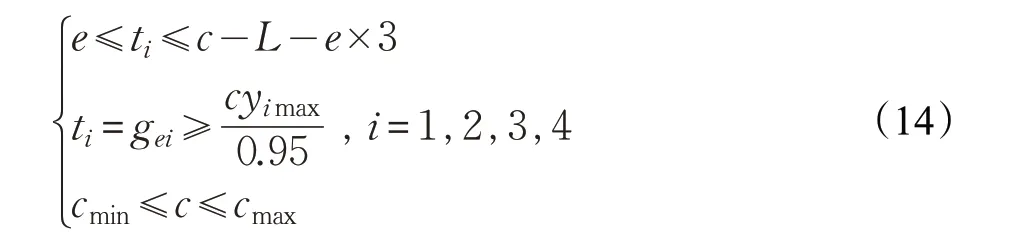
其中,e 为每个相位的最短绿灯时间,取e=10 s;ti为第i 个相位的有效绿灯时间,单位为s;c 为交叉口的实际信号周期;L 为总的损失时间,单位为s;gei为每个相位的绿灯时间;yimax为最大流量比,为了避免交叉口的某些进口道中出现堵塞现象,各相各进口道饱和度最大值选取0.95;cmin、cmax为交叉口的最小周期与最大周期。
2.2.3 改进遗传算法的函数优化求解
步骤1 染色体编码:利用实数编码,选取路网子区中各交叉口绿时差与周期的比值为基因构造染色体并形成种群。为了保证基因的变化范围能够均匀地初始化种群,种群的大小设为150。
步骤2 确定适应度函数:由于本文对交叉口的平均延误时间函数进行优化求其最小值,所以将F()i=Cmax-O(i )作为适应度函数,其中,F(i )为第i 个个体的适应度;O(i )为第i 个个体的目标函数值;Cmax为O(i )的最大估计值。
步骤3 遗传操作:首先,采用轮盘赌与精英策略相结合的方式进行选择操作;然后,采用共享机制的小生境技术并自适应地调整遗传算子进行交叉操作和变异操作;最后,本文选取最大进化次数为50 时,终止算法的运算。
3 实验结果与分析
3.1 实验方案
为说明关联交叉口子区的信号优化控制方法的有效性,本文选取由19 个交叉口组成的城市路网进行实验。路网的实测数据包括静态数据和动态数据,其中,静态数据是交叉口间的距离,动态数据是以15 min为周期,以单交叉口为对象,采集其信号周期、单相位流量、上下游流量、排队长度、饱和度。通过采集以上数据,利用软集合理论对路网进行关联交叉口子区划分,并利用改进的遗传算法对划分的子区进行信号优化控制。
3.2 关联交叉口子区的划分
实验将路网交叉口群的实测数据和熵权法计算出的权重向量ω={0.285,0.070,0.285,0.130,0.230}共同输入Matlab软件进行实验仿真,得出如表2所示的软集合。
根据表2 中软集合计算出的相邻交叉口的关联协调系数值,结合路网复杂的交通情况,本文将协调系数在0.76以上[16]的相邻交叉口划分在一个子区,得到关联交叉口子区的划分结果如图2所示。
由图2可得,通过软集合理论输出的协调系数将路网交叉口群划分为9 个关联交叉口子区,分别是A、B、C、D、E、F、G、H、I。其中,一个子区的交叉口数并不是固定的,例如子区A由S1、S5、S9这三个交叉口构成,子区I由S17单个交叉口独立构成。
3.3 两种算法的控制效果对比
图2路网中关联交叉口子区划分后,利用改进的遗传算法对子区内交叉口的平均延误进行优化,为了验证划分方法的合理性,本文选取S3-S4子区进行实验仿真。
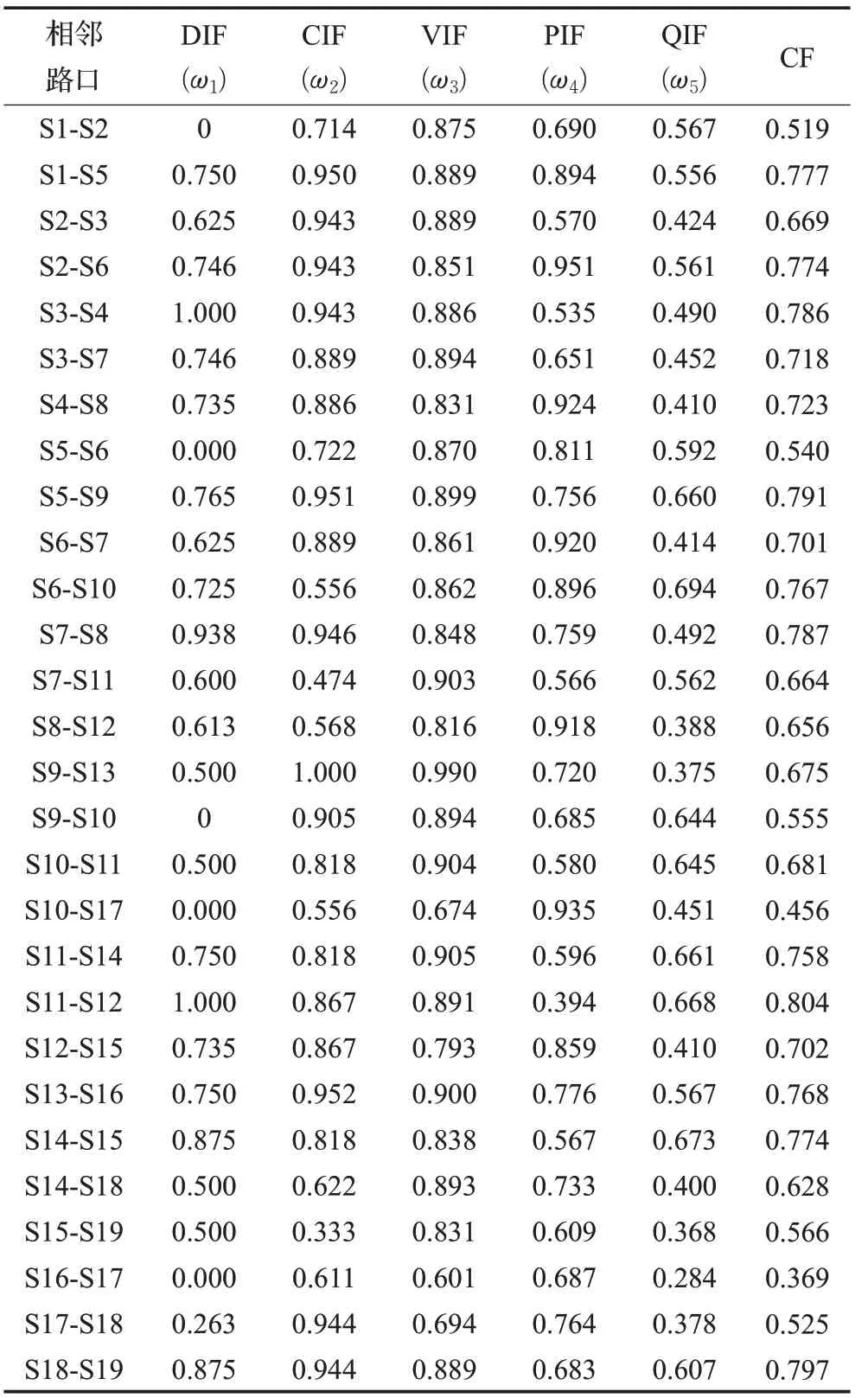
表2 关联交叉口软集合

图2 关联交叉口子区的划分结果
由于在关联交叉口S3-S4子区中,交叉口S3的交通流量和饱和度均较大,因此,选择S3的交通参数作为实验参数。S3 是一个典型的四相位(a.东西直行;b.东西左转;c.南北直行;d.南北左转)交叉口,实验选取S3 早晚两个高峰时段、一个正常非高峰时段各1小时的数据进行仿真,实测S3各进口道1小时的交通流数据如表3所示。其中A、B、C分别为早高峰流量、晚高峰流量、正常非高峰流量(单位为pch/h)。
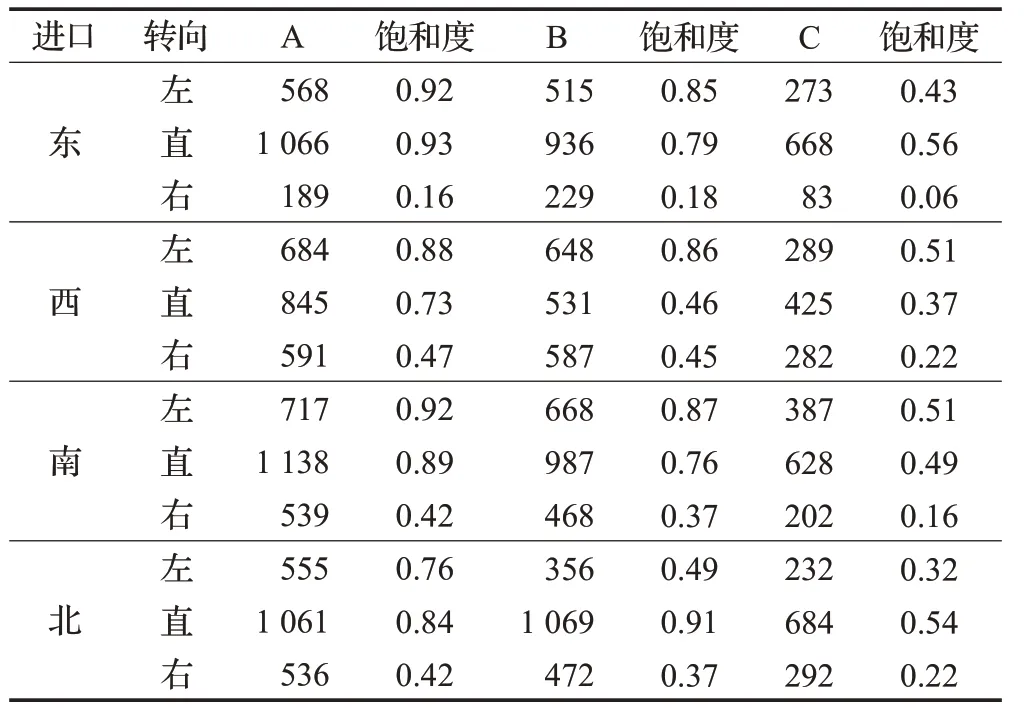
表3 S3交叉口早晚高峰、非高峰流量统计表
3.3.1 目标函数的对比
采用Matlab 仿真平台分别利用改进的遗传算法和遗传算法对S3-S4 子区的平均延误函数进行仿真。本文通过大量实验最终确定仿真过程的参数:初始种群大小为150,最大进化代数为50,传统遗传算法的交叉概率Pc和变异概率Pm分别取0.9和0.1,交叉口的最小周期和最大周期分别取80 s 和150 s,周期损失时间为10 s。将早晚高峰和正常非高峰时段三种交通情况的数据进行实验仿真,得到两种算法在S3-S4子区中的优化效果,分别如图3、图4、图5所示。
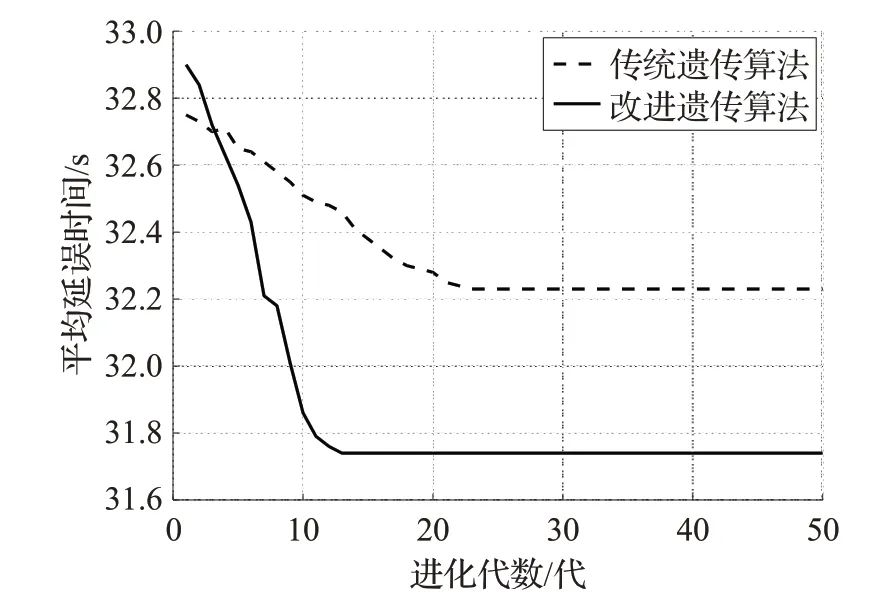
图3 早高峰进化过程对比图
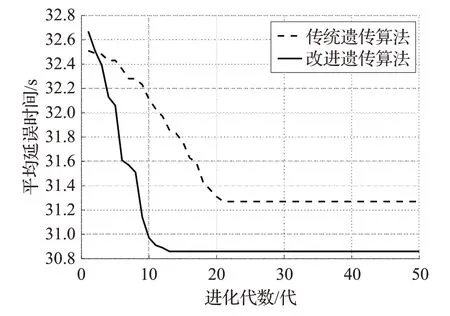
图4 晚高峰进化过程对比图
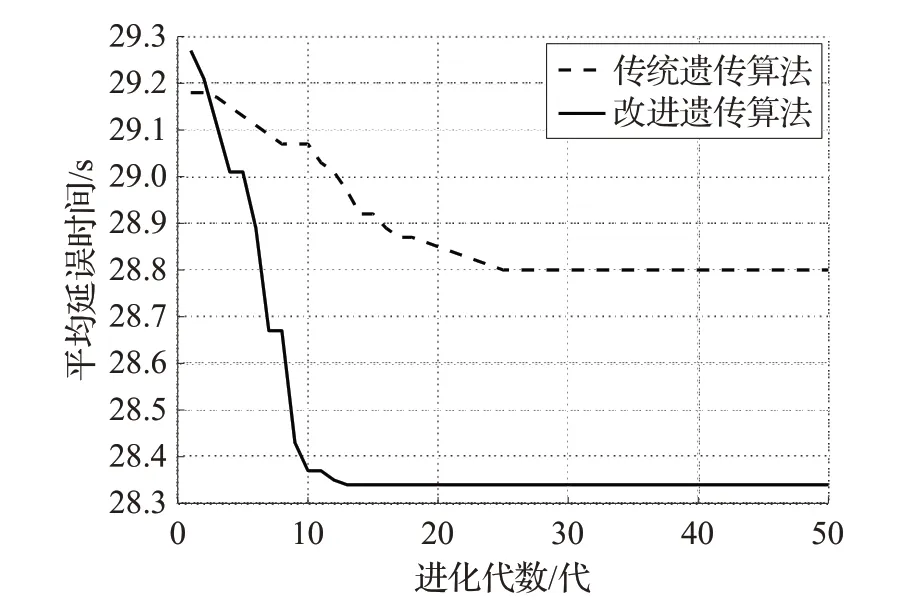
图5 正常非高峰进化过程对比图
由图3、图4、图5可以看出,改进的遗传算法在早晚高峰和正常非高峰时段三种交通情况的平均延误时间分别减少了0.49 s、0.41 s、0.56 s,进化代数分别减少了10代、9代、12代。由此可得,本文方法具有较快的收敛速度和更好的控制效果,从而得到最佳绿灯配时方案,使得关联交叉口子区的平均延误时间最短。实验结果表明,本文利用小生境技术的共享函数并自适应调整遗传算法的算子能够有效提高算法的收敛性,且减少了交叉口的平均延误时间。
3.3.2 配时方案的对比
通过改进前后遗传算法对S3-S4子区早高峰、晚高峰、正常非高峰三个时段的交通数据进行交叉口平均延误时间的优化,得出最小延误所对应的最优配时方案如表4所示。其中,GA为简单遗传算法,IGA为改进遗传算法。
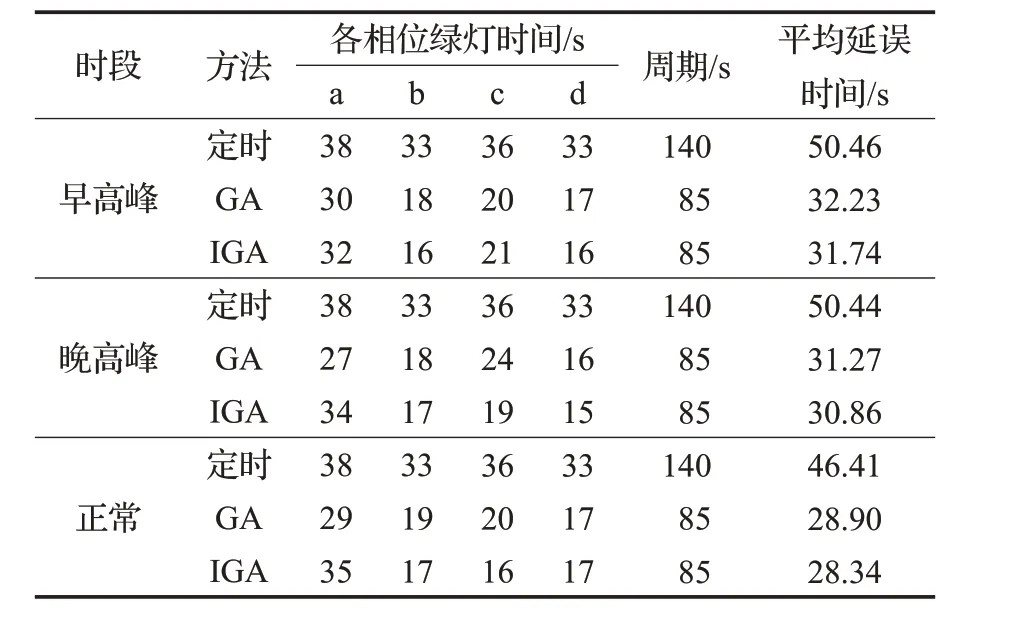
表4 两种算法的配时方案对比
由表4得知,改进遗传算法和简单遗传算法在以上三个时段优化得出子区交叉口的平均延误时间均小于定时控制,表明两种算法的配时方案(周期为85 s)效果明显优于定时控制(周期为140 s),且周期符合80 s <C <150 s。同时,与遗传算法优化得出的配时方案相比,改进遗传算法对各相位分配的时长具有更好的分离度,相位一、三的绿信比相对较高,更符合表3中车流量(直行>左转>右转)的规律。由此可得,本文改进遗传算法对交叉口信号配时更加合理,使得子区的平均延误时间更短。
3.3.3 适应度的对比
适应度函数是衡量群体中个体好坏的标准,其能够驱动遗传算法进行演化和自然选择。本文将目标函数的最大估计值与目标函数之差作为适应度函数。对比简单遗传算法和改进遗传算法的最佳适应度函数曲线如图6所示。
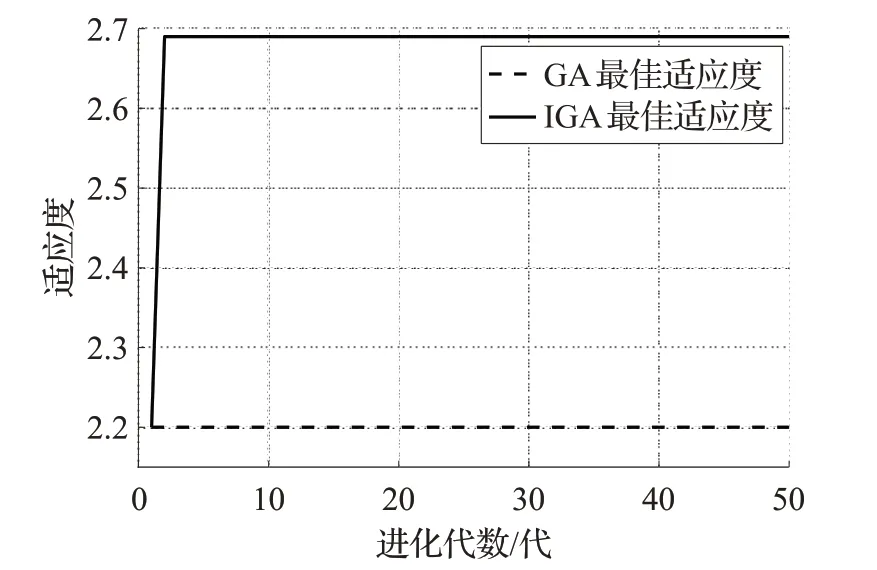
图6 适应度函数的对比
由图6可以得出,改进遗传算法的适应度函数值大于简单遗传算法的适应度函数值,这表明改进算法采用小生境技术的共享函数并自适应地调整算法的交叉概率和变异概率,其收敛性优于简单遗传算法,且不易陷入局部最优。
3.4 子区划分前后的对比
为了验证本文信号优化控制方法的合理性,利用改进遗传算法分别对单交叉口和关联交叉口子区进行实验仿真。实验以平均延误时间作为衡量指标,关联子区选取交通流量和饱和度较大的交叉口参数作为实验参数,单交叉口选取各自的交通流量和饱和度作为实验参数。在该实验中,选取路网中A、C、G三个子区进行实验仿真,得到相应的交叉口子区平均延误时间,结果如表5所示。
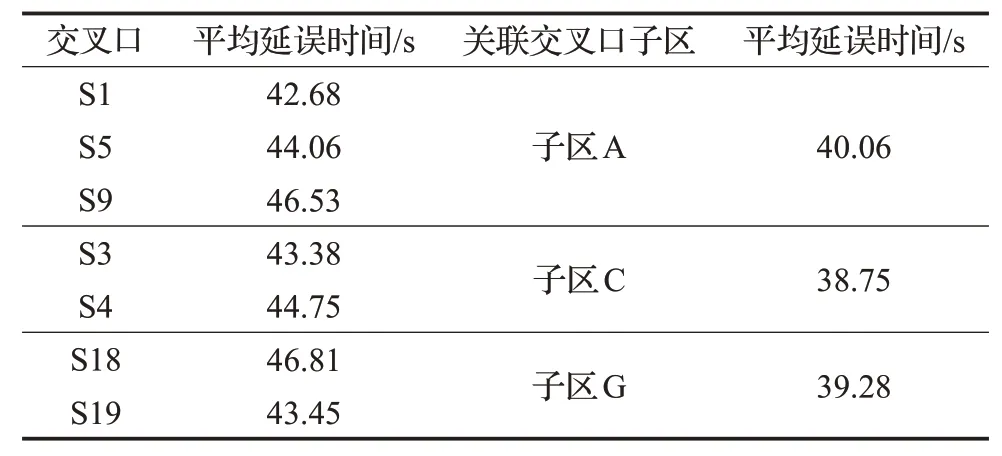
表5 划分前后仿真结果对比
仿真结果表明,关联交叉口子区的控制效果与交叉口单独控制的效果相近。本文将路网交叉口群划分为关联交叉口子区进行信号优化控制,减少了路网交叉口群的平均延误。因此,考虑交叉口关联性的信号优化控制方法具有实际应用价值。
4 结束语
本文提出一种关联交叉口子区的信号优化控制方法,以解决城市路网复杂的交通情况和遗传算法易早熟收敛的问题。该方法在软集合理论划分关联交叉口子区后,利用小生境技术并自适应调整遗传算法的算子对其进行改进,将改进算法应用到关联交叉口子区进行信号优化控制。通过采集的路网数据在Matlab 仿真平台上进行验证。实验结果表明,本文方法合理划分了关联交叉口子区,且改进算法在子区信号优化控制中能够准确、快速地寻找到全局最优解,降低交叉口的平均延误时间。

