快速收敛参考独立分量分析方法

贾雁飞，杜艳丽，赵立权

1.北华大学 电气与信息工程学院，吉林 吉林132013

2.东北电力大学 电气工程学院，吉林 吉林132012

1 引言

独立分量分析方法是一种解决混合信号分离的新颖方法，它仅仅只利用原始信源信号之间的非高斯，而且相互统计独立的特性，从观测到的原始信号的混合信号中分离出所有的原始信号，相对现有的信号分离方法结构更简单，效果更好。参考独立分量分析是为了解决独立分量分析中不能单独分离出某个或者多个感兴趣的信源信号而提出来的。相对独立分量分析，参考独立分量分析在某些应用环境中，更适合实际应用。例如语音信号提取中，可能对其中部分语音信号感兴趣，如果采用独立分量分析方法，则必须提取出所有的语音信号，然后后期再从提取的语音信号中找出感兴趣的语音信号，整个过程比较繁琐，计算量较大。采用参考独立分量分析，仅需要将拟提取的感兴趣的语音信号的特征融入到参考独立分析中，则可以直接提取出感兴趣的语音信号，尤其是当原始信号数量较多的时候，采用参考独立分量分析方法提取信号相对基于独立分量分析方法具有明显的优势。

目前参考独立分量分析方法已经被应用于图像处理、语音信号提取、通信信号提取等多个领域[1-5]。现有的参考独立分量分析主要从降低误差、提高抗噪声能力、提高信号分离的成功率以及收敛速度等角度进行了研究[5-11]。虽然可以利用收敛阶数更高的牛顿迭代方法的对其代价函数进行优化[12-13]，有效降低了算法的迭代次数，但是算法的复杂度也增加很大，因此收敛速度提高的程度受限。

为此，本文对现有牛顿迭代方法进行了研究和分析，提出采用结构简单，且具有阶收敛速度的牛顿迭代方法[14]对预处理后的参考独立分量分析代价函数进行优化，推导出收敛速度更快的参考独立分量分析方法。

2 参考独立分量分析

参考独立分量分析从独立分量分析演进得到的，其代价函数类似独立分量分析的代价函数，其代表函数表达式如下[15]：

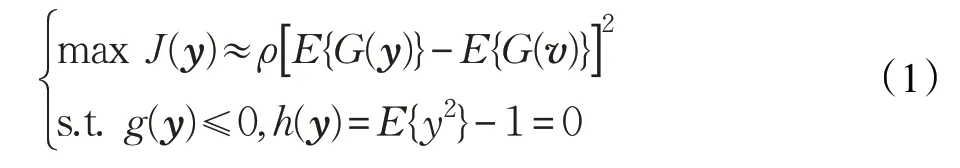
式中，G 是一个非线性函数，其表达式与独立分量分析中给出的非线性函数表达式一样，y 是估计出的信源信号，v 是与估计出的信源信号y 具有相同均值和方差的高斯随机信号，ρ 仅仅是一个值为正的常数，J(y)即为独立分量分析的代价函数；g(y)是参考独立分量分析算法融入到独立分量分析算法中的一个约束函数，用来度量估计出的信源信号与参考信号之间的相似度，h(y)是用来约束估计出的信号方差，使得估计出的信源信号方差为1，避免每次估计出的信源信号具有不相同的方差。

参考独立分量分析算法在代价函数中引入松弛因子，将式（1）中的不等式约束条件转变成等式约束条件，其表达式如下：

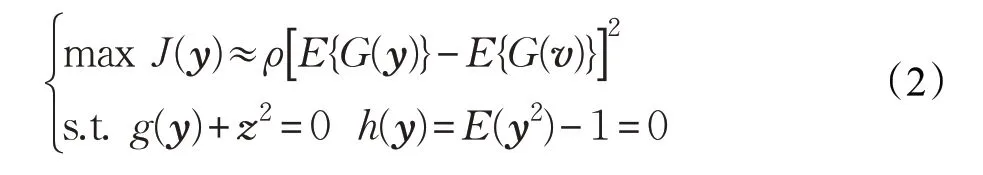
采用拉格朗日乘法方法将上式约束条件转化成如下表达式：

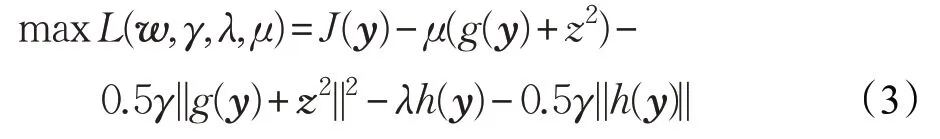
式中，y=wTx 是分离信号，w 是分离向量，x 是是观测观测信号，γ 是惩罚因子，μ 和λ 为拉格朗日乘子。对其上各变量进行优化，可以将（3）式转换成如下表达式：

参考独立分量分析采用传统的牛顿迭代方法对（4）式进行求解，求解过程中的分离矩阵迭代表达式如下式所示：

式中，η 是固定的步长参数，Rxx是观测信号的自相关矩阵，k 是迭代过程的当前迭代次数，和分别是L(w,γ,λ,μ)对当前迭代分离向量wk的一阶和二阶导数。其具体表达式如下：

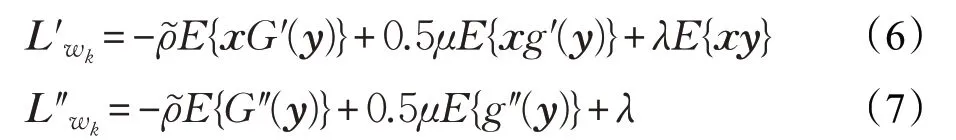
式中，G′(y)是非线性函数G(y)的一阶导数，G″(y)是非线性函数G(y)的二阶导数。g′(y)是非线性函数g(y)的一阶导数，g′(y)是非线性函数g(y)的二阶导数。参数μ 和λ 的迭代更新公式表示如下：

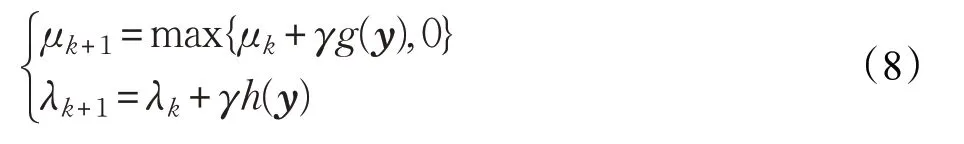
3 改进的参考独立分量分析

根据式（5）可知，参考独立分量分析在分离向量迭代过程中需要计算观测信号的相关矩阵的逆矩阵，并且每次迭代需要计算该逆矩阵与其他矩阵的乘积，增加了算法的计算量。为此，本文借鉴文献[7]的思想，采用白化的方法对观测到的混合信号进行预先处理，假设观测信号为z，则经过白化处理后的信号可以表示为：

式中，B=Σ-1/2U，Σ 为观测信号的协方差矩阵的逆矩阵进行特征值分解得到的特征值矩阵，U 为特征向量矩阵。通过白化预处理方法使得处理后的信号均值为零，方差矩阵为单位矩阵，因此只要限制白化后信号的分离向量为正交矩阵，即可实现原算法约束分离信号的信号方差为1的限制。因此经过白化处理后，参考独立分量分析的代价函数数学表达式可以表示成如下的形式：式中，各参数的表达含义与式（2）相同。同样采样拉格朗日方法对上式进行处理可得：

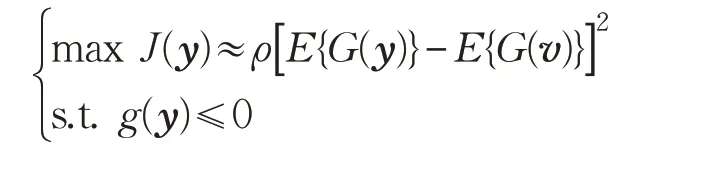
式中，w0是初始化的分离向量，w1是在初始化值的基础上得到的对分量向量的初始估计向量：

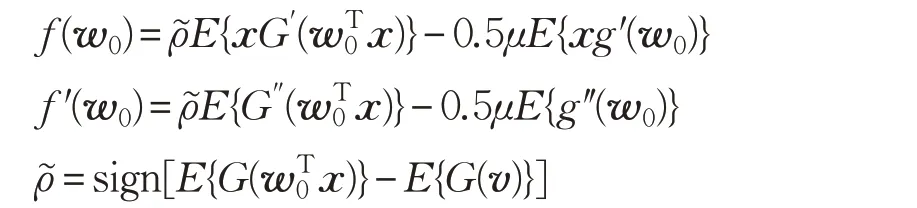
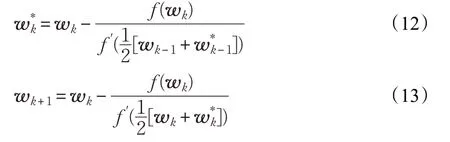
式中，f()和f′()分别是式（10）对分离向量w 的一阶和二阶导数。

本文提出改进方法中式（11）与文献[7]的分离向量迭代更新公式相同，但是本文仅仅将其作为初始化分离向量的重新初始化，分离向量迭代更新公式采用式（12）和（13）进行。公式（11）也就是文献[7]算法需要分别计算法一次代价函数一阶导数和二阶导数，假设导数的计算量相同，在忽略其他除法和加法的计算量的基础上（导数的计算量远大于其他计算量），文献[7]一次迭代的计算量为2n。本文提出的方法初始化时的计算量为2n，第一次迭代的计算量为3n，第二次迭代过程中由于已经存储前一次，则其计算量为2n，以此类推，本文算法m 迭代的计算量同样为2n。也就是说本文算法的每次迭代的计算量与文献[7]算法的计算量相同（除了第一次迭代），随着迭代次数的增多，总的计算量二者基本相同。但是，本文算法采用阶收敛的牛顿迭代方法，相同条件下，收敛时需要的迭代次数更少，因此在每次迭代计算量相同的条件下，本文算法从理论分析上来看需要的运算时间更短。

4 实验结果与分析

为验证本文所提出的算法有效性，采用概率密度分别为亚高斯分布、高斯分布、超高斯分布的信号作为信源信号，信源信号均值为0，方差为1。混合矩阵随机产生。

图1是5个信源信号，信号所有的采样点均为5 000个点，但是由于采样较多时随机信号难以分辨，所以随机信号仅画出前500个采样点。图2是信源信号的混合信号。

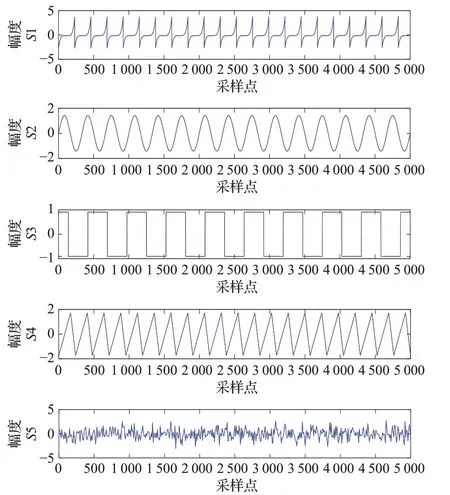
图1 信源信号

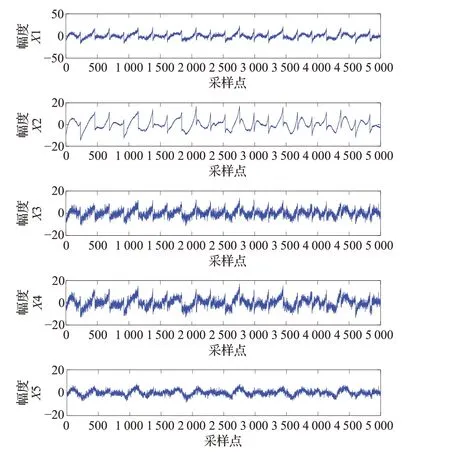
图2 混合信号

图3 是对图1 信源信号S1 和S2 的估计；图4 是对图1信源信号S3、S4 和S5 的估计。

图3 分离信号1

对比图3、图4 和图1 可以看出，两种算法都是有效的，都实现了对信源信号的估计。表1 给出了两种算法的定量分析。误差采用独立分量分析中最为常用的性能指标函数进行度量，其具体表达式如（14）所示：

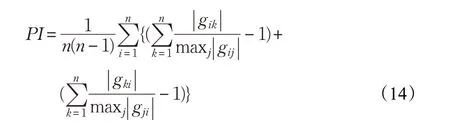
式中，g 代表的是分离矩阵与混合矩阵乘积得到的全局矩阵中的元素，n 时是全局矩阵的维度，理想条件下，性能指标为零，该指标的值越小，表示算法的误差越小。从表1 可以看出，本文算法与文献[7]算法性能指标一致，但是平均运行时间远远小于文献[7]算法。

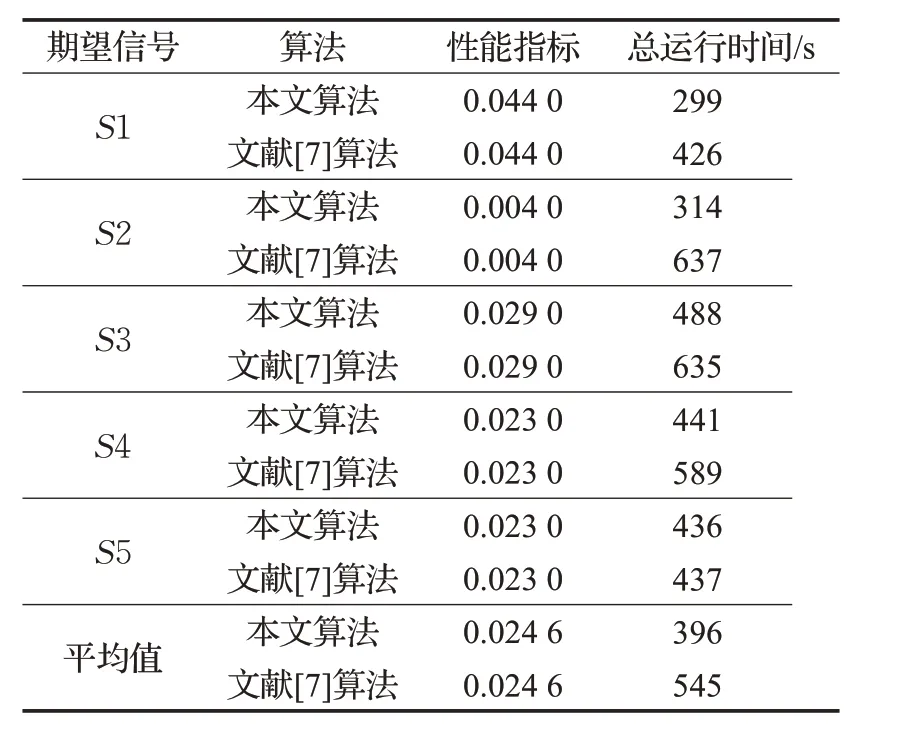
表1 算法平均性能分析

5 结束语

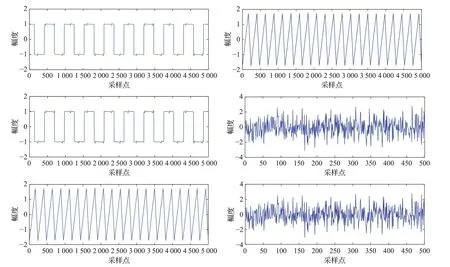
图4 分离信号2

本文从参考独立分量分析收敛速度角度出发，提出采用计算复杂度低、收敛阶数较高的牛顿迭代方法对预处理后的混合信号的代价函数进行优化，推导出收敛速度更快的参考独立分量分析方法。本文改进后的算法无论是提取亚高斯、高斯和超高斯信源信号都是有效的，而且相对已有方法的性能指标是相同的，但其收敛速度明显快于已有方法。