基本不等式在高次及不定方程(组)中精彩演绎*

福建省厦门第一中学 (361003) 王淼生福建省厦门市第三中学 (361006) 叶泽军

我们熟知以下不等式链：

当且仅当a1=a2=…=an时，①等号成立．

我们将上述①称为基本不等式．

基本不等式看似简单，其功能极其强大！正如姜伯驹院士感叹：“最简单的东西，往往也是最本质、最基本的东西，通过对简单的把握，建立思维体系，通过推理，得出的结果往往是惊人的，这就是数学思维，是科学精神．”拙文[1]—[11]从不同侧面展示了基本不等式在不等式求解、代数式最值(范围)，特别在不等式证明等方面的应用．其实，基本不等式的应用并不仅仅局限于不等式，遵循哲学对立统一的观点，基本不等式在方程(组)中大有作为．尤其对那些令人棘手的不定方程(组)或者高次方程(组)，如果运用基本不等式并恰当好处利用其等号成立的条件，在“不等式”与“等式”之间架起一座桥梁，则可获得独辟蹊径的解法．本文通过具体案例，呈现基本不等式在解决高次及不定方程(组)中的精彩演绎．

1.案例呈现

(1)单元高次方程

案例1求方程(x2006+1)(1+x2+x4+…+x2004)=2006x2005的实数解的个数．

解：由方程结构特征容易发现：倘若上述方程有实数解，那么一定是正数解，否则方程右边为负数，而左边恒为正数．

(2)多元高次方程

案例2 若x，y，z，w∈R，求解下列方程中的x，y，z，w的值：(22x+1)(22y+2)(22z+4)(22w+8)=128·2x+y+z+w．

(3)单元无理方程

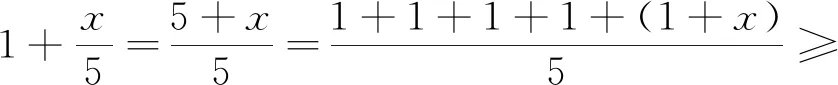
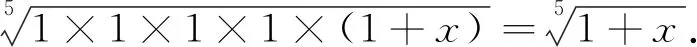
1=1+x，即x=0时等号成立，故原解方程的解为x=0．

(4)多元无理方程

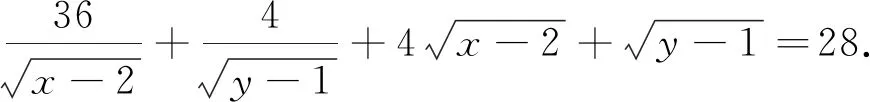
(5)结构相似方程组

案例5 求以下方程组的所有解：

解：观察发现x≥0，y≥0，z≥0．当x=y=z=0时，显然满足上述方程组．当x>0，y>0，z>0时，上述方程组中三式相乘得到

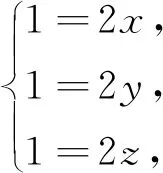
(6)结构不同方程组

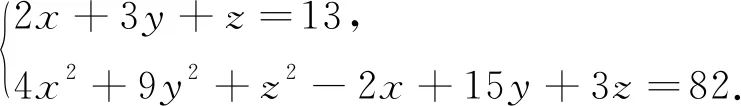
以下与案例7的解法相同，请看案例7：

(7)转化为方程组

证明：设长方体一个顶点上的三条棱的棱长分别为a，b，c，则有a+b+c=3，a2+b2+c2=3．

上述案例7涉及立体几何，其实基本不等式在平面几何中也有类似的功能，请看案例8：

案例8 在ΔABC中，ha，hb，hc分别为三边上相应的高，r为三角形内切圆的半径，且满足ha+hb+hc=9r．试确定ΔABC形状．

将它们代入已知条件ha+hb+hc=9r得到

事实上，①式本身相当于隐含条件，具有制约功能，请看以下案例9.

(8)验证方程组

案例9 设x、y、z∈R，且

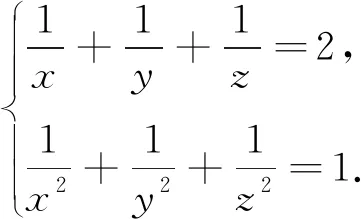
2.案例评析

上述案例1、案例2均属于高次方程，案例3、案例4属于无理方程，倘若按照常规思路解答，其过程异常复杂；案例6源自1992年“友谊杯”国际邀请赛一道试题，与案例5比较，案例6则属于结构完全不同的方程组，如果案例6采取常见的代入消元手段，则显得特别困难；将案例6适度变形就与案例7本质完全相同；案例7、案例8属于基本不等式在立体几何与平面几何方面的应用；案例9源自某市一道竞赛试题．从表面上看，专家给出的解答(即错解)似乎无懈可击，但从正解就发现根本不存在这样的实数x、y、z，究其原因在于命题专家没有关注这两个方程组之间还有着致命的制约条件(即基本不等式)，从而导致这两个方程相互矛盾！这就提醒我们在命制与不定方程相关的问题时，应该首先考虑到制约条件，否则极易出现看似正确但实际矛盾的试题.

上述9个案例展示了基本不等式①在解决不定方程(组)及高次方程(组)中的精彩演绎．其实，基本不等式在解析几何、三角、数列等知识模块中亦有上佳表现．尤其将基本不等式引入待定系数后，其功能更是如虎添翼(详见文[11]).

3.心得体会

“基本”蕴含基本事实，凸显简捷之美，显示基本条件，具有创新功能，折射事物本源，贯穿事情始终．事实上，上述①基于一个最为基本的代数事实：任何实数的平方均为非负数：

若x∈R，则x2≥0，试想还有比这个事实更为基本、更为简捷的吗？正如罗增儒教授指出，任何实数的平方均为非负数，这是实数一个非常深刻、带有本源性的性质，已成为实数大小关系的一个基本出发点，因而基本不等式①也自然带有实数大小关系的本源性特征，因此上述①在整个不等式知识体系中具有举足轻重、不可或缺的基础性、本源性地位，因此新课标教科书将上述①称为“基本不等式”是实至名归、恰如其分．

事实上，上述①的初衷，也是最基本、最经典的应用就是为了解决“和定求积最大值；积定求和最小值”问题，这正是很多人喜欢将上述①称为“均值不等式”的缘故．尽管上述①功能强大，但毕竟是一个工具；尽管“均值不等式”称号形象生动，但名字仅仅只是体现其功能．若将上述①称为“重要不等式”，看似进一步强化了其在不等式乃至整个高中数学中的作用，甚至不惜冠以“重要”二字，但这仅仅只是一个重要结论，一个结果而已．新一轮课改的精髓在于学会知识与技能的同时，充分展示其过程和方法，进而培养情感态度及价值观，这就是为何将“三维目标”作为基础教育追求的目标所在，这才是数学教育的真谛，这正是为何新课标教科书将上述①的“名字”改为“基本不等式”的真正原因所在．看似一个名字的改变而已，实则凸显了教材及主编的理念，那就是将上述①作为整个不等式知识的一个起始点、一个发源地，凸显一个“过程”的开始．遗憾的是，很多教师没有注意到这一名字的改变，在课堂上依然开口、闭口还是“均值不等式”、“重要不等式”．谁不知，一个名字的改变体现了教材编写者用心良苦，承载着教材主编多少希翼与梦想，又凝聚数学专家多少辛劳与心血．

当然，柯西不等式、排序不等式等著名不等式在解决解决方程(组)同样妙不可言．无论是基本不等式，还是柯西不等式、排序不等式等著名不等式，其关键在于充分挖掘等号成立的条件，使之成为“等”与“不等”之间的纽带，最大限度地将基本不等式的功能发挥得淋漓尽致，从而得到简捷、优雅的解答，正如克莱因感叹“一个精彩巧妙的证明，精神上近乎一首诗．”这就是数学方法恩赐于数学教师独有的高雅的精神享受！这就是数学王国对数学教师最高的奖赏！这就是数学迷宫吸引无数人为之疯狂的魅力所在！