三跨连续波形钢腹板箱梁桥力学特性研究
曹洪亮,李淑琴,刘洪成,路本生,杨震宇
(1.山东高速高广公路有限公司,山东 济南257399;2.合肥工业大学汽车与交通工程学院,安徽 合肥230009)
随着预应力混凝土梁(PC梁)的普及,桥梁建设发展迅速。为了满足桥梁跨径不断增加的需求,减轻大跨度预应力混凝土桥梁上部结构质量是桥梁结构技术革新的一个重要目标[1]。波形钢腹板PC组合箱梁充分发挥了混凝土和波形钢腹板材料的优点,减轻自重,提高了桥梁的跨越能力[2-5]。文章以某三跨连续波形钢腹板预应力混凝土箱梁桥为工程背景,针对桥梁上部结构,采用迈达斯软件建模,计算各受力阶段的应力、位移等,验证该桥型的优越性[6-8]。
1 设计说明
该桥为上下行分离式三跨连续梁桥,跨径布置为47m+52m+47m。主梁为单箱三室波形钢腹板PC组合桥梁。双向标准6车道,桥面净宽为2×12.25m,设计速度为120km/h,桥梁设计汽车荷载为公路-I级×1.3。该桥采用现浇预应力混凝土波形钢腹板连续箱梁,箱梁顶宽16.85m,底宽11.85m,翼缘悬长2.5m。梁高3.2m,顶板厚25cm,底板厚22cm,箱梁腹板采用波形钢腹板,波形钢腹板采用1600型等高截面直腹板(见图1),腹板钢材种类为Q345qc,厚度为12mm,工厂加工成一个标准段长3600mm的波形钢腹板。为了减弱侧向变形,并且通过横隔板达到转向的目的,各跨设置了三道厚20cm的横隔板,并设置人孔为检修施工用。
剪力连接件设计对结构承载能力有显著影响。在设计过程中,默认剪力全部由腹板承担。波形钢腹板的剪切屈曲稳定性是研究的重要内容,同时也需要对其剪应力进行验算。本桥采用双开孔波折板连接件连接形式将波形钢腹板与混凝土连接,采用焊接剪力钉+开孔钢板构成的剪力键将波形钢腹板与底板连接,具体见图2。

图2 剪力连接件型式
2 有限元模型建立
文章采用MIDAS Civil软件建模[9]。通过扩展单元建立全桥跨度的各个单元。将全桥共划分为311个节点,310个梁单元,单元长度分配为10×0.05+290×0.5+10×0.05m。渲染模型如图3所示,预应力钢束布置和边界条件等按实际情况建立。

图3 波形钢腹板PC组合箱梁的几何模型图
全桥采取满堂支架施工,整个成桥过程分为三个步骤:
步骤1:加载自重,且张拉预应力钢束N1、N2;
步骤2:加二期荷载——桥面铺装;
步骤3:施工阶段结束,即将进入成桥阶段。
3 计算结果
3.1 应力验算
该桥截面应力验算的点的位置1、2如图4所示。

图4 截面应力验算位置
3.1.1 施工阶段的应力验算
由于波形钢腹板几乎承担所有剪力,故在进行承载力验算时只进行正截面承载应力验算。
这里的短暂状况是指施工阶段,接下来将对施工阶段的3个步骤依次进行验算(3个步骤的内容见节2详述)。
由于从加载二期恒载到施工结束即将进入成桥阶段是一个连续的短暂过程,故直接对施工阶段末期即即将交付使用前的混凝土正应力进行验算。

图5 施工结束交付使用前主梁应力
施工结束交付使用前主梁应力见图5。在施工阶段末期,主梁上缘位置1处为全截面受压,最大压应力,位于边跨支座附近,满足《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2004)的要求:
3.1.2 使用阶段的应力验算
根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》的要求,计算时采用标准组合(所有荷载分项都为1.0):1.0×箱梁自重+1.0×预加力+1.0×沉降+1.0×二期恒载+1.0×徐变+1.0×移动荷载+1.0×整体升温。标准组合下主梁应力见图6。

图6 标准组合作用下主梁应力
在标准组合工况下,主梁上缘位置1处为全截面受压,最大主压应力σcp=10.41MPa;主梁下缘位置2处为全截面受压,最大主压应力σcp=12.67MPa,均满足《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2004)的要求:σcp≤0.60fck=0.6×32.4=19.44MPa。
3.1.3 正截面抗裂验算
①作用效应短期组合

图7 短期组合作用下主梁应力
根据《公路桥涵设计通用规范》计算时采用作用效应短期组合:1.0×箱梁自重+1.0×预加力+1.0沉降+1.0×二期恒载+1.0×徐变+1.0移动荷载+0.8整体升温。短期组合作用下主梁应力见图7。
作用效应短期组合工况下,主梁上缘位置1处为全截面受压,最大压应力σsc=10.41MPa,位于中跨跨中;主梁下缘位置2处最大压应力σsc=12.67MPa,虑到最易开裂截面即为拉应力最大截面,故对出现拉应力最大的跨中截面进行验算,σst=≤0.7ftk0.7×2.65=1.855MPa,满足《公路钢筋混凝土及预应力混凝土桥涵设计规范》的要求。
②作用效应长期组合
根据《公路桥涵设计通用规范》,计算时采用作用效应长期组合:1.0×箱梁自重+1.0×预加力+1.0沉降+1.0×二期恒载+1.0×徐变+0.4移动荷载+0.8整体升温。
在长期组合工况下,主梁上缘位置1处为全截面受压;主梁下缘位置2处全截面受压,满足《公路钢筋混凝土及预应力混凝土桥涵设计规范》的要求。
综上所述,长征桥的正截面承载能力、正应力和正截面抗裂验算合格。鉴于波形钢腹板箱梁的受力特性,在抗剪方面只需对波形钢腹板进行验算即可。
3.2 波形钢腹板抗剪承载力计算
3.2.1 腹板剪切屈曲稳定性验算
该桥波形钢腹板PC组合箱梁中所用的波形板形状如图1所示。几何尺寸如下:
q=1600mm,b=430mm,d=370 mm,
hr=2200mm,t=10mm
波形钢腹板PC组合箱梁的剪力主要由波形钢板承受,故对腹板的抗剪强度进行验算。
①局部剪切压屈曲强度
该桥的h取2750mm,则:
②整体剪切压屈曲强度
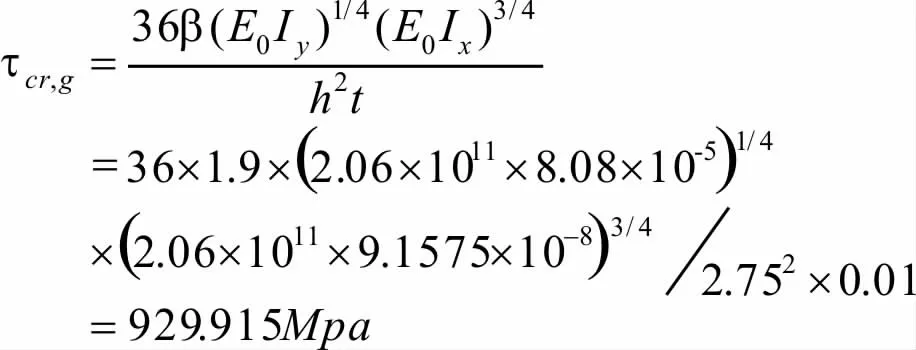
③合成屈曲强度
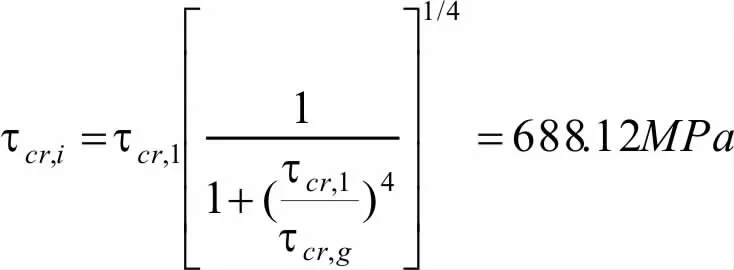
在荷载组合后的最不利状态下,梁的最大剪力Q=9725.4kN。每侧腹板所受的剪力T=Q/4=2431.4kN,每侧腹板所受的剪应力。
由τ<τcr,1,τ<τcr,g,τ<τcr,i,局部剪切压屈服强度、整体剪切压屈服强度、合成剪切强度都比每侧腹板受的剪应力高的多,这表明剪力屈曲不会导致破坏。
钢腹板中的剪应力大致是按均匀分布,其弯曲剪应力τ平行于剪力Q,因此,剪应力的计算公式为,τ=,其中,h为波形钢腹板的竖向高度,w为波形钢腹板的总厚度。计算得到的最大剪应力为63.80MPa,小于Q345钢材规范要求的120MPa。
综上所述,波形钢腹板的抗剪强度满足设计要求。
3.3 竖向挠度验算
该桥在短期组合下的挠度形状图如图9。

图9 短期组合下的挠度形状图
边跨最小挠度为-8.0mm,中跨最大挠度为19mm,挠度验算如下。
根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》规定,预应力混凝土受弯构件的长期挠度值,在消除结果自重产生的长期挠度后梁式桥主梁的最大挠度处不应超过计算跨径的1/600。
对于边跨,反拱4.798mm,已完全满足要求,不需设置预拱度。对于中跨,挠度长期增长系数ηθ=1.425,则跨中截面在荷载短期效应组合并考虑荷载长期效应影响下的长期挠度为4.379×1.425=6.240mm,在消除自重产生的长期挠度后为6.240-13.865=-7.625mm<mm=50mm,也满足要求。
4 结论
文章针对某波形钢腹板PC组合连续箱梁桥建立模型,对波形钢腹板箱梁结构的受力特性进行了分析,得到了施工阶段和成桥阶段支座的支撑反力,同时验算了单项荷载作用下的弯矩、剪力和挠度。
对该桥进行了三类正应力方面的验算,包括短暂状况的正截面抗裂验算、正应力验算和持久状况的法向压应力验算,此外还进行了竖向挠度验算和波形钢腹板抗剪承载能力验算,对于应力图上出现的最不利荷载位置的验算,都满足相应规范要求。
波形腹板预应力混凝土组合箱梁桥,使混凝土抗压和波形钢腹板抗剪的优点得到了充分体现。同时,其强度、刚度、延性、抗震性和预应力传递效率的提高,能够满足桥梁跨径不断增大的需求。随着国内对这种结构的深入研究,波形腹板预应力混凝土组合箱梁桥将会在我国的桥梁建设中得到广泛地应用。

