自适应预处理的AMBTC图像压缩

张茗茗，周 诠，呼延烺，刘娟妮

(中国空间技术研究院西安分院空间微波技术国家级重点实验室，西安 710000)

0 引言

随着多媒体技术的飞速发展，产生和传输了大量的视频和图像信息，数据量急速增大，而数据内部存在很强的冗余性，这就意味着降低压缩带来的冗余度的必要性[1]。在JPEG、JPEG2000、HEVC等算法中，不仅文件大小明显减少，而且计算复杂度也大大提高。在航天航空数传系统中，由于硬件资源有限，开发特别复杂的图像压缩算法需要很大的硬件开销，而AMBTC在保证图像质量的前提下，计算复杂度低，且具有固定的压缩比，非常适合低成本的卫星数据传输。

绝对矩块截断编码(Absolute Moment Block Truncation Coding，AMBTC)是由Mohammed等人[2]首次提出的。根据平均值将每个块中的数据分割成两部分，用高平均值和低平均值表示像素。它是一位自适应量化器，保留小块的某些统计矩。Alrikabi等人[3]提出了一种基于AMBTC和Hadamard变换的压缩方法。具体来说，将图像分为两个区域，轮廓区域采用Hadamard变换编码，其余区域采用AMBTC编码。毫无疑问，这种方法有助于减少阻塞伪影，并以增加文件大小为代价充分保留纹理。Daga等人[4]提出了一种树分割的AMBTC方法，将每个16×16块分割成16×8、8×8、8×4或4×4块，这取决于方差和阈值的比较。尽管压缩率降低了，但图像质量却降低了，编码效率大大提高。Liu等人[5]提出了一种利用点扩散块截断编码分析计算效率与视觉伪影之间关系的新方法。尽管它具有良好的视觉质量、视觉感知能力和处理效率，但压缩率是无法固定的。Hui等人[6]应用遗传算法对上下中心进行了反复迭代。同样，PSNR可以达到最优，而复杂度大大提高。Balakrishnan等人[7]将AMBTC方法应用于遥感图像的彩色化。一般来说，RGB平面被转换成HSV平面，每一个H和S平面使用四分簇AMBTC编码，V平面使用基于双分簇或三分簇的AMBTC编码。原始图像可以被有效地压缩，但是每个平面上的块大小是不同的，其大小取决于平面上呈现的边缘信息。此外，Dacles等人[8]将AMBTC技术应用于音频数据。音频数据首先被分割并替换为高中心和低中心，并在哈夫曼编码中进行无损编码。基本信息得到保留，压缩率高，但由于音频数据本质上不是图像数据，因此PSNR不适合测量性能。Xiang等人[9]提出了一种多分组AMBTC算法。即使用四组，简单块以小尺寸编码，而复杂块以大尺寸编码。不同的阈值会导致不同的图像质量，因此每个图像中的最佳阈值可能会有所不同。Zhang等人[10]针对含有椒盐噪声的图像提出定点预估的压缩算法，进一步提升了图像质量，但是没有对噪声进行滤除，体现效果有限。

在原始图像存在椒盐噪声并且压缩比为4的前提下，上述算法不太可能获得良好的视觉质量。采用深度学习的对抗网络可以有效对缺失信息进行修复，但是需要大量的样本学习和计算开销，对硬件的要求较高，实际要求很难满足。因此，为了在这种情况下获得最佳的视觉质量，本文首先对噪声进行滤除，并对损毁的区域进行自适应的修复，然后采用AMBTC压缩。

1 AMBTC

AMBTC是一种高效的图像压缩算法，它保证了每个块的一阶矩和二阶矩不变。将m×n大小的原始图像分为4×4个不重叠的块。块中的平均值为M，并作为阈值。将不大于M的像素聚集到较低的平均值a，而将大于m的像素聚集到较高的平均值b。此外，将不大于M的像素替换为a并以1比特“0”中编码，而将大于M的像素替换为b并以1比特“1”编码。

(1)

其中p和q分别表示4×4索引块中“0”和“1”的个数。

块的比特流由8位a、8位b和16位块索引构成，因此压缩率(Compression Ratio, CR)等于16×8/32=4。基本信息得到了保留，AMBTC在计算量小的情况下可以获得良好的视觉效果。

例如，在如图1中所示，图1(a)是原始图像块，图1(b)是AMBTC图像块。块中像素{162，162，161，164，158，155，160，163，158，159，159，155，157}，M是160，a是157并编码为8比特“10011101”中，b是163并编码为8比特“10100011”中，块索引是“11111100001000”，最终比特流是“10011101101000011110000000”。

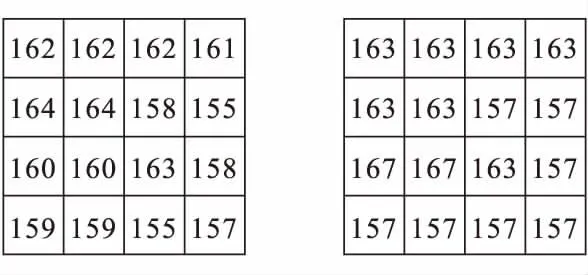
(a) (b)

2 本文算法

当图像受到椒盐噪声的污染时，图像的基本信息仍然能够保留，但是图像的显示效果下降很多，同时也不利于压缩。当噪声强度大于0.05时，AMBTC图像的PSNR值基本维持在20dB，即使采用全搜索的方法，提升非常有限，这就需要从图像本身进行修复。

椒盐噪声的像素值为0和255，一般图像中很少出现这两个值。当图像出现这两个值时，视觉对比相当明显。例如，在512×512的Lena图像中加入强度为0.2的椒盐噪声，统计像素直方图。直方图的比较如图2所示，图2(a)为原始图像的直方图，图2(b)为添加了椒盐噪声的图像的直方图。一般来说，直方图并没有很大的变化，但是0，255像素的出现频率比其他像素的出现频率要高得多。图像对比如图3所示，图3(a)是原始Lena图像，图3(b)是强度为0.2的Lena图像。受到噪声污染后，图像质量有了明显的下降。

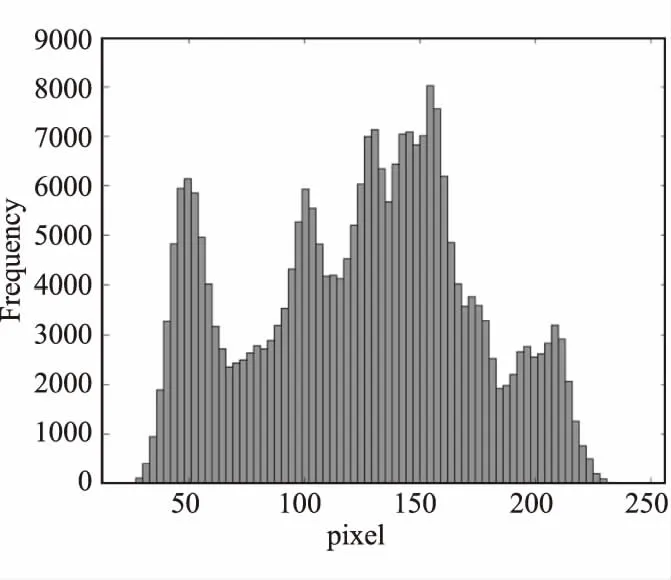
(a)

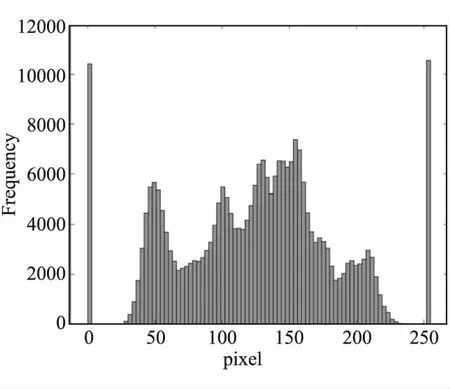
(b)

噪声是随机添加到图像中，即使强度很大，也不会出现大面积连通的缺损区域。图像内部仍然具有很强的相关性，可以利用周边有效像素插值预测。采用图像处理的膨胀算法可以解决这个问题，但是该算法主要考虑的是大的连通区域部分的修复，本文的主要对小区域的修复，利用欧式距离来判断邻域内有效像素的权重。距离越远的权重越低，距离越近的权重越大，这样充分利用了数据间的相关性。

(a) (b)

而距离与像素点是否为真实值有关，当像素点为真实值时，该点与所要预测的像素点较近，该点的真实性较高，权重应较大，当像素点为插值时，意味着该点真实值不存在，周边有效像素与所要预测的像素点较远，该点的真实性较低，权重应较小。权重w与像素点的关系为，

(2)

在图像的3×3邻域内，存在像素值的像素点个数为K，则预测结果m得到，

m=(w1×m1+w2×m2+…+wk×mk)/K(3)

其中，m1，m2，…，mK为已知像素，w1，w2，…，wK为相应的权重，有效像素点的个数K大于阈值N，才可以进行预测。

例如，在图4所示的图像块中，m8，m9，m13，m17四个像素点受到噪声的破坏，本文阈值N为6，即3×3邻域内，至少有6个已知像素点。这样，m8，m9，m17可以第一轮预测，而m13的有效像素点个数K为5，需要第二轮预测。

m8=(m2+m3+m4+m7+m12+m14)/6

m9=(m3+m4+m5+m10+m14+m15)/6

m17=(m11+m12+m16+m18+m21+m22+m23)/7

m13=(m7+0.8×m8+0.8×m9+m12+m14+

0.8×m17+m18+m19)/7.4

(4)

其中，在m13的预测中，m8，m9，m17为插值点，权重为0.8，这三个点方向的真实像素与m13欧式距离较大，可信度较低，权重相对于m7，m12，m14，m18，m19这样的真实值较小。

原始图像中存在个别像素值为0或255的点被误判为噪声，但是相对于大量噪声点的影响，这些误判所造成的影响可以忽略不计。

当噪声像素在图像的四个顶点时，以周围的三个像素平均值做插值，当噪声像素在图像的图像边沿时，以周围的五个像素平均值做插值。

图像在经过加权修复后，视觉质量有了很大的提高。再使用常规的均值AMBTC算法压缩修复后的图像，得到最终的压缩文件。图5为经过处理的Lena图像，图5(a)为Lena的修复图像，图5(b)为Lena的AMBTC解压图像。

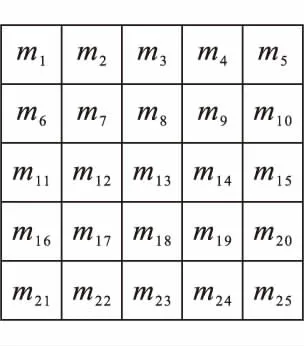
图4 5×5图像预测块

(a) (b)

本文算法的实验流程图如图6所示。

图6 算法流程图

3 实验结果

本文南加大SIPI数据集中的8幅512×512大小的灰度图像，分别为Lena，Peppers，Couple，Bridge，Elaine，Boat，Baboon和Airplane。噪声强度为0.1:0.1:0.4，当强度大于0.4时，图像基本信息已经无法正常显示，说明图像的信息源存在严重问题，图像信息已经没有太多的价值。实验平台为MATLAB 2013a，操作系统为64位windows 7，CPU为i5-5200u，主频为2.2Ghz，内存为8Gb。采用峰值信噪比(Power Signal-to-Noise Ratio，PSNR)和时间代价(Time Cost，TC)两种方法评价压缩效果。值得注意的是，PSNR越高，压缩算法的性能越好，TC越低，压缩算法的效率就越高。

当噪声为0.1时，Peppers的压缩效果如图7所示，图7(a)是原始图像，图7(b)是含噪声图像，图7(c)是修复图像，图7(d)是AMBTC压缩图像。噪声对图像有着严重的干扰，但是经过修复后，图像质量明显增强，和原始图像区别都不明显，再经过AMBTC压缩，图像质量有所下降，但是仍然在视觉的接受范围内。AMBTC图像相对于含噪声图像的视觉效果要好很多，事实上，图7(b)的PSNR为21.44dB，图7(c)的PSNR为40.61 dB，图7(d)的PSNR为32.81 dB。Airplane压缩效果如图8所示，其效果对比与图像Peppers类似，自适应修复可以很大程度地提升图像的质量，图8(b)的PSNR为22.77dB，图8(c)的PSNR为40.26 dB，图8(d)的PSNR为31.39dB。

(a) (b) (c) (d)

(a) (b) (c) (d)

当噪声强度为0.1，0.2，0.3和0.4时，8幅测试图的PSNR对比如表1所示，PSNR1为修复图像的PSNR值，PSNR2为AMBTC图像的PSNR值。PSNR1基本在30dB左右，说明即使噪声强度很大，修复后的图像视觉质量仍然可以接受。PSNR2在25dB以上，图像的细节部分丢失，但是基本信息仍然得到保留。说明在有噪声干扰的情况下，经过修复处理后，AMBTC算法可以很好地压缩图像。

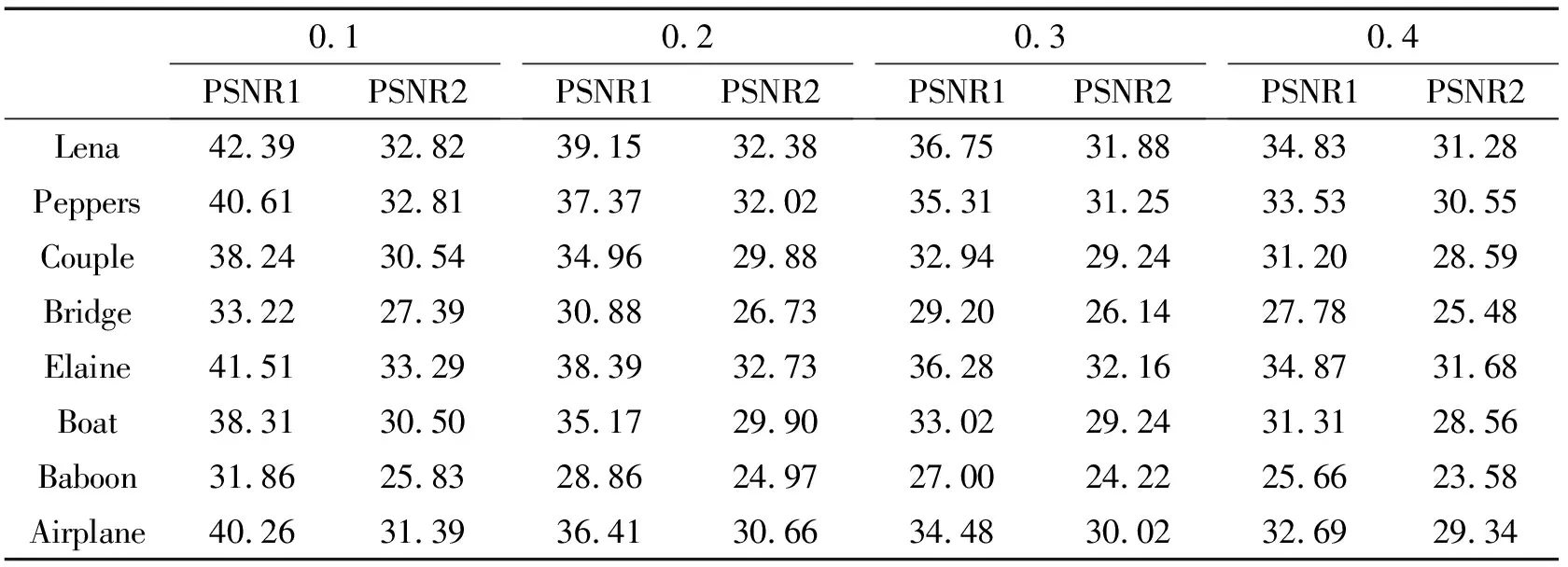
表1 测试图PSNR对比表

在压缩率为4的前提下，本文算法与AMBTC优化算法PSNR平均值比较如图9所示，本文算法在所有强度下的PSNR值优势明显，平均有10dB的提高。充分印证了对图像的内容的预处理的重要性，只有对图像内容认真筛选，才能保留属于原始图像的像素信息，这样AMBTC压缩才能有很好的显示效果。

为了进一步验证算法的有效性，8幅测试图的仿真时间对比如表2所示，计算开销的平均值对比如图10所示。在表2中，TC1为Hui等人[6]的方法，TC2为Zhang等人[10]的方法，TC3为本文的方法。Hui等人[6]采用了迭代寻优的策略，而Zhang等人[10]采用了定点预估确定搜索范围，这两种方法都可以降低运算的开销，但是都缺少滤除噪声的步骤，这样仍然存在很大的计算代价，同时无法得到最优的图像质量。本文算法避免了大量的迭代和搜索，省去了预估的环节，大大降低了计算量，这样计算复杂度进一步减小。

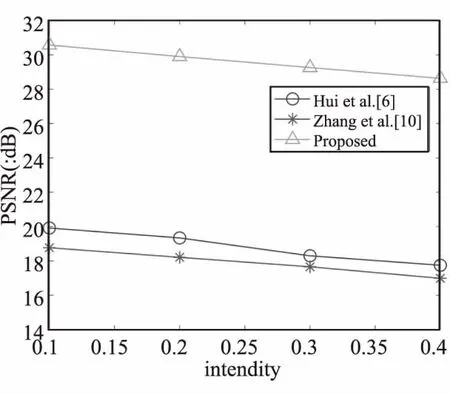
图9 PSNR对比图

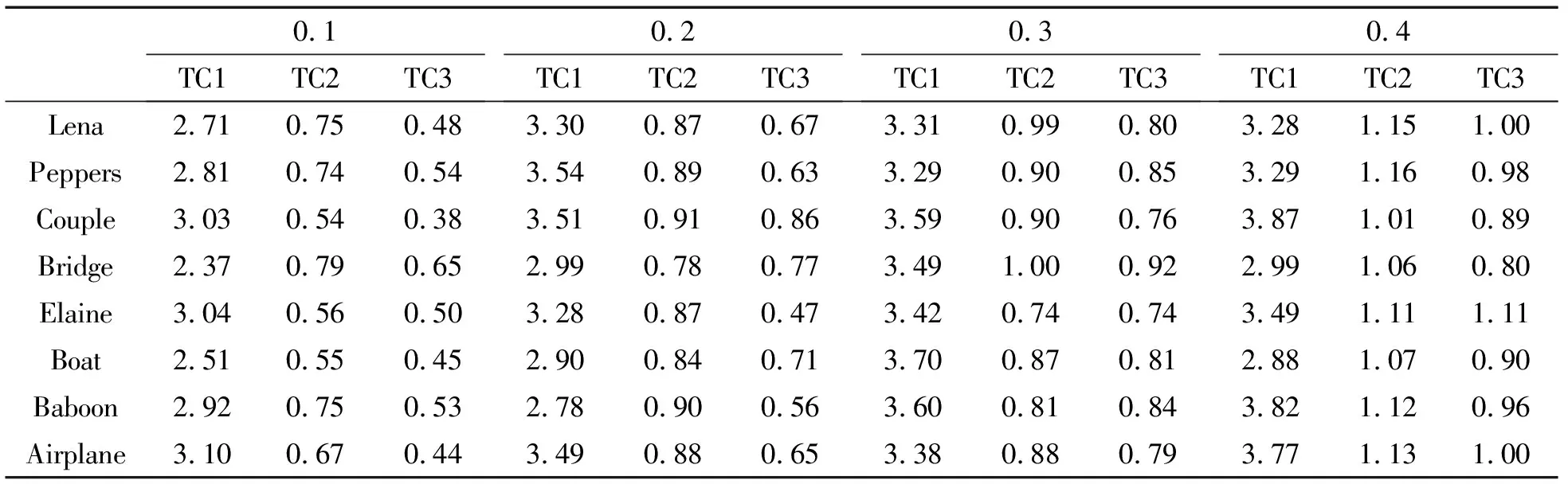
表2 测试图TC对比表

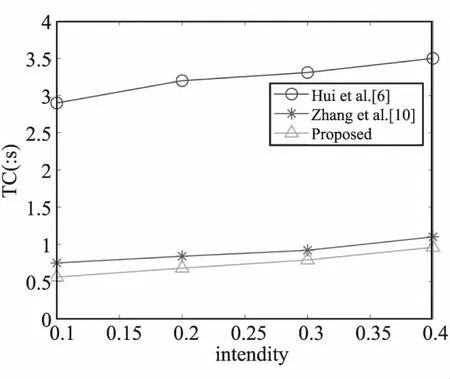
图10 TC对比图

为了验证本文算法在遥感图像中的泛化能力，本文采用南加大的38张图像进行算法比较，测试图像均为512×512的无损TIFF格式灰度图像。图10为4幅噪声强度为0.2的原始图像，图11为4幅最终恢复后的AMBTC图像，视觉上图像质量有了明显的提高。38幅图像的PSNR平均值对比如图12所示，TC平均值对比如图13所示，可以看到，该算法同样适用于遥感图像。

(a) (b) (c) (d)

(a) (b) (c) (d)

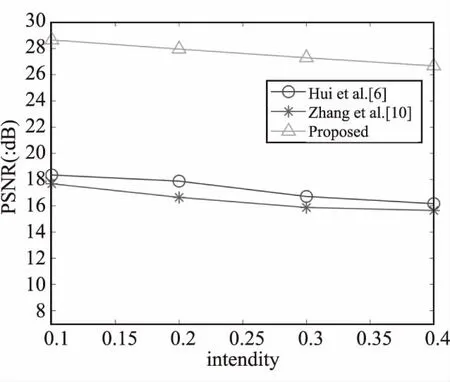
图13 遥感图像PSNR对比图

图14 遥感图像TC对比图

4 结论

本文提出了自适应预处理的AMBTC图像压缩算法，得到以下结论：

将图像中的椒盐噪声滤除，可以很大程度地提高数据内部的相关性，使用自适应预处理的方法，图像内容得到很好的修复。

与之前的文献相比，本文的AMBTC图像的PSNR平均提升在10dB，耗时小于1s。显示效果好，运算复杂度低，可以实时处理图像。

本文只考虑了椒盐噪声的情况，对于其他噪声还没有做进一步的研究。