基于微带谐振器耦合理论的可重发无芯片标签设计

黄能玉，郭佳庆，韦雪婷，马中华

(1.集美大学航海学院，福建 厦门 361021；2.集美大学信息工程学院，福建 厦门 361021)

0 引言

射频识别(radio frequency identification,RFID)是物联网中应用最广泛的一项技术，与条形码相比有许多优势，如自动识别，非视距读取，信息量大和安全性能高等，唯一的缺点就是价格比条形码高.该系统主要由读写器(也称为问询器)、标签(或应答器)和后台数据处理单元组成.这种系统有一些固定或移动的读写器，以及附着在包装、物品和设备等物体上成百上千的标签.读写器和问询信号在信号覆盖范围内进行通信，并收集相关数据信息.根据其工作原理，标签分为3类： 无源、半无源和有源[1].无源标签最简单，成本低，没有内部电源，使用读写器发送的电磁波为其内部电路供电，依靠反向散射将数据传送回读写器[2].在RFID系统中成本主要取决于标签，因此，为降低标签的成本和延长使用寿命，许多文献提出了无芯片标签[3-6].无芯片标签的成本远远低于硅芯片价格，与铜皮和条形码的接近.无芯片标签一般工作在较高频率，因为工作频率高趋肤深度越小，所需要的导体材料越少，可进一步降低标签成本.而且无芯片标签能够承受硅芯片不能承受的极限条件，如高温、潮湿等恶劣的工业环境.无芯片标签没有通信协议，读写器需要进行问询和信号处理等全部任务[7].

无芯片标签RFID系统的发展非常迅速，目前已经提出时域、频域和空间域3类无芯片标签，在时域中，分为射频(radio frenquency,RF)延迟线和声表面波(surface acoustic wave,SAW)无芯片标签.RF延迟线无芯片标签由于电磁 (electromagnetic,EM)波的速度很高，标签中延迟线的时间延迟非常短，很难计算延迟的持续时间，导致数据内容受到标签大小的限制，如果数据增加，尺寸将会急剧增加[3].SAW滤波器可增加编码能力，实现100多位的标签[4].但是SAW标签需要将声波转换成RF信号来发送和接收，换能器的成本甚至比硅芯片高，且不可印刷，成本非常昂贵.近年Herrojo提出一种高容量的时域工作的近场无芯片标签，通过标签中的谐振器链中预先确定的等距位置处的谐振单元存在与否调制输入信号，使得ID码存在于调制信号的包络中，这种标签可获得很高的数据密度.但是需要读写器和标签对准，而且读取速度要恒定[8-9].基于频域的无芯片标签数据被编码在反向散射信号的频谱中，可以在特定的频率上产生谐振[5].与时域的标签相比，此类标签编码容量巨大，可直接打印.但是这种无芯片标签读写器中发射机和接收机之间隔离度低的因素导致其动态范围和灵敏度差[10].在空间域方法中，标签的每个小部分都包含自己的数据，在标签表面上使用微小的谐振器来编码，利用EM图像传输[6,11-12].

基于频域的无芯片标签结构简单，容易读取加载的信息.这类标签又分基于重传类型的无芯片标签[13-15]和基于雷达散射截面(radar cross section,RCS)的反向散射无芯片标签[16-20].基于RCS理论的反向散射无芯片标签不需要单独的天线发送问询信号并接收反向散射信号.但是由于标签口径的关系，接收到的反向散射信号幅度很微弱.这种标签具有明显的优点： 尺寸小、易读性、不需要接收和发射天线.但是标签的性能明显依赖于单元的特定形状，添加单元可以扩展更多的位数但会明显引入耦合.校准来消除背景影响增加了读取器的复杂性，单元之间的影响增强，性能变得不可预测[18-20].可重发无芯片标签虽然额外增加了两面天线，但是两个正交极化天线会大大减少发射电磁波和接收电磁波之间的干扰，因此具有更稳定的性能.可通过在耦合结构中简单地添加更多的谐振器来增加标签容量，调整谐振器之间的距离可以减少谐振器之间的相互耦合，而且它传输的信号频谱功率高，系统的灵敏度高，读取距离远.基于此，设计基于微带耦合理论的可重发无芯片标签，谐振单元采用反向嵌套的C型微带.通过调节C型微带嵌套的深度调节谐振深度，实现幅度调制和频率位置调制的混合编码技术，提高了编码容量.背面采用接地板，这样隔离了标签贴附物体对标签性能的影响.由于采用可重发结构，标签的收发天线正交，减小了收发天线之间的相互干扰，提高了读写器灵敏度，可进一步增大读取距离.

1 工作原理

图1 可重发无芯片标签的工作原理Fig.1 Working principle of the retransmitted chipless tag

微带耦合可重发无芯片标签的工作原理如图1所示.为降低读写器和标签各自收发天线产生的自干扰，使它们相互正交极化.也为了提高读写器和标签的接收灵敏度和减小无线传输过程中的极化损失，读写器的发射接收天线和标签的接收发射天线极化特性一致.无芯片标签RFID读写器发射一个脉冲问询信号，此脉冲在频域是一频谱均匀的超宽带(ultra wideband,UWB)信号.标签天线接收到这一超信号后，让它经由微带传输线传输到标签的发射天线，传输过程中由于微带线旁边的C型微带反向嵌套谐振器的耦合作用，谐振器尺寸对应的谐振频率上形成频谱特征.当频谱特征出现时，对应逻辑状态“1”，频谱特征消失时，对应逻辑状态“0”.当不同尺寸的谐振器放置在传输线旁边，就会在UWB频谱上形成一系列的编码信号.基板选用罗杰斯微波板RO4350，相对介电常数3.66，损耗角正切0.004，基本厚度0.508 mm.

对图1所示的标签结构进行分析，可以用集总参数元件等效成多个不同谐振频率的一阶带阻滤波器.等效的集总参数电路如图2所示，滤波器之间用电感隔离，每个滤波器由LC串联的并联单元组成.标签的输入、输出分别与发射天线接收天线匹配.

图3为单个耦合谐振器的结构参数示意图，该结构能够产生明显的带阻响应.传输超宽带信号的微带线宽度为w1，谐振器和信号传输微带线之间的间距为d2，谐振器和微带传输线平行的底边宽度固定为d1，所有的谐振器耦合边宽度d1都相等，这样可以使所有谐振器的耦合系数近似相等，那么谐振器的谐振频率对应的频谱特征幅度相等.C型微带反向嵌套谐振器最外边的一边长度为L1，里面的C型微带一边的长度为L2，谐振器微带的宽度为w2.相邻谐振器之间的间距为d3.具体的参数值见表1.

图2 无芯片标签等效电路Fig.2 Equivalent circuits of chipless tag

图3 单个耦合谐振器的结构参数Fig.3 Structural parameters of a single coupled resonator

表1 结构参数值

图4 单个耦合谐振器的频谱曲线Fig.4 Spectrum curve of a single coupled resonator

用高频结构仿真器(high-frequency structure simulator,HFSS)软件对单个C型反向嵌套微带谐振器耦合传输线进行模拟，得到如图4所示的具有频谱特征的谐振曲线.C型反向嵌套微带谐振器形成一个带阻谐振特性，当L1=6 mm的单个谐振器基波频率为6.15 GHz，在9.63 GHz频率处有一个干扰频率.对于基波，频谱特征的凹陷深度达到了-14 dB，占用的频谱宽度很窄，品质因数Q达到52，因此这种谐振器进行频率调制编码时频谱利用率非常高.改变C型反向嵌套微带谐振器的边长，就会在频谱上形成各种谐振频率对应的具有凹陷结构的频谱特征.

2 仿真设计

设计并制作了8 b编码分别为ID11111111，ID10101010和ID01010101的标签，如图5所示.图5(a)中最大的谐振器具有最低的谐振频率，最小的谐振器具有最高的谐振频率.去除标签上的C型微带反向嵌套谐振器，相应的频谱特征就会消失.但是每个谐振器会对相邻谐振器的谐振频率产生影响，当去除某一个谐振器时，相邻谐振器的谐振频率会发生偏移.为了减小这种对谐振频率的影响，把逻辑状态为“0”的谐振器短路，而不是去掉.

用HFSS软件对图5所示的标签结构进行模拟仿真，得到图6所示的3种典型编码标签ID11111111，ID10101010和ID01010101的谐振曲线.把ID11111111标签作为参考标签，其8个谐振器对应的谐振频率分别为5.43、5.60、5.77、5.89、6.08、6.28、6.42和6.66 GHz，频谱特征的凹陷深度处于-8.4到-11.4 dB之间，每个谐振器对应的频谱宽度固定，幅度一致性较好.图6把对比标签ID10101010，ID01010101与参考标签ID11111111的谐振曲线进行对比，把逻辑状态为“0”的谐振器用微带线短路，相邻逻辑状态为“1”的频谱特征的中心频率并没有发生较大偏移.但是参考标签对应的谐振频率为5.77 GHz频点时，对比标签ID10101010对应的谐振频点偏离了20 MHz，其余频点和参考标签对应的频点基本一致，频谱特征的凹陷幅度也和参考标签基本吻合；当参考标签对应的谐振频率为6.28 GHz频点时，对比标签ID01010101偏离了50 MHz，其余频点和参考标签对应的频点相同，但是单个谐振器的带宽为118 MHz.从上面的频谱特性可以看出，每个谐振器的频谱宽度基本不变，约为120 MHz，再增加一个80 MHz的保护频带，那么每一个谐振器占据200 MHz的带宽.也就是说此类无芯片标签单个谐振频谱特征的频率分辨率是200 MHz，为了防止检测错误，谐振器的带宽必须小于这个值.

从图4得知，对于频率为6.15 GHz的基波，在9.63 GHz处还有一个谐波，它的出现会干扰处于9.63 GHz处对应的谐振器的频谱特性，结果会产生误码.所以，可用的编码频段只能是处于6.15到9.63 GHz这一段，总共可以得到17个频率位置编码.为增大编码容量，可以减小第一位编码的谐振器尺寸，让其谐振频率提高，这样可用带宽会增加，而本文提出的谐振器无论尺寸怎么变化，谐振特征的频谱宽度基本保持不变，增加了编码容量，但是最后会受到微带加工精度的限制.

图5 无芯片标签结构Fig.5 Chipless tag structure

图6 3种典型编码标签的谐振曲线Fig.6 Resonance curves of three typical coding tags

图7是参考标签的仿真和测试频谱特征曲线，测试和仿真的谐振频率基本一致，第6谐振频点和第8谐振频点偏移稍大，分别为90和130 MHz.图7曲线中仿真的频谱幅度比实测的频谱幅度要大，这是因为在测试过程中连接标签和UWB天线的转接头有一定的插损，UWB天线的匹配性能不是处于最优状态也会带来一定的损耗，因此实测和仿真幅度大约相差6～7 dB.图8是实测图5中制作的3种典型编码标签频谱特征对比曲线.实测曲线显示了两种编码的正确频谱特征，当谐振器短路时，对应的频谱特征消失，编码状态由逻辑“1”变为逻辑“0”状态.所有实测的标签编码逻辑状态为“1”的频谱特征对应的谐振频率基本一致，不会产生大的偏移.

图7 参考标签仿真和实测的频谱曲线Fig.7 Simulated and measured spectrum curves for reference tag

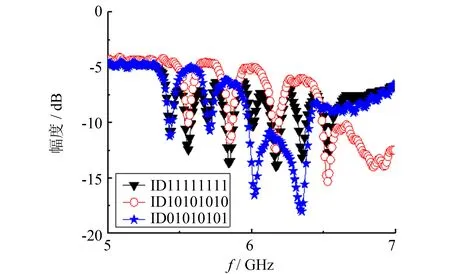
图8 实测图5 3种典型编码标签的频谱曲线Fig.8 Measured spectrum curves of three typical coding tags in Figure 5

3 性能分析

因为采用了本文提出的谐振器结构，各个谐振器对应的谐振频谱没有扩展，占用带宽基本相同.但是最高位的谐振器受到最低位谐振器的高次谐波限制，如图9所示，最低位谐振器的谐振频率是5.43 GHz，它产生的谐波是7.69 GHz，那么最高位谐振器对应的谐振频率就不能超过7.69 GHz.为增加可编码的频带宽度，可提高最低位谐振器的谐振频率，即减小谐振器的尺寸，因为每个谐振器所对应的带宽是固定的，这样可以增加编码容量.最后编码容量的增加受谐振器尺寸的加工精度等因素的约束.

为减小标签面积，需要减小谐振单元之间的距离，但是单元之间的互耦会增强.本文采用的是逻辑状态为“0”时将谐振单元短路，而不是去掉，所以其互耦不会发生变化，因此不会影响谐振频率点.图10是当谐振器间距d3改变时，标签的频谱特征和谐振频率的变化.可以看到，d3增大时，频谱特征的幅度没有改变，而谐振频率略有增加，但还是能够清晰地分辨出每个谐振器对应的谐振频谱特征.

图9 标签ID11111111的频谱曲线Fig.9 Spectrum characteristics of tag ID11111111

图11为结构参数t改变时的谐振曲线.当t变化时，谐振点对应的幅度基本不变，大概在-13 dB左右上下波动；但是谐振频率会随t增大，向高频端移动.图12为微带宽度w2改变时的谐振曲线，从图中看到，随着w2变宽，谐振频率向低频端移动，而且带宽也随着拓宽，谐振凹陷的深度加深.

图11 参数t改变的谐振曲线Fig.11 Resonance curves of different parameters t

图12 微带宽度w2改变的谐振曲线Fig.12 Resonance curves of different microstrip widths w2

4 结语

提出一种具有固定带宽的C型微带反向嵌套的谐振器构成的可重发无芯片RFID标签模型.分析了单个谐振器的频谱特征，以便更好地应用到无芯片标签的设计中.通过软件建模仿真和做板实测来验证8 b C型微带反向嵌套谐振器耦合微带传输线的标签，比较结果证实了仿真和实测的一致性和正确性.