Allee效应对阶段结构单种群模型的动力学行为影响

黄小燕,陈凤德

(福州大学数学与计算机科学学院,福建 福州 350108)

0 引言

在自然界中有许多物种都需要经历不同的生命阶段,从幼年到成年,从不成熟到成熟等.物种在不同阶段有不同的特征,为了更贴切实际情况,学者们提出了阶段结构单种群模型.文献[1]的研究结果表明阶段结构单种群模型当幼年种群的出生率足够小时,种群最终会绝灭,反之种群会长久生存.Allee效应是当前研究的热点，很多学者在各种生物模型上进一步考虑Allee效应的影响[2-12].文献[2]提出了出生率具有Allee效应和非线性转化率的阶段结构蚊子模型,探讨了正平衡点存在性以及局部稳定性，但没有研究平衡点的全局稳定性及其分支现象.由于文献[2]没有考虑到成年种群的密度制约项,导致系统的平衡点存在条件和局部稳定性探讨相对简单.有鉴于此，本研究将在单种群阶段结构模型的基础上,在出生率中考虑了Allee效应,研究其动力学行为.

1 模型

本研究在文献[1]模型的基础上进一步考虑幼年种群出生率具有Allee效应的阶段结构单种群模型:

(1)

这一模型与文献[2]中模型相比较,表面上未考虑幼年种群的非线性转化率等,但进一步考虑了成年种群的密度制约作用,这使得系统会产生与文献[2]中不一样的新的动力学行为.

2 平衡点的存在性

无论系统(1)的参数如何变化,其总是存在唯一一个边界平衡点E0(0,0).接下来,讨论系统(1)正平衡点的存在情况.

定理1Ⅰ) 当α<α2时,系统(1)没有正平衡点;

Ⅱ)当α=α2时,系统(1)只有唯一一个正平衡点E*(x*，y*);

(2)

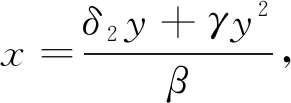
2) 当Δ=0时,得到α=α1或α=α2. 若α=α1,系统(1)不存在正平衡点; 若α=α2,系统(1)存在唯一一个正平衡点E*(x*,y*),其中x*,y*见方程(2).

3 平衡点的稳定性

系统(1)在E0(0,0)处的雅可比矩阵为:

所以其有两个特征值分别为λ1=-(β+δ1)<0,λ2=-δ2<0.则E0(0,0)是局部渐近稳定的.

证明 构造Lyapnov函数V(x,y)=(σγ+δ2)x+αy.显然,V(x,y)是定义在x>0,y>0上的连续正定函数,V(x,y)沿着系统(1)的导数为:

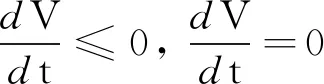
正平衡点的雅可比矩阵的迹trJ=-(β+δ1+δ2+2γy)<0.正平衡点的雅可比矩阵的行列式为

首先,本研究先通过变换(X,Y)=(x-x*,y-y*)将E*平移到原点处,并在原点作幂级数展开,系统(1)变为：

(3)

其中:P1(X,Y)是包含项XiYj(i+j≥6)的幂级数.

然后再做变换

则系统(3)变为

(4)

其中:P2(u,v),P3(u,v)都是包含项uivj(i+j≥6)的幂级数.

最后令dτ=(a1+b2)dt,系统(4)变成

4 分支

定理3系统参数满足临界条件

系统(1)存在一个鞍结分支,此时

且α作为分支参数.

证明 系统(1)在平衡点E*处雅可比矩阵的行列式为0,所以J(E*,αSN)有一个零特征值,不妨记为λ.令V和W分别为矩阵J(E*,αSN)和J(E*,αSN)T的属于特征值λ的特征向量,则

WTFα(E*;αSN)≠0,WT[D2F(E*;αSN)(V,V)]≠0

由文献[4]中的Sotomayor’s定理知系统(1)在E*处有一个鞍结分支.证毕.

5 数值模拟

2) 设置参数α=0.4,β=0.2,δ1=0.3,δ2=0.1,γ=0.2.① 取σ=0.5,此时E0(0,0)全局稳定,见图3,红黄蓝绿分别表示初值为(0.7,0.3),(0.9,1.2),(1.7,2.1),(2.8,1).② 取初值(0.7,0.3),红黄蓝绿分别表示σ=0.5,0.9,1.2,2.5,E0(0,0)全局稳定,见图4,相同初值,σ越大则解趋于(0,0)的时间越短.

图3 E0全局稳定Fig.3 Global stability of E0

图4 Allee效应对E0趋于平衡的速度影响Fig.4 The effect of the Allee effect on the speed at which E0 tends to balance

6 结论