基于最小均方自适应算法的光纤陀螺信号实时滤波方法

杜建邦，何金阳,2，卓 超

（1. 北京航天自动控制研究所，北京 100854；2. 宇航智能控制技术国家级重点实验室，北京 100854）

高速、高机动飞行器具有突出的快时变、强耦合、非线性和不确定性等特点，这给其上安装的旋转调制式惯导系统的旋转轴稳定控制带来了严峻的挑战。光纤陀螺具有工作原理先进、结构简单、无活动部件及抗冲击能力强等优点，是高精度稳定控制系统的理想角运动敏感元件。但光纤陀螺相比于传统的机电陀螺，其输出信号易受光路、电路随机噪声的干扰，产生的角速率漂移会严重影响系统控制精度[1]。为了实现系统的高精度稳定控制，需要对控制系统中的反馈信号—光纤陀螺的输出进行降噪滤波处理[2,3]。

目前，工程中广泛采用低通滤波器对陀螺信号进行滤波，滤波器的截止频率、通带等参数主要根据工程要求及经验确定。由于传统低通滤波器采用固定的滤波器系数，难以满足光纤陀螺非平稳随机信号条件下的精确滤波。自适应滤波器则能够实时地调节当前时刻的滤波系数以适应随机信号的时变统计特性，可以实现一定意义下的最优滤波，因此更加适用于光纤陀螺输出信号的滤波处理。在自适应滤波器设计中，最小均方（Least Mean Square，LMS）算法使用随机梯度下降的方法实现代价函数的最小化，具有计算复杂度低、无需统计数据的先验知识和均值无偏地收敛到维纳解等优点，成为自适应算法中应用最广泛的一种[4]。为解决各类实际问题，相关学者提出了诸多变步长LMS 算法及变换域的LMS 算法[5,6]。文献[7]提出了级联的LMS 自适应的降噪方法。该算法采用了变步长和不同滤波器初始权值的自适应算法，通过仿真结果表明，该方法在滤波精度和实时性等综合性能方面具有一定的优越性。文献[8]针对光纤陀螺输出噪声的问题，提出了一种基于最小均方法与二代小波变换相结合的降噪方法，该方法提高了捷联惯性导航初始对准姿态精度。文献[9]提出了基于归一化LMS 算法的前向线性预测滤波器的降噪方法，该方法显著降低了角随机游走噪声，实现了单个光纤陀螺对地球自转速度的精确测量。然而，目前大多LMS 自适应滤波器的相关研究均以静态滤波精度作为主要设计指标，没有考虑时延特性，适用于陀螺寻北和初始对准等动态性要求较低的场景，无法满足高动态条件下旋转调制式惯导系统旋转轴稳定控制系统的滤波需求。

本文针对旋转惯导稳定控制对滤波器高频消噪与时延等要求，在综合考虑了期望信号、滤波器阶数和信号采样率等影响因素后，设计了一种优化的LMS自适应滤波器。该滤波器兼顾了动静态性能要求，适用于大动态、高精度稳定控制系统，具有结构简单、工程实现方便等优点。

1 LMS 自适应滤波器原理

最小均方（LMS）自适应滤波器的结构如图1(a)所示，包括横向滤波器与LMS 算法两部分[9]。横向滤波器（图1(b)所示）本质为FIR 结构的维纳滤波器，其输出信号是输入信号u(n- 1 ),u(n- 2)…u(n-M)的线性组合。LMS 算法根据期望信号d与的误差调整横向滤波器的权系数向量，从而适应随机信号的时变统计特性。

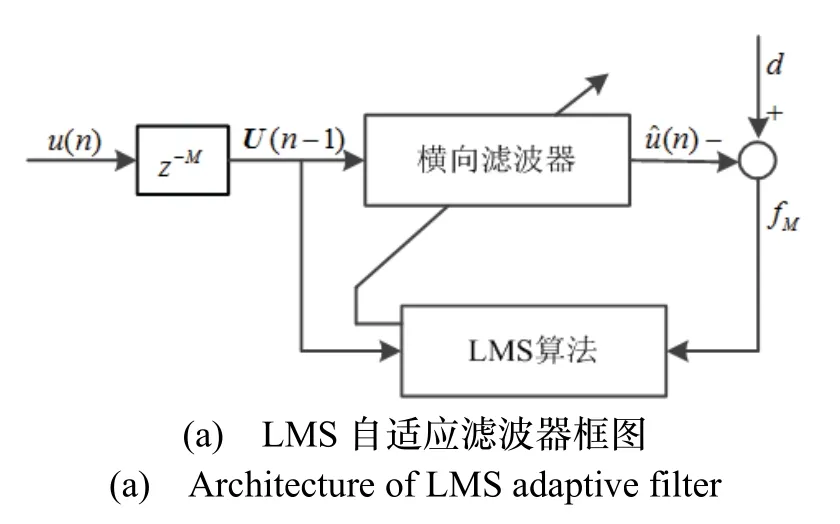
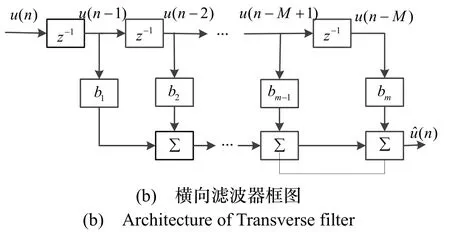
图1 LMS 自适应滤波器原理Fig.1 Principle of LMS adaptive filter

LMS 自适应滤波器的输出是当前采样值u(n)的估计值，的计算公式为：

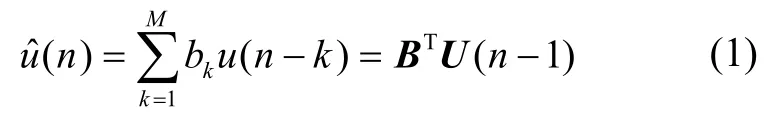
式(1)中，BT= ［b1,b2,b3,…bm］是横向滤波器系数组成的向量；U(n- 1) = ［u(n- 1 ),u(n- 2),u(n- 3),…u(n-M)］T是滤波器输入向量。

定义估计误差fM为：

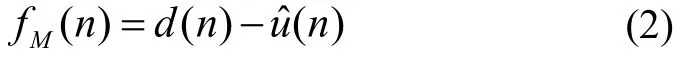
将估计误差的最小均方误差作为最优的统计准则，定义代价函数J为：

式(3)中，E表示估计误差平方的数学期望；J随时间的变化表征了滤波器的收敛速度与收敛精度。

需要解决的问题是如何选择滤波器的权值使得的均方误差最小，或者说当J最小时滤波器的权值最优。最优权向量Bopt可表示为：

式(4)中，R为输入信号的自相关矩阵，rxd为输入信号与期望响应的互相关矢量。在实际系统中，特别是环境未知时，一般很难获得滤波器输入信号与期望响应的统计特性（R和rxd），因此，采用对非平稳环境具有学习能力的自适应LMS 算法对权系数向量进行实时估计，逐步逼近最优权值。根据LMS 算法，通过以下公式反复迭代，权值逐渐逼近其最优解：

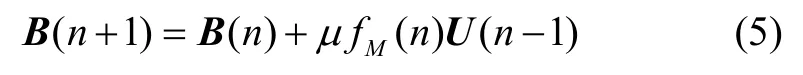
式(5)中，μ是权值更新步长，μ的收敛范围为：

λmax为输入信号自相关矩阵R的最大特征值。

相关学者在传统LMS 算法上提出了许多优化算法，其中归一化LMS 算法采用了可变更新步长，具有收敛速度更快、滤波器时延小的优点，因此适用于稳定控制系统的滤波需求，其权值迭代公式为：

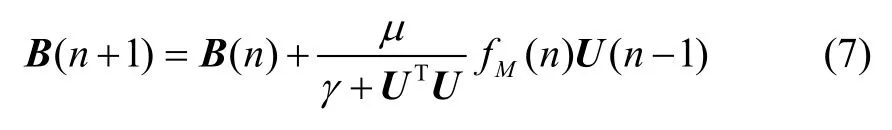
式(7)中，γ是一个很小的常数以保证分母不为零，μ的收敛范围为：

2 LMS 自适应滤波器优化设计

针对高精度稳定控制系统对滤波器的性能要求，为了实现LMS 自适应滤波器的优化设计，需综合考虑各种因素对滤波器性能的影响。根据第一节，归一化LMS 自适应滤波器的性能主要取决于权值更新步长μ、未知环境下的期望信号d和滤波器阶数M三个参数。本节结合实际控制系统对滤波器的性能要求以及光纤陀螺实验数据，分析相关参数对滤波性能的影响并进行滤波器的优化设计。

2.1 权值更新步长μ

由式(7)可得，权值更新步长μ决定了权值大小。为了进一步分析μ对滤波性能的影响，以光纤陀螺静态数据作为输入信号，其他滤波器参数一定，对比μ=0.001，μ=0.1 和μ=1（0＜μ≤1）三种不同步长滤波器的滤波效果。图2 展示了滤波结果的均方误差J随时间变化的曲线。

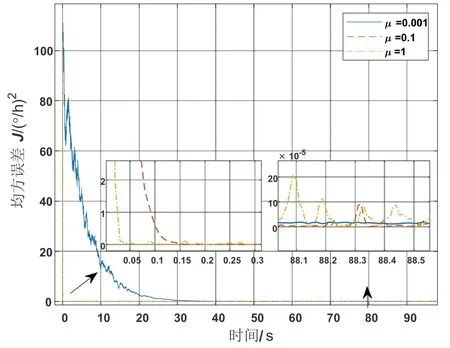
图2 采用不同步长滤波的均方误差曲线Fig.2 MSE curves with different update step length

由图2 可得，步长μ影响着收敛速度和滤波精度。随着μ的增大，收敛速度变快，但收敛后在最优解附近波动幅值变大，稳态精度相应降低；μ过小，虽可保证滤波精度，但收敛时间大大增加，无法保证系统实时性。因此需要根据收敛速度和滤波精度折中选取μ。旋转惯导稳定控制系统要求滤波器在动态突变环境下能够快速收敛，相比于收敛后较低量级的波动幅值，μ的选取应侧重考虑收敛速度。

2.2 期望信号d

目前已发表的相关文献中，自适应滤波器的期望信号通常采用当前时刻的信号采样值，即d(n) =u(n)，但是当前时刻采样值u(n)包含了较大的噪声，导致期望信号的波动，影响了滤波精度。为了减小期望信号这种不稳定性的影响，对期望信号的选取进行优化，选取过去时刻采样值的平均值作为期望信号，即

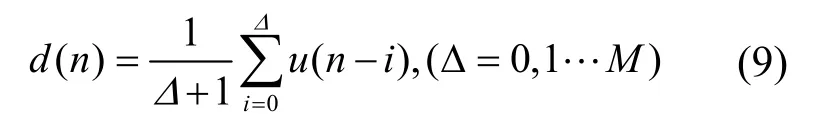
式(9)中Δ表示选取的采样点数。Δ选取的原则为既要有效地减小当前时刻采样值的噪声，也不能对当前时刻采样值的真值造成影响以及产生太大的时延。随着Δ的增大，当前时刻信号的噪声强度随之降低，但增加了滤波器输出信号的时延。另外，随着Δ的增大，与当前时刻信号的相关性逐渐降低，也会影响当前时刻期望信号真值的确定。

通过以上分析，利用光纤陀螺静态数据作为输入信号，其他滤波器参数一定，选取Δ=0，Δ=5 和Δ=M（M为滤波器阶数，此处选定M=10）三种典型的期望值进行滤波器性能的比对分析。不同期望信号滤波后的结果及其均值、标准差统计如图3 和表1 所示。

不同期望信号滤波后的结果及其均值、标准差统计如图3 和表1 所示。

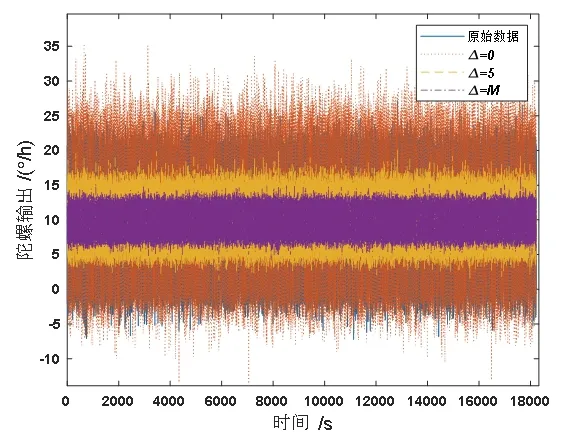
图3 采用不同期望信号的滤波结果Fig.3 Filtering results with different expected signal

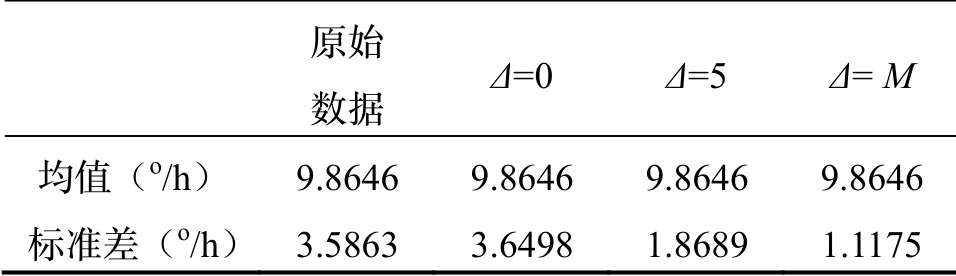
表1 不同期望信号下滤波后信号滤波均值与标准差统计Tab.1 Mean value and standard deviation of filtering results with different expected signal

由图3 和表1 可得，当Δ由0 增大至M时，滤波器降噪能力明显提高。

进一步验证Δ增大对动态响应的影响，令滤波器跟踪正弦信号，滤波后产生的相位延迟可用式(10)估算：

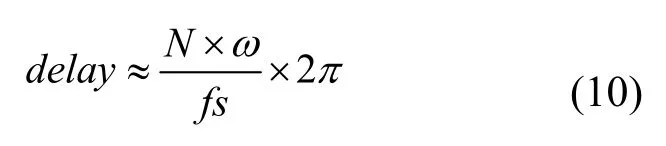
其中，N为滤波器输出信号滞后的采样点个数，ω为信号的角频率，fs为信号采样频率。对于角频率为20 Hz 的正弦信号滤波后相位延迟如表2 所示。

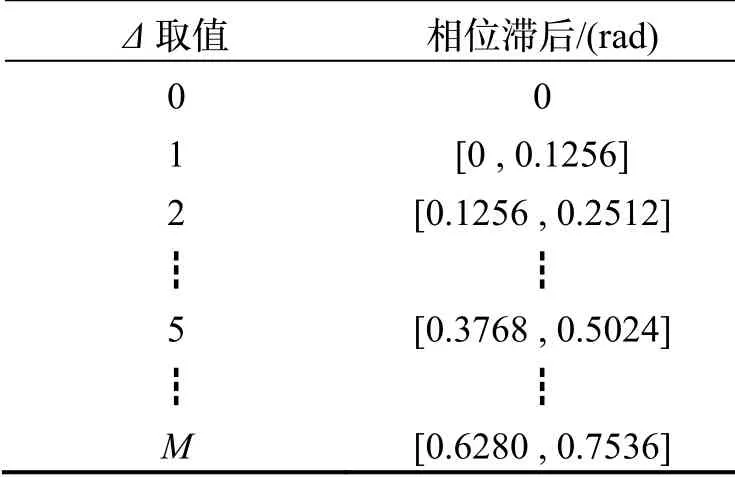
表2 不同Δ 的相位延迟Tab.2 Phase delay with different Δ

由表2 可知，随着Δ增大，期望信号包含了更多过去时刻的采样信息，滤波器的动态响应相应降低。因此，Δ影响滤波精度和时延，需综合考虑信号的噪声特性、信号的相关性以及控制带宽的要求选取Δ值。

2.3 滤波器阶数M

滤波器阶数M影响着滤波器收敛速度和滤波精度。为了探究M对滤波性能的影响，利用光纤陀螺静态数据作为输入信号，其他滤波器参数一定，对比M=10，M=50 和M=100 三种阶数滤波器的滤波效果。滤波结果信号的均值、标准差统计如表3 所示，滤波结果的均方误差J随时间变化的曲线如图4 所示。

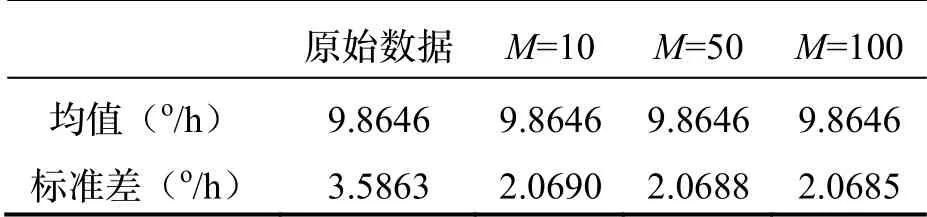
表3 采用不同阶数滤波后信号的均值与标准差统计Tab.3 Mean value and standard deviation of filtering results with different filter orders

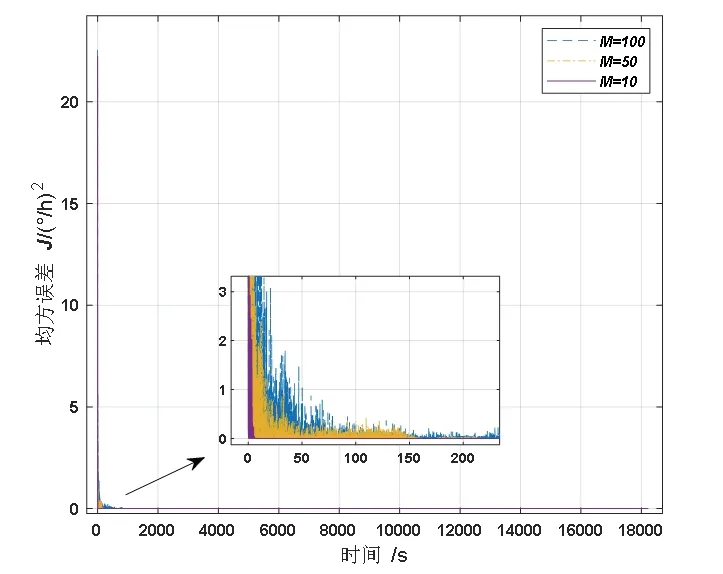
图4 采用不同阶数滤波的均方误差曲线Fig.4 MSE curves with different filter orders

由图4 和表3 可得，滤波器阶数M增大，滤波精度有所提高，但滤波器收敛速度明显降低。针对高精度稳定控制系统对滤波器短时延的需求，滤波器阶数M的选取也必须优先考虑收敛速度。

2.4 采样率fs 的影响

目前的相关文献大多针对某一特定采样率进行分析，而采样率对滤波器的设计非常重要。高频采样得到的滤波器输入信号通常噪声较强，通过对高频采样数据进行适当地平滑处理，可以有效降低高频噪声，但会引起滤波器时延的增加。在设计滤波器时要综合考虑采样频率的影响，合理选取滤波器参数。

3 实验验证与分析

根据2.1～2.4 节分析可得，LMS 自适应滤波器的滤波精度主要取决于期望信号d表达式中的Δ值，收敛速度主要取决于权值更新步长μ和滤波器阶数M。在综合考虑滤波精度和收敛速度的需求、光纤陀螺输出信号特性与采样率后，优化选取的LMS 自适应滤波器参数为：

为了验证优化后LMS 自适应滤波器的滤波效果，设计了静态与动态两类实验并与传统低通滤波器进行性能对比。采用具有线性相位的10 阶FIR 滤波器作为对比，采样率为1000 Hz，滤波器系数见表4，FIR 滤波器截止频率为250 Hz，通带衰减小于10-2dB，遵循最小相角设计，20 Hz 处的相角为-0.1988 rad。

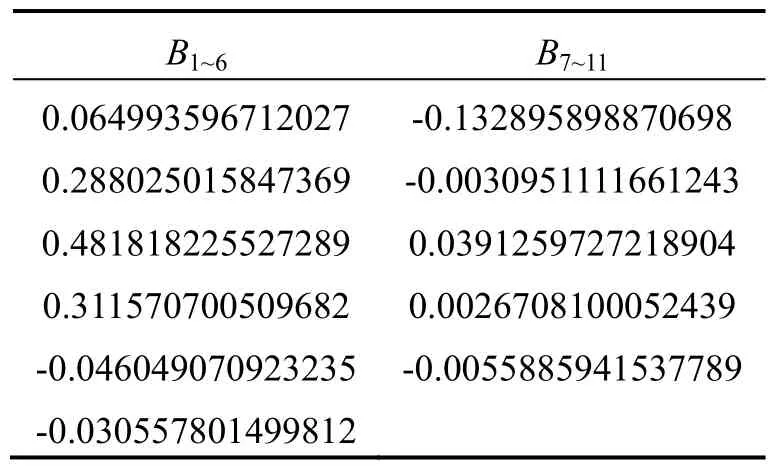
表4 FIR 滤波器系数Tab.4 Coefficients of FIR filter

3.1 静态实验

将光纤陀螺静置于转台，采集陀螺输出数据并利用LMS 与FIR 滤波器进行实时滤波处理，图5 展示了两种滤波器的滤波效果，表5 统计了滤波后信号的均值与标准差。

由表5 和图5 可见，优化的LMS 自适应滤波器有效地降低了高频噪声，高频噪声降低了约42.35%，降噪能力比低通FIR 滤波器提高了约9.16%。

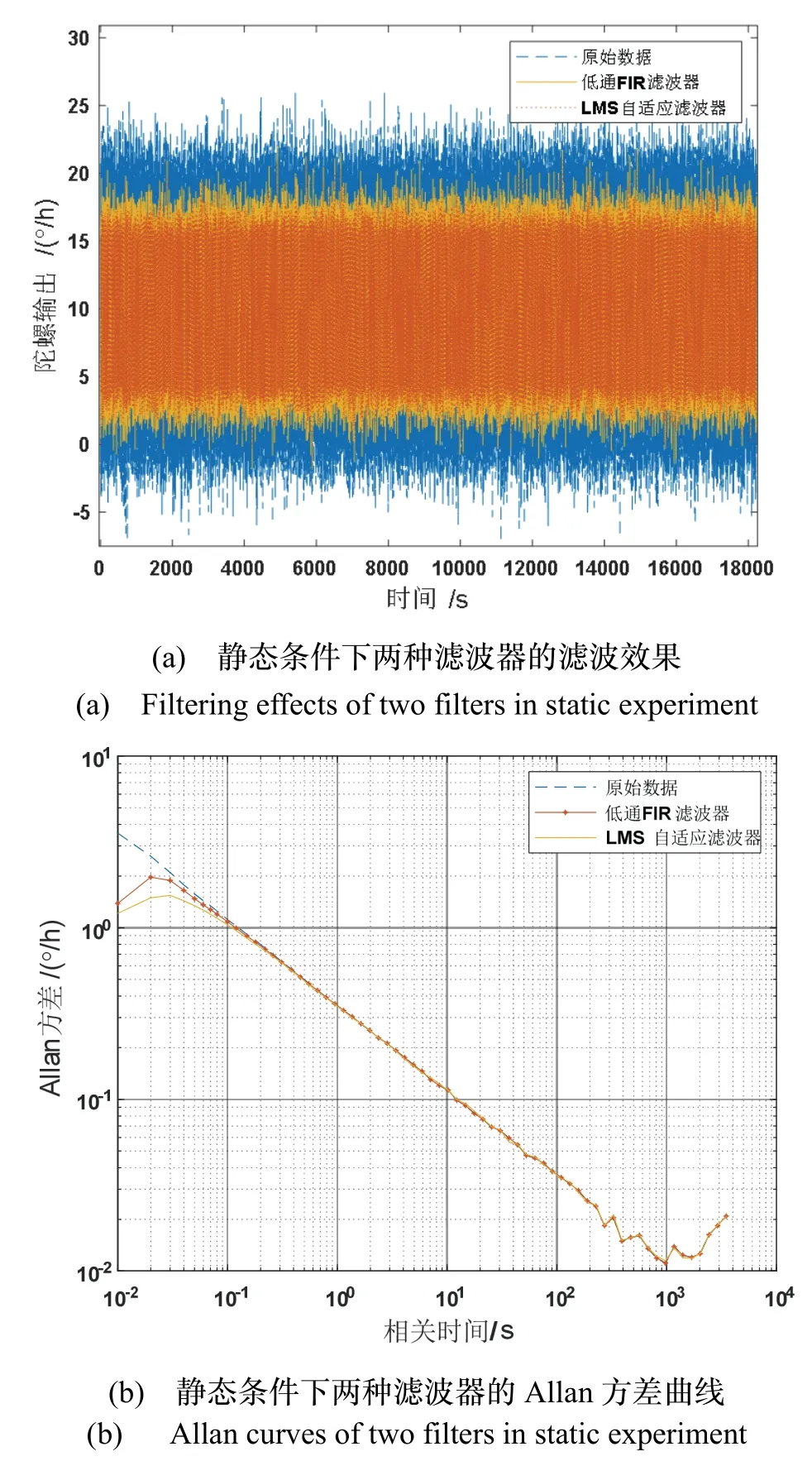
图5 静态条件下LMS 和FIR 滤波器的滤波结果对比Fig.5 Comparison of filtering results of LMS and FIR filters in static experiment

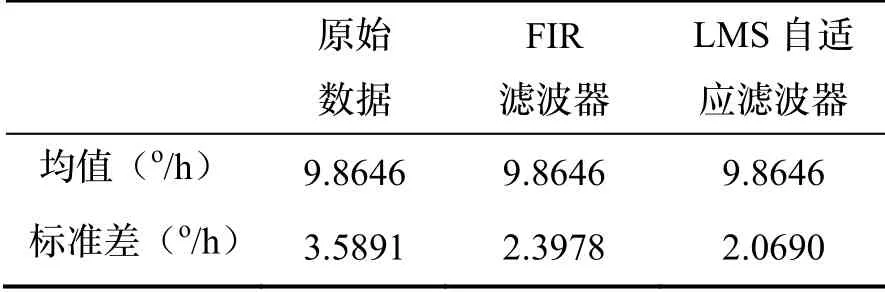
表5 经两种滤波器滤波后信号的均值与标准差统计Tab.5 Mean value and standard deviation of the output signal processed by two filters

3.2 动态实验

将光纤陀螺置于转台进行摇摆试验，受转台性能所限，只控制转台做1 Hz 摇摆运动，采集陀螺输出数据并做实时滤波处理，两种滤波器的动态跟踪情况如图6 所示。

由图6 可知，在1 Hz 摇摆运动条件下，优化的LMS 自适应滤波器比FIR 滤波器的相位延迟小0.108 °，提高了约18.96%。

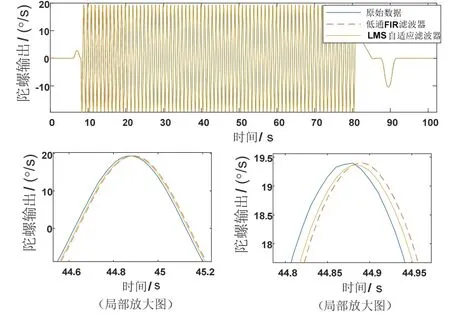
图6 摇摆状态下LMS 和FIR 滤波器的滤波效果对比Fig.6 Filtering effects of LMS and FIR filters in swaying experiment

3.2 动态突变实验

仿真产生一组动态突变信号，选取不连续角频率的正弦运动，角频率由1 Hz→20 Hz→40 Hz→100 Hz突变，两种滤波器对动态突变信号的跟踪情况如图7(a)所示，LMS 自适应滤波器收敛过程的均方误差曲线如图7(b)所示。由图7 可得，LMS 自适应滤波器可快速收敛，能够较好地跟踪动态突变信号，且相位延迟小于低通FIR 滤波器。

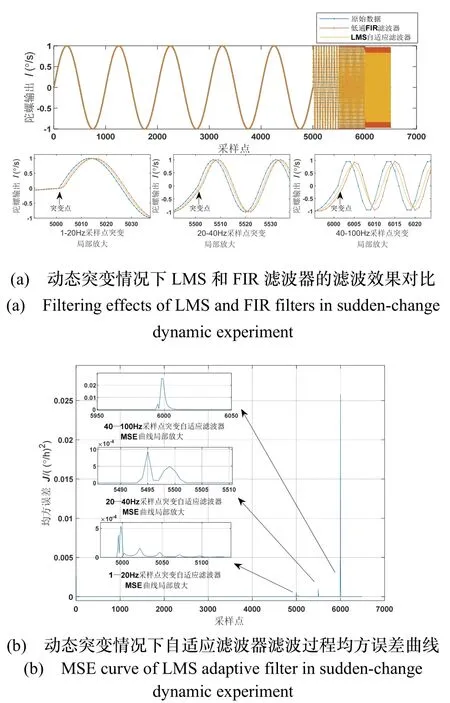
图7 动态突变情况下LMS 和FIR 滤波器的滤波结果对比Fig.7 Comparison of filtering results of LMS and FIR filters in sudden-change dynamic experiment

4 结 论

本文提出了一种适用于旋转调制式惯导的旋转轴稳定控制的优化LMS 自适应滤波方法。通过对滤波器主要参数进行优化选取，滤波性能可以较好地满足高频消噪与时延的要求。相比于工程中常用的传统FIR 滤波器，其降噪能力提高了约9.16%，相位延迟降低了约18.96%。该滤波器结构简单、易于实现，具有工程应用参考价值。后续将根据飞行试验结果，进一步完善算法设计。