一种地面用静电悬浮加速度计的误差分析及仿真

贺晓霞，李娇娇，李海霞，韩丰田，刘云峰

(清华大学精密仪器系导航技术工程中心，北京 100084)

静电悬浮加速度计是一种利用静电力实现多自由度支承、进行加速度检测的惯性仪表。目前静电加速度计广泛应用于低过载环境，常用于星载微重力测量[2]、空间基础物理实验等领域，如等效实验的验证[2-4]，引力波的探测[5]等。寻求小型化、低成本的面向海空重力测量的高精度静电悬浮加速度计方案，是提升我国惯性导航系统、重力测量系统整体精度的重要途径。法国 ONERA 研发第一代加速度计CACTUS，敏感质量块采用铂铑合金制成球状体，由于球的几何形状以及电极缺陷导致该加速度计的精度并不高。后续陆续研制ASTRE、STAR、Super-Star和GRADIO 系列加速度计，均采用长方体结构敏感质量块，实现了六自由度加速度的测量但降低了量程[6]。美国研制的MESA 加速度计进行了敏感探头从圆筒型到立方体的改进，主要面向空间微加速度测量[7]；兰州物理所从2000年左右开始静电加速度计相关研究，主要用于重力测量卫星的无拖曳控制、重力梯度卫星[8]；华中科技大学已研制了空间加速度计样机，并开展了空间搭载实验及基础物理实验[9]。国内其它研究单位也对空间静电加速度计开展过一些理论研究和设计分析，比如清华大学[10]，中国空间技术研究院[11]，南昌航空大学[12]等。

本文提出了一种适合地面应用环境的高精度三轴静电加速度计方案，该加速度计方案中，中心固定有一薄法兰盘的空心薄壁圆筒敏感质量，圆筒内外侧与法兰盘两侧布置检测和加力电极。本文对此敏感质量存在加工中的典型误差时如圆盘上下表面平行度误差、圆盘与圆柱垂直度误差进行了位移测量误差、力耦合误差的分析，为设计和后续建模提供依据。本文基于MATLAB/Simulink，建立了一套三轴静电悬浮加速度计控制系统仿真模型，设计了加速度计的控制参数，并比较分别采用盘面电极与柱面电极作为敏感质量位移与姿态检测的测量电极时，典型误差源对加速度计标度因数的影响程度。

1 静电悬浮加速度计的结构

静电悬浮加速度计主要包括五个部分：敏感质量与电极板结构、电容检测电路、滤波解调电路、数字控制电路以及高压放大加力电路。加速度计是一种闭环力平衡型加速度计，其一个轴的工作原理如图1 所示。

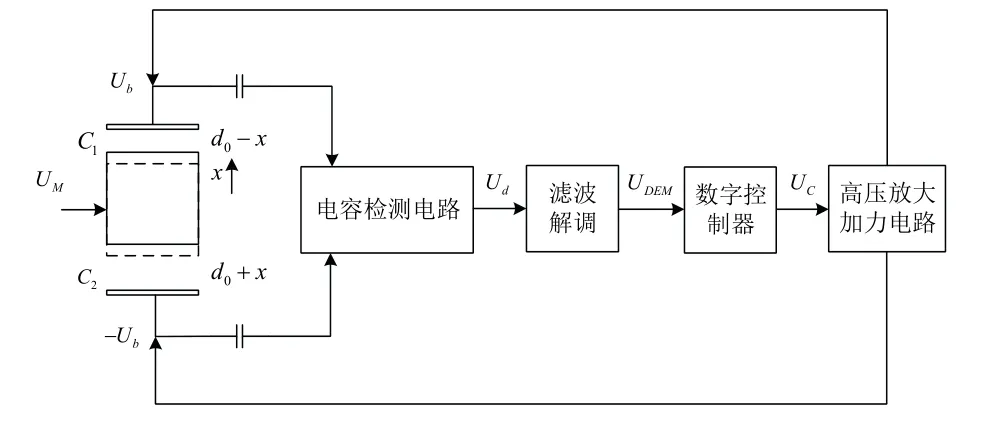
图1 单自由度加速度计系统组成示意图Fig.1 System composition diagram of single degree of freedom accelerometer

系统的核心部件是敏感质量与电极板结构部分。中心的正方形代表敏感质量，两块电极板位于敏感质量的上下两端。当外界没有加速度输入时，敏感质量利用由上下极板提供的静电力悬浮于系统的零点位置（图中虚线处），其标称间隙为d0。

当外界的加速度发生变化，由于惯性力的影响，敏感质量与两侧极板的间隙发生变化，产生位移x，间隙电容（C1,C2）发生变化产生差值，经由电容检测电路转化为与UM同频的高频信号Ud。随后经过滤波和解调电路，产生能够表征位移变化的信号UDEM。通过控制算法，输出控制信号Uc至高压加力放大电路中，生成高压控制信号Ub。Ub通过电极板调整静电力的大小，将敏感质量块拉回平衡位置。此时反馈信号产生的静电力与惯性力相等，其大小和极性即可表征所测量的加速度输入的数值和方向。

1.1 大表面积质量比的敏感质量及电极结构

地面用静电悬浮加速度计的瓶颈问题为所需支承电压高，同时获得大过载能力和高精度较困难，因此最大限度地提高敏感质量的表面积质量比，将有助于减小支承电压幅值，从而折衷过载能力与精度的矛盾。因此设计了如图2 所示的中心固定有一薄法兰盘的空心薄壁圆筒的敏感质量，兼具加工工艺简单及表面积质量比较大的特点。电极结构如图3 所示，圆筒内外侧与法兰盘两侧布置检测和加力电极。

图2 敏感质量结构Fig.2 The test mass structure

图3 圆盘方向和外圆柱方向的电极结构Fig.3 Electrode structure in the direction of disk and outer cylinder

表1 敏感质量结构参数最终设计值Tab.1 Final design value of structural parameters of the test mass

敏感质量结构参数如表1、表2 所示。设计的间隙为圆盘方向30 μm，圆柱方向40 μm，盘面方向1g重力场中无支承垫情况下所需最大支承电压有效值为150 V，正常工作状态下抗过载能力的理论值为4g。

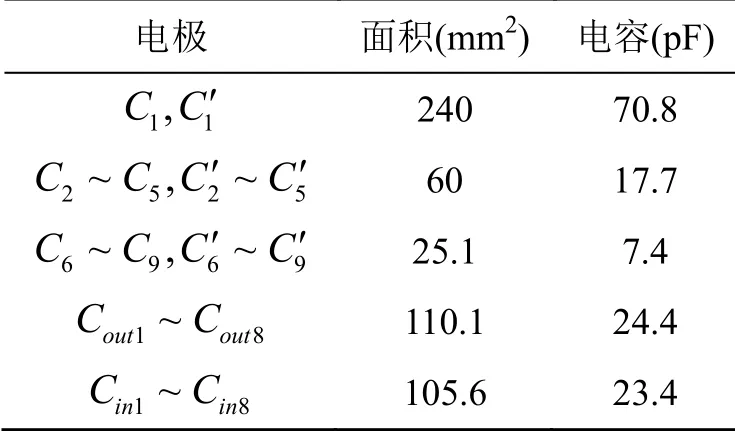
表2 电极面积及电容设计值Tab.2 Electrode area and capacitance design value

1.2 电容检测电极分配方案

由于敏感质量绕Z 轴是几何对称的，因此，设计方案中不对绕Z 轴的旋转角进行位移测量和控制。其它5 自由度的位移和姿态检测有两种方案，第一种是5 自由度均采用盘面电容进行检测；第二种是盘面电容用于Z 方向检测、柱面电容用于其它4 个自由度检测。

具体来说，第一种方法的Z 方向位移使用变间隙式C1和C1′差动电容；X 方向位移使用变面积式的（C6//C′6）和（C8//C′8）差动电容，Y 方向位移使用变面积式的（C7//C′7）和（C9//C′9）差动电容，沿Y 轴旋转 自由度θ方向位移使用变间隙式（C2//C′4）和（C4//C′2）差动电容，沿X 轴旋转自由度φ方向位移使用变间隙式 (C3//C5′)和 (C5//C3′)差动电容。

第二种方法Z 方向位移采用上下盘面的差动电容，X、Y、θ、φ方向利用该方向内外圆柱电极的全部4 个柱面差动电容。

为最大限度地降低支承所需电压，选取的加力电极方案为：每一轴的平动都利用该方向的全部4 通道的电极，转动自由度利用面积乘以力臂最大的方案，即利用圆柱面上的对应电极。两种位移测量方法的各自由度的电极分配汇总见表3 所示。

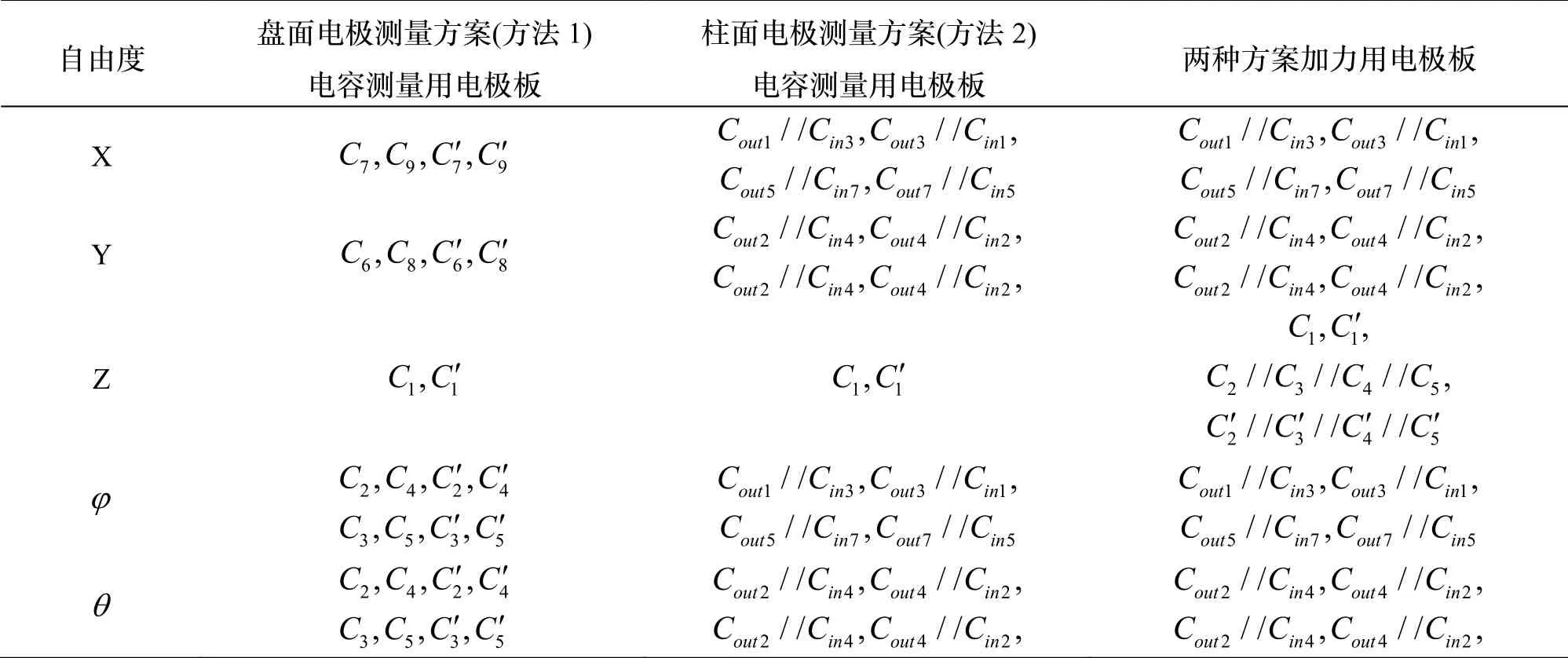
表3 各自由度的电极分配Tab.3 Distribution of electrodes per degree of freedom

方案1 可复用于电容检测高频激励信号的注入电极包括柱面电极和部分盘面电容，位移检测电路激励信号较大，但由于位移测量所用电极面积较小，位移测量电路灵敏度降低；方案2 可利用盘面电极C2～C9作为高频检测信号的注入电极，位移检测电路激励信号较小，但位移测量所用电极面积较大，易获得较高的位移测量电路灵敏度。选择这两种方案中的哪一种，除了要考虑上述工程特点外，还取决于这两种方案对应的加速度计标度因数稳定性、零位稳定性对误差源的敏感度，下面，对敏感探头典型误差源进行分析。

2 敏感质量误差对加速度计性能影响分析

敏感质量圆盘上下表面平行度误差、圆盘与圆柱的垂直度误差是敏感探头加工中的典型误差，会带来位移测量误差、力耦合误差，从而影响加速度计的性能，下面逐一进行分析。

2.1 敏感质量圆盘上下表面平行度误差

下面给出敏感质量圆盘上下表面有平行度误差δ时，在敏感质量不同的位移情况下对各自由度位移测量的影响。

（1）敏感质量圆盘上下表面平行度误差

图4 敏感质量圆盘上下表面不平行示意图Fig.4 Schematic diagram of non parallel upper and lower surfaces of the test mass disk

不失一般性，假定敏感质量盘面的上表面与定电极平行，下表面与定电极之间最大不平行角度为δ，如图4 所示。敏感质量在Z 轴方向发生小量平移时，由于Z 自由度位移敏感电极是一个整圆周，因此不平行度不对电容差产生影响，电容差表达式仍为：

其中ε0为真空介电常数，ε0≈ 8.85 ×10-12F /m；εr间隙介质的相对介电常数，真空下εr≈ 1；A1为C1电极板的有效面积。

（2）对XY 自由度测量的影响

图5 是敏感质量圆盘上下表面不平行时计算变面积位移测量示意图。

图5 敏感质量圆盘上下表面不平行时计算变面积位移测量示意图Fig.5 Schematic diagram of calculating variable area displacement measurement when the upper and lower surfaces of the test mass disk are not parallel

如图5 所示情况下，上极板的电容值不变，下极板的电容值会变化。

此时下极板的电容表达式为：

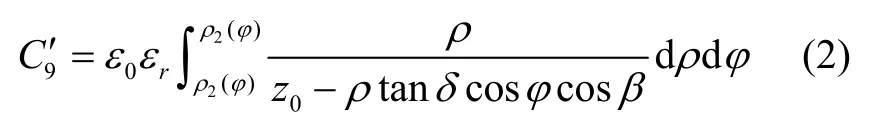
其中，

ρ1（φ） =，ρ2（φ） =R5；R5，R6分别为圆盘外环电极内半径、外半径；φp为外环电极的弧度角；β为不平行度δ相对于X 轴的偏移角，如图6 所示。

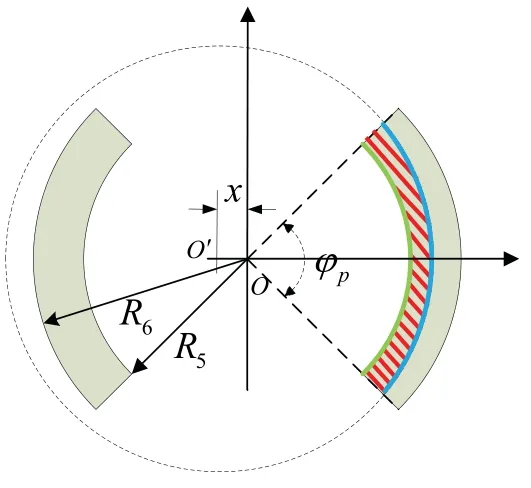
图6 变面积位移测量示意图Fig.6 Schematic diagram of variable area displacement measurement

（3）对 ,θ φ 自由度测量的影响

当表面不平行的敏感质量沿X 轴顺时针旋转角度φ，同时沿Y 轴逆时针旋转角度θ时，下电极板的电容为：

其中，κ′(α) =φsinα- (δ+θ)cosα；R3，R4分别为圆盘中环电极内半径、外半径，R3≤r≤R4；α为中环电极的弧度角。

积分后并与电极板C2的电容求差可得不平行度δ对电容变化的影响为：

可见差动电容与cosβ相关，即随敏感质量圆周方向的位置不同而变化。

（4）对Z 方向静电力的影响

图7 是敏感质量圆盘不平行时的Z 方向受静电力示意图。

图7 敏感质量圆盘上下表面不平行时受力图Fig.7 Force diagram of the test mass disk when its upper and lower surfaces are not parallel

根据静电力公式：

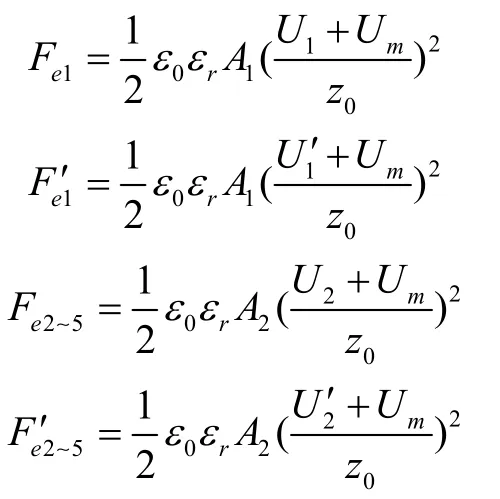
其中，

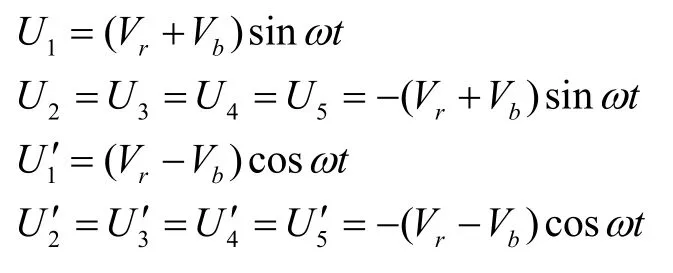
式中Vr为预载电压的幅值，Vb为控制电压的幅值，通常Vr≥Vb；Um为检测信号，ω为检测信号的频率；U1、为C1电极在Z 自由度的控制电压；U2、为C2～5电极在Z 自由度的控制电压；A2为C2～5电极板的有效面积。

可得敏感质量受到的所有上极板的合静电力和下极板的合静电力均为：

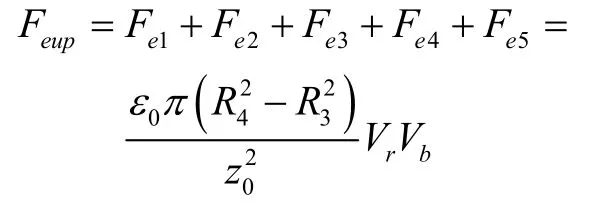
但下极板的合静电力沿X、Y 方向具有分力，分别为：

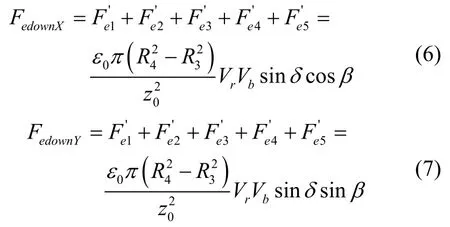
可见，不平行度对Z 方向的加力的幅值没有影响，但由于圆盘不平行，此力的方向并不是沿Z 方向，而是同时有沿盘面法线方向在电极坐标X、Y 平面内投影方向的分力。因此，盘面不平行时，对Z 方向的加力影响为：对X、Y 方向产生力耦合误差，此力耦合误差随着敏感质量旋转而改变。

2.2 圆盘与圆柱垂直度误差

当敏感质量圆盘与圆柱有垂直度误差ε并位移x时，会影响圆柱电极与敏感质量之间的电容和力。以其中一块电极板为例，计算得到间隙电容变为：

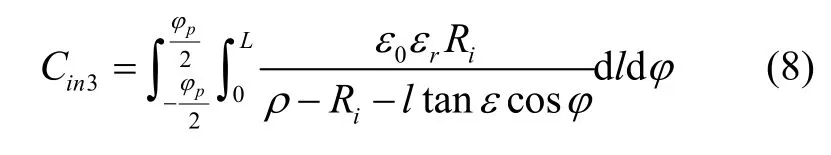
其中Ri为圆柱内电极的半径；Rj为圆柱外电极的半径；L为电极板的长度；ρ为敏感质量位移x后的解析表达式：

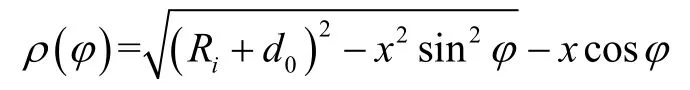
式(8)进行积分、泰勒级数展开可得：

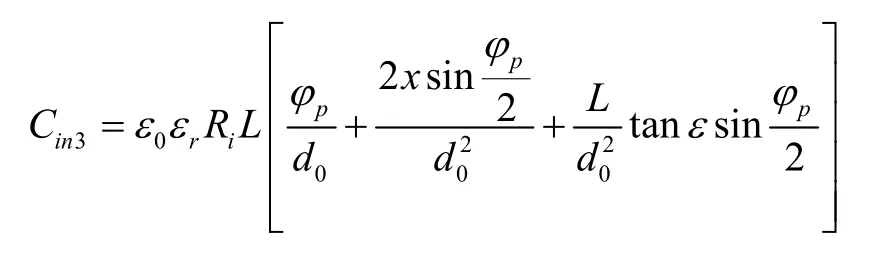
分别计算其余七块电极板的间隙电容可得：

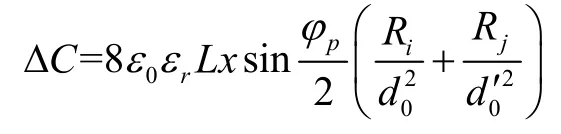
式中d0为敏感质量与圆柱内电极的间隙；为敏感质量与圆柱外电极的间隙。可见，垂直度误差ε对电容变化不产生影响。

对力耦合的影响分析：

图8 是敏感质量圆盘与圆柱有垂直度误差ε时敏感质量所受静电力示意图。

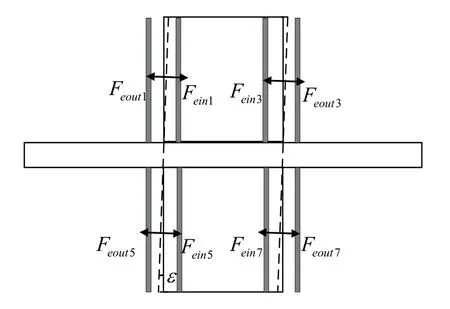
图8 敏感质量圆盘与圆柱有垂直度误差时受力图Fig.8 Force diagram of the test mass disk and cylinder with perpendicularity error

经过计算，得到敏感质量受到的合力为：

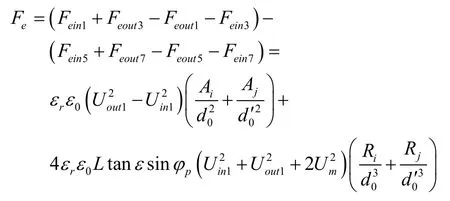
其中，

式中Ai、Aj分别为圆柱内外电极的面积；Ui1n、Uout1分别为圆柱内外电极的控制电压。

则合力可写为：

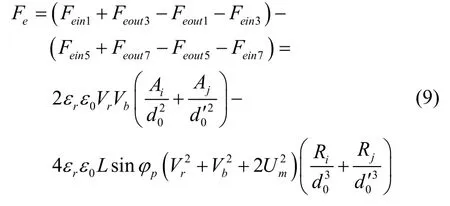
可见垂直度误差对加力幅值不会产生影响，却会带来沿Z 方向的力耦合分量。但在垂直度误差不大的条件下，可通过调节位移测量零位使得圆柱相对于柱面电极平行，使得垂直度误差带来的力耦合影响降到最低。

综上，典型误差源对加速度计的影响为：当敏感质量圆盘上下表面有平行度误差时，对Z 方向的电容测量不产生影响；当采用方法1 的位移测量方案时，对X、Y、θ、φ自由度位移测量均有影响，且影响大小随敏感质量绕圆柱轴线的旋转角度有关；对X、Y 方向产生力耦合误差，此力耦合误差随着敏感质量旋转而改变。

当敏感质量圆盘与圆柱有垂直度误差时，会产生沿Z 敏感轴方向的力耦合，但可通过调节位移测量零位使得垂直度误差对力耦合影响降到最低。

因此，敏感质量加工时应提高盘面平行度、盘面与柱面垂直度的制造精度。

3 静电支承回路仿真设计

为更好的对比两种方案对加速度计性能的影响，设计了一套控制系统仿真软件。首先，在无误差情况下，设计了控制系统PID 参数，其次，引入误差后仿真各误差源对加速度计标度因数、零位的影响。

3.1 控制器模型

以Z 方向为例，整体的控制系统框图如图9 所示。

图9 支承控制系统整体框图Fig.9 Overall block diagram of support control system

系统闭环传递函数可表示为

系统刚度的表达式为

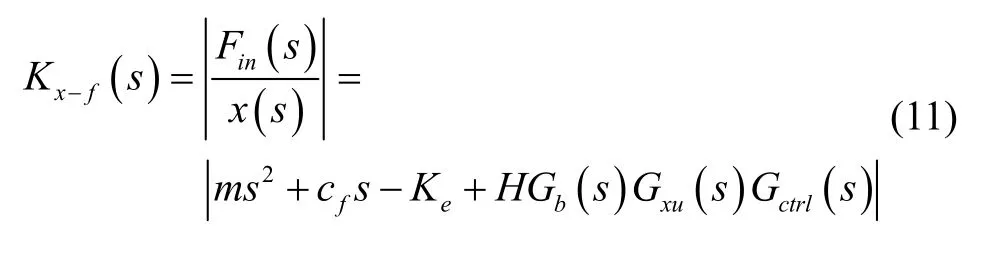
设计时，首先根据表4 计算各自由度静电加力系数。根据表5 计算各自由度静电负刚度，然后根据支承系统闭环传递函数设计PID 控制器，使PID 控制器的参数兼顾动态与静态性能指标要求，满足系统稳定性和准确性及具有足够的刚度。

表4 静电加力系数表达式Tab.4 The expression of electrostatic applied force coefficient

表5 静电负刚度表达式Tab.5 Electrostatic negative stiffness expression

根据表4、5 及结构参数，计算得到Z 自由度的参数如表6 所示。

表6 系统参数Tab.6 System parameter

控制采用PID 控制器，硬件条件为：位移检测电路带宽为20 kHz，高压放大电路带宽10 kHz，数字控制器采样周期和运行时间延迟分别为50 μs 和25 μs，以此构建其滞后环节模型。控制电压输出范围±5 V，放大倍数Kb为100。所设计的控制器为：

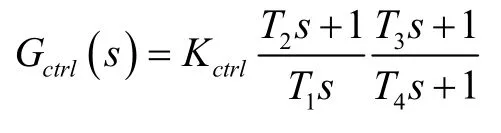
Kctrl=300,T1=1/0.85,T2=1/500,T3=1/700,T4=1/30000。

仿真所得回路主要性能参数如表7 所示。可以看到，开环相位裕量在47.1 °，具有稳定性保证，支承刚度是固有负刚度的2.74 倍。

表7 各回路主要性能参数Tab.7 Main performance parameters of each circuit

3.2 闭环控制回路的Simulink 模型

根据加速度计工作原理和误差源对位移测量和加力的影响，建立了如图10 所示的Simulink 仿真模型。其工作流程如图11 所示。

图10 闭环控制的Simulink 建模流程Fig.10 Simulink modeling process of closed loop control

图11 闭环控制的Simulink 模型Fig.11 Simulink model of closed loop control

在无误差源的情况下，从1g重力场下起支到Z自由度方向上阶跃输入，θ、φ自由度方向上阶跃输入为时，两种检测方案的敏感质量Z 自由度位置与反馈电压变化仿真结果，如图12-13所示。

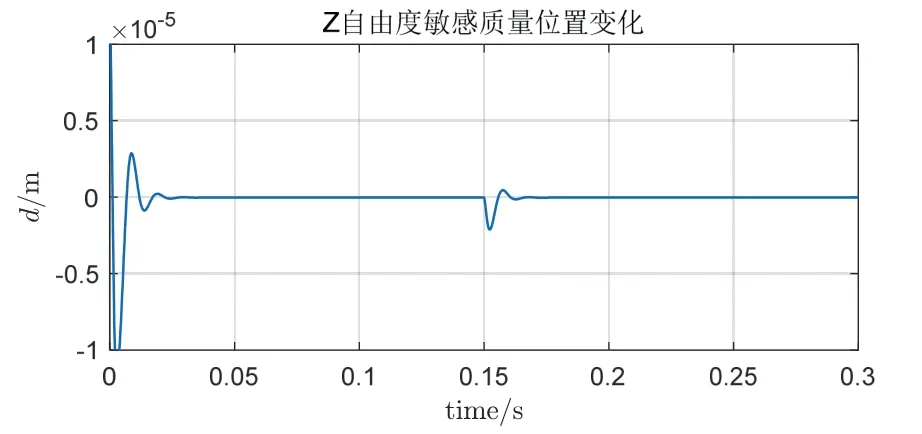
图12 理想状态下敏感质量位置与反馈电压变化Fig.12 Position of sensitive mass and change of feedback voltage in ideal state

图13 理想状态下反馈电压变化Fig.13 Feedback voltage change in ideal state

在不考虑检测电路噪声的情况下，当控制达到稳定时，稳态误差为 1.7 ×10-17m，说明控制器能够满足系统的稳定性和准确性的要求。

4 典型误差源下不同测试方案的仿真

针对盘面电极和柱面电极两种位移姿态检测方案进行了仿真。

对敏感质量圆盘不平行角度误差δ=0.01°，圆盘与圆柱无垂直度误差情况、圆盘与圆柱垂直角度误差ε= 0.01°，圆盘无不平行度误差两种情况分别进行仿真，Z 自由度方向上的输入从-1g到1g，分别计算存在误差源时两种测量方案下的标度因数稳定性，结果如图14-16 所示。

图14 δ= 0.01 °, ε = 0°盘面电极测量方案标度因数稳定性Fig.14 δ= 0.01 °, ε = 0°Stability of scale factor of disk electrode measurement scheme

图15 δ= 0.01 °, ε = 0°柱面电极测量方案标度因数稳定性Fig.15 δ= 0.01 °, ε = 0°Stability of scale factor of cylindrical electrode measurement scheme

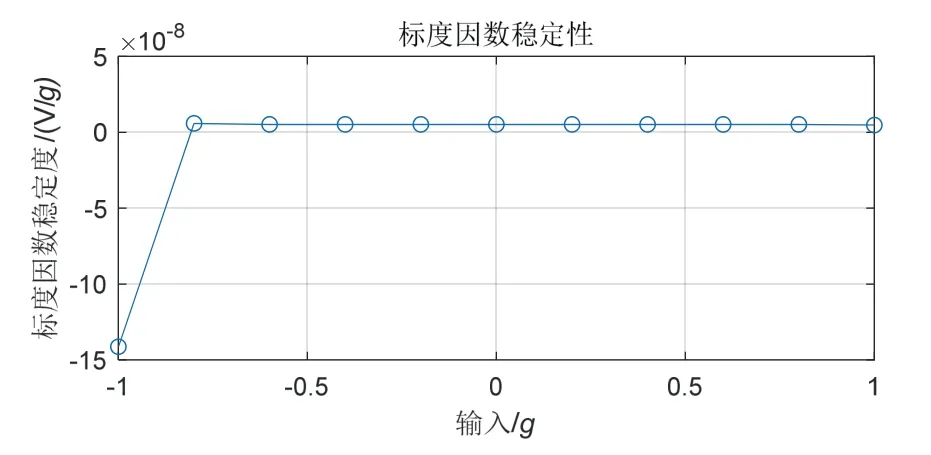
图16 δ= 0 °, ε = 0.01°盘面电极测量方案标度因数稳定性Fig.16 δ= 0 °, ε = 0.01°Stability of scale factor of disk electrode measurement scheme

图17 δ= 0 °, ε = 0.01°柱面电极测量方案标度因数稳定性Fig.17 δ= 0 °, ε = 0.01°Stability of scale factor of cylindrical electrode measurement scheme

可见存在敏感质量圆盘不平行度误差δ时，采用柱面电容检测方案可获得更优良的标度因数稳定性，标度稳定性可达10-9V/g量级，比采用盘面电极提高了一个数量级。存在圆柱垂直度误差ε时，同时可通过调节位移测量零位使垂直度产生的影响降到最低，获得更优良的标度因数稳定性。综上所述，在工程中选择柱面电极作为敏感质量位移与姿态检测的测量电极。

5 结 论

本文针对加速度计地面应用的迫切需求，提出了一种适合地面应用环境的高精度三轴静电加速度计方案，并基于MATLAB/Simulink，建立了一套三轴静电悬浮加速度计控制系统仿真模型，比较了分别采用盘面电极与柱面电极作为敏感质量位移与姿态检测的测量电极时，典型误差源对加速度计标度因数的影响程度。仿真结果表明，采用柱面电极用于位移测量，可获得更优良的标度因数稳定性，因此在工程中选择柱面电极作为敏感质量位移与姿态检测的测量电极。

未来的工作中将开展静电悬浮加速度计的地面试验研究和性能评估。