基于粒子群优化的舰船捷联惯导初始对准方法

徐 博，赵晓伟，金坤明

（哈尔滨工程大学 智能科学与工程学院，哈尔滨 150001）

舰船惯性导航是一种完全自主的导航方式，由于不需要外界的任何信息以及不向外界传递电磁波等特点，被广泛应用于多个领域[1]。初始对准技术是捷联惯导系统关键技术之一，初始对准的好坏直接影响到惯导解算的精度[2-3]。为了提高初始对准的精度，减少初始对准的时间，近年来，很多学者围绕着捷联惯性导航系统的初始对准开展了大量的研究。朱兵等提出了一种利用粒子群算法对罗经回路参数进行寻优的方法，该方法相对于传统的根据经验以及大量的反复试验确定罗经回路参数而言，节约了大量的时间[4]，谢祖辉等提出了一种基于粒子群优化算法的参数辨识法，该方法解决了基座摇摆运动条件下，用递推最小二乘参数辨识法对初始失准角进行估计时，存在方位失准角收敛速度慢、估计精度受到北向失准角估计精度影响等问题[5]。严恭敏等也开创性地提出逆向导航概念，并结合罗经法，达到了缩短对准时间的目的[6]。孙立江等针对激光捷联惯导晃动基座下受载体运动干扰难以实现粗对准这一问题，提出了一种惯性系下基于多矢量定姿的粗对准方法，有效地抑制了干扰运动对对准精度的影响，建立了更准确的捷联矩阵，同时使对准结果具有更好的稳定性[7]。

为了对惯性系对准算法进行深入探索，本文针对使用多矢量定姿的惯性系对准方法时航向角收敛速度慢的问题，利用粒子群算法对惯性系对准方法进行优化，并进行了转台试验验证，试验结果表明所提算法的有效性。文章的结构安排为：第一部分给出坐标系的定义并介绍了惯性系多矢量的对准方法；第二部分首先给出了粒子群算法，然后给出优化算法所用到的粒子群适应度函数以及粒子早熟问题的解决方案；第三部分进行转台摇摆试验验证，并对试验结果进行分析；第四部分给出结论。

1 矢量定姿对准方法

1.1 坐标系定义

（1）地球坐标系（e系）：坐标原点取在地球中心，oxe轴在赤道平面与载体当地子午面的交界线上，oze沿极轴方向，oxe轴、oye轴和oze轴构成右手坐标系[8]。

（2）选取“东-北-天”坐标系为导航坐标系（n系）。

（3）定义“右-前-上”坐标系为载体坐标系（b系）。

（4）地心惯性坐标系（i系）：在初始对准起始时刻，oxi轴在当地子午面且平行于赤道平面，ozi指向地球自转方向，三轴构成右手坐标系，初始对准后i系三轴相对惯性空间保持不动。

（5）初始时刻惯性坐标系（ib0系）：在起始时刻ib0系重合于b系，初始对准后ib0系不随捷联惯组转动，即在惯性空间中保持指向不动。

1.2 惯性系多矢量对准算法

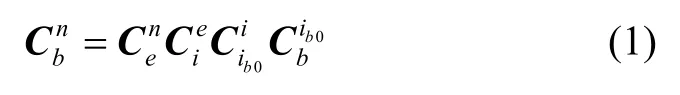
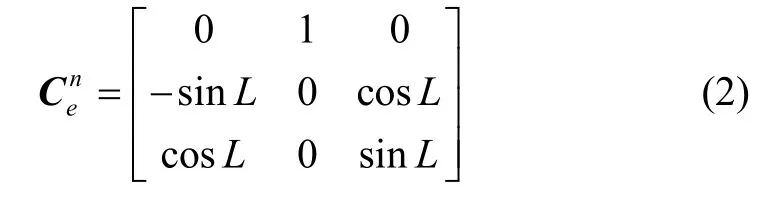
L为载体所在位置的纬度。

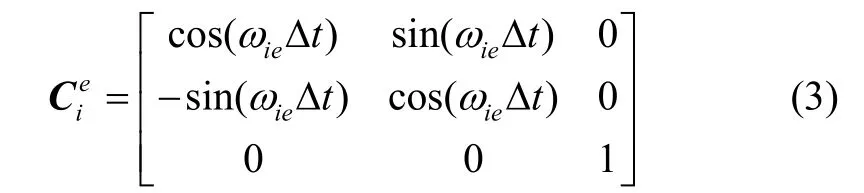
ωie为地球自转角速度， Δt=t-t0为距对准起始时刻的时间间隔。

利用陀螺仪输出的角速度信息，可由式(4)求得载体坐标系相对载体惯性系的旋转矩阵即

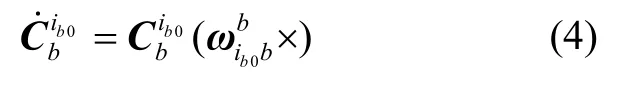
捷联惯导比力方程如下所示：

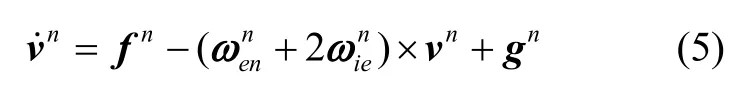
对比力方程进行变形得：

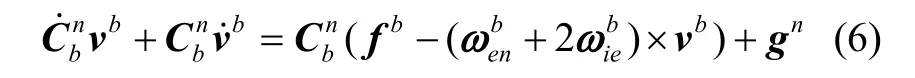
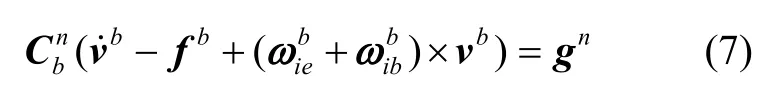
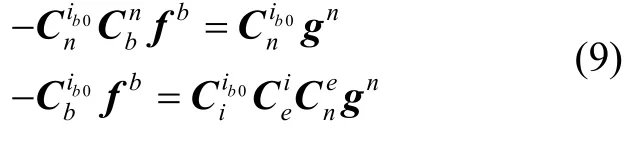
为了减低加速度计测量干扰的影响，将式(9)两边在 [t0,tk]内积分，由于gn= [0 0 -g]T，则重力加速度在地心惯性系下的投影为：

对式(10)进行积分得：

选择m个时刻的速度vi、vib0作为参考矢量，构造目标方程得：

整理变形得：

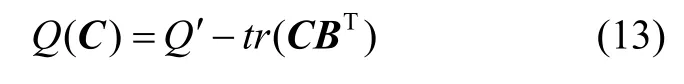
式中，tr(⋅)表示对矩阵的求迹运算。

其中：

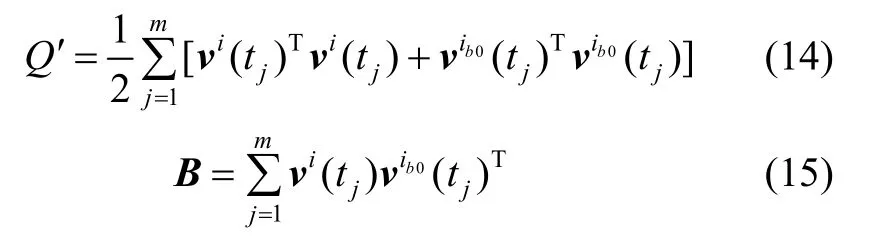
对B进行奇异值分解，得：

式中：U1和U2为正交矩阵；S=diag(s1,s2,s3)，s1≥s2≥s3≥ 0。

使Q取最小值的最优解：

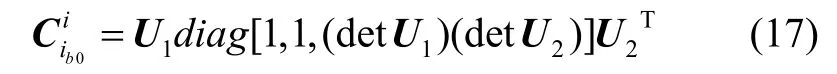
此时进行舰船载体坐标系对导航坐标系姿态矩阵的更新：

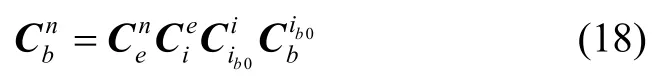
2 优化的惯性系对准算法

2.1 粒子群优化算法

粒子群优化算法通过事先设置一群粒子，并让群体中的每个粒子通过不断地跟踪两个极值和来更新自己的位置和速度，从而降低参数辨识过程中初始值选取的不恰当对收敛速度的影响，最终提高系统初始对准的速度[10-11]。其中，称为个体最优，是每个粒子自身找到的最优解;称为全局最优，是整个种群目前找到的最优解。每个粒子的速度和位置迭代计算公式如下:

式中，k= 1,2...G，G表示最大的迭代次数；i= 1,2...Size，Size表示种群规模，r1和r2表示0 到1之间的随机数；c1表示局部学习因子，代表个体学习能力，c2表示全局学习因子，代表社会学习能力，二者的取值范围通常为[0，2]；ω(t)表示惯性权重，其值越大越有利于展开全局寻优，越小越有利于局部寻优，取值范围通常为[0，1]；Vi表示第i个粒子的速度；Xi表示第i个粒子的位置；pi表示个体最优位置；BestSi表示群体最优位置[12]。粒子群算法的步骤如下：

（1）设置粒子群参数并对其初始化；

（2）计算每个粒子适应度函数值；

（3）更新个体和群体最优解；

（4）通过式（19）计算粒子的速度和位置；

（5）重复步骤（2）-（4）；

（6）达到最大迭代次数，结束粒子群算法，输出待估参数。

用粒子群算法使适应度函数取得全局最小值从而辨识最优的航向角的基本流程如图1 所示。

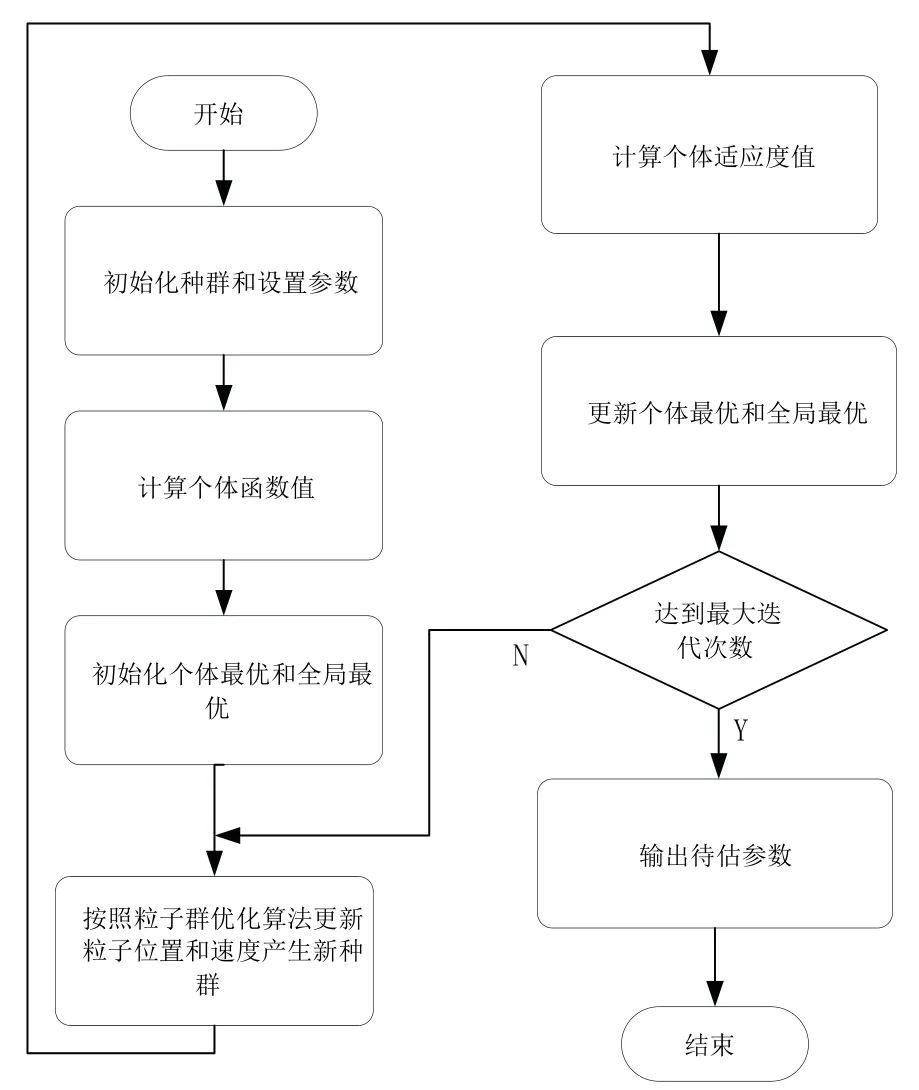
图1 粒子群算法流程图Fig.1 Flow chart of particle swarm optimization algorithm

2.2 粒子群适应度函数的建立

针对惯性系对准算法航向收敛速度慢的问题，考虑到粒子群算法估计参数较多时，对适应度函数要求较高等因素，而且惯性系对准算法水平姿态收敛较快，故本文采用惯性系对准算法对水平姿态进行估计，将载体的航向作为粒子群算法的待估参数。由姿态角计算得到姿态矩阵由式（20）计算得：

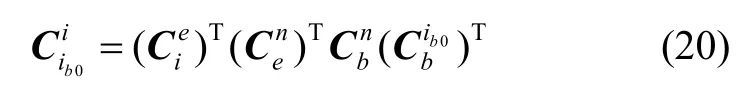
通过vi、vib0和建立误差方程如下：

选择速度误差量的平方和作为粒子群算法适应度函数，适应度函数表示为：

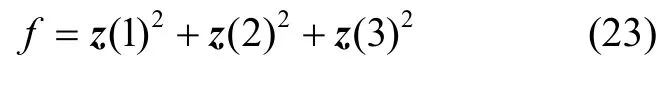
式(23)中，z(1) 、z(2) 、z(3) 为向量z中的元素，由适应度函数可知当用粒子群算法估计的航向角越接近真实航向角时，适应度函数值也就越小。所以利用粒子群算法不断更新载体的航向角，使得适应度函数达到最小值，得到当前时刻最优估计的航向角。

2.3 粒子早熟收敛问题的解决

对于粒子群中的任意粒子，其最终收敛位置将是整个粒子群找到的全局极值。如果粒子群找到的全局极值只有一个，那么所有粒子都会“聚集”到该位置;如果全局极值不止一个，那么粒子将随机聚集在这几个全局极值位置。全局极值是所有粒子在算法运行过程中找到的最佳粒子位置，该位置并不一定就是搜索空间中的全局最优点。若该位置为全局最优点，则算法达到全局收敛，否则算法陷入早熟收敛。针对舰船不具备较强机动能力的特点，可以通过设置航向变化角速率阈值来解决粒子早熟问题。对于系泊状态下的船舶，由于存在一定规律的低频线晃动，所以本文设置载体最大角速率为0.09 rad/s。

如果当前时刻载体的艏摇角速率超过设定的载体最大角速率，则可以判断粒子陷入早熟收敛状态，此时去除掉当前时刻全局最优点所求的，利用前一时刻全局最优点所求的代替。利用粒子群优化的舰船初始对准流程图如图2 所示。

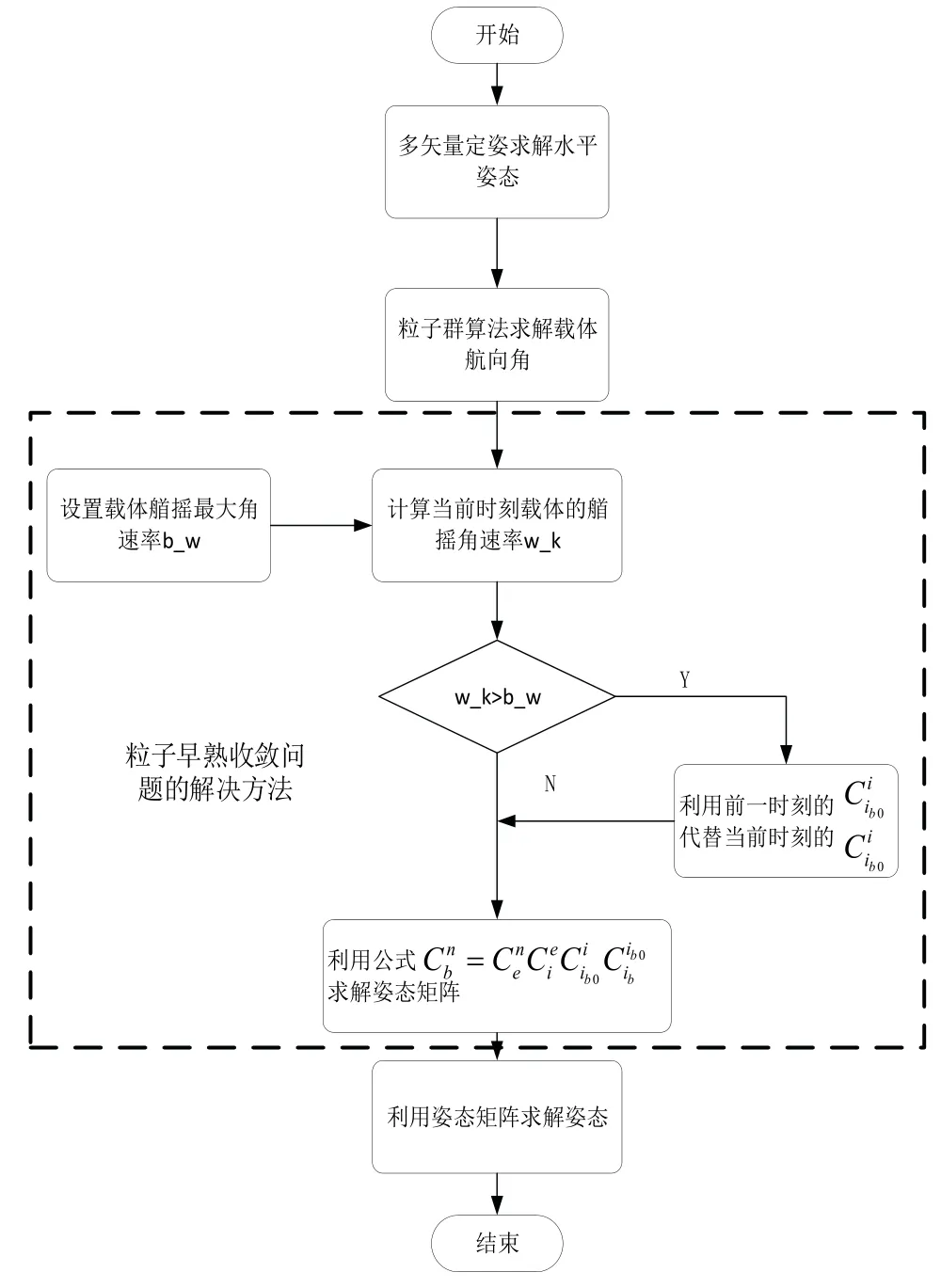
图2 粒子群优化的舰船初始对准流程图Fig.2 Particle swarm optimization for initial ship alignment flowchart

3 转台试验验证与分析

3.1 试验设备及指标

试验转台为SGT-8 型三轴惯导测试转台，附带一台转台控制计算机，转台具有自动闲置、定位、增量、速率、摇摆等功能。转台实物图如图3 所示，转台的主要性能指标如表1 所示。

图3 SGT-8 型三轴惯导测试转台和惯性测量单元Fig.3 SGT-8 triaxial inertial navigation test turntable and inertial measurement unit

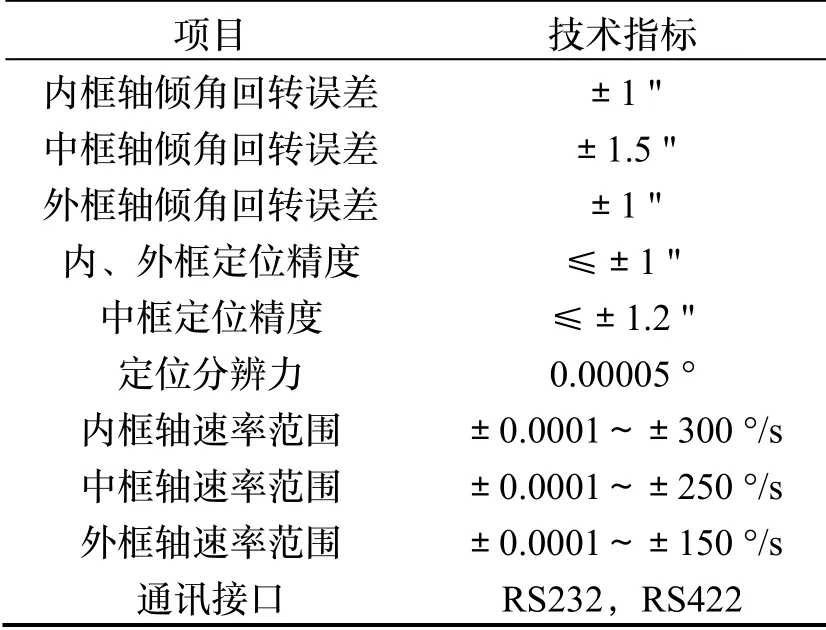
表1 SGT-8 型三轴转台主要性能指标Tab.1 Main performance index of SGT-8 triaxial turntable

3.2 试验结果与分析

为了验证粒子群算法优化的初始对准方法的有效性，进行双轴转台试验，即转台外框固定，内、中框做摇摆运动。转台参数设置如下：航向角设定为225 °；纵摇摇摆幅值设定为14 °，摇摆周期为5 s；横摇摇摆幅值设定为3.7 °，摇摆周期为8 s；运行时间设定为600 s，当地纬度为45.7755 °，当地经度为126.6820 °。所采用的光纤惯性导航系统的器件参数如下：陀螺漂移为0.01 °/h，加速度计零偏为 1 ×1 0-4g。

粒子群参数设置为：种群规模Size=20，最大迭代次数G=150，粒子运动的范围为[0 2π]，粒子运动的速度的范围为[-0.5 0.5] rad。转台试验结果如图4～10 所示。

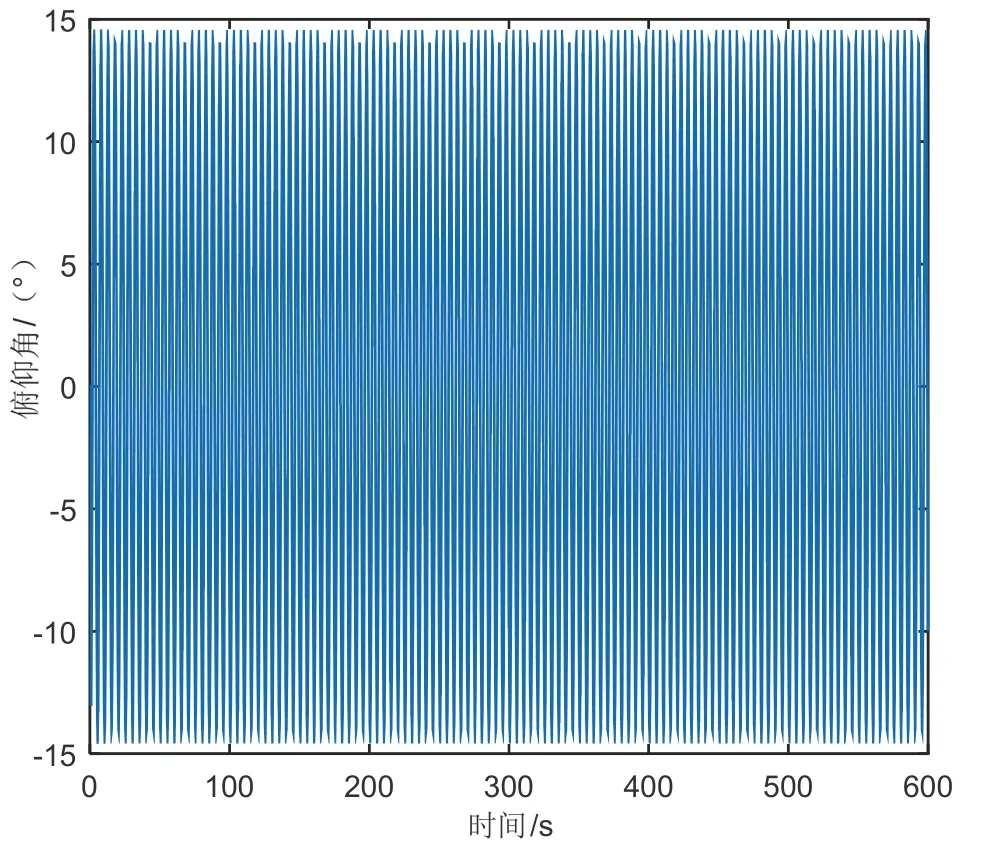
图4 转台中框摇摆运动状态Fig.4 Swaying motion of the frame in the turntable

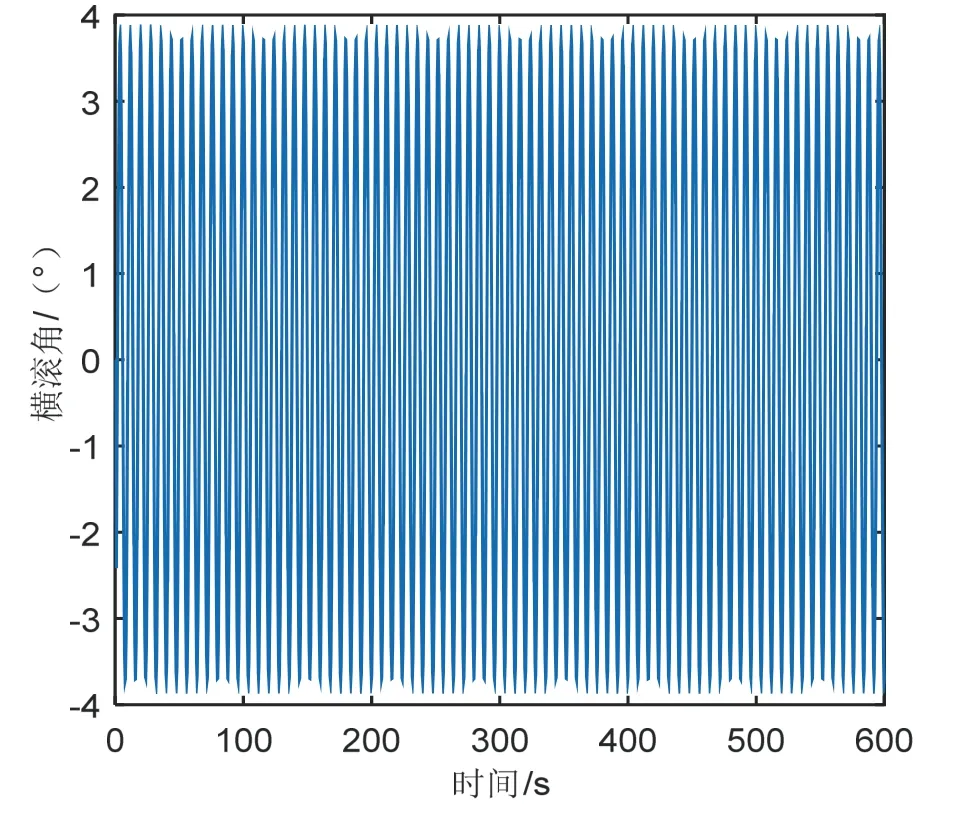
图5 转台内框摇摆运动状态Fig.5 The state of motion of the inside frame of a turntable

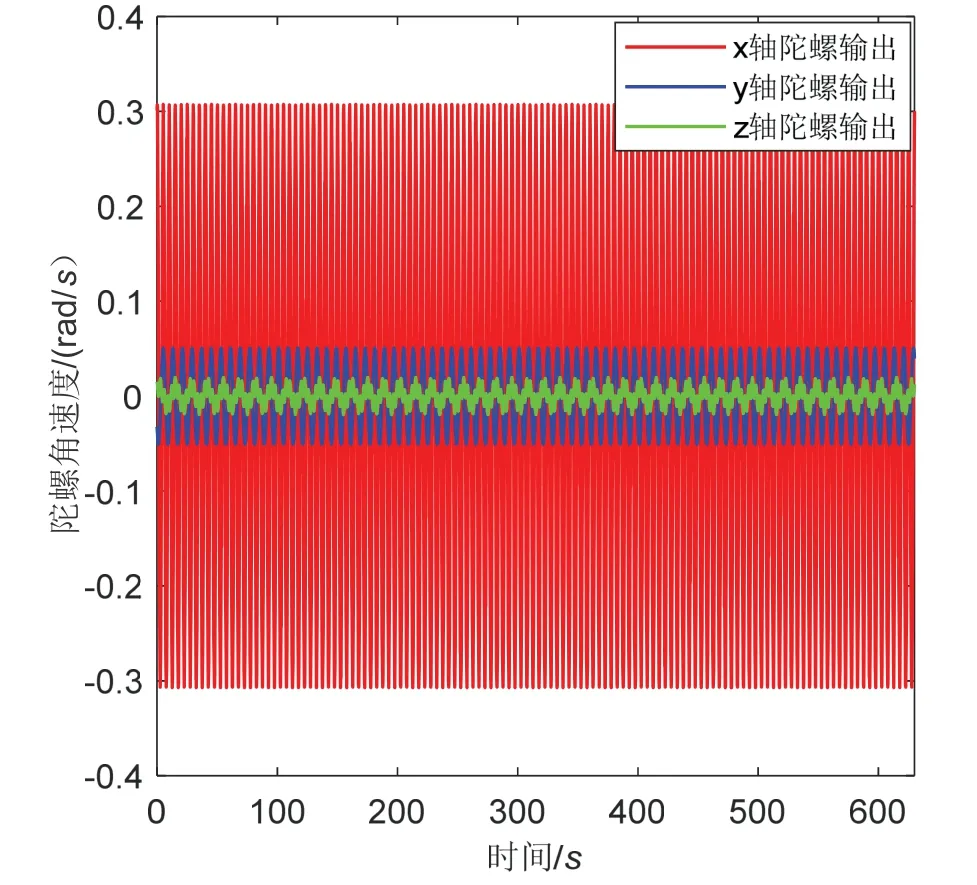
图6 陀螺角速度输出Fig.6 Gyro angular velocity output

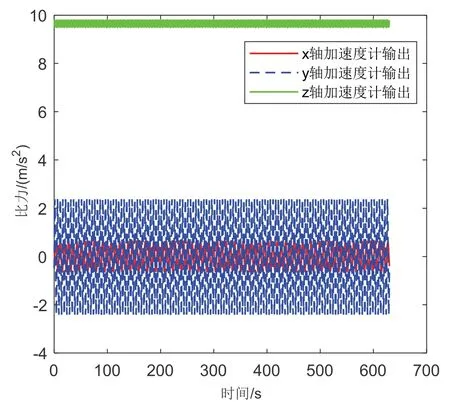
图7 加速度计比力输出Fig.7 Accelerometer specific force output

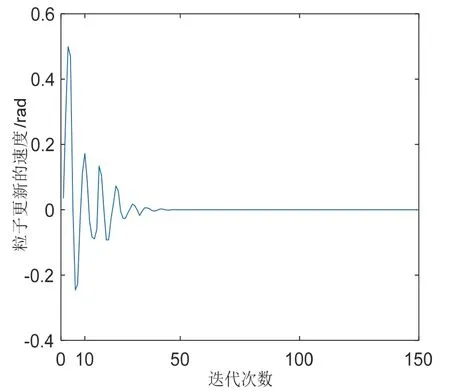
图8 粒子更新速度曲线Fig.8 Particle update speed curve

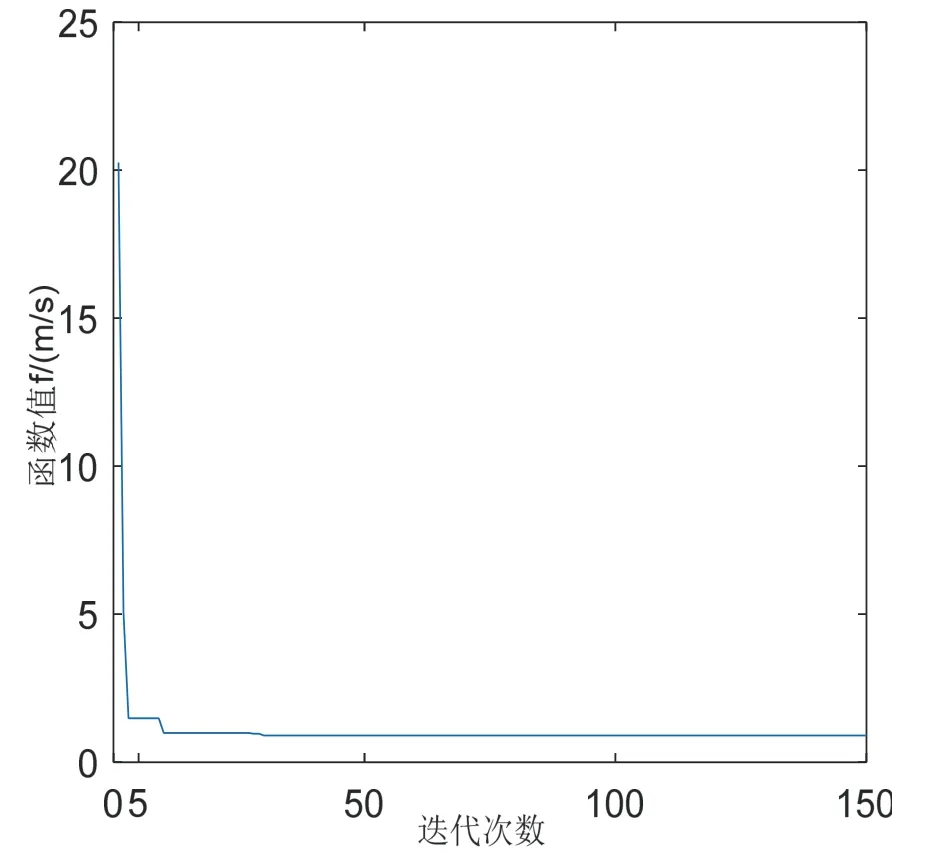
图9 粒子更新适应度函数值曲线Fig.9 Particle update fitness function value curve

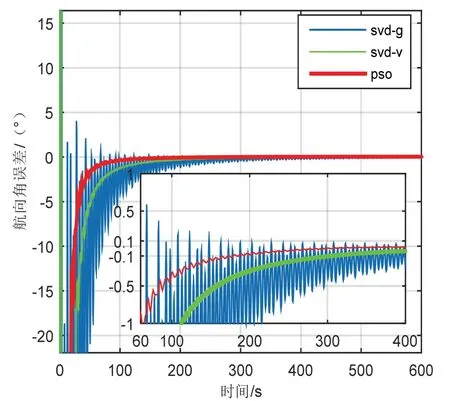
图10 对比对准航向角误差曲线Fig.10 Contrast the alignment Angle error curve

表2 三种对准方法用时对比表Tab.2 Time comparison table of three alignment methods

转台试验结果分析如下：

（1）图4 为转台中框摇摆运动状态图，从图可得转台运动的俯仰角幅值为14 °，运动周期为5 s。图5为转台内框摇摆运动状态图，从图可得转台运动的横滚角幅值为3.7 °，摇摆周期为8 s。由图4、图5 可知转台的运动状态与设定值保持一致；

（2）图6 为陀螺仪角速度输出结果，结果显示x、y、z 三轴陀螺仪角速度输出幅值分别为0.31 rad/s、0.05 rad/s、0.02 rad/s。图7 为加速度计比力输出结果，结果显示x 轴比力输出为(-0.6～0.6)2m/s ，y 轴比力输出为(-2.4～2.4) m/s2，z 轴比力输出为(9.5～9.8) m/s2；

（3）图8 为粒子更新速度结果，可以看出粒子群更新速度在粒子运动的速度范围[-0.5 0.5] rad 内不断减小，直至迭代到第50 代时粒子更新速度趋向于零并保持稳定。图9 为粒子更新适应度函数值的结果，粒子更新适应度函数值最初为20 m/s，更新到第5 代时适应度函数值减小至1.8 m/s，适应度函数值下降速度非常快。从图8、图9 中可以看出通过粒子群算法只需要迭代50 次就可以找到该时刻的全局最优解，粒子群算法能够快速地找到目标函数值；

（4）为了更加有效地验证粒子群算法的优越性，引入了svd-v 和svd-g 两种对准方法进行比对，其中svd-v 是以vi、vib0作为参考矢量的基于多矢量定姿的惯性系对准方法，svd-g 是以gi、gib0作为参考矢量的基于多矢量定姿的惯性系对准方法。图10 为三种初始对准航向角误差曲线对比图，表2 根据图10 的误差曲线列写了三种初始对准方法在不同对准航向角误差条件下的所用时间。可以看出，基于svd-v 的初始对准方法优于基于svd-g 的初始对准方法，当使初始对准航向误差角＜0.5 °时，svd-v 算法相比svd-g 算法对准时间缩短了44%，当使初始对准航向误差角＜0.1 °时，svd-v算法相比svd-g 算法对准时间缩短了21%。基于粒子群优化的惯性系对准算法明显优越于与其对比的两种对准方法，当使初始对准航向误差角＜0.1 °时，基于粒子群优化的惯性系对准算法相比基于svd-g算法对准时间缩短了56%。

综上，三种方法虽然稳态精度相当，航向角误差均小于0.1 °，达到了0.01 °/h 的光纤陀螺精度对应的稳态对准精度。但是基于惯性系的粒子群算法优化的初始对准方法收敛速度明显优于多矢量定姿的惯性系对准的两种方法，对于缩短舰船的初始对准时间具有重要意义。

4 结 论

舰船初始对准的结果对于舰船捷联惯导系统后续的导航定位至关重要，为了快速、准确地得到舰船初始对准结果，本文所提方法首先通过基于多矢量定姿法对水平姿态进行对准，然后利用基于惯性系的粒子群优化的初始对准算法对航向角进行对准，试验结果表明：粒子群优化算法能够快速准确地得到待估航向角，有效缩短初始对准时间，达到光纤陀螺对应的稳态对准精度指标。