基于自适应积分反步法的四旋翼无人机抗干扰轨迹跟踪控制

陈志明，刘龙武，刘 瑞，骆州淮

（南京航空航天大学 航天学院，南京 210016）

近年来，无人飞行器，因其便捷、低成本等优点已得到广泛应用与发展，四旋翼作为无人飞行器的一种，具有体积小、垂直起降、操作简单等优点，也成为航空领域的研究重点之一。

四旋翼无人机因其体积小、非线性、且为欠驱系统，对不确定干扰因素敏感，包括：风力扰动、空气摩擦以及自身的不确定性参数。针对四旋翼无人机，研究人员已进行了许多相关研究并提出了一些鲁棒性较好的控制系统，如干扰抑制控制[1]，模糊逻辑控制[2]、反步法控制[3,4]、LQR(linear quadratic regulator)控制[5,6]、滑模控制[7,8]等，但是，不确定外界干扰仍是四旋翼控制的关键点。如Linxing Xu，Hongjun Ma提出级联有源干扰抑制控制作为无人机姿态控制分系统，此方案可一定程度上减少外界干扰带来的影响，提高飞行稳定性，但应用于轨迹跟踪控制时，对位置回路的干扰抑制较弱，无法保证轨迹跟踪的准确性；Qi Lu，Beibei Ren[9]，Alberto Castillo[10]，Nigar Ahmed[11]，Ning Wang[12]等设计了干扰观测器估计外部不确定干扰和系统的不确定性，此方案可有效减少外部干扰带来的影响，但是，干扰感测器使得控制器结构复杂，且会带来数据延迟；Tianpeng Huang[13]，Hakim Bouadi[14]，V.T. Hoang, M.D. Phung[15]等提出自适应滑模控制器消除高度和姿态跟踪误差，Justin M.Selfridge[16]提出模型参考自适应控制应用于无人机姿态通道控制，Anastasia Razinkova[17]采用自适应补偿方案减小外界干扰引起的无人机位置跟踪误差，虽然自适应补偿因子可有效估计外界干扰项，减小控制误差，但无人机指令跟踪的速度与准确性仍是无人机控制的亟待解决的关键问题。此外，神经网络也被广泛应用于无人机的干扰补偿，如：Hadi Razmi[18]提出基于自适应神经网络的滑模高度控制器减小高度误差；Jesús Enrique Sierra，Matilde Santos[19]提出自适应神经网络估计器有效抑制风力和有效载荷干扰；Yanmin Chen，Yongling He 设计了分散的PID 神经网络控制有效抵抗外界风力干扰，保证稳定性。虽然神经网络结构的引入可实现更精确的不确定性干扰项的估计与补偿，但神经网络结构的复杂性必定会增加控制率计算量，加重无人机控制器负担，实时性难以保证。因此，如何有效解决外界不确定干扰影响，并保证无人机的轨迹精确跟踪仍是无人机控制的关键难题。

本文提出一种位姿双回路自适应积分反步法实现无人机的轨迹精确跟踪，其中自适应因子可有效补偿外界不确定性干扰带来的影响，同时，姿态回路控制器中加入了积分因子，可保证姿态回路指令跟踪的准确性和稳定性。此方案可有效提高无人机的轨迹跟踪能力，并保证无人机具有良好的鲁棒性和稳定性。

1 动力学模型建立

本文基于Parrot Minidrone 建立四旋翼无人机动力学模型，如图1 所示。四旋翼利用四个电机不同的组合实现自身的俯仰、横滚、偏航和升降运动，如表1 所示。其中“+”表示电机的转速增加，“-”表示电机转速减小。假定四旋翼无人机为一个均匀对称的刚体，由牛顿欧拉动力学算法可得到四旋翼的动力学模型如下[20]：

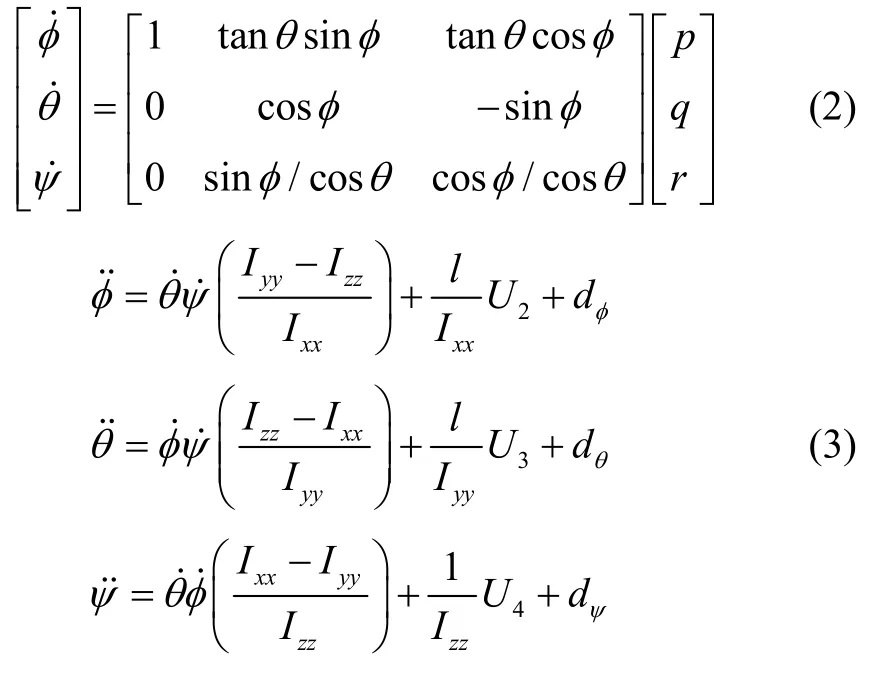
其中，x，y，z，φ，θ，ψ分别表示无人机的3 个位置状态量和3 个姿态角状态量；p，q，r表示无人机滚转、俯仰和偏航三通道的姿态角速度变化量；Ixx，Iyy，Izz为四旋翼的三轴转动惯量；m为无人机质量；l表示机体中心与旋翼中心的距离；U1，U2，U3，U4分别为四旋翼虚拟控制变量；g为重力加速度；dx，dy，dz，dφ，dθ，dψ表示无人机6 通道的不确定性干扰变量。

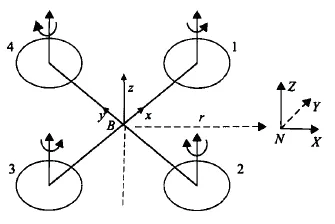
图1 四旋翼动力学模型Fig.1 The dynamic model of quadrotor

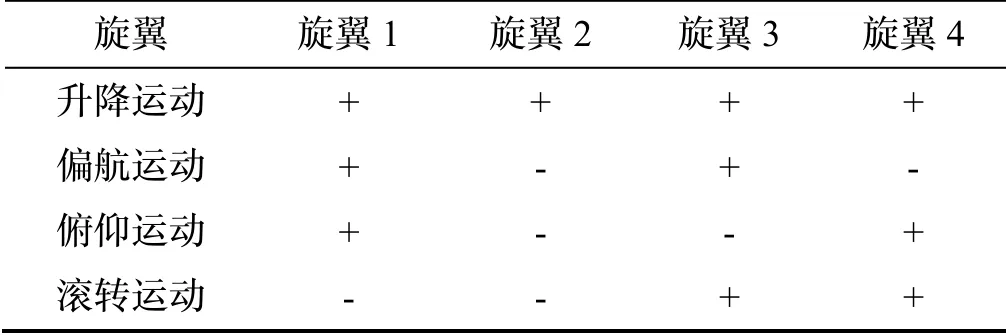
表1 四旋翼电机转速与飞行动作关系Tab.1 The relationship of the four rotors and flying action

2 控制器设计

四旋翼无人机是一个多变量非线性欠驱动系统，包括4 个虚拟控制输入变量和6 个状态输出变量。假定四旋翼为一个严格对称系统，则高度控制与偏航控制可以作为独立的控制通道，俯仰、滚转和水平位置控制通道间相互耦合，4 个虚拟控制输入变量U=U1+U2+U3+U4与6 个状态输出变量(x，y，z，φ，θ，ψ)的关系可表示为：

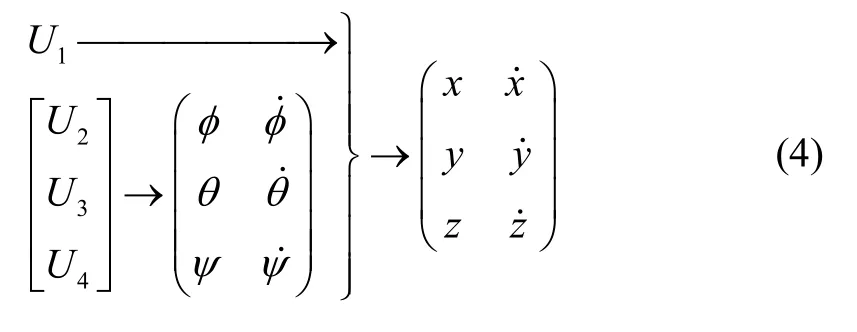
当U2，U3，U4已知时，姿态角和姿态角速度可由式(2)(3)反推得到，当U1，U2，U3，U4已知时，则x，y，z，可根据式(1)-(3)得到。因此，本文设计了一个基于自适应积分反步法的双回路位姿控制系统，如图2 所示。位置回路控制可保证四旋翼无人机快速响应跟踪指令并准确跟踪，姿态回路可解耦姿态与位置通道，同时保证四旋翼飞行的稳定性。自适应积分反步法可减少外部不确定性干扰给控制系统带来的影响，提高四旋翼无人机控制系统的鲁棒性。

图2 基于自适应积分反步法的四旋翼双回路控制系统Fig.2 The general block diagram of the dual-loop control system

图2 中，Ux，Uy表示位置回路的虚拟控制输入变量：

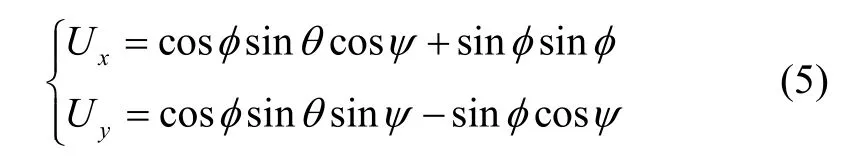
假定偏航角ψ已知，则期望滚转角φd与期望俯仰角θ d可根据式(5)反推得到，

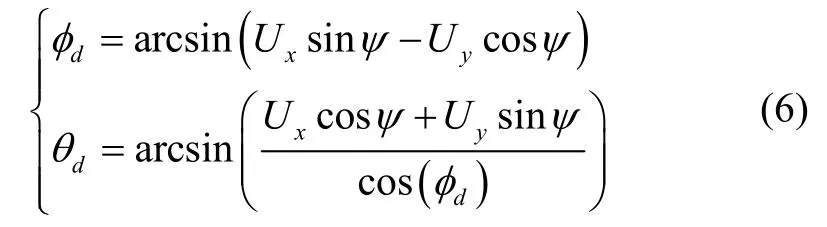
2.1 位置回路控制器设计

为减少外部不确性干扰因素对轨迹跟踪控制的影响，本文在传统反步法控制器的基础上，增加了自适应因子，设计了一种自适应积分反步法以补偿干扰因素带来的误差，提高飞行控制系统的鲁棒性，保证四旋翼无人机具有良好的飞行效果。

根据式(5)和式(1)，四旋翼Z 通道的动力学微分方程可表示为：

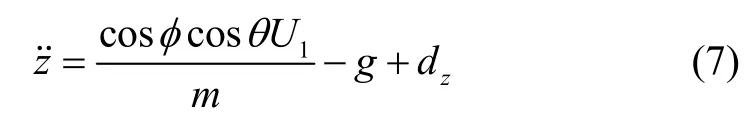
定义Z 轴方向的飞行速度分量为w=，位置误差为e z=z-zd，zd为四旋翼期望位置Z 轴方向的分量，则状态变量z的李雅普诺夫函数可表示为：

状态变量z的李雅普诺夫函数关于时间的微分为：

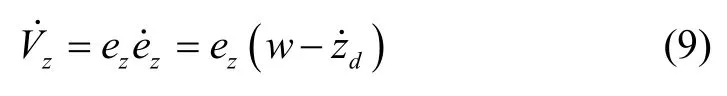
定义Z 轴方向速度分量w为αw，则式(9)可表示为：

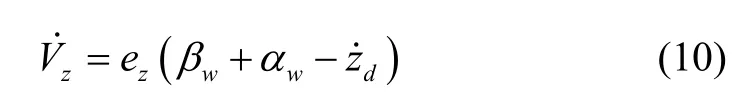
其中，βw为真实值w与w估计值αw的差值。

设定

其中，cz为一个正常数，cz＞ 0，则式(10)可表示为：

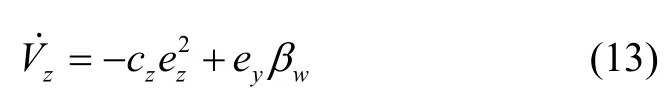
根据李雅普诺夫稳定性理论可知，当βw=0时，式(13)满足则Z通道控制系统稳定。然而，βw为状态估计值与真实值之间的差值，不为零，则需进一步设计控制器。

定义

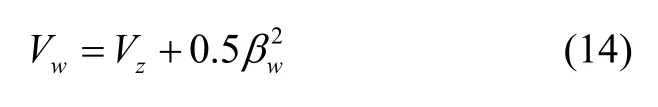
则式(14)关于时间的微分为：

由式(11)(12)可得：

进一步微分可得：

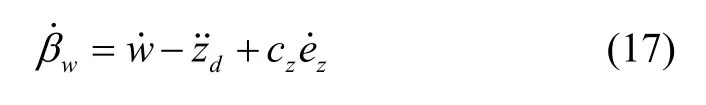
将式(17)带入式(15)得：

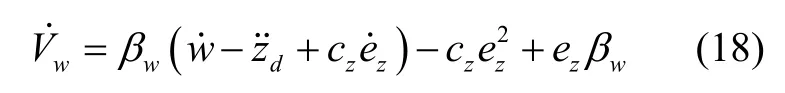
进一步化简为：

设定：

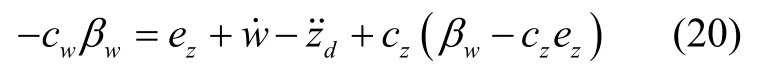
其中，cw为正常数，即cw＞ 0，则式(19)可表示为：

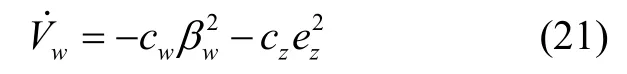
式(21)表明满足李雅普诺夫稳定性理论。

由式(20)可反推得到w微分为：

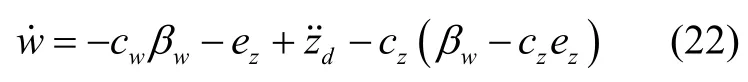
根据式(7)和式(22)可计算得到Z 通道虚拟控制变量U1为

由于dz为未知量，设定dz估计值换dz，则式(23)可表示为：

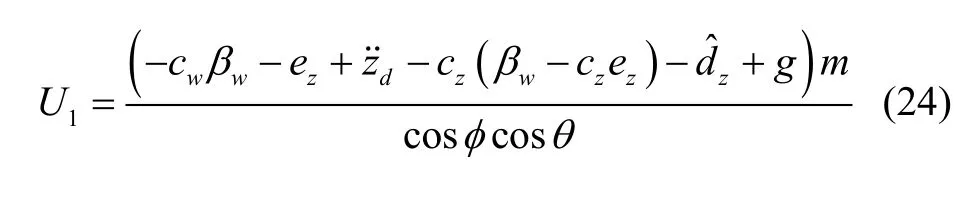
进一步，设计一个新的李雅普诺夫函数求取自适应控制律，

其中，λz为自适应因子，则式(25)的关于时间的微分可表示为：

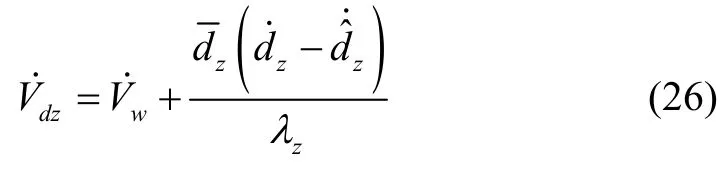
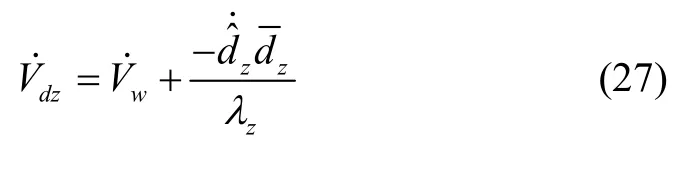
根据式(10)(20)(21)，式(27)可表示为

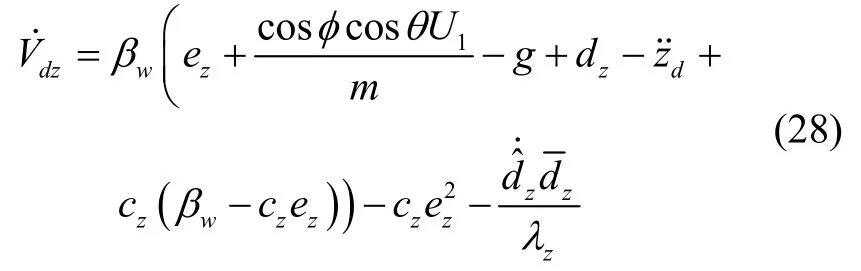
进一步化简为：

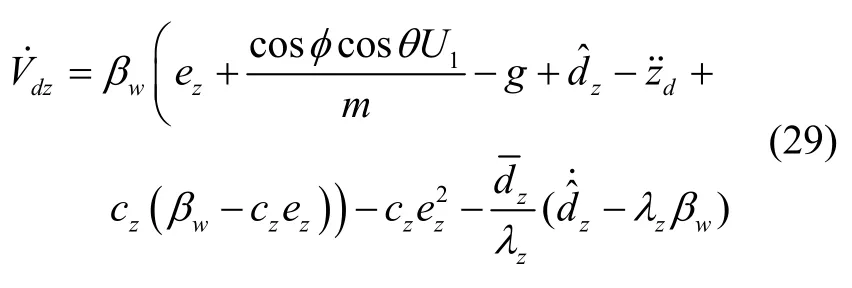
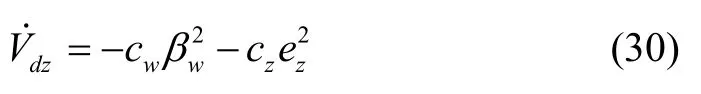
式(30)表明满足李雅普诺夫稳定性理论。

则Z 通道的虚拟控制变量可表示为：

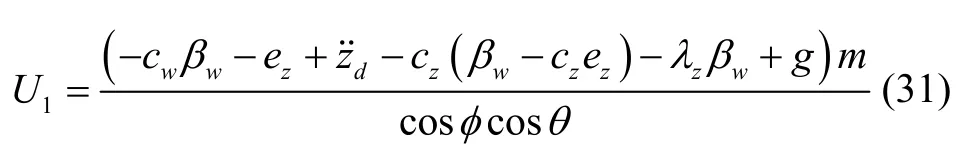
借鉴Z 通道设计方法，X 通道和Y 通道的虚拟控制变量可表示为：

其中，cu，cv，cx，cy，λx，λy为正常数；βu，βv分别表示X 轴速度分量u和Y 轴速度分量v的真实值与估计值的差值；分别为X 轴位置分量期望值和Y 轴位置分量期望值；ex，ey分别为X 轴位置分量x误差和Y 轴位置分量y误差。

2.2 姿态回路控制器设计

姿态回路与速度回路相互影响，稳定的姿态回路指令跟踪可保证位置回路的良好的轨迹跟踪效果，与位置回路相似，姿态回路同样采用自适应反步法实现姿态指令的准确跟踪，同时，在设计的自适应反步法的基础上，增加了积分项，减小姿态指令跟踪误差，提高四旋翼无人机飞行稳定性。

定义偏航角ψ跟踪误差为eψ=ψ-ψd，ψd为设定的期望偏航角，定义积分项为则关于偏航角ψ的李雅普诺夫函数可表示为：

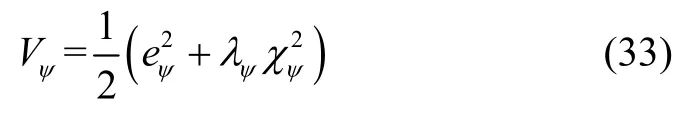
其中，λψ为正常数，即λψ＞ 0。

式(33)关于时间的微分为：

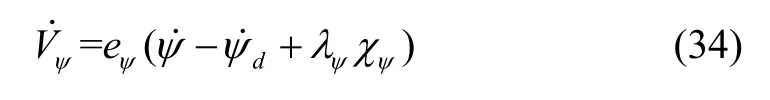
定义偏航角ψ跟踪误差关于时间的导数，估计值为αψ，则式(34)可表示为：

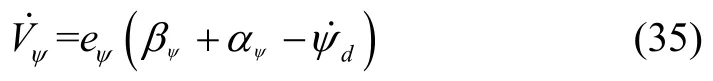
其中，

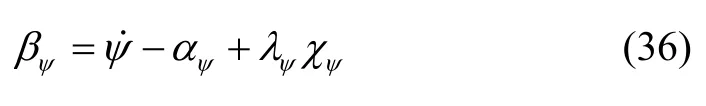
定义

其中，cψ为正常数，即cψ＞ 0。式(35)可简化为：

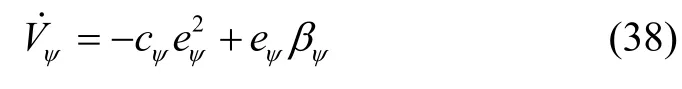
定义：

根据式(36)(37)可得：

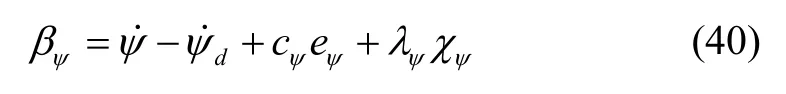
进一步化简可得：

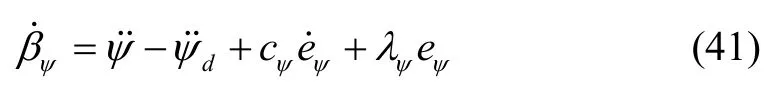
根据式(39)-(41)可得：

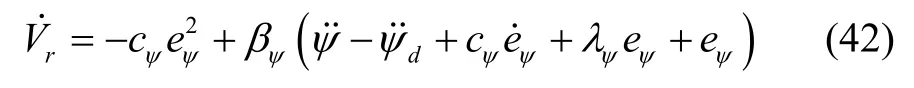
定义:

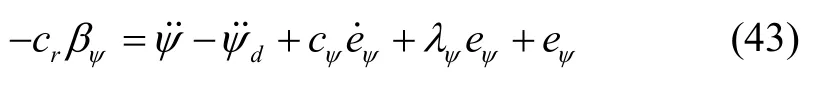
其中，cr为正常数，即cr＞ 0，则式(42)可表示为：

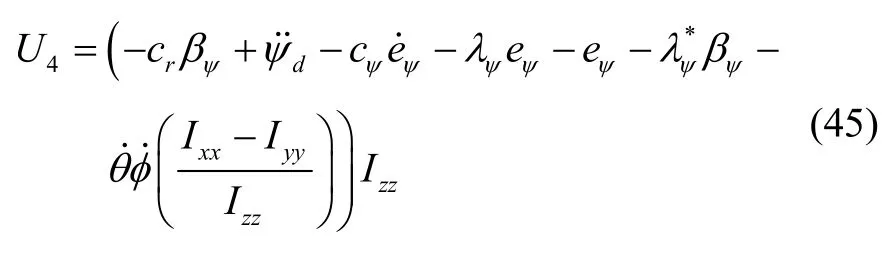
采用同样的设计方法设计滚转和俯仰通道得虚拟控制输入变量为：

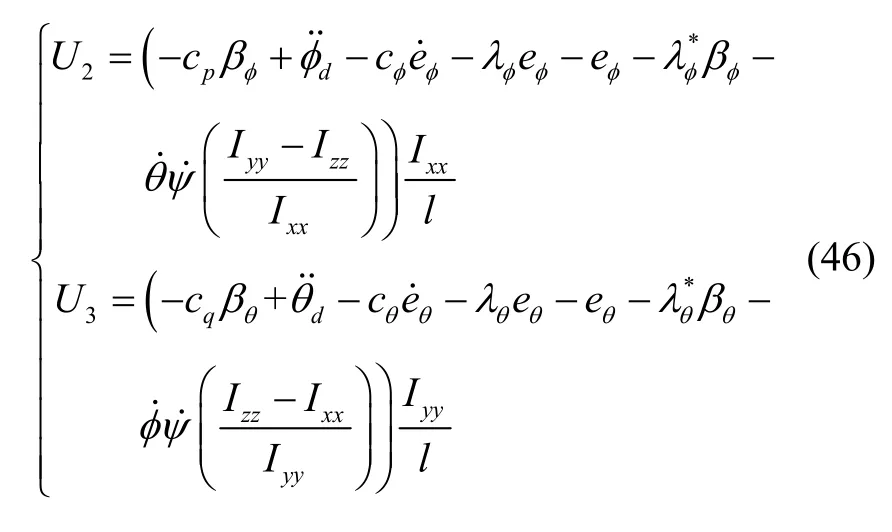
其中，cp，cq，cφ，cθ，λφ，λθ，均为正常数；φd和θd分别为期望滚转角和期望俯仰角；eφ，eφ分别为滚转角和俯仰角跟踪误差；βφ和βθ为

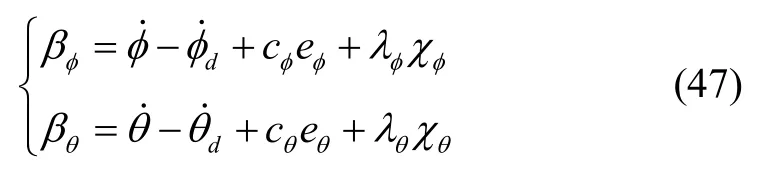
3 仿真实验与分析

为验证本文设计的自适应积分反步法抗干扰能力，这里选取已建立的四旋翼动力学模型为研究对象，并分别在不同频率和不同强度随机干扰影响下测试无人机指令跟踪精度和跟踪误差修正能力。其中四旋翼动力学模型的关键参数如表2 所示。

表2 四旋翼动力学模型参数及初始化参数Tab.2 The model parameters and initialization parameters

其中，x0，y0，z0为四旋翼初始位置状态量；u0，v0，w0为四旋翼初始速度变量；φ0，θ0，ψ0为四旋翼初始姿态角；p0，q0，r0为初始姿态角速度。

设定四旋翼位置回路控制参数为：cx= 7，cy= 7，cz=6.6，cu=1.38，cv=1.38，cw= 1.4，λx= 4.6，λy= 4.6，λz= 4.6；姿态回路自适应积分反步法控制参数为：λφ= 0.1，λθ= 0.1，λψ=0.05，cφ= 3，cθ=3，cψ=5，cp=17，cq=17，cr=30，。

仿真1：设定四旋翼受强度为6 m/s2，频率为1 Hz 的随机干扰影响，验证自适应积分反步法双回路控制系统在外界干扰下准确跟踪控制指令的能力。仿真结果如图3-7 所示。

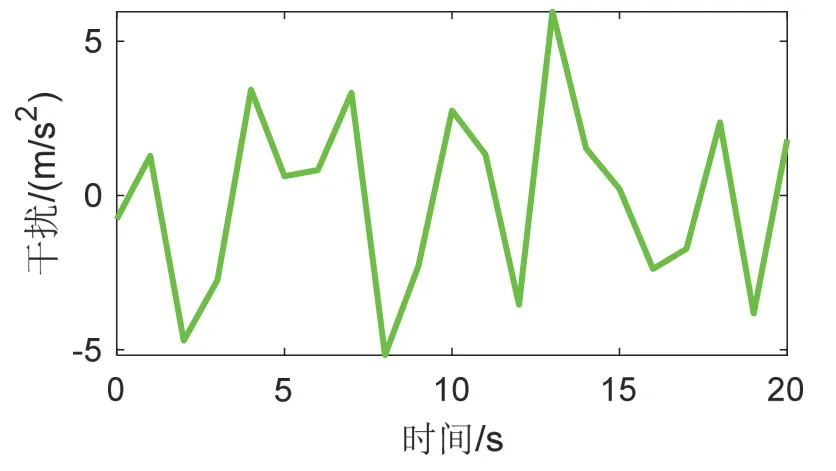
图3 四旋翼随机干扰变化曲线Fig.3 The disturbance of quadrotor

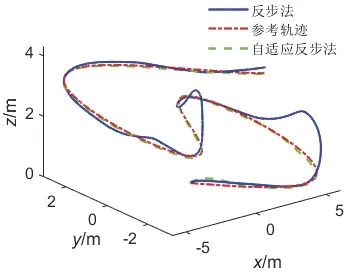
图4 四旋翼指令跟踪轨迹曲线Fig.4 The path of trajectory tracking

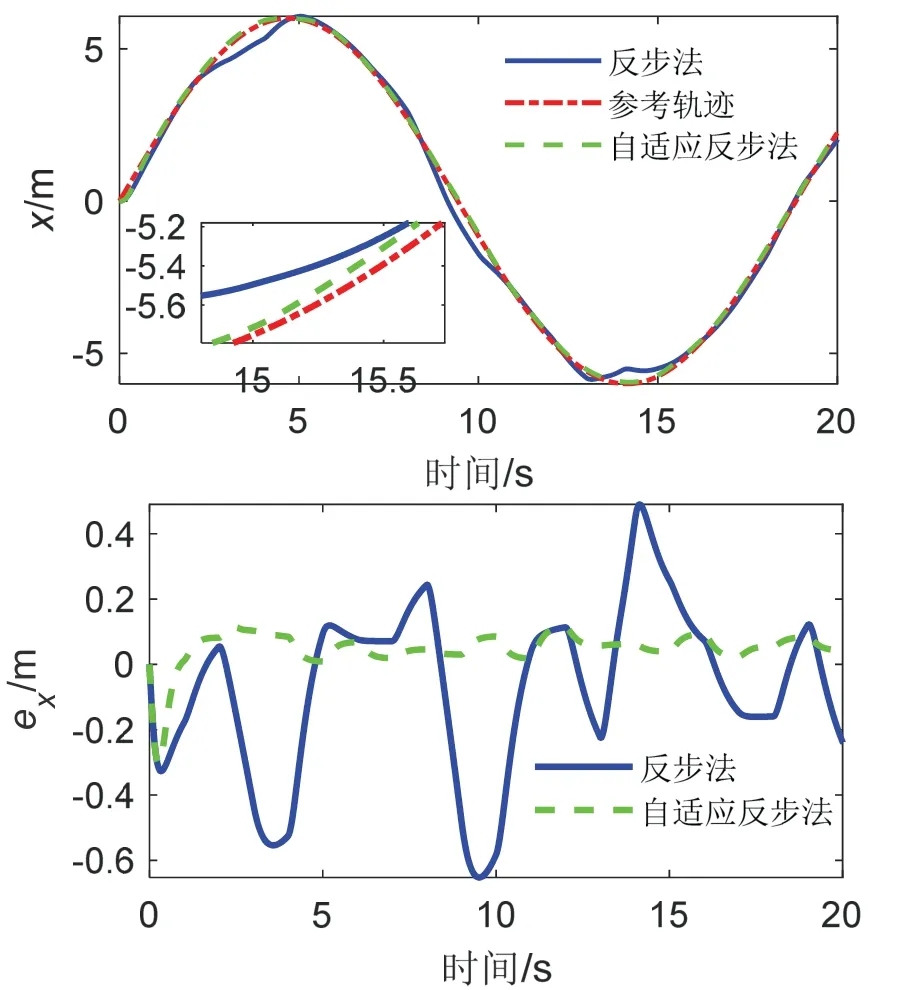
图5 X 通道指令跟踪及误差曲线Fig.5 The responses of trajectory tracking of X channel

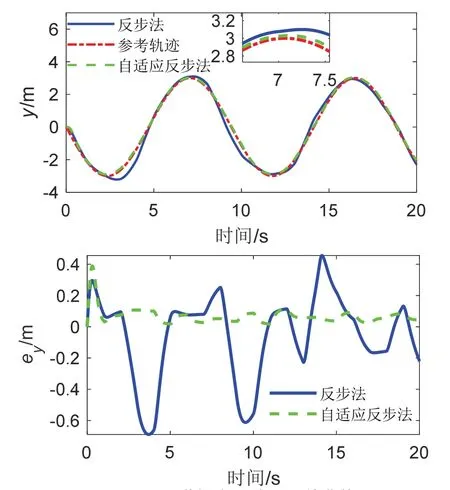
图6 Y 通道指令跟踪及误差曲线Fig.6 The responses of trajectory tracking of Y channel

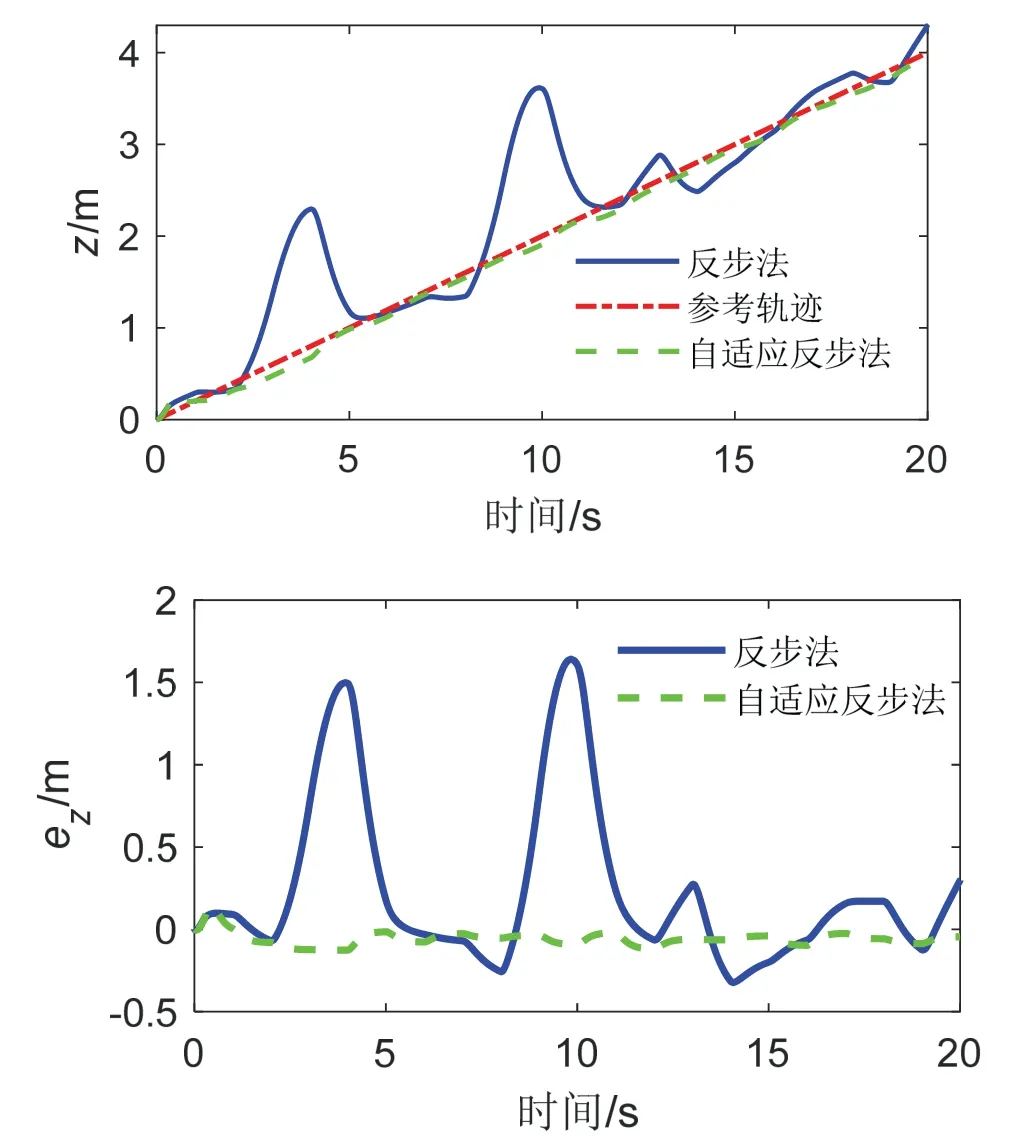
图7 Z 通道指令跟踪及误差曲线Fig.7 The responses of trajectory tracking of Z channel

其中，图3 为轨迹跟踪过程中受到的随机干扰曲线变化图；图4 为四旋翼无人机轨迹三维变化曲线；图5、图6 和图7 中的上图分别为X 通道、Y 通道和Z 通道的轨迹跟踪曲线；图5、图6 和图7 中的下图为对应的轨迹跟踪误差曲线。图4-7 中红色线条为参考轨迹，蓝色为基于传统反步法的指令跟踪曲线，绿色为基于自适应积分反步法的指令跟踪曲线。

由图4 以及图5、图6 和图7 中的上图可看出，蓝色曲线存在多处震荡偏离参考轨迹的现象，特别是图7 上图中的Z 通道轨迹变化曲线震荡严重偏离了红色曲线，而绿色曲线变化较为平滑，无剧烈震荡现象，且更加接近于参考轨迹。图5、图6 和图7 中的下图反映了X、Y、Z 通道对应的轨迹跟踪误差曲线，可明显看出，绿色曲线振幅较小，ex、ey、ez在整个仿真周期中最大峰值仅为-0.30 m、0.39 m、-0.14 m，而蓝色曲线最大峰值可达到-0.65 m、-0.69 m、1.64 m。表明在低频率、高强度干扰影响下，基于自适应积分反步法控制器能更好地估计并补偿干扰误差，表现效果更好。

仿真2：设定四旋翼受强度为62m/s ，频率为5 Hz 的随机干扰影响，验证自适应积分反步法双回路控制系统在外界干扰下准确跟踪控制指令的能力。仿真结果如图8-12 所示。

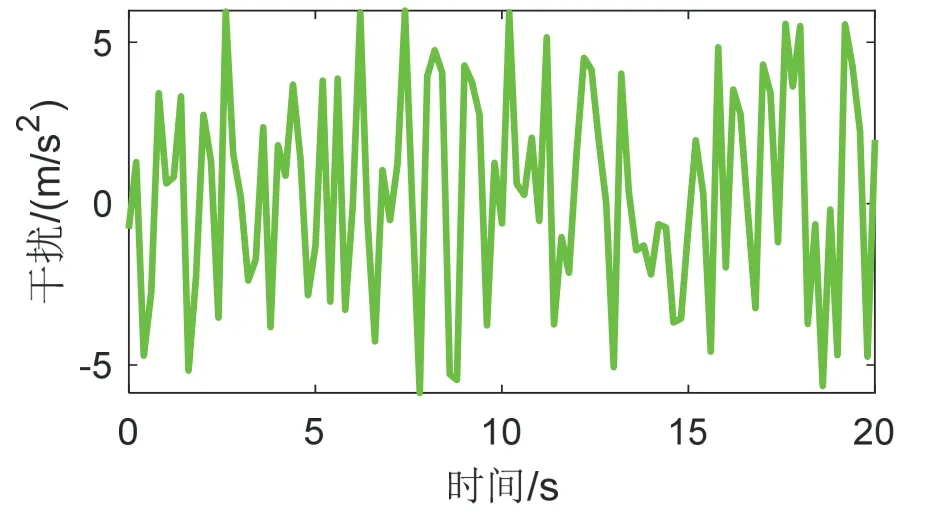
图8 四旋翼随机干扰变化曲线Fig.8 The disturbance of quadrotor

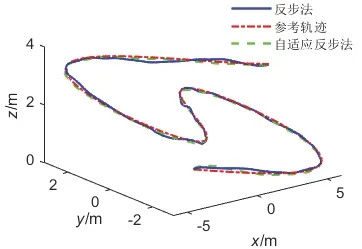
图9 四旋翼指令跟踪轨迹变化曲线Fig.9 The path of trajectory tracking

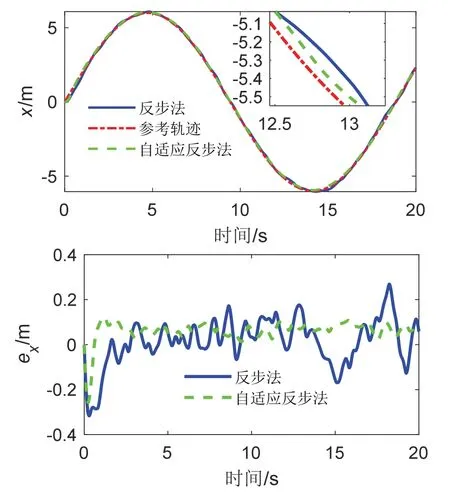
图10 X 通道指令跟踪及误差曲线Fig.10 The responses of trajectory tracking of X channel

其中，图8 为轨迹跟踪过程中受到的随机干扰曲线变化图；图9 为四旋翼轨迹三维变化曲线；图10、图11 和图12 中的上图分别为X 通道、Y 通道和Z 通道的轨迹跟踪曲线；图10、图11 和图12 中的下图为对应的轨迹跟踪误差曲线。图9-12 中红色线条为参考轨迹，蓝色为基于传统反步法的指令跟踪曲线，绿色为基于自适应积分反步法的指令跟踪曲线。

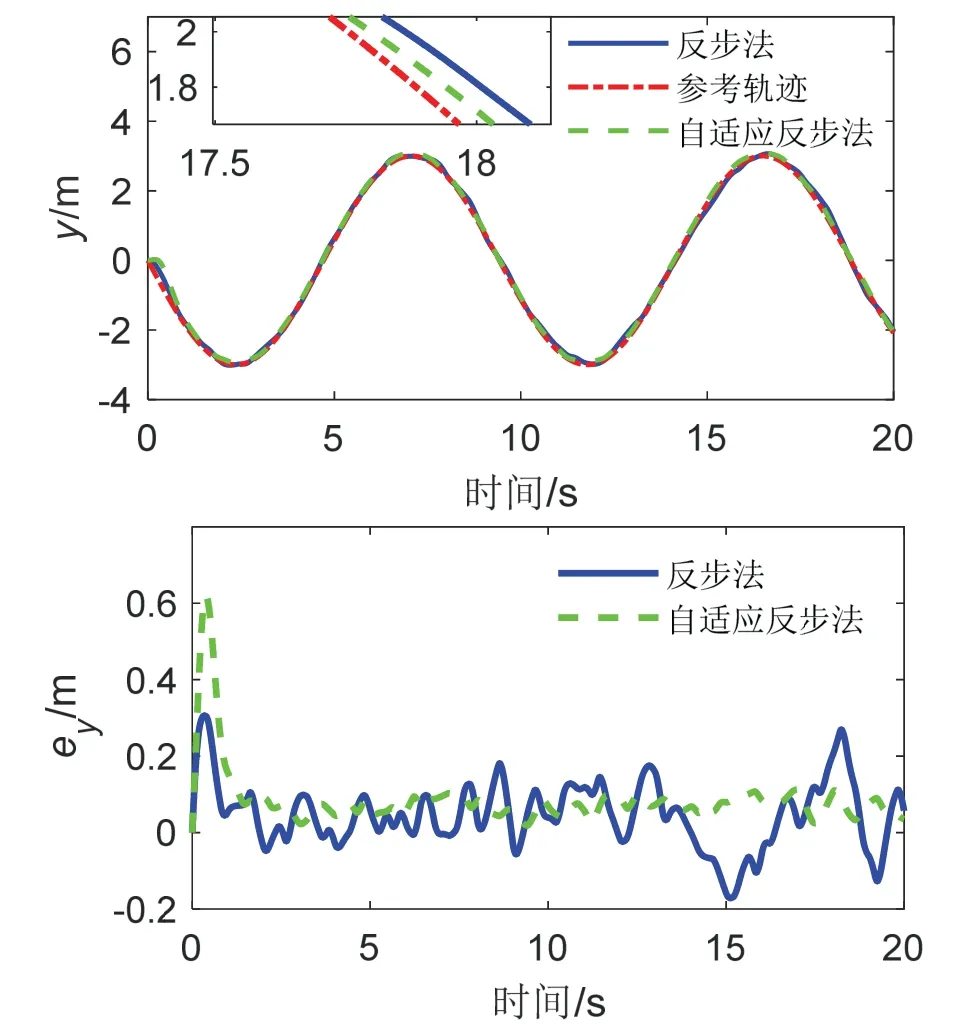
图11 Y 通道指令跟踪及误差曲线Fig.11 The responses of trajectory tracking of Y channel

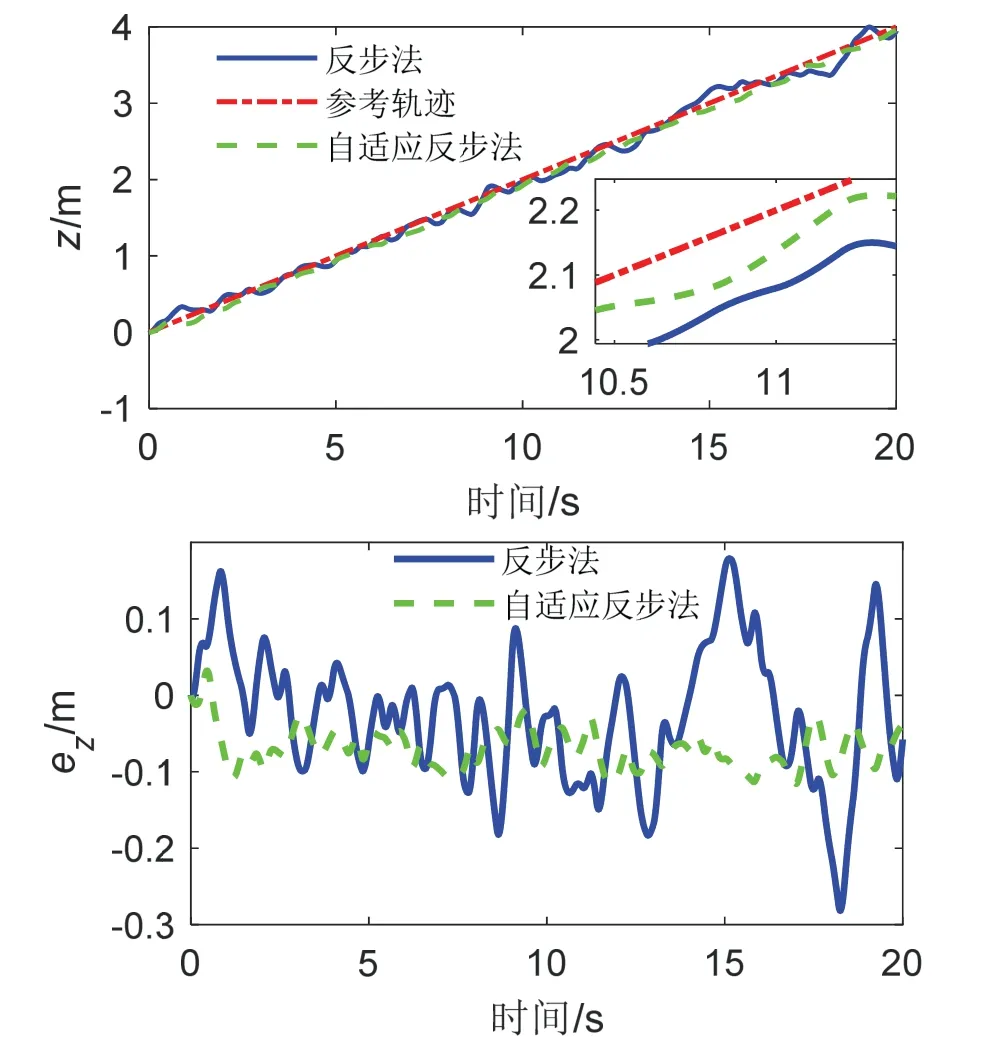
图12 Z 通道指令跟踪及误差曲线Fig.12 The responses of trajectory tracking of Z channel

由图9 以及图10-12 中的上图可看出，蓝色曲线存在多处震荡偏离参考轨迹的现象，特别是图12 的上图中的Z 通道轨迹变化曲线震荡严重偏离了红色曲线，且通过对比图5-7 中的上图可知，四旋翼在同强度高频干扰信号下跟踪表现更好，实际飞行轨迹更加靠近参考轨迹，但无人机轨迹震荡加剧，特别是在基于传统反步法控制器下，无人机震荡频率更加频繁，无人机稳定性能表现更差。而图9 以及图10-12 的上图中绿色曲线变化较为平滑，无剧烈震荡现象，且更加接近于参考轨迹。图10-12 中的下图反映了X、Y、Z 通道对应的轨迹跟踪误差曲线，可明显看出，除初始阶段绿色曲线出现较大峰外，后期轨迹跟踪过程中基于自适应积分反步法的四旋翼轨迹跟踪误差振幅明显较小，而蓝色曲线在整个飞行过程中均剧烈震荡，且存在后期跟踪过程中震荡加剧现象，进一步表明四旋翼在高频率、高强度干扰影响下，基于自适应积分反步法控制器能够更快响应干扰，并自适应调整补偿值，使得后期轨迹跟踪效果明显优于基于传统反步法的轨迹跟踪效果。

仿真3：设定四旋翼受强度为12m/s ，频率为1 Hz 的随机干扰影响，验证自适应积分反步法双回路控制系统在外界干扰下准确跟踪控制指令的能力。仿真结果如图13-17 所示。

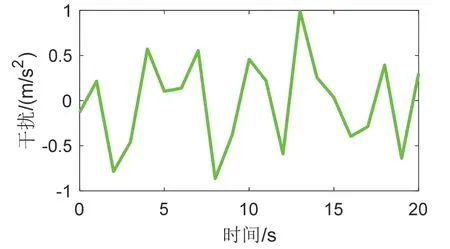
图13 四旋翼随机干扰变化曲线Fig.13 The disturbance of quadrotor

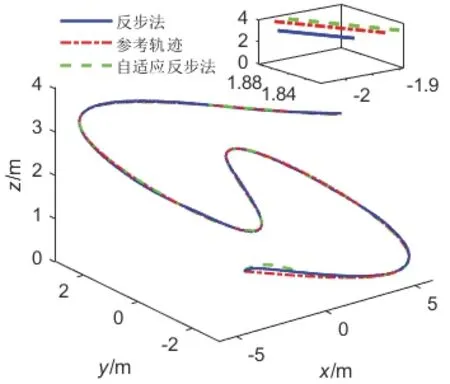
图14 四旋翼指令跟踪轨迹曲线Fig.14 The path of trajectory tracking

其中，图13 为轨迹跟踪过程中受到的随机干扰曲线变化图；图14 为四旋翼轨迹三维变化曲线；图15-17 中的上图分别为X 通道、Y 通道和Z 通道的轨迹跟踪曲线；图15-17 中的下图为对应的轨迹跟踪误差曲线。图13-17 中红色线条为参考轨迹，蓝色为基于传统反步法的指令跟踪曲线，绿色为基于自适应积分反步法的指令跟踪曲线。

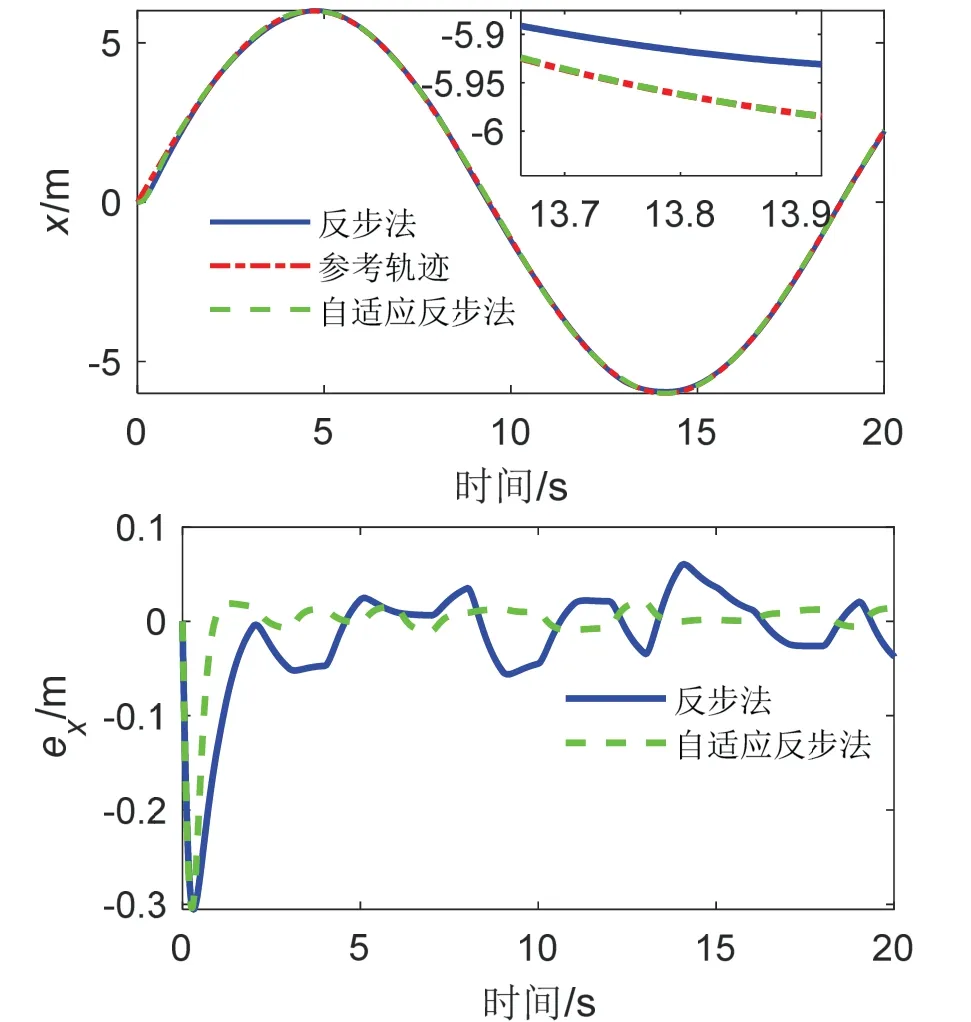
图15 X 通道指令跟踪及误差曲线Fig.15 The responses of trajectory tracking of X channel

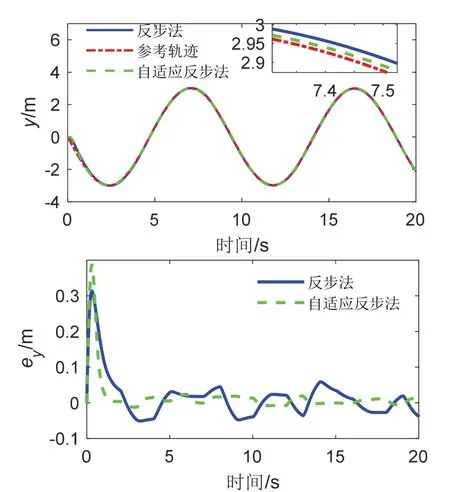
图16 Y 通道指令跟踪及误差曲线Fig.16 The responses of trajectory tracking of Y channel

由图14 以及图15-17 中的上图可看出，在低频、低强度随机干扰影响下，基于自适应反步法与基于传统反步法的轨迹跟踪均表现良好，进一步说明该类型干扰对无人机实际飞行造成的影响可忽略不计，但图中小图仍可看出，绿色曲线较蓝色曲线更加接近于参考轨迹。由图15-17 的下图可知，虽基于自适应积分反步法的轨迹跟踪误差在初始阶段误差较大，但第一个峰值过后跟踪误差明显减小，且能够稳定保持在较小的范围内震荡；而基于传统反步法的轨迹跟踪误差在全程均表现出大幅度震荡现象。分析表明自适应积分反步法在低强度、低频率干扰下同样表现出更加优秀的跟踪效果。

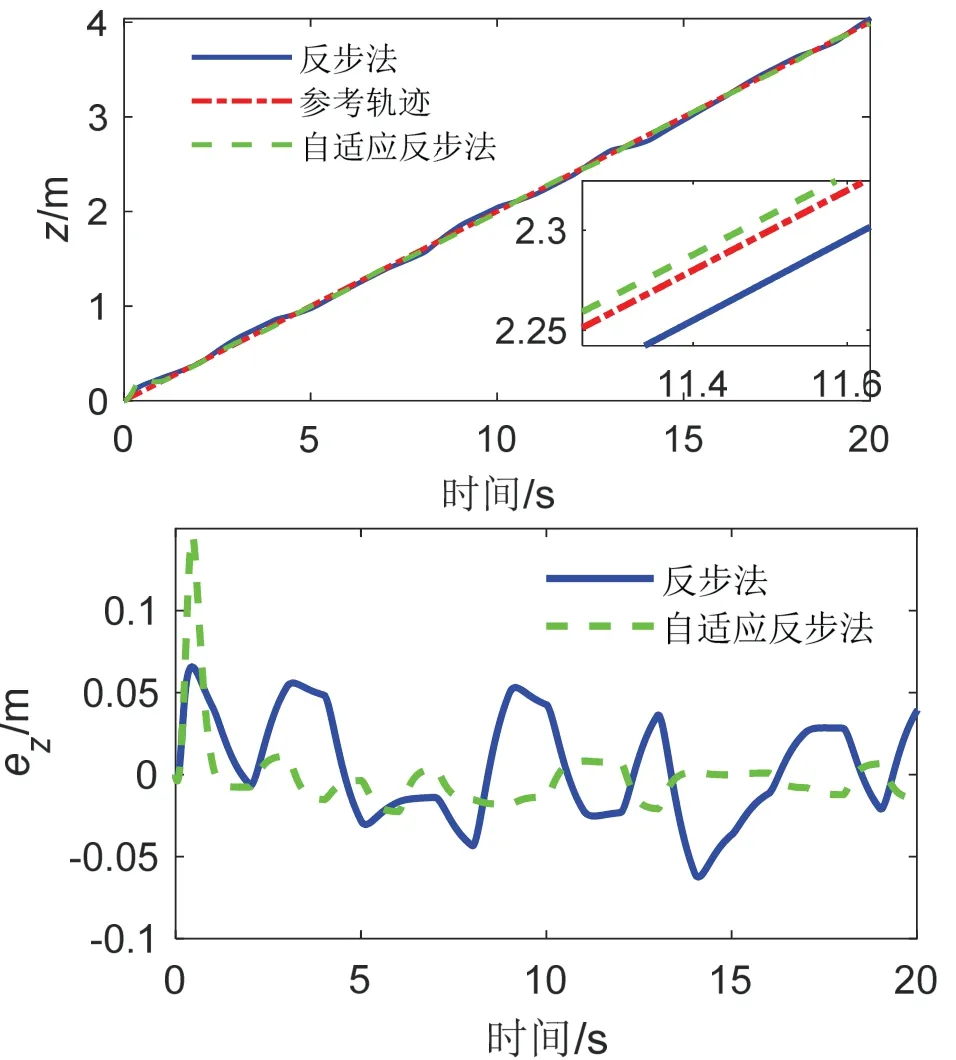
图17 Z 通道指令跟踪及误差曲线Fig.17 The responses of trajectory tracking of Z channel

通过对比仿真1 与仿真2 测试效果可知，同强度下，低频干扰对无人机飞行影响更大；对比仿真1 与仿真3 测试效果可知，同频率下，高强度干扰对无人机更容易造成无人机失稳现象。在低频高强度干扰下，自适应反步法轨迹跟踪精度分别为0.30 m、0.39 m、0.14 m，传统反步法跟踪精度分别为0.65 m、0.69 m、1.64 m，跟踪精度提高4.2 倍。且在轨迹跟踪后期，自适应积分反步法跟踪误差进一步减小，三通道分别表现为0.1125 m、0.1109 m、0.1182 m，稳定性提高13 倍。进一步表明本文设计的自适应积分反步法抗干扰控制器在各类干扰环境影响下具有更好的稳定性。

4 结 论

本文提出了一种基于自适应积分反步法的无人机轨迹跟踪控制策略，有效解决了四旋翼无人机因外界干扰及自身不确定性因素造成的轨迹跟踪误差大，难以控制的问题，提高了无人机的轨迹跟踪精度与速度，并保证了无人机良好的鲁棒性和稳定性。其中，在位置回路中加入了自适应因子补偿不确定性干扰误差，提高轨迹跟踪的精度，在速度回路中分别加入了自适应因子和指令跟踪误差积分项，在弱化误差影响的同时保证了无人机良好的稳定性。最后通过不同强度、不同频率下抗干扰测试，证明了自适应积分反步法抗干扰控制器的有效性与可行性。

本文提出的自适应积分反步法虽已在Simulink 环境下仿真验证了其具有更好的抗干扰性能，但由于精力有限，未完成实物飞行测试，后续研究将从无人机实际飞行抗干扰测试方面进一步深入研究，论证本文提出的自适应积分反步法的工程适用性。