超像素驱动的代理辅助多目标聚类图像分割
赵 凤,张莉阳
(西安邮电大学 通信与信息工程学院,陕西 西安 710121;西安邮电大学 电子信息现场勘验应用技术公安部重点实验室,陕西 西安 710121)
图像分割是指将图像分成若干互不重叠的子区域,使得同一个子区域内的特征具有一定相似性、不同子区域间特征呈现较为明显的差异[1]。现有的图像分割方法主要包括阈值的方法[2]、区域的方法[3]和聚类的方法[4]等。其中,基于聚类的方法是众多研究者研究的热点之一,模糊C-均值(fuzzy C-means,FCM)聚类算法[5]是一种经典的聚类算法,但是FCM算法具有对聚类中心初始值敏感、易陷入局部最优及易受噪声影响等缺点。针对FCM算法的不足,核模糊C-均值聚类算法[6](kernel fuzzy C-means clustering,KFCM)将原空间线性不可分的样本变为线性可分或近似线性可分。
在实际应用中,为了满足不同需求,需要从多个角度考虑问题。因此,多目标进化算法(multi-objective evolutionary genetic algorithm,MOEA)的研究吸引到众多研究者的关注,多目标进化聚类算法也取得了丰硕的成果[7]。与单目标聚类算法相比,多目标进化聚类算法降低了对聚类中心初始值的敏感程度且解决了易陷入局部最优的缺点。此外,该类算法通过选取合适的染色体编码策略和适应度函数可以自动确定聚类数目,减少了人为干预。多目标可变长遗传模糊聚类算法[8](multi-objective variable string length genetic fuzzy clustering algorithm,MOVGA)已经被成功应用于脑部医学图像的分割。
然而,多目标进化聚类算法应用于图像分割时,往往是基于像素进行聚类,分割效果不好且运行时间太长。为此,通过引入超像素信息和基于代理辅助参考向量引导的多目标进化算法,拟提出一种超像素驱动的代理辅助多目标聚类图像分割算法。利用超像素策略得到超像素区域,并提取每个超像素区域的代表特征得到超像素信息,采用融合超像素信息的MOVGA有效性函数作为适应度函数,进行基于代理辅助参考向量引导的多目标进化聚类,并采用融合超像素信息的最优解评价指标选取最优解,实现多目标进化聚类图像分割。
1 多目标进化聚类算法
1.1 多目标优化理论
在人们的日常生活和工作中,经常会遇到需要优化多个相互冲突的目标问题,这类问题被称为多目标优化问题。以最小化目标函数为例,假设决策变量为z=(z1,z2,…,zα),目标函数为f(z)=[f1(z),f2(z),…,fβ(z)],那么多目标优化问题的数学表达式为
其中,满足约束条件gi(z)和hj(z)的变量z为可行解,所有可行解的集合称为可行解集合。设z1和z2是上述最小化多目标优化问题的两个可行解,当且仅当对所有子目标函数,z1不比z2差,且至少存在一个子目标函数,z1比z2好,则称z1Pareto支配z2。一个解被称为Pareto最优解或者非支配解,当且仅当没有其他解可以支配它。由Pareto最优解构成的集合被称为Pareto最优解集或者非支配解集。
1.2 多目标进化聚类
进化算法是一种全局优化算法。将进化算法引入到多目标优化中,使得聚类算法具有较强的全局搜索能力。不同的多目标进化优化算法相继被提出,如非支配排序遗传算法[9](non-dominated sorting genetic algorithm,NSGA)和改进的非支配排序遗传算法NSGA-II[10]等。
多目标进化聚类算法[11]利用多目标进化算法同时优化反映连通性和总体偏差的两个适应度函数,但是,该算法属于硬聚类,不符合现实世界亦此亦彼的特点。MOVGA算法可同时优化类内紧致和类间分离两个适应度函数实现多目标进化聚类[8]。现有的多目标进化聚类算法通常是采用NSGA-II算法作为基本大框架。
2 超像素驱动代理辅助多目标聚类
2.1 超像素区域代表特征的获取
传统的聚类算法应用于图像分割时,通常是基于像素进行聚类,分割效果不好,且计算效率很低。2003年,超像素[12]的概念被提出。所谓超像素,是指图像中局部的、具有一致性的,能够保持一定图像局部结构特征的子区域[13]。之后,学者们提出了众多超像素算法,如Normalized cuts算法[14]和简单线性迭代聚类[15](simple linear iterative cluster,SLIC)算法等。
然而,超像素算法计算复杂度较高,边缘分割贴合度较差。差分进化超像素分割[16-17](differen-tial evolutionary superpixel segmentation,DES)算法与其他超像素算法相比,最大的优点是在对图像进行超像素分割时,考虑多个全局属性的综合目标函数,包括超像素内误差、边界梯度和正则化项,然后在差分进化这个强大的全局优化器上完成优化,超像素边缘贴合度更高,形状更加规则,且该算法的计算复杂度与图像大小成正比。因此,超像素驱动的代理辅助多目标聚类图像分割算法采用DES方法提取图像的超像素区域。
对图像进行差分进化超像素分割,获得K个超像素区域B={B1,B2,…,BK},然后提取每个超像素区域的代表特征。对于第k个超像素区域,其代表特征红绿蓝(red green blue,RGB)值[18]的计算公式为
其中:yp表示该超像素区域内像素点p的RGB特征值;yn表示该超像素区域内中值像素点n的RGB特征值。w(yp,yn)表示像素点p与n之间的权重,计算公式为
w(yp,yn)=Dpn×Lpn,
Lpn=e-|yp-yn|2/δ2。
其中:(ρ,θ)表示超像素中像素点的坐标;x表示超像素中像素点的个数;δ表示该超像素区域的颜色特征方差。Dpn表示位置权重[19],像素点p距离n越近,其权重越高。Lpn表示颜色权重[18],像素点p与n颜色信息越接近,其权重越高。最后得到超像素区域的代表特征r={r1,r2,…,rK}。
2.2 适应度函数计算
在多目标进化聚类算法中,通常根据适应度函数的大小对个体进行优胜劣汰,选择合适的适应度函数对提高算法性能很关键。因此,所提算法采用两个适应度函数,一个是融合超像素信息的类内紧致性函数,另一个是融合超像素信息的类间分离性函数。融合超像素信息的类内紧致性函数定义为
(1)
其中:m表示模糊指数;C表示聚类数目;vi表示第i类聚类中心;uik表示第k个超像素区域对第i类聚类中心的隶属度,计算公式为
(2)
融合超像素信息的类间分离性函数定义为
(3)
其中,μlq表示vq相对于vl的隶属度,计算公式为
根据函数J和S的描述可知,J要尽可能小,S要尽可能大。
2.3 染色体编码、种群初始化及进化操作策略
对聚类中心采用实数编码。假设一个染色体是由d维数据空间里的C个聚类中心组成,那么该染色体的长度为d×C。例如,在三维数据空间里,两个聚类中心(19.9,15.5,17.4)和(129.9,132.8,48.9)构成染色体(19.9,15.5,17.4,129.9,132.8,48.9)。所提算法的初始种群是从超像素区域的代表特征r={r1,r2,…,rK}中随机选取产生。
采用基于代理辅助参考向量引导的多目标进化算法[20](kriging-assisted reference vector guided evolutionary algorithm,K-RVEA)进行多目标聚类图像分割。Kriging模型[21]作为代理模型,以基于参考向量引导的进化算法[22](reference vector guided evolutionary algorithm,RVEA)为底层进化算法。K-RVEA首先初始化一组均匀分布的参考向量[22],使用这组参考向量将目标空间划分为多个子空间,并使用参考向量在每个子空间中指导选择新个体;然后利用初始种群中的所有个体对于每个适应度函数训练Kriging模型,通过模拟二进制交叉算子和多项式变异算子生成子代种群,利用Kriging模型预测子代个体的适应度函数值。采用基于角度惩罚距离的选择策略[22]选择新种群。在管理Kriging模型时,利用Kriging模型给出近似目标值中的不确定性信息、参考向量的分布以及个体的位置,既保证了多样性和收敛性,又保证了二者的平衡,在多目标进化优化问题中至关重要。
2.4 最优解的选取
在进化到最后一代时,会得到一个非支配解集,每一个解都同等重要,但是,实际应用中通常只需要一个最优解。聚类有效性指数I[23]通常被用来作为多目标进化的选解指标,从非支配解集中选择使I值最大的解作为最优解。所提算法将超像素信息引入I指标,构造融合超像素信息的有效性指数SI从非支配解集中选择出一个最优解,其定义式为
(4)
(5)
(6)
其中:E1对于给定的数据集来说是一个常数。EC度量了类内紧致性,其值越小越好;DC度量了两个类之间的最大可分性,其值越大越好。因此,SI值越大越好。
2.5 算法流程
所提算法步骤具体如下。
步骤1对彩色图像进行差分进化超像素分割,得到K个超像素区域,提取每个超像素区域的代表特征r={r1,r2,…,rK}。
步骤2设置种群规模N,最大迭代次数T,聚类数目C,用于更新Kriging模型的个体数目M,更新Kriging模型之前的固定迭代次数wmax,交叉概率p0和变异概率pm。
步骤3初始化参考向量、染色体编码和初始化种群。
步骤4按照式(1)和式(3)计算初始种群的适应度函数值,并使用初始种群中的个体及其适应度函数训练Kriging模型,设置t=0,w=0。
步骤5利用进化操作策略生成子代种群,利用Kriging模型预测目标函数值,并将父代与子代合并。
步骤6采用基于角度惩罚距离的选择策略选择新种群,更新参考矢量,并设置w=w+1。
步骤7判断是否需要更新Kriging模型。若w>wmax,则更新Kriging模型,并设置w=0,执行步骤8;若否,直接执行步骤8。
步骤8判断是否达到最大迭代次数,若是,则迭代终止,得到最后一代非支配解集;否则,t=t+1,执行步骤5。
步骤9利用式(4)选出最优个体,得到最优的聚类中心。
步骤10根据最优聚类中心,对每个超像素区域进行标签分配进而获得图像中所有像素的标签,输出图像分割结果。
3 实验结果与分析
3.1 实验设置及说明
为了验证所提算法的分割性能,采用多幅Berkeley图像[24]和Weizmann图像[25]进行实验。以K-RVEA为进化策略,以MOVGA的两个目标函数为适应度函数,构造KRVEA-MOVGA。分别对比FCM算法[5]、KFCM算法[6]、MOVGA[8]、KRVEA-MOVGA和所提算法的分割准确率。实验均在CPU为Intel(R) Core(TM) i5-6 500,内存为8 GB,系统类型为64位操作系统配置的台式机上运行,使用仿真软件为Matlab 2018a。
所有算法的模糊指数均设置为2;最大迭代次数均设置为100;FCM算法、KFCM算法、KRVEA-MOVGA及所提算法的聚类数目均是根据人工分割的标准图提前给定,MOVGA的聚类数目自适应确定,其最大值设置为10;FCM算法和KFCM算法的结束阈值设置为10-5;MOVGA、KRVEA-MOVGA及所提算法的种群规模均设置为50,交叉概率设置为0.9,变异概率设置为0.1;所提算法的超像素数目设置为500。
3.2 Berkeley图像分割实验
5种算法在12幅Berkeley图像上的分割准确率如表1所示。可以看出,所提算法在大多数情况下,相较于其他4种算法能取得更好的分割结果。例如,对于图像#3063,所提算法的图像分割准确率达到0.993 8,比FCM算法、KFCM算法、MOVGA和KRVEA-MOVGA分别提高了0.264 7、0.433 0、0.346 1和0.001 0。
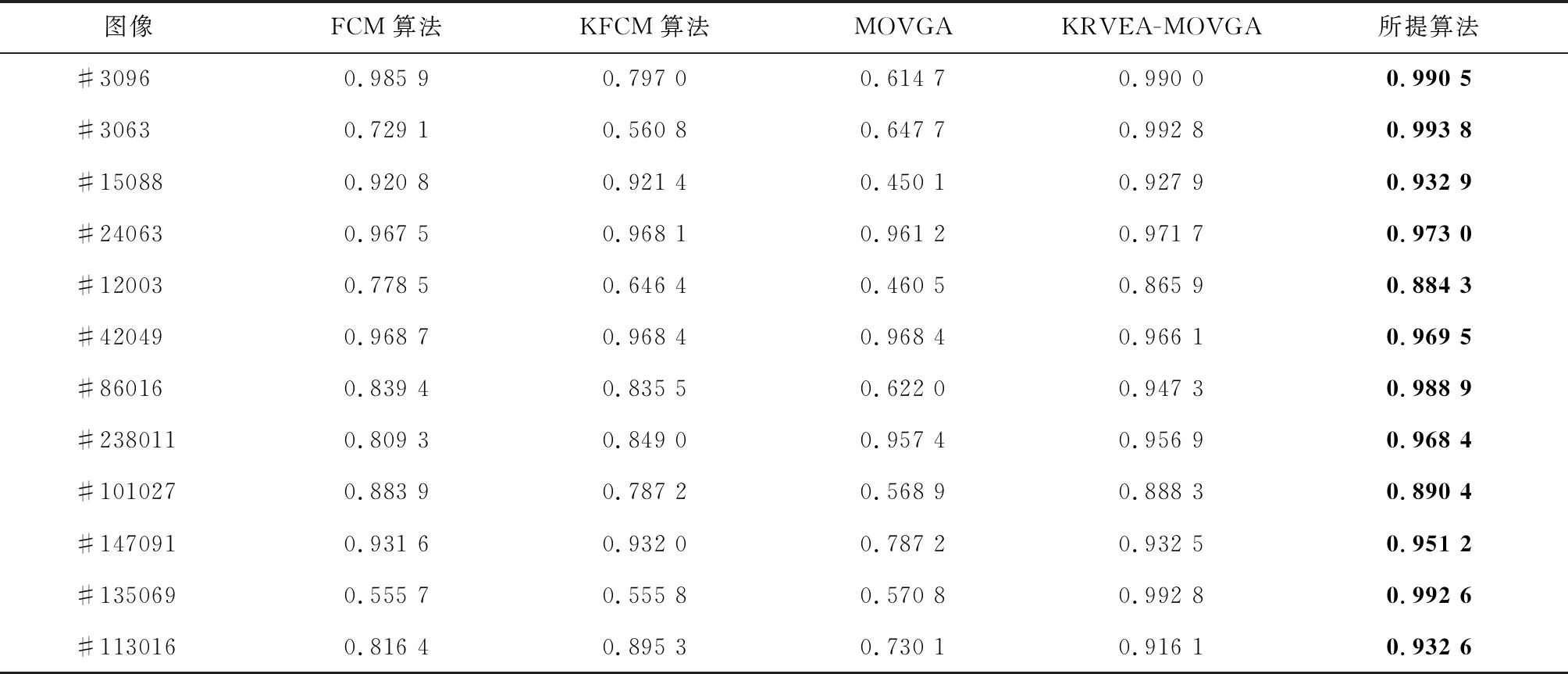
表1 5种算法对Berkeley图像的分割准确率
MOVGA、KRVEA-MOVGA和所提算法在12幅Berkeley图像平均运行时间分别为628 s、46 s和32 s,因此,与其他多目标进化聚类算法相比,所提算法不仅提高了图像分割效果,同时也提高了时间效率。
为了检验所提算法在Berkeley图像的视觉分割效果,图1-图3分别给出了图像#3063、#24063和#238011在所有算法上的分割结果。从图1中可以看出,FCM算法和KFCM算法的结果有较多错分,MOVGA的结果中,天空背景分割效果不好,而所提算法相较于KRVEA-MOVGA,分割效果更好。从图3中可以看出, FCM算法和KFCM算法都有错分,所提算法相较于其他算法,展示出了更好的分割效果。
3.3 Weizmann图像分割实验
5种算法在12幅Weizmann图像上的分割准确率如表2所示。可以看出,所提算法在大多数图像上的分割性能是所有算法中最好的。例如,对于图像#leafpav,所提算法的图像分割准确率达到0.987 5,比FCM算法、KFCM算法、MOVGA和KRVEA-MOVGA的准确率分别提高了0.015、0.012 4、0.452 4和0.004 5。

表2 5种算法对Weizmann图像的分割准确率

续表2 5种算法对Weizmann图像的分割准确率
MOVGA、MOVGA和所提算法在12幅Weizmann图像平均运行时间分别为301 s、36 s和32 s,因此,与其他多目标进化聚类算法相比,所提算法不仅提高了图像分割效果,同时也提高了时间效率。
为了检验所提算法在Weizmann图像的视觉分割效果,图4和图5分别给出了图像europe_holiday_484和beltaine_4_bg_050502在所有算法上的分割结果。从图5可以看出,FCM算法、KFCM算法和MOVGA的结果有较多错分,没有将背景与目标分离,与KRVEA-MOVGA相比,所提算法的图像分割效果更好。
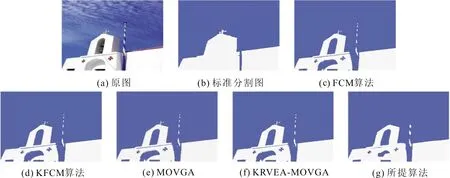
图4 europe_holiday_484分割结果

图5 beltaine_4_bg_050502分割结果
4 结语
超像素驱动的代理辅助多目标聚类图像分割算法先对彩色图像进行超像素分割得到超像素区域,然后提取每个超像素区域的代表特征。设计融合超像素信息的适应度函数和最优解评价指标,基于代理辅助参考向量引导进行多目标进化聚类。实验结果表明,相比于FCM算法、KFCM算法、MOVGA和KRVEA-MOVGA,该算法能够取得较好的图像分割结果,同时也提高了时间效率。

