利率水平对中国上市商业银行违约概率的影响
——基于贝叶斯向量自回归实证分析
刘志洋
(东北师范大学 经济与管理学院,吉林 长春 130117)
一、引言
自从1996年巴塞尔委员会发布市场风险管理资本计提要求之后,各国金融监管当局开始关注市场风险对银行体系风险的影响。根据巴塞尔资本协议,市场风险主要包括利率风险、汇率风险、股价风险和商品价格风险。对于商业银行来讲,利率风险无疑是影响最大的系统风险因子。随着中国利率市场进程基本完成,利率水平的高低直接影响着实体经济的增长,进而影响银行业的稳定。当利率水平较高时,商业银行持有的债券价值就会降低,且实体企业的信用风险也会上升,这些都会给商业银行资产负债管理带来压力。虽然中国尚未发生“黑天鹅”事件,但中国金融监管不应忽视商业银行对利率的风险敞口。
传统银行理论认为,商业银行应该对冲利率风险,将自身利率风险敞口降为零,这是最优的利率风险管理策略。然而,Allen&Santomero(1997)[1]认为商业银行应该留有利率风险敞口,因为商业银行资本市场参与程度在提高,其风险管理策略也要更加主动。对商业银行利率风险敞口研究最早可以追溯到Flannery&James(1984)[2],他们使用回归分析估计商业银行股票收益率对利率水平的敏感性,并称之为利率beta,研究结果显示利率水平与股票收益率呈现出负相关的特征;之后,他们再使用截面回归分析研究利率beta和商业银行经营特征之间的关系,研究结果表明商业银行股票收益率对利率非常敏感,即商业银行存在利率风险敞口。在Flannery&James(1984)[2]之后,Saunders&Yourougou(1990)[3]和Kwan(1991)[4]也得出了类似的结论。之后,一些学者开始关注利率衍生工具对商业银行利率风险敞口的影响。代表性文献包括Choi&Elyasiani(1997)[5]&Hirtle(1997)[6]。Choi&Elyasiani(1997)[5]将汇率风险纳入分析框架,发现利率beta大小与利率衍生工具的使用具有正相关性。Hirtle(1997)[6]估计了商业银行年度利率beta,证明商业银行资产和负债结构影响利率风险敞口,且商业银行利率衍生工具使用越多,利率beta越大。
大多数学者的研究往往关注在利率风险的测度上,但没有将利率水平直接与商业银行违约概率相关联。近期与本文研究关联度较高的文献是I M F(2015)[7]。I M F(2015)[7]在使用K M V模型测度美国大型上市商业银行和保险公司违约概率后,研究测度的违约概率与美国货币政策和金融体系稳定的相关性。从国内来讲,将利率水平高低与银行业风险关联起来的研究相对较少,更多的国内学者的研究关注于商业银行利率风险管理层面(周颖和杨洁,2019[8];迟国泰和段翀,2017[9]),或者是关注货币政策对银行业风险的影响(柯孔林,2018[10];宋玉臣和乔木子,2016[11])。范晓云等(2018)[12]以利率为纽带,研究了人口结构与系统性风险之间的关系。刘志洋和李风鹏(2015)[13]研究利率水平与商业银行盈利水平的非线性关系。在大多数的研究中,学者往往针对利率的变化率来建模,然而利率水平的或高或低对商业银行的影响却并不相同。即使利率变化相同,但由于变化之前的基准不同,对商业银行的影响也不一致。在一个低利率的环境中,少量的利率上升或许对商业银行没有太大的影响;但如果利率水平本身就较高,则微小的利率上涨就会给银行体系稳定带来压力。本文在测算中国上市商业银行违约概率基础上,直接将利率水平与违约概率相关联,研究利率水平对商业银行违约概率的影响,为中国系统性风险管理提供政策建议。
二、商业银行违约概率估计方法
利率风险敞口的最终影响体现在银行经营风险上。由于中国尚未爆发大规模的银行业危机,因此如何测度商业银行经营风险是一个较大的挑战。以M erton期权定价理论为核心发展出来的或有权益分析(Contingent Claims Analysis,CCA)是金融危机之后测度金融系统性风险的主要方法之一。而KMV模型则是CCA方法的主要代表。
根据刘志洋(2017)[14]的观点,本文从微观的视角,使用KMV模型测算银行体系风险。KMV模型核心思想是将银行股票市值看作欧式看涨期权,当银行资产价值低于预期所需偿还债务的价值时,看涨期权作废,银行出现违约。虽然理论模型往往假设银行资产价格低于债务面值时银行倒闭,但银行倒闭也常常发生在资产价格较高的时期,此时银行往往因为流动性冲击而被迫抛售资产,因此本文针对KMV模型设定了违约触发值(用D B表示)。根据KMV模型的常规做法,本文对违约点的设定为:短期负债+0.5*长期负债。根据刘志洋(2017)[14],短期负债包括同业及其他金融机构存放款项、向中央银行借款、拆入资金、交易性金融负债、衍生金融负债、卖出回购资产款以及存款总量的20%;长期负债包括应交税费、应付利息、应付债券、递延所得税负债、预计负债、其他负债以及存款总量的80%。在风险中性测度下,银行股票价值为:
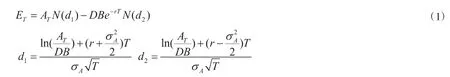
其中ET为银行股票市值,AT为银行资产市场价值,r为无风险利率,N()为标准正态分布累积函数,σA为资产市场价值标准差。假设银行资产市场价格服从对数正态分布,银行在T时间内唯一概率为:
由于DB不是日度数据,根据公开信息,频率最高的为季度频率,因此,本文DB的对应方式策略如下:每年1月、2月和3月的股票日度数据对应的是第一个季度的财报;4月、5月、6月的股票日度数据对应的是半年报;7月、8月、9月的股票日度数据对应的是第三个季度的财报;10月、11月、12月的股票日度数据对应的是银行年报。由于在使用KMV模型过程中需要商业银行股票日度波动率数据,因此本文使用Garc h(1,1)模型估计每家上市商业银行日度波动率。
三、商业银行违约概率估计结果
使用KMV模型需要股票收益率数据,因此本文的研究样本为中国上市商业银行,样本区间为2007年7月1日至2016年12月30日。虽然2016—2017年有江苏银行等9家城市商业银行上市,但考虑到样本量的问题,本文的研究样本仍选择在2016年之前上市的商业银行,具体包括中国工商银行、中国建设银行、中国银行、中国农业银行、交通银行、中信银行、光大银行、华夏银行、民生银行、兴业银行、浦发银行、平安银行、招商银行、北京银行、宁波银行和南京银行。
自从2005年中国政府进行银行业改革开始,中国商业银行经营市场化导向愈加明显。表1为各上市商业银行2007—2016年半年度KMV估计结果平均值。从表1可以看出,在特定时期,许多商业银行的违约概率都非常高。在2008年金融危机爆发之前至2008年下半年金融危机正式爆发,几乎所有上市商业银行的违约概率都在2008年下半年达到了最高值。华夏银行、平安银行、浦发银行和兴业银行甚至超过了10%,国有大型商业银行业超过了2%。危机爆发之后,中国政府采取积极措施稳定金融体系,中国上市商业银行的违约概率逐渐下降,到2016年下半年,下降至不到1%。可以说,中国上市商业银行违约风险整体较低。
自从2005年,有三个阶段商业银行利率风险较高:2008年6月至2009年6月;2012年12月至2013年12月;2015年下半年。在2008年6月至2009年6月,2008年金融危机爆发,金融市场流动性受到冲击,银行间市场融资成本上升,因此全世界银行业都受到负面影响,资本市场自然也会认为中国银行体系也受到了负面冲击。从2012年开始,中国人民银行逐渐放开存款利率和贷款利率,中国商业银行经营环境就此改变了,商业银行以往“躺着挣钱”的日子逐渐远去。在2013年5月,银行间市场同业拆解利率一直走高。在2013年6月20日,隔夜回购利率达到30%,银行体系风险达到高峰。在2015年10月24日,中国人民银行下调人民币贷款和存款基准利率,取消存款利率上限,完成了利率市场化最后一公里。从这些事件可以看出,中国商业银行违约概率上升与下降与中国利率市场化进程息息相关。在每一个利率市场化的关键阶段,商业银行违约概率都会上升,表明市场认为商业银行会面临更加严峻的挑战。因此了解利率对商业银行违约概率的影响对于监管当局至关重要。

续表1
四、贝叶斯向量自回归模型
向量自回归模型与传统计量经济学模型不同的地方在于其能够量化一个变量系统中,变量之间的相互影响。贝叶斯向量自回归模型进一步拓展了向量自回归模型,进一步提高了预测的精度,尤其在短期预测方面。传统向量自回归模型估计参数较多,为此常常需要假设许多参数为零。然而如此做法有时会得到与经济理论预测相反的结论。Litterman(1986)[15]首先提出了贝叶斯向量自回归模型,此模型使得参数逐渐收敛于零,而不是令其直接等于零。通过此方法,参数估计的准确度显著提高。在贝叶斯向量自回归模型中,所有参数被视为随机变量,在预测之前设定先验分布。本文分别设定四类先验分布进行实证分析。
首先,本文设定基准向量自回归模型:

其中yt包含M个时间序列变量,t=1,2,…..T,εt为相应的残差项,为α0为常数项,Aj为M*M系数矩阵。假设:

其中N表示正态分布。本文的四类先验分布设定如下:
第一,Jeffreys先验分布,如(4)式:

条件后验分布为(5)式:

其中,α为A的估计值,K等于M*P+1,为向量自回归模型待估系数总量,IW表示逆Wis h art分布。
第二,正态—Wis h art分布。正态—Wis h art分布是多元正态分布的共轭分布,均值和精度矩阵未知。假设

其中,N表示正态分布,均值为μ0,协方差矩阵为

W代表Wis h art分布。因此(μ,Λ)表示正态—Wis h art分布,见(6)式:

前两种分布假设需要输入参数较多。本文假设的第三种先验分布和第四种先验分布都来自SSVS(Stochastic Search Variable Selection)先验分布。SS V S先验分布只需要最少的参数输入,其基本思想是把先验分布分成一个等级,任何一个先验分布是两类分布的组合。假设αj为待估系数,则其先验分布可以写成(7)式

其中γj为等级变量。如果γj为1,说明αj主要来自第二个正态分布;如果γj为0,则αj主要来自第一个正态分布。K0j和K1j为先验方差,K0j往往取值较小,而K1j往往取值较大。因此SS V S先验分布对于所有估计参数α和Σ均设定了分布等级。如果只假设α是两个正态分布的组合,则称之为SSVS均值—Wishart先验分布(先验分布三)。如果同时假设α和Σ是两个分布的组合,则称之为SSVS均值—协方差先验分布(先验分布四)。
具体来讲,本文自回归模型设定见(8)式

其中,PDi,t表示商业银行i在t时刻的违约概率。IRj,t表示在时刻t的利率说。根据巴塞尔资本协议,商业银行利率风险指的是基准利率变化的风险,且由于在中国货币政策调控体系中,最长期限为5年,因此本文分别选择了1年期、2年期和5年期政府债券利率。PREt表示利率期限结构,为10年期国债收益率减1年期国债收益率。
在(8)式中,P为滞后阶数。本文的时间频率为日度数据,P选择为4。对于此类问题,大多数研究使用周度资本市场数据进行研究,而周度市场数据交易日为5天。然而本文使用的是日度数据来进行研究,进而增强提前预警能力,这意味着滞后阶数的选择必须小于5。然而,在一般的事件研究法中,事件窗口往往选择[-3,+3]或者[-2,+2],原因是给予市场参与者消化信息的时间。因此,本文假设市场参与者需要3天的时间来消化市场信息。最后,本文将滞后阶数定为4。
五、利率水平对商业银行违约概率影响实证分析
表2、表3和表4为模型的预测违约概率的结果。整体来讲,利率水平对各个上市商业银行违约概率的影响基本相同。根据表2、表3和表4,我们可以将违约概率分为低、中等和高三个类型。其中,低违约概率商业银行包括中国工商银行、招商银行、中国银行、建设银行和农业银行。高违约概率的银行为中信银行、华夏银行和南京银行。其余上市商业银行为中等违约概率。低违约概率的银行的违约概率基本集中在0.2%附近,且有四家为国有大型商业银行,这说明利率水平对国有大型商业银行的影响不是很大;而受利率水平影响较大的商业银行基本为股份制商业银行和城市商业银行。利率水平会影响商业银行的资产负债。随着中国利率市场化基本完成,股份制商业银行和城市商业银行由于网点分布的问题,在吸收存款方面会有挑战。在中国银行业,存款占据股份制和城市商业银行资金来源的70%以上,因此为了与国有大型商业银行竞争,股份制商业银行和城市商业银行存在提高存款利率的动机,进而增加了偿付能力风险。

表2 1年期利率对商业银行违约概率的预测
本文继续使用贝叶斯向量自回归研究每家上市商业银行违约概率对每一个期限利率的脉冲反应①由于版面原因,本文省略了脉冲反应图。。根据脉冲反应走向,本文将反应类型分为四种类型:①开始降低而后收敛至0(类型一);②开始上下波动而后收敛至0(类型二);③轻微上升(类型三);④显著上升(类型四)。表5、表6和表7为分类结果。总体来讲,利率水平上升对所有商业银行违约概率负面影响均较高,但处在类型四中的股份制商业银行和城市商业银行较多。
本文继续研究每家上市商业银行违约概率对利率期限溢价的脉冲反应②由于版面原因,脉冲反应图省略。。根据脉冲反应走势,本文将此脉冲反应归为五类:开始下降之后收敛至0(类型一);开始上下波动之后收敛至0(类型二);轻微上升或者没有明显反应(类型三);显著上升(类型四);轻微下降(类型五)。表8、表9和表10为分类结果。整体来讲,利率期限溢价对上市商业银行违约概率的负面影响不明显,但是南京银行、宁波银行、民生银行、浦发银行、兴业银行和光大银行受到负面冲击较为明显。在中国商业银行体系,有三分之一贷款为五年以上,因此当长期利率上涨高于短期利率时,商业银行盈利会增加,进而消除负面影响。

表3 2年期利率对商业银行违约概率的预测

表4 5年期利率对商业银行违约概率的预测

表5 上市商业银行违约概率对1年期利率脉冲反应归类

表6 上市商业银行违约概率对2年期利率脉冲反应归类
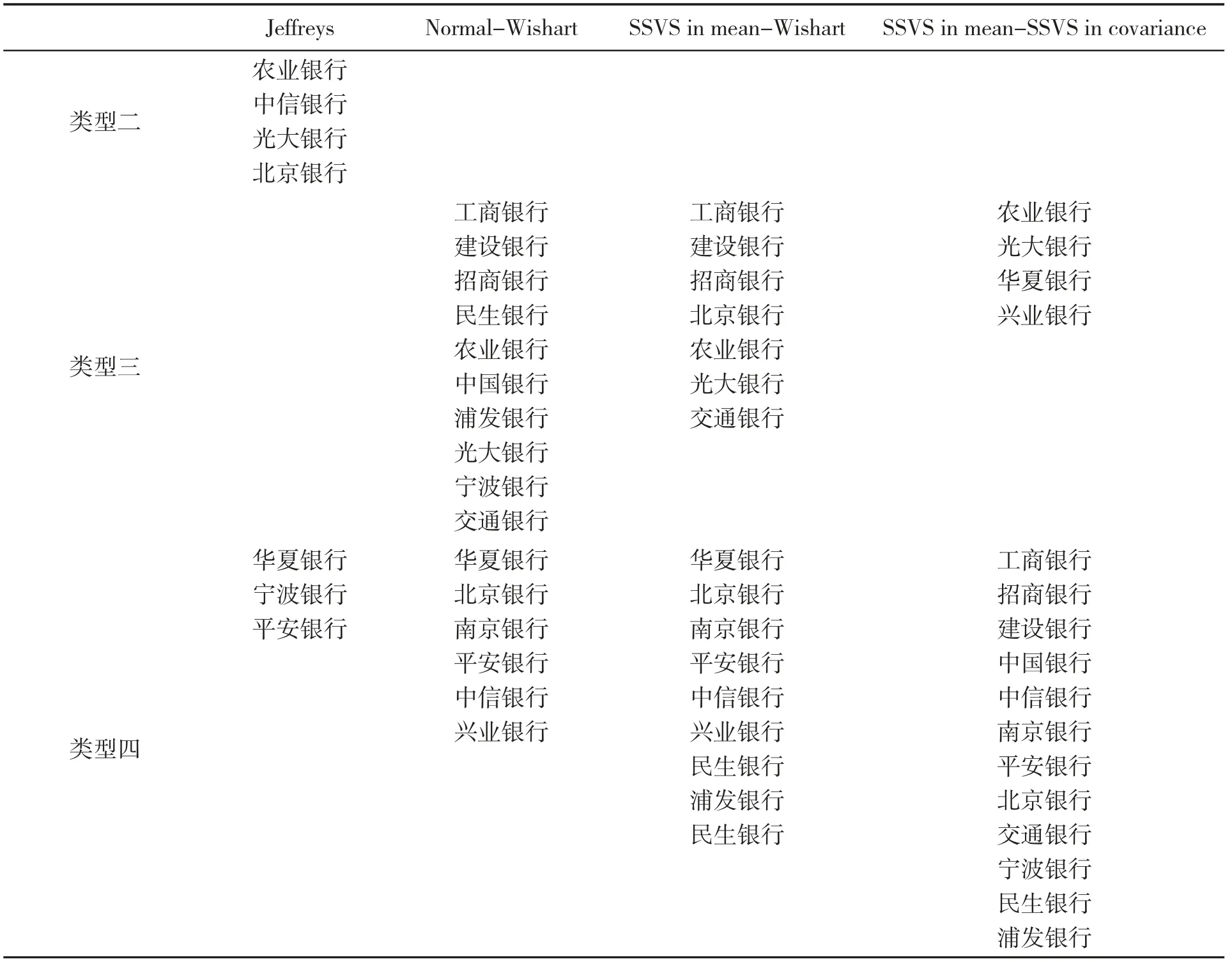
续表6
总体实证结果表明,国有大型商业银行受利率水平的影响程度小于股份制商业银行和城市商业银行。表11为2016年各个上市商业银行利率风险敞口报告。从第二列可以看出,国有大型商业银行1年至5年利率风险敞口与其对应期限资产比值是最低的,这与实证结论基本一致。从第三列可以看出,中国上市商业银行5年期以上利率风险敞口占比非常高,因此一旦长期利率上升,商业银行盈利能力必然显著上升,商业银行违约概率受利率期限溢价负面影响较小。从利息收入来看,当利率水平上升时,股份制商业银行和城市商业银行受到的负面影响较大。之所以股份制商业银行和城市商业银行受利率水平负面影响大,主要原因为:第一,国有大型行业银行占据银行体系的主导地位,政府声誉资本的注入无形间增加了商业银行资本水平,市场会认为国有大型商业银行是“大而不倒”的银行,因此利率水平如何变动,也很难改变市场的看法。第二,虽然当前中国互联网金融给银行体系带来冲击,但国有大型商业银行积极与主要互联网金融企业合作,比如,农业银行与百度、建设银行与阿里巴巴、工商银行与京东、中国银行与腾讯等。这些合作无疑会增加商业银行利率风险管理能力。从这方面来看,股份制商业银行和城市商业银行略微落后。

表7 上市商业银行违约概率对5年期利率脉冲反应归类

续表7
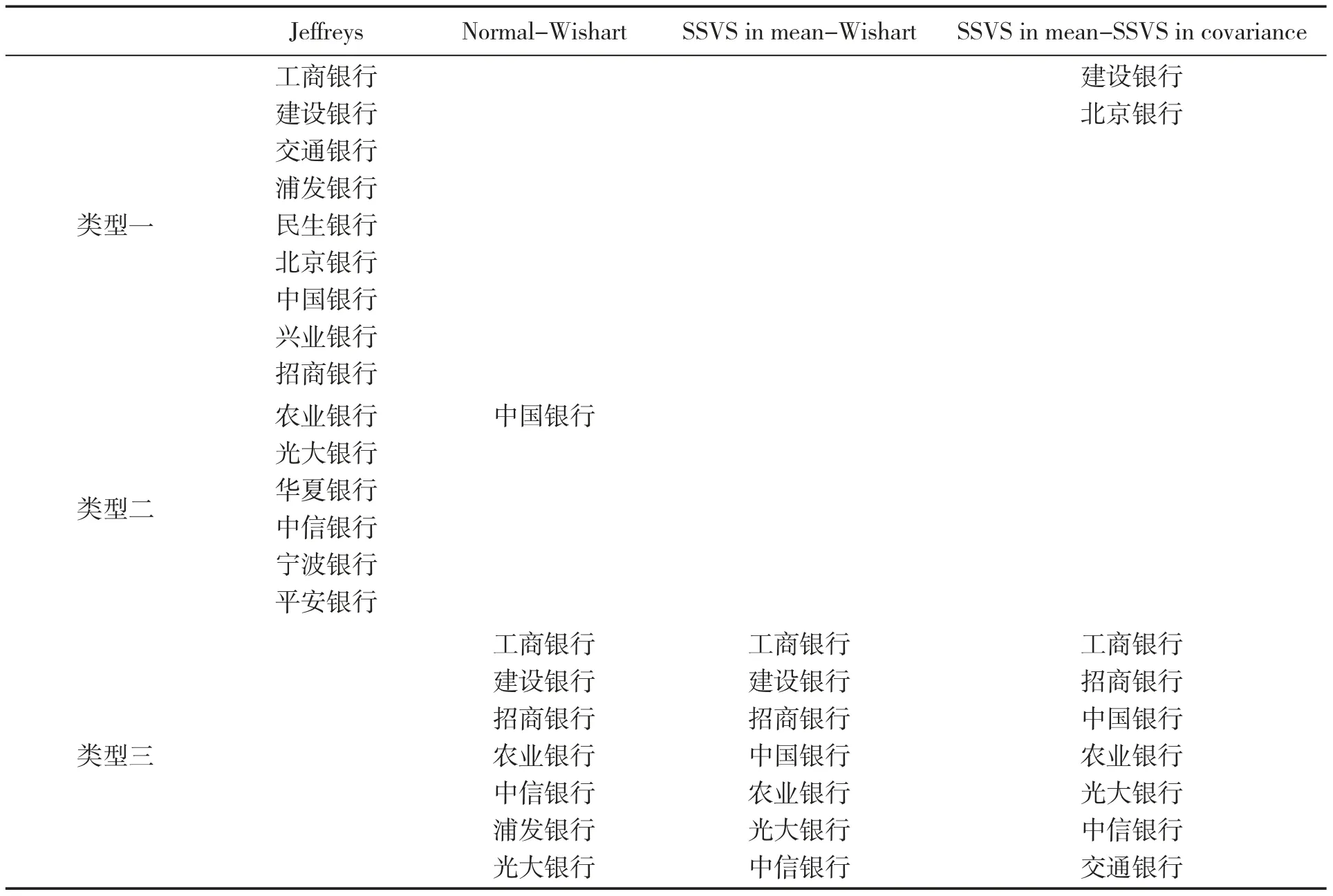
表8 商业银行违约概率对利率期限溢价的脉冲反应分类(1年期利率)

续表8

表9 商业银行违约概率对利率期限溢价的脉冲反应分类(2年期利率)

续表9

表10 商业银行违约概率对利率期限溢价的脉冲反应分类(5年期利率)

表11 2016年16家上市商业银行利率风险敞口与对应期限资产比值
六、结论
本文使用KMV模型计算了中国16家上市商业银行的违约概率,得到了时间序列数据,在此基础上,本文运用贝叶斯向量自回归模型研究1年期、2年期和5年期利率水平对商业银行违约概率的影响。整体结论表明,股份制商业银行和城市商业银行受利率水平负面影响较大,而期限溢价对商业银行违约概率负面影响较小。此结果对于中国银行业系统性风险管理具有参考价值。随着中国利率市场化基本完成,商业银行面临的利率风险会越来越高。对于这16家上市商业银行来讲,任何一家银行的倒闭都是系统性事件,因此中国金融监管当局不应仅仅根据规模来确定系统重要性银行,应该根据敞口规模来分析一家金融机构的系统性风险贡献度,进而防止系统性风险爆发。

