PM2.5对浙江、福建、江西房价的动态影响研究——基于函数型线性模型

周富杰， 叶景山， 黎哲镇， 温永仙

(福建农林大学 计算机与信息学院， 福州 350002)

通常情况下一个地区的房价主要受到5个方面的影响：①供求关系；②消费者个体因素；③住宅特征因素；④政府政策因素；⑤溢出效应[1]，其中住宅特征因素在以往的研究中主要集中在建筑特征因素[2]上。不过随着人们对生活品质、生活健康的要求越来越高，越来越多的人更加注重住宅特征因素中房屋周边的环境条件因素。PM2.5是衡量空气质量的一个重要指标。PM2.5对人类的健康有着重要的影响，因为PM2.5是指空气中极其细小的悬浮颗粒，这种细小的悬浮颗粒很容易通过呼吸进入人体的呼吸道甚至肺泡，不仅会对人体的呼吸系统直接带来极大的危害，而且还会诱发一些严重的慢性疾病。因此PM2.5已经成为影响房价的一个重要因素。

同时鉴于PM2.5数据的可获得性：自2015年的1月份起我国各个地级市每小时的PM2.5实时检测数据在互联网上发布，逐个小时逐个地市的PM2.5数据可以轻松的获得，数据在时间维度和空间纬度上都是极其详尽，而且该数据由政府相关部门整理发布真实可靠。国内已经陆续有学者在探讨、研究PM2.5与房价之间的关系：周梦天和王之[3]利用中国不同城市之间的PM2.5数据在时间和空间上的差异，经过一些列的稳健性检验，验证了PM2.5数据空气质量信息的公开对地区的房价存在长期稳定的影响；王亚冰[4]基于特征价格理论运用HEDONIC模型分析了北京PM2.5与房价之间的相互关系，最后也表明PM2.5虽然对北京的房价虽然影响较小，但是却显著存在。

虽然目前的研究已经表明了PM2.5对房价的影响较小却显著存在、长期稳定，但是既然PM2.5对于房价的影响是显著存在且长期稳定的，也就意味着PM2.5对房价的影响应当是在一段时间上持续稳定的影响。与此同时目前的研究还未对PM2.5与房价之间的关系进行动态上面的讨论，相较于之前基于整个时间段或者几个时段上讨论PM2.5与房价之间的关系，还可以更为详细的在每个时间点(每日)上讨论PM2.5与房价之间的动态关系。基于上述的原因，接下来将对PM2.5与房价之间的动态关系进行探讨和研究。

在对PM2.5与房价之间的动态关系进行探讨和研究中，我们采用了函数型线性模型，该模型的因变量为标量，自变量是由一组基函数线性组合而成的一个函数型数据变量。函数型数据不同于一般的时间序列，它可以通过一组基函数将离散时间点上的数据拟合为一条时间曲线，也正是如此函数型线性模型其实是对整条时间线的回归，因此可以通过这个特性考察自变量在一个时段上各个时间点对因变量的动态影响。

1 数据来源和数据特征

本论文通过自行编写的数据采集工具从互联网上收集了2018年浙江、福建、江西三个省份各个地市的12个月份每个月份的平均房价(单位：元/平方米)。不过由于江西省的鹰潭市和新余市，浙江省的丽水市，这些地市数据在收集过程出现数据缺失而且缺失的比较严重，因此没有包含在本次研究中。最终本次研究一共包含了三个省份29个地市。图1是这32个地市的房价曲线图，该图中的一条曲线就代表了一个地市月平均房价的变化趋势，曲线是使用函数型数据分析的方法[5]结合各地市每个月份上的月均房价拟合得到。通过观察图1可以发现2018年29个地市的房价都是相对比较稳定的，都是围绕着一个平均水平在一个比较小的范围内上下波动。

图1 29个地市月平均房价曲线图

对应的我们也收集了2018年浙江、福建、江西三个省份中29个地市全年PM2.5日值数据，数据来源于中国空气质量在线监测分析平台。图2是29个地市的PM2.5日值曲线图，该图中的一条曲线就代表了一个地市2018年的PM2.5的变化趋势，曲线是运用函数型数据分析的方法结合一年365天各地市的PM2.5日值数据拟合得到的。从图2可以看到PM2.5随着时间在不断升高和减小，形成一个个的波峰波谷，200天左右的PM2.5数值是最低的。出现这种情况的原因可能是：此时是6、7月份属于夏季，由于这些地区属于亚热带季风气候，在夏季会吹东南风，空气的流动性大因此空气中的PM2.5浓度会较低。

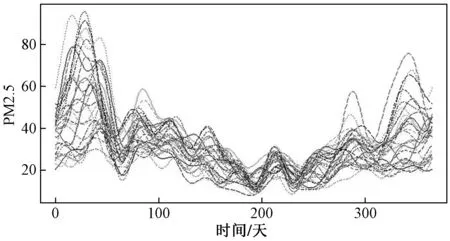
图2 29个地市PM2.5日值曲线图

2 函数型线性模型

本文所采用的函数型线性模型是因变量为标量，自变量为函数型数据的函数型线性模型，模型的具体形式如下：

(1)

ε表示随机误差，yi表示了第i个地市一年12个月的月均房价累计的以10为底的对数值。取对数是为了不改变数据变化趋势的同时又减小因为尺度大小不同而带来的差异；累加是为了将PM2.5对房价的影响效果聚集起来，如果PM2.5对房价存在显著影响累加后会更容易发现，同时因为PM2.5这种环境要素的效果必然存在一些滞后和持续的特性，直接考虑每日的PM2.5对全年的累积值既可以简化问题又不会丧失对这些因素的考虑。

β0代表截距项，xi(t)表示第i个地市的PM2.5在t∈[0,365]上的一个连续函数，当t=1,2,…，365时，就是对应的xi(t)在第1,2,…，365天上的PM2.5值，xi(t)本质上是通过一组基函将离散的日值PM2.5数据转化为光滑函数，设有一组基函数φk(t)，k=1,2,…，K，可以用这组基函数的线性组合的方式表示xi(t)：

(2)

基函数有多种选择方式，主要的选择方式有傅里叶基和B-样条基，本文选择傅里叶基。同样的β(t)，也是由一组基函数线性组合扩展开的：

(3)

3 PM2.5对房价的动态影响分析

3.1 动态增量分析

在进行模型分析之前先对2018年浙江、福建、江西三个省份中29个地市全年PM2.5的平均日值数据和12个月份每个月份的平均房价数据做出相位轨迹图。具体的做法是通过对转化成函数型数据的29个地市PM2.5的平均日值函数型数据和29个地市平均房价函数型数据求一次导数，直观上就是类似于求图1和图2中的均值曲线在各个点上的导数。29个地市PM2.5的平均日值数据的导数根据数学意义和目前的背景可以理解为：在极小一段时间内平均日值数据的增量，如果在某个时刻上导数是正的代表该时刻的PM2.5的平均日值是增加的；同理29个地市平均房价数据的数据也有类似的意义。这里将房价数据曲线上的12个月份的节点当作每个月份的最后一天，用原本的月份数据对日值数据进行粗略的估计以此得到PM2.5和房价对数值在相同时间上曲线的一阶导数值。通过这样的图形可以通过观察对应时间上数据点所落的象限知道两者的相互关系：如果数据点落在第一象限，PM2.5曲线导数大于零PM2.5上升，房价对数曲线导数大于零房价上升；如果数据点落在第二象限，PM2.5曲线导数小于零PM2.5下降，房价对数曲线导数大于零房价上升；如果数据点落在第三象限，PM2.5曲线导数小于零PM2.5下降，房价对数曲线导数小于零房价下降；如果数据点落在第四象限，PM2.5曲线导数大于零PM2.5上升，房价对数曲线导数小于零房价下降。下面给出全年的房价曲线一阶导数值对PM2.5曲线一阶导数值相位轨迹图，见图3。

图3 PM2.5对房价相位轨迹图

图3中的任意一个点就代表了一年365天中的某一天对应的房价曲线和PM2.5曲线导数值。从图中可以看出四个象限都有数据点分布，其中数据大部分集中在第二和第四象限：PM2.5曲线导数小于零PM2.5下降，房价对数曲线导数大于零房价上升；PM2.5曲线导数大于零PM2.5上升，房价对数曲线导数小于零房价下降。如果两者存在关联的关系那么就是，当PM2.5减少的时候，房价就会上升或者当PM2.5上升的时候房价就会下降。图形上如果标记每个数据点对应的时间标签能进一步研究趋势的时间分布和持续时长上的特点，但是数据点过于密集并不方便观察。因此我们将图像上的信息，统计为下表1的形式。

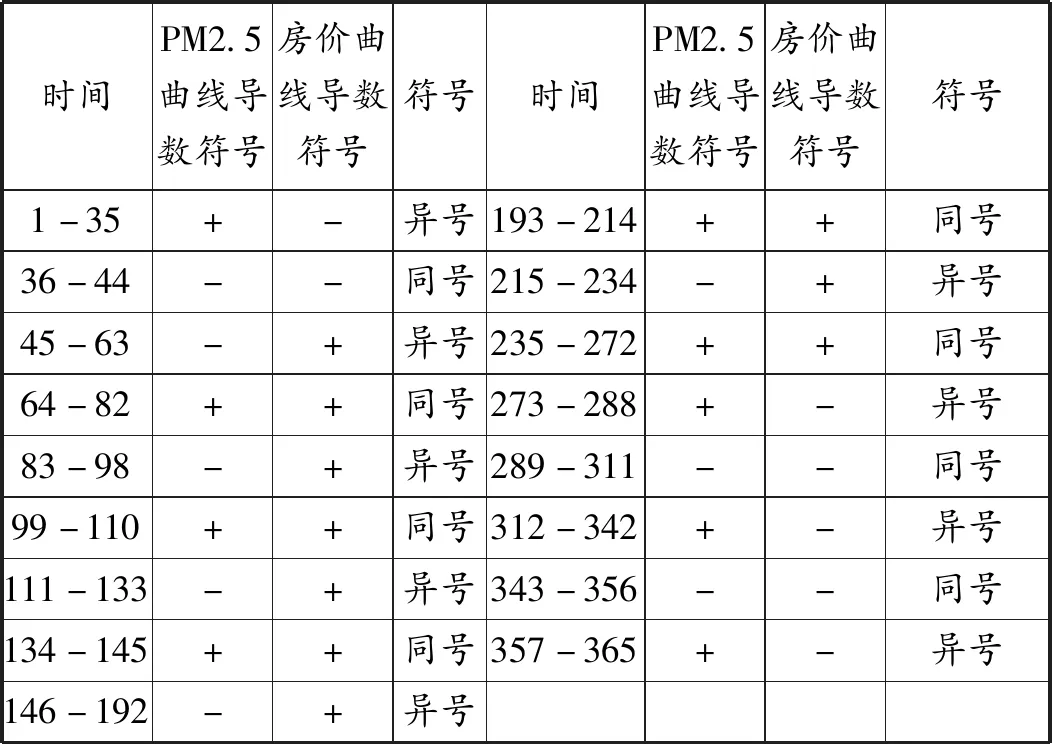
表1 导数符号与符号持续时长表

一共有216天的数据是异号的，也就是落在第二和第四象限，表明59%的数据存在一种类似负相关的关系；另外有149天落在第一和第三象限，存在一种类似正相关的关系，并且和负相关关系是交替出现的，这体现了一种交替的周期关系。从相位轨迹图我们得到了两者主要存在负相关关系的信息，以及在我们列出时段上两者各自的趋势，但是仍然无法下结论两者之间是否存在显著的相关关系，下面借由动态模型对此进行验证。

3.2 动态模型分析

表2 模型F检验表

F检验的P值为0.029<0.05，在0.05水平下是显著的说明两者是存在显著的相关关系或者说PM2.5日值数据可以作为预测平均房价累计对数值的变量，选取的模型是有意义的。同时也将模型的决定系数R2计算出来为0.709 4，意味着房价对数累计值70.94%的变异性是回归模型所引起的。

图4 PM2.5日值数据对房价累积值对数的效应值估计结果

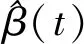
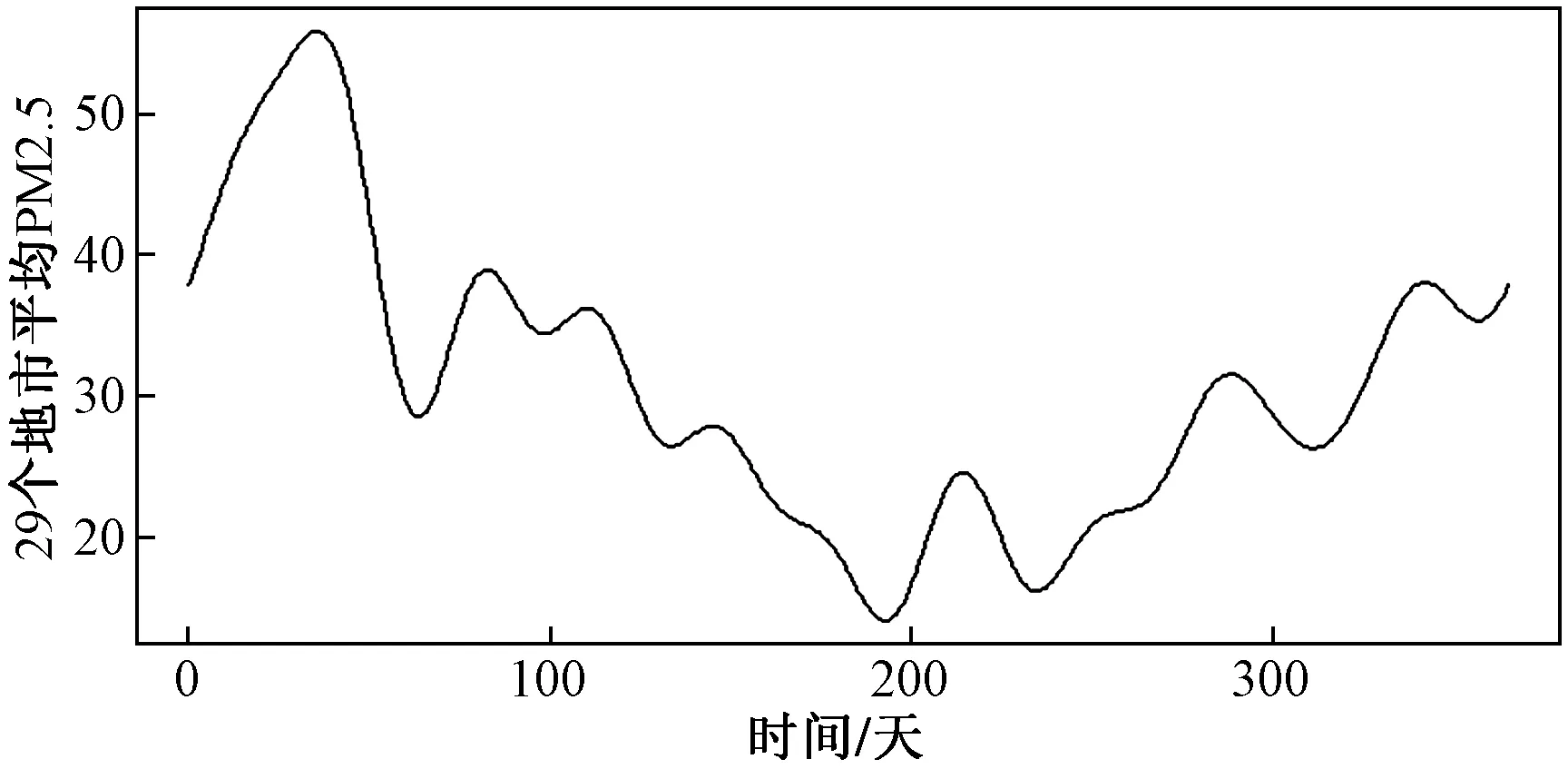
图5 29个地市平均PM2.5日值数据曲线

最后为了便于观察实际的情况，我们将图4和图5的曲线X轴的位置严格对应，但是Y轴的值仅保留它们的变化趋势，通过合理的上下平移和缩小图5中Y轴上的值将两张图放在一起，合并为图6。从图6中可以很明显的看到在第1到54天、第95天到151天，第212天到267天，第297天到365天这个4个区间上当一条曲线上升另一个曲线就下降，表现在PM2.5和效应值上就是当PM2.5上升的时候效应值就往负的方向增长，当PM2.5下降的时候效应值就往正的方向增长，也就是PM2.5的上升最终会引起房价下降，PM2.5的下降最终会让房价逐渐回升；另外在第54天到第95天，第151天到212天，第267天到297天这三个时间段内，效应值的变化趋势和PM2.5的变化趋势一同上升或者一同下降，也就是表现为PM2.5上升最终会带动房价上升，PM2.5下降最终会带动房价下降。

图6 图4和图5趋势融合图

3.3 正相关趋势探讨

在3.2和3.1中都出现了一种有违认知常理的趋势，就是PM2.5的升高最终会带动房价的升高。按照正常的思维PM2.5越高周边的居住环境越差，然后导致购房人的购买欲望下降，房价最终是要下降。所以如果该趋势是客观存在的应当是与PM2.5相关的一些因素所引起的，然后表现为PM2.5上升房价也跟着上升。会导致PM2.5上升同时又有利于房价上涨的因素有：①交通因素。各类交通工具在使用的过程中，燃烧燃料排放的尾气会导致PM2.5上升。如果房屋周边的交通发达、车流量大，会因为交通的便利性使得房价上升。②餐饮因素。餐饮业烹调过程中天然气、煤的燃烧以及烹调过程中产生的油烟也会产生PM2.5，餐饮业的发达说明当地的人流量大、人员密集，这也会导致房价上涨。③其他因素。一些与PM2.5的趋势重叠但是与PM2.5并不相关的其他因素，比如人们的交易偏好在那些时间段里面的交易量持续上涨导致房价的上升或者正如Burnside, Eichenbaum和Rebelo研究所表明的房价的暴涨与投资者过度乐观的情绪相关[6]的情形类似——这是一种心理因素的作用，PM2.5值很小导致房价上涨到一定程度即使消费者再喜欢这边的环境也不打算购买因为已经超出他们的心理预期，交易量减少又导致房价下降，所以PM2.5值的下降反而导致房价下降； PM2.5值超过了一定标准让房价持续下跌，当房价跌到一定程度的时候消费者觉得有利可图反而大力购进导致成交量上涨，又反过来提升了房价。上述提到的3种因素都是导致这种负相关趋势出现的可能原因，但是鉴于正相关关系往往是和负相关关系交替出现，而且心理因素正好也有这种围绕着价格周而复始变化的特点，因此在上述提到的因素中最有可能的应当是心理因素。

4 结论与讨论

经过本文的研究，总的来说PM2.5对浙江、福建、江西房价的动态影响存在两种不同的影响模式：一种是PM2.5的上升最终会导致房价的下降，PM2.5下降最终会导致房价上升，这个符合客观规律也就是PM2.5越小就代表房屋周围的空气质量越好，消费者自然更愿意购买以及愿意出更高的价格；另一种是PM2.5的上升最终会带动房价的上升，PM2.5的下降会最终导致房价下降，这是有违常识的，应当是其他因素导致了这些时间段上房价的变化趋势而刚好与PM2.5的变化趋势重合。出现这种趋势的时间段是第54天到第95天，第125天到212天，第267天到297天，时间跨度大又是间隔出现应当不是自然要素起作用，比较可能是人为因素导致。在通过对多个会导致PM2.5上升同时又有利于房价上涨的因素进行比较后发现由房屋价格变动导致的心理因素最有可能是该种趋势的成因。