我国上市商业银行全要素生产率的测算与分析

邱 鹏

(中国社会科学院 研究生院， 北京100033)

1 文献综述

全要素生产率(Total Factor Productivity，简称TFP)主要测算将投入转化为产出的厂商绩效，是指要素投入不能解释的部分，代表了一个企业的综合效率水平和生产力水平。计算全要素生产率的方法有参数方法、半参数方法和非参数方法。鲁晓东采用GMM参数方法估计了我国经济的全要素生产率[1]。鲁晓东，连玉君在微观企业层面，采用最小二乘法和固定效应参数方法，以及OP和LP半参数方法计算了工业企业的全要素生产率[2]。杨汝岱采用OP和LP半参数方法计算了工业企业层面的全要素生产率[3]。蔡月洲、郭梅军采用DEA非参数方法对上市商业银行的全要素生产率进行了测算及分解[4]。沈悦、郭品采用DEA非参数方法计算了商业银行全要素生产率[5]。综合上述方法，半参数方法解决了参数方法中模型的内生性问题，而非参数方法的优点是不需要知道生产函数具体形式，但无法测度某一因素对效率测度值的影响。

对全要素生产率进行测算，第一步先要选取投入产出指标，由于商业银行的生产经营不同于工业企业，如何选取投入产出指标，学术界分歧比较大，目前主要有生产法、收支法和中介法。生产法从银行的各类商业活动和为客户提供服务的角度，选取贷款数量、交易活动等变量为产出指标，选取实物性的投入，如资本、劳动为投入指标。收支法从银行的盈利能力以及与之相关的各类支出角度，选取利息收入和非利息收入等变量为产出指标，选取利息支出为投入指标。中介法从商业银行在储户和贷款人之间起到融通资金的中介作用的角度，选取利息非利息收入、贷款数量为产出指标，选取利息及非利息成本为投入指标。蔡月洲、郭梅军采用中介法，产出变量选择：利息收入、非利息收入、贷款总额。投入变量选择：利息支出、营业支出、存款总额[4]。沈悦、郭品投入变量选择：资产总额、营业费用[5]。产出变量选择：税前利润、贷款总额。中间变量选择：存款总额。本文认为产出变量选择“税前利润”和投入变量选择“在职人数”是不合适的，从实践中来看，由于劳动法对于劳动者的保护，银行不能随便的解雇员工，当银行利润减少的时候，不能通过解雇员工，尤其对于国有银行，而且银行业不是劳动密集型行业，单纯的靠增加劳动力是不能够增加利润的，劳动力人数已经不再是产出的影响因素。税前利润是通过对期间经营数据的计算才能得到，尹恒、柳荻、李世刚认为要使增加值成为有效的分析工具，需要满足5个不近现实的假设，用增加值估计企业全要素生产率是不合适的[6]。因此，产出变量应采用能直接获得的数据，例如总产值或销售收入。

本文将基于柯布道格拉斯生产函数，比较采用Olley-Pakes半参数估计方法和Levinsohn-Petrin半参数估计方法。对目前已经上市的32家商业银行(包括国有大型商业银行、全国股份制商业银行、城市商业银行和农村商业银行)在2009-2018年间全要素生产率进行测算，对全要素生产率的变动情况进行实证分析，并对实证结果做进一步的解释。

2 全要素生产率的估计原理

2.1 柯布道格拉斯生产函数

为了研究上市商业银行的全要素生产率，本文采用1928年美国数学家柯布和经济学家道格拉斯提出的生产函数，假设商业银行业符合函数中的科技进步、劳动和资本之间的关系。该生产函数的数学形式如下，其中Y为产出，L为劳动投入，K为资本投入，A为全要素生产率：

(1)

两边取对数，其中μit为随机误差项：lnYit=lnAit+αlnLit+βlnKit+μit

(2)

(3)

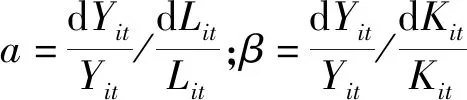
(4)

α为Y对于L的弹性，即L变化1%，影响Y变化百分率；而β为Y对于K的弹性，即K变化1%，影响Y变化百分率。

令lnAit=ωit，lnYit=yit，lnLit=lit，lnKit=kit得到如下方程，其中ωit为企业可以观测到的全要素生产率，代表企业的管理水平、技术等因素：

yit=αlit+βkit+ωit+μit

(5)

如果采用经典最小二乘法对方程(5)进行估计，就会存在内生性的问题和选择性偏差。内生性问题是由于企业会根据生产率的信息来决定投资，而投资会形成资本，导致ωit与kit相关。选择性偏差是指由于企业进入和退出市场，而且企业资本同企业退出市场可能性之间的负相关关系，使传统的回归方法低估资本的系数而高估了劳动投入的系数。为了解决这两个问题，拟采用如下两种半参数估计方法。

2.2 Olley-Pakes半参数估计方法

该方法由Olley和Pakes在1996年的一篇研究美国电讯设备行业的全要素生产率的论文中提出[7]。该方法的第一个核心假设是：在资本存量一定的条件下，且企业每年的投资值大于0，投资是关于生产率的严格单调增函数，投资量的大小反映了企业全要素生产率的高低，即：

iit=itt(kit,ωit)

(6)

为解决模型估计中的内生性问题，将(6)中的生产率求解出来，将ωit表示为iit和kit的函数，即用(6)式的反函数将ωit显性地表示出来。

(7)

Olley-Pakes的第二个核心假设是企业生产率的变化服从外生的一阶马尔科夫过程，即企业对下一期的生产率的预测只与当期的生产率有关，即E[ωi t+1|ωit]，因此可以将当期生产率写成上期生产率的条件期望与误差项的和，其中g(ωi t-1)表示关于ωi t-1的函数，ξit表示t-1期与t期之间的误差项：

ωit=E[ωi t|ωit-1]+ξit=g(ωi t-1) +ξit

(8)

Olley-Pakes认为劳动力为自由变量，只影响当期的产出，不会影响下期的产出，资本是一种累积存量要素，当期的投资下一期才会形成资本，即：

kt=(1-δ)kt-1+it-1

(9)

Olley和Pakes估计的第一阶段将(7)带入到(5)中得：

yit=αlit+βkit+ht(kit,iit)+μit

(10)

由于ht的表达式中包含资本要素kit，所以无法在(9)中识别出β。令：

φt=βkit+ht(kit,iit)

(11)

将(11)带入(10)中得到:

yit=αlit+φt(kit,iit)+μit

(12)

由于用关于资本和投资的函数φt将生产率显性地表示出来，所以式(12)中不存在任何内生性问题。虽然φt的具体形式未知，但通过非参计量中用i和k的二阶多项式来近似，得到劳动力的系数估计值和φt的估计值

Olley-Pakes估计的第二阶段，由(7)和(11)得：

ωit=ht(kit,iit) =φt-βkit

(13)

(14)

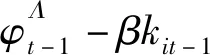
Olley-Pakes的方法中假设投资是关于生产率的严格单调增函数，而实际生产中企业资产达到一定规模后就暂缓投资了，一段时间内投资为0，因此该假设在实际生产中并不成立，而且该方法必须要有企业进入和退出，而我国上市的商业银行还没有摘牌退市的情况发生，因此无法直接应用Olley-Pakes的全要素生产率的估计方法，下面介绍的Levinsohn-Petrin半参数估计方法对上述不足进行了改进，因此应用更加广泛。

2.3 Levinsohn-Petrin半参数估计方法

(15)

Stata中，产出的增加值或者总收入设置为被解释变量；资本存量设置为capital变量；中间投入设置为代理变量；劳动和企业规模、时间、行业等虚拟变量设置为自由变量。

3 数据和变量说明

3.1 数据来源

本文以我国上市商业银行为研究对象，选取了6家国有大型商业银行、9家全国股份制商业银行、11家城市商业银行和6家农村商业银行，共32家已经在境内公开上市的商业银行，数据来源wind数据库，数据期间为2009-2018这10年，对样本进行了筛选，去除了某年数据缺失的样本，因此为非平衡面板。数据选择的优势：①所选银行类型覆盖面全，能够代表我国银行业最先进的生产率水平。②数据期间覆盖国有商业股份制改造启动后的区间，包括了商业银行飞速发展期，经济发展进入新常态时期和供给侧结构性改革实施后的时期，有利于考察各个时期的政策对商业银行全要素生产率的影响。③所有数据都是wind从各个银行公开发布的年报中收集，数据的可信性和可比性较高。④采用面板数据，在不同时间上选择不同规模的银行数据作为样本观测值，可以分析全要素生产率与企业规模的关系。

3.2 入产出指标选取

在目前存贷利息差仍是商业银行主要盈利来源的情况下，商业银行生产经营分为资产业务和负债业务，作为金融中介，商业银行的效率主要体现在成本收入比。本文主要借鉴中介法、生产法和收支法的变量，拟选取投入和产出变量如下：

1)产出变量R：营业收入，该指标为总产值或者总收入。

2)投入变量E：营业支出。

3)投入变量K：银行年末总资产。

4)中间投入变量D：由于Olley-Pakes方法和Levinsohn-Petrin方法中，都要求中间投入变量是生产率和投入变量K的严格单调函数，因此本文采用计息负债。我国商业银行主要靠吸收存款，发放贷款，依靠存贷差来获取收益。一个银行总资产越大，人们越觉得安全，因此更愿意将钱存到大银行，大银行更容易吸收到存款，因此负债D与总资产K相关。同时由于银行吸收存款也是有成本的，只有生产率高、盈利能力强的银行才有动力去吸收更多的存款。因此负债D与生产率ω相关。D是K与ω的函数，且是ω的单调递增函数。负债与产出相关性不高，因为负债多，成本也高，有可能使产出变小，也有可能通过贷款，使产出变大。

5)虚拟变量：Timedum3来区分供给侧结构性改革前后，银行全要素生产率的变化情况，供给侧结构性改革2015年11月10日中央经济工作会议提出，2016全面实施，因此，2015年及其以前设置为0，2016年及以后设置为1。

以上统计数据为当年价格的名义值，本文利用GDP平减指数进行调整，以2009年的GDP价格指数为基期，将名义值进行不变价格调整。

4 上市商业银行全要素生产率实证结果及分析

4.1 总资产K和营业支出E对营业收入R的回归分析

实证模型设定如下：

lnRit=αlnEit+βlnKit+ωit+timedum3+μit

(17)

采用LP半参数方法得到表1所示的回归结果：

1)lnE的结果分析：拒绝概率P小于0.01，lnE的系数显著，拒绝α=0的假设，接受=0.42，即营业支出每增加1%，营业收入增加0.42%。从实践中来看，营业支出中占比最大的是管理费用，而银行业员工的工资薪酬福利都计入管理费，以工商银行2016年年报数据为例，管理费用占营业支出的比重达55.5%，因此，增加员工工资和福利待遇，有利于激发员工的工作积极性，能够增加营业收入。

4)timedum3的结果分析：拒绝概率P小于0.01，timedum3的系数显著，因此在供给侧结构性改革实施前后，我国商业银行的产出有显著的变化。

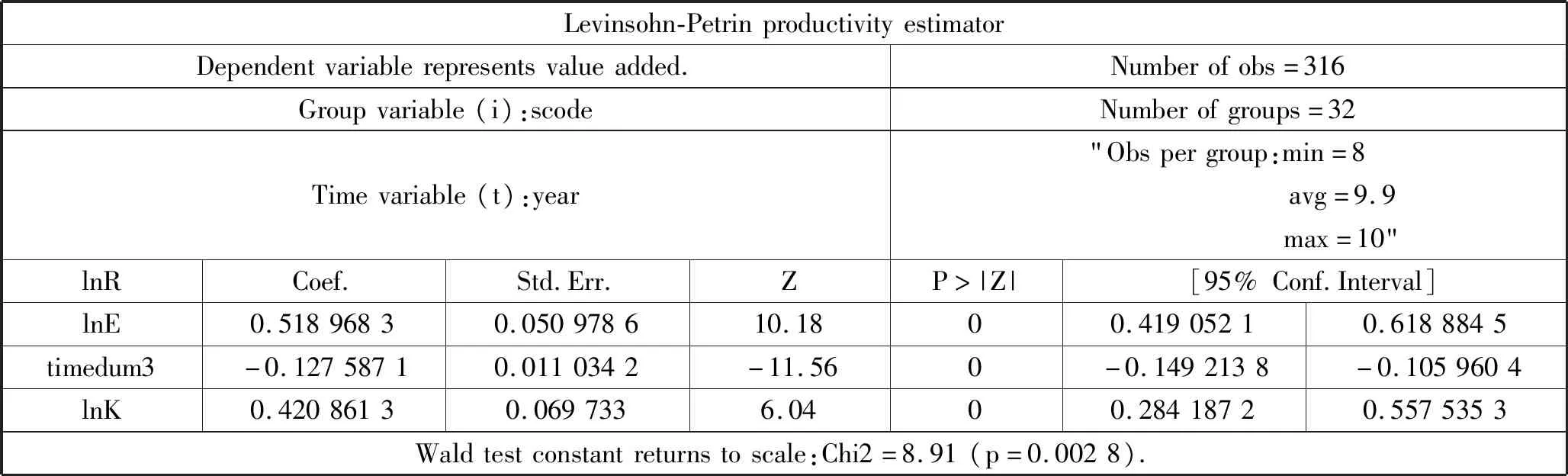
表1 LP半参数方法回归结果

4.2 上市商业银行全要素生产率变化分析

4.2.1 上市商业银行全要素生产率的变化趋势分析

通过公式(15)计算我国上市商业银行全要素生产率，如表2，十年来各家商业银行的全要素生产率平均值为0.57，最小值为0.38，最大值为0.83。通过计算各年度的商业银行全要素生产率的几何平均值，如图1，我国上市商业银行的全要素生产率从2009年到2013年都在逐步提高，随着我国经济发展进入新常态，从2014年开始下降，在2016年开始实施供给侧结构性改革后，我国上市商业银行的全要素生产率开始稳步提高，由此可见，商业银行的经营效率与我国经济发展紧密相关。

表2 我国上市商业银行全要素生产率的统计特征

图1 我国上市商业银行全要素生产率的变化

4.2.2 根据商业银行的分类比较分析全要素生产率

如图2所示，国有大型商业银行的全要素生产率最高，股份制商业银行次之，城市商业银行第三，农村商业银行最低。国有大型商业银行是我国金融业的中流砥柱，成立时间长，资产规模大，科技处于行业领先，公司治理完善，制度健全，因此国有大型商业银行的全要素生产率最高。股份制商业银行依靠其灵活的体制机制，以业绩为导向，充分发挥员工的积极性，因此其全要素生产率也是较高的。城市商业银行和农村商业银行由于业务仅仅局限某一区域范围，资产规模小，其前身分别由城市信用社和农村合作银行改制而来，因此全要素生产率较低。

图2 我国上市商业银行全要素生产率的变化

5 结论与建议

根据前面第四部分的实证分析，可以得出以下结论和建议。

一是，我国商业银行的产出指标——营业收入与总资产和营业支出正相关，而营业支出中员工薪酬能够占到三分之二，商业银行生产率与员工的生产率密切相关，通过提高员工待遇，激发员工工作积极性，高薪吸引人才，必将提高商业银行的全要素生产力。

二是，近十年商业银行全要素生产率有升有降，前期商业银行的全要素生产率随着我国经济的高速发展而逐步提高。但由于我国经济发展进入新常态等各种内外部环境的影响，我国经济增速的放缓使商业银行全要素生产率也随之下降，而经过供给侧结构性改革后，我国商业银行的风险得到化解，能够更好地服务于实体经济，商业银行的全要素生产率逐步提高，使得商业银行服务实体经济效率水平得到提升。

三是，商业银行的全要素生产率与银行的规模有明显的相关性，六大国有商业银行的全要素生产率最高，代表了我国商业银行最先进的生产力水平，其他商业银行应努力向国有商业银行学习。