两类2-Toeplitz 型矩阵的奇异值

过美林， 钟金

（江西理工大学理学院，江西 赣州341000）

0 引 言

奇异值分解是一种重要的矩阵分解法，在矩阵分析、数值代数、扰动理论、最小二乘问题等数学分支中有重要的理论意义[1-2]，同时在许多应用领域，如人脸识别方法、信号处理、图像处理、声源识别、降噪方法等领域有重要应用[3-9]。由于奇异值及奇异值分解重要的理论意义和应用价值，如何确定矩阵的奇异值及其分解显得非常重要。 近年来，一些具有特殊结构矩阵的特征值分解和奇异值分解得到广泛关注和研究，特别是利用矩阵的特征值分解给出了这些特殊结构矩阵的幂，如文献[10]和[11]分别计算了一类偶数阶和奇数阶对称三对角矩阵的正整数次幂；文献[12]计算了三对角2-Toeplitz 矩阵的幂；文献[13]计算了复五对角2-Toeplitz 矩阵的整数次幂；文献[14]从三次循环多项式序列的特征关系出发研究了偶数阶五对角2-Toeplitz 矩阵的特征值及特征向量， 进而得到了其整数次幂；文献[15]计算了一般三对角矩阵的幂；文献[16]计算了r-周期三对角矩阵的特征值。此外,文献[17]和文献[18]分别计算了双对角过滤矩阵和梳子过滤矩阵的奇异值分解。

目前关于特殊结构矩阵的研究主要集中于求特征值及特征值分解， 对奇异值及其分解研究较少。文章将通过几类具有特殊结构矩阵的特征值分解给出两类2-Toeplitz 型矩阵的奇异值。

1 奇异值及奇异值分解的定义

用Mm，n表示m×n 复矩阵的集合，若m=n，则记为Mn，A*表示A 的共轭转置， 若矩阵A∈Mn满足AA*=A*A=I，则称A 为酉矩阵，其中I 是单位矩阵。设A∈Mm，n，若m≥n，则半正定矩阵A*A 的特征值的非负平方根称为A 的奇异值；若m＜n，则半正定矩阵AA*的特征值的非负平方根称为A 的奇异值。用s1（A）≥s2（A）≥…≥sp（A）表示A∈Mm，n的奇异值，并记s（A）=（s1（A），…，sp（A）），对角矩阵的记号为diag{s1，s2，…，sp}，注意该符号也可以表示长方阵。 显然奇异值是酉不变的， 即对于任意A∈Mm，n及任意酉矩阵U，V∈Mn，s（UAV）=s（A）。 因此，正规矩阵的奇异值就是它的特征值的模。 特别的，对于半正定矩阵，奇异值和特征值是一样的。

定义1[2]（奇异值分解）设A∈Mm，n，则存在酉矩阵U∈Mm和酉矩阵V∈Mn使得：

UAV=diag{s1，s2，…，sp}，

其中，s1≥s2≥…≥sp≥0，p=min{m，n}。

2 两类2-Toeplitz 型矩阵的奇异值

本节给出两类2-Toeplitz 型矩阵的奇异值，首先给出下面引理。

引理1[11]奇数阶三对角2-Toeplitz 矩阵

的特征值为：

由此可知，Bn的特征值全为实数，且重数为1。

定理1设n 为整数，t0，t1，l0，l1为非零复数，Tn，n+1是n×（n+1）（n=2m+1，m∈N）的2-Toeplitz型矩阵

则它的奇异值为：

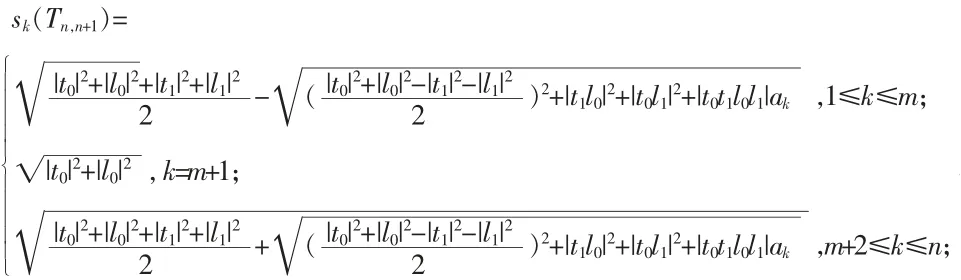
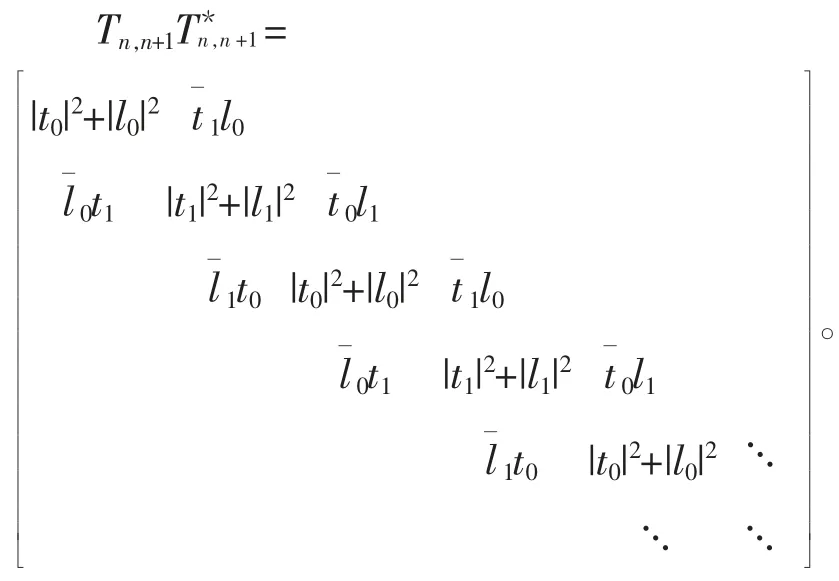
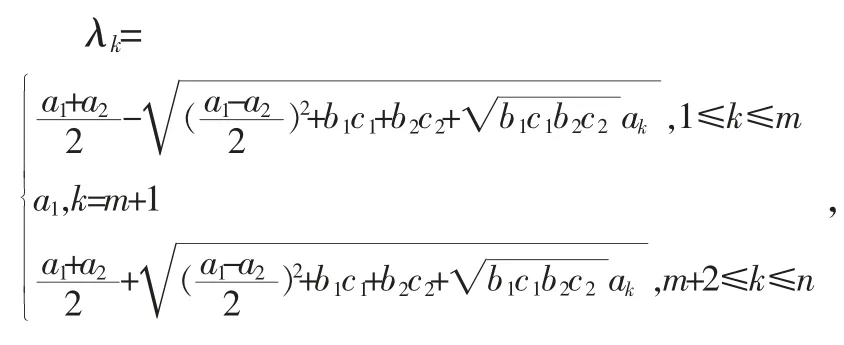
于是，

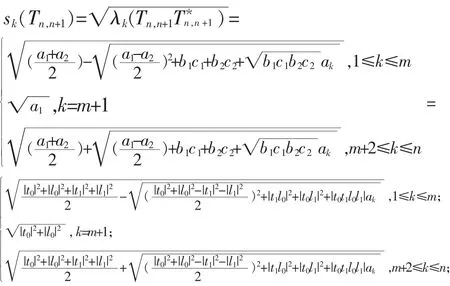
下面给出另一种2-Toeplitz 型矩阵的奇异值，这类矩阵与前一类矩阵相比，非对角线元素整体向右上方平移了一条线。

定理2设n 为整数，p0，p1，l0，l1为非零复数，Pn，n+2是n×（n+2）（n=2t，t∈N）矩阵

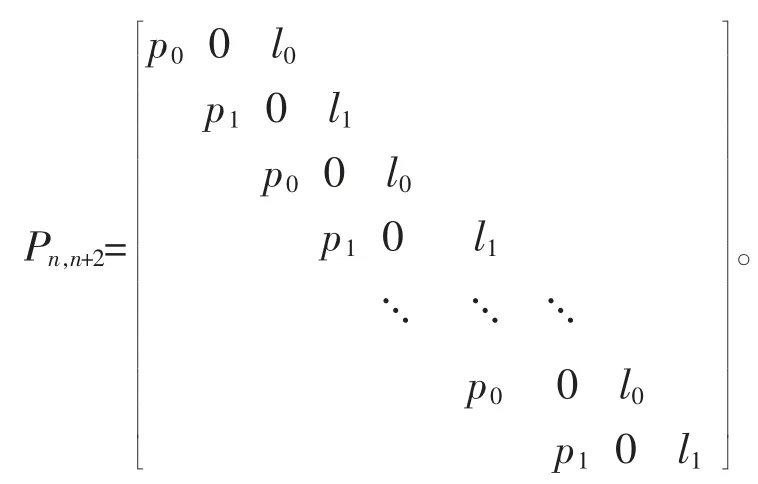
则它的奇异值为：

证 明：由文献[13]知，对于偶数阶五对角2-Toeplitz 矩阵

n=2t，（n∈N）。

考虑多项式序列{Ai}i≥0，{Bi}i≥0，它们具有三阶循环的特征关系：

其中，初始条件为A0（x）=0，A1（x）=1，以及

由式（1）,式（2）两式的关系式可得：

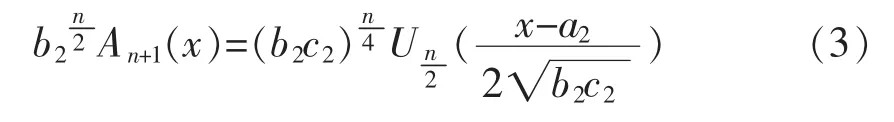
和

其中，n=2t（t∈N），Un（·）是n 次第二类切比雪夫多项式

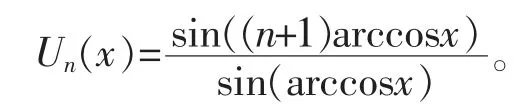
Un（x）的所有根都包含在区间[-1，1]内。

由式（1）,式（2）两式的关系式可得：

其中，Pn-1（x）=[P0（x），P1（x），P2（x），…，Pn-1（x）]T，且

由于Pn是n 阶五对角2-Toeplitz 矩阵，对应于式（5）中等式的多项式Pn+1，假设Pn+1具有简单的零解，则Pn的特征多项式为：

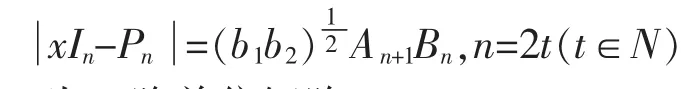
其中，In为n 阶单位矩阵。

由式（3）、式（4）及上式可得：

所以矩阵Pn的特征值为：

由于

所以，

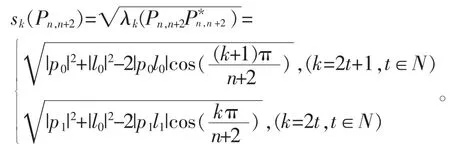
3 结 论

矩阵的奇异值及奇异值分解不仅是矩阵理论中的重要内容， 同时在许多应用领域有重要应用，然而， 矩阵的奇异值及奇异值分解并不容易求得。文章的研究表明某些特殊结构矩阵的奇异值可通过某些特殊结构矩阵的特征值分解求得，如利用三对角和五对角2-Toeplitz 矩阵的特征值可得到两类2-Toeplitz 型长方矩阵的奇异值，这种方法对于求解其他特殊结构矩阵的奇异值有很好的参考价值。然而该方法并不能求出这两类矩阵的奇异值分解，即求出相应的左右酉矩阵，这将是下一步的研究工作。