一类自由振动方程的定解问题

许佰雁

（长春光华学院基础部，吉林长春130033）

积分变换法广泛应用于求解无界区域或半无界区域的定解问题，如波动方程、热传导方程、泊松方程等[1-4]。将利用傅里叶变换法，证明一类自由振动方程的定解问题。

定义1若f(x)在(-∞,+∞)上有定义，在任一有限区间上满足狄利克莱条件，且绝对可积，则称

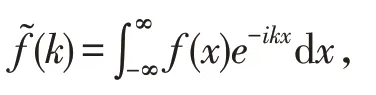
为f(x)的傅里叶变换，记为

定义2称

为f(x)的傅里叶逆变换。

引理1若a1,a2为任意常数，则对任意函数f1(x),f2(x)，有

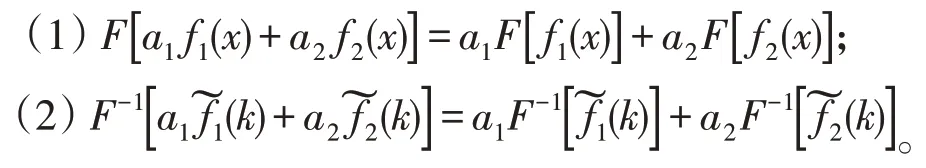
证明（1）由定义1知：

（2）同理可证。

定义3称

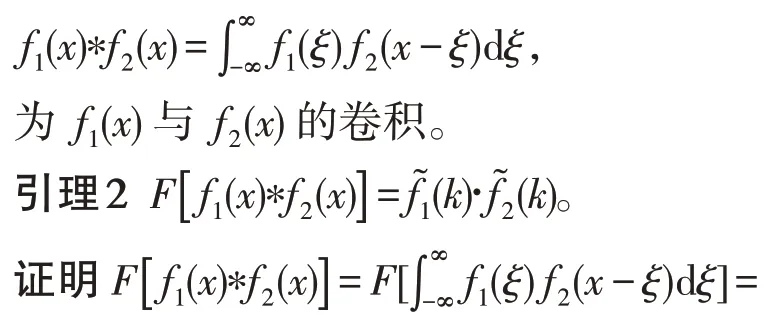
引理3（菲涅尔积分）

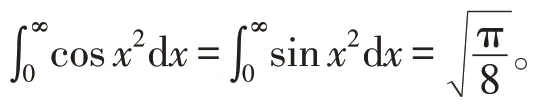
证明见文献[2]

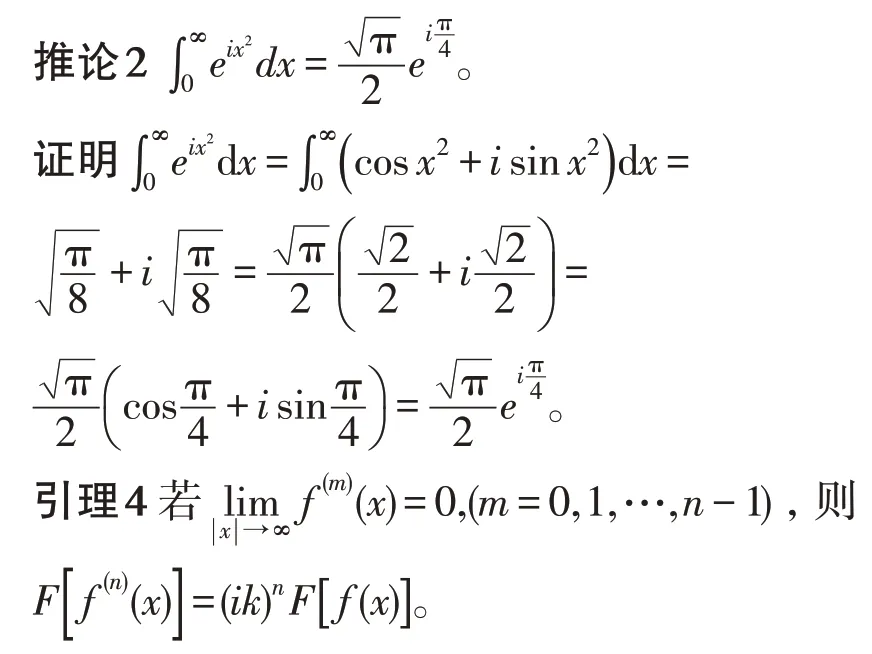
对于无限长梁在初位移和初速度下的自由振动可归结为如下定解问题

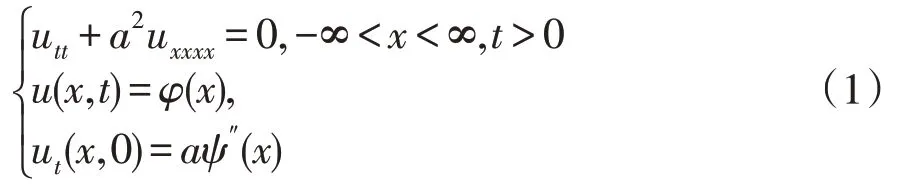
其中φ(x),ψ(x)均为已知函数。

证明问题（1）存在定解。

证明对问题（1）的方程及边界条件作关于变量x的傅里叶变换得

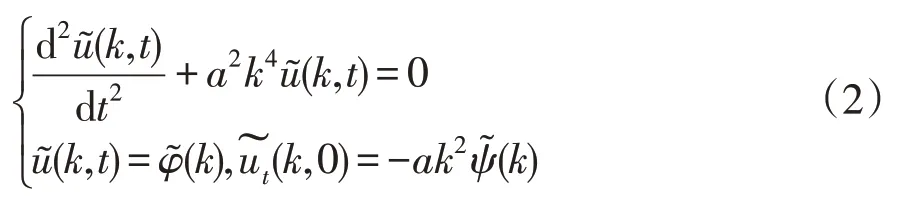
对上式二阶微分方程求通解得

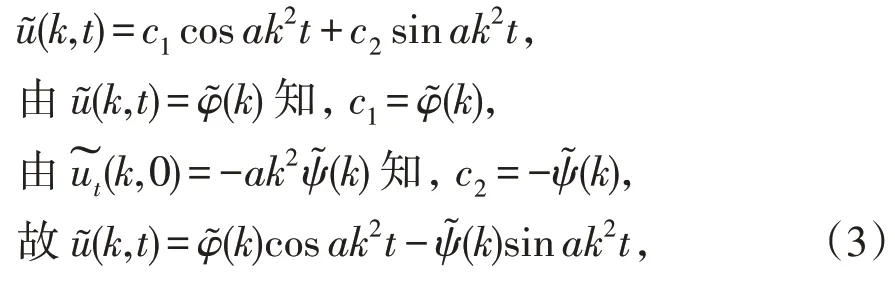
对（3）式进行傅里叶逆变换，有引理1得

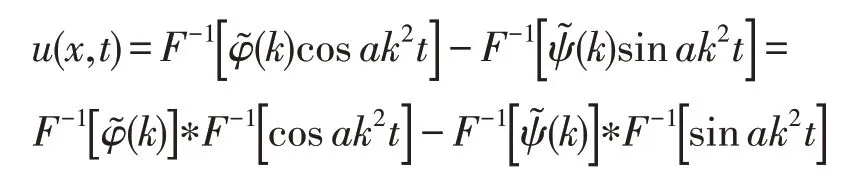
由推论2，可证

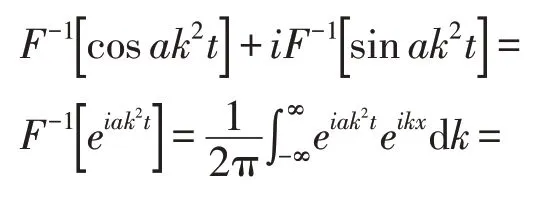
比较两端的实部和虚部，即得

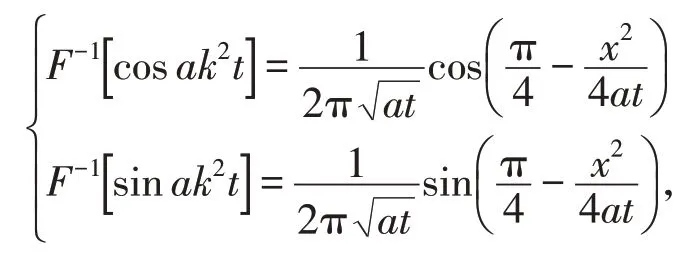
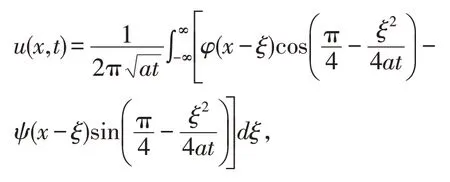
故自由振动方程（1）存在定解。