一类涉及微积分的薄壁圆筒力学问题探索

张艳军

（1.山西大同大学建筑与测绘工程学院，山西大同037003；2.矿山地质灾害防治与环境恢复大同市重点实验室，山西大同 037003）

众所周知，高等数学是近现代科学最重要的数学工具[1],是力学的基础，其在解决力学问题时必不可少，而微积分思想就是一种广泛应用于物理学科的数学思想[2], 研究力学问题时，微元选取和建立模型的方法，是涉及微积分力学问题的很好切入点，运用于教学实践，有利于学生在数学和力学学科间感受知识融通的妙趣[3]。微积分手段和薄壁圆筒力学问题结合求解薄壁圆筒在内压强作用下的径向变形时，很多教科书通常通过微积分和胡克定律相结合的方法来进行求解，很少涉及其他方法，为此，介绍一种解决此类问题的能量法[4]，提供一种借鉴。

1 微积分和胡克定律相结合的求解方法

如图1所示，薄壁圆筒长度b，圆筒壁厚度δ，圆筒半径R，圆筒内压强P，求薄壁圆筒的径向变形Δd。对于这类型题，通常通过微积分和胡克定律相结合的方法来进行求解。

首先，找一个好的切入点，比如微元的选取，如图2所示，在薄壁圆筒上长为dl的圆弧作为微元体，该微元体所对应的圆心角为dθ, 则

在薄壁圆筒上长为dl的圆弧对应微元体的面积为：

该微元体受到的沿着半径方向的力为：

如图2所示。

图2 薄壁圆筒受力分析图

该微元体受到的沿着半径方向的力沿着竖向方向的分力为：

两边积分得

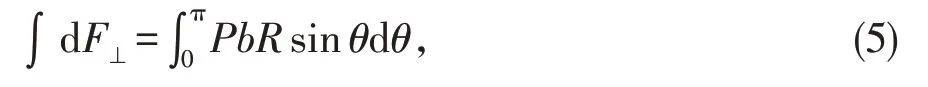
将（1）（2）（3）（4）（5）联立得：

根据平衡关系知：

则有薄壁圆筒的环向轴力为：

（8），（9），（10）联立得：

根据胡克定律可知

根据线应变可知

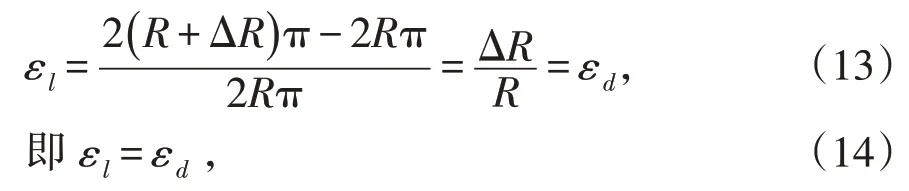
联立（11）（12）（13）(14)式得出薄壁圆筒的径向变形为：

2 能量法

能量法是一种基于功能原理基础之上的方法，通过计算能量，根据功能关系反解其变形。该方法的特点是：简单高效，不易出错。下面介绍能量法计算薄壁圆筒的径向变形。

薄壁圆筒在内压强P的作用下所做的功为：

薄壁圆筒的内压力为：

薄壁圆筒的内面积为：

联立（16）（17）（18）式得：

薄壁圆筒的应变能为：

薄壁圆筒的环向周长为

薄壁圆筒的环向面积为

将（8）（20）（21）（22）联立得：

通过功能关系知：外力对薄壁圆筒所做的功等于薄壁圆筒产生的应变能，可得

联立（19）（23）得：

从以上解题方法可以看出，能量法的优点在于：（1）可以忽略中间过程，只算最终状态；（2）能量是标量，容易计算。

3 结论

（1）两种方法求解结果一致，证明了能量法的正确性；

（2）能量法为薄壁圆筒的径向变形提供一种新的求解方法。