氢原子角动量量子化模型的可视化

张雷 李姝丽 李院院

摘要：量子力学发展史上最突出的成就之一是对氢原子光谱和化学元素周期律给予了相当满意得解释。氢原子理论，通过Schrodinger方程可以严格求解，还是了解复杂原子及分子结构的基础。文章基于Matlab，根据氢原子薛定谔方程的结论，建立角动量空间量子化模型，使抽象的内容形象化，加强物理模型实质讲解、激发学生学习兴趣、提高教学质量具有非常重要的作用。

关键词：氢原子;角动量;量子化;Matlab

中图分类号：G642.41     文献标志码：A     文章编号：1674-9324（2020）12-0322-03

量子力学是反映分子、原子、原子核和基本粒子等微观粒子运动规律的理论，对初学者来说，人们普遍感到量子力学的概念抽象、理论性强、数学难度大、计算烦琐、难以理解，打破了学习普通物理的思维模式，做题时束手无策，学习和掌握该课程的困难很大[1-4]，因此教师教学效果不尽如人意。作为目前最为流行的科技应用软件之一Matlab，不仅具有强大的数值计算能力和功能齐备的可视化能力[5-7]，而且具有编程简单、专业函数丰富的图像处理工具箱，在许多研究领域得到了广泛应用。本文基于Matlab，根据氢原子薛定谔方程的结论，建立角动量空间量子化模型，使抽象的内容形象化，在课堂教学中引入Matlab软件模拟氢原子的角动量的量子化模型，不仅提高学生学习兴趣和教学质量，同时使学生更好地理解量子力学的思想，对教学过程起到了事半功倍的作用[8]。

一、电子和核组成的氢原子体系的薛定谔方程

电子在带正电的核所产生的库仑电场中的运动，选取核的位置作为坐标原点，如果把这些结果直接应用与氢原子，则只有当原子核是固定的时候，才是完全准确的，严格意义上，在研究氢原子问题中，应该考虑核的运动，考虑两个粒子（电子和核）在库仑相互作用下的运动，这是一个两体问题的研究，在经典力学中，我们研究两体问题可以归结为一个粒子在场中的运动，而在量子力学研究中，情况也应该是这样[9]。

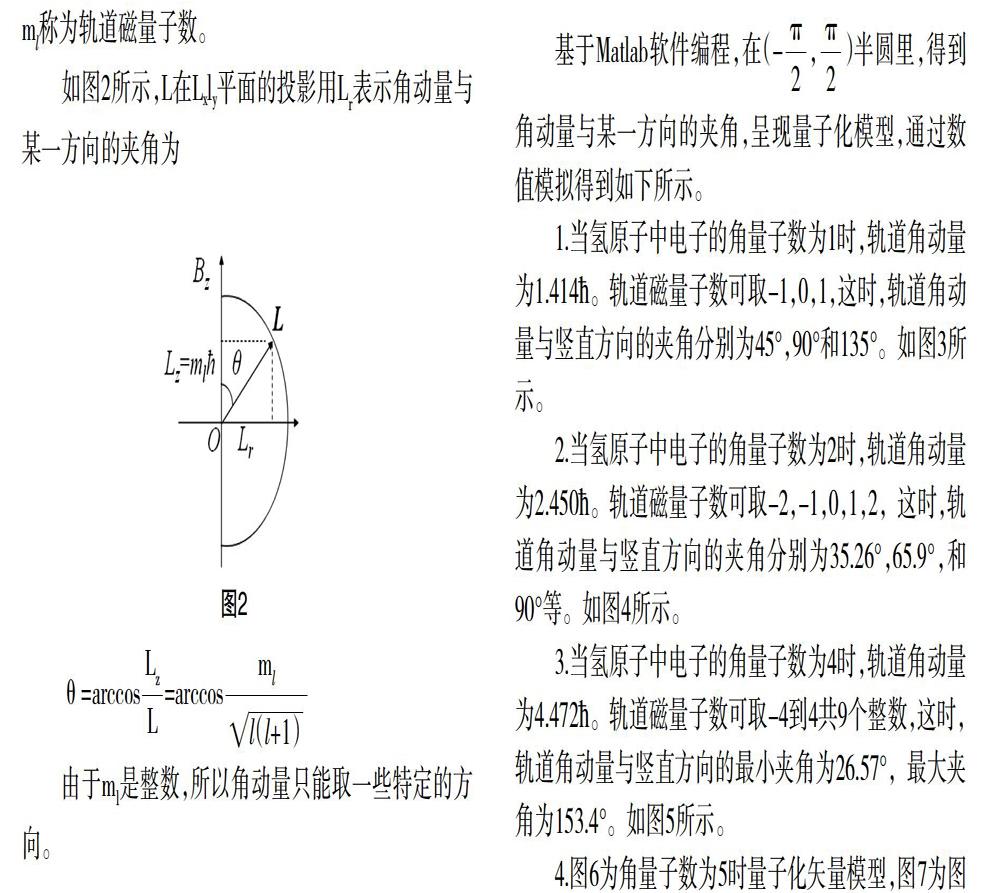
氢原子核外电子的角动量在空间任意方向（如外磁场方向）的投影也是不连续的，只能取一些特殊的不连续的值。即：角动量在空间任一方向的投影也是量子化的，这种现象称为角动量空间量子化。

三、基于matlab的可视化

角动量是原子、分子以及基本粒子物理研究中的重要物理量，它在理论研究和应用研究中都有重要意义。量子力学教学实践中，学生常常感到角动量概念学习比较困难。在量子力学中，角动量的三个空间分量取值都是量子化的，并且角动量矢量一般不能有确定值，但它在空间某一轴上的投影可以有确定的值。对于确定的l，m只能取0，±1，±2，…，±l共2l+1个值，m称为轨道磁量子数。

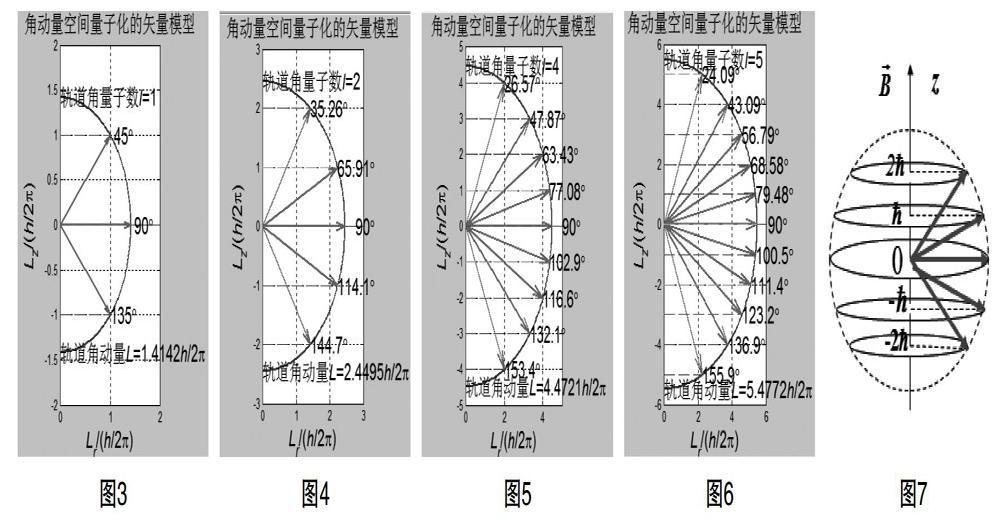
1.当氢原子中电子的角量子数为1时，轨道角动量为1.414？捩。轨道磁量子数可取-1，0，1，这时，轨道角动量与竖直方向的夹角分别为45°，90°和135°。如图3所示。

2.当氢原子中电子的角量子数为2时，轨道角动量为2.450？捩。轨道磁量子数可取-2，-1，0，1，2，这时，轨道角动量与竖直方向的夹角分别为35.26°，65.9°，和90°等。如图4所示。

3.当氢原子中电子的角量子数为4时，轨道角动量为4.472？捩。轨道磁量子数可取-4到4共9个整数，这时，轨道角动量与竖直方向的最小夹角为26.57°，最大夹角为153.4°。如图5所示。

4.图6为角量子数为5时量子化矢量模型，图7为图4对应的立体图像。

四、结语

针对学生在量子力学课程学习中困惑，以角动量的量子化为例，通过引入MATLAB软件进行绘图和数值计算，明确角动量在空间的量子化模型，从而使复杂的内容得以简化，同时也使抽象难懂的内容得以形象化，强化物理实质讲解，同时还能够更好地调动学生学习量子力学的积极性，有效提高量子力学的教学质量。

参考文獻：

[1]刘萍云，邹晓蓉.量子力学教学探讨[J].高等教育研究学报，2006，29（1）：67-69.

[2]顾锦华，陆轴，康淮.钼掺杂氧化锌薄膜的制备及其性能研究[J].中南民族大学学报（自然科学版），2017，36（2）：66-72.

[3]魏群.量子力学教学中的数学问题[J].新疆石油教育学院学报，2004，7（7）：85-86.

[4]钟志有，康淮，陆轴，等.掺镁氧化锌薄膜结构及其光学性质的研究[J].中南民族大学学报（自然科学版），2017，36（1）：64-70.

[5]顾锦华，钟志有，王皓宁，等.《大学物理实验》中的数据处理方法研究[J].（绿色科技），2018，（15）：275-276.

[6]钟志有，康淮，龙浩.镁钇合掺氧化锌薄膜的制备及其性能研究[J].中南民族大学学报（自然科学版），2018，37（1）：66-72.

[7]张笑天，杨奋强.MATLAB7.基础教程[M].西安：西安电子科技大学出版社，2008，46-49.

[8]钟志有，龙浩.MATLAB软件在量子力学教学中的应用[J].绿色科技，2019，（1）：223-224.

[9]周世勋.量子力学教程[M].2版.北京：高等教育出版社，2009.

[10]周世勋.量子力学教程[M].2版.北京：高等教育出版社，2009.