角动量算符的本征值

高　峰，许成科，张登玉，游开明

（1.衡阳师范学院物理与电子工程学院，湖南衡阳 421002；2.衡阳师范学院南岳学院，湖南衡阳 421008）

角动量算符的本征值

高峰1，2，许成科1，2，张登玉1，2，游开明1

（1.衡阳师范学院物理与电子工程学院，湖南衡阳 421002；2.衡阳师范学院南岳学院，湖南衡阳 421008）

量子物理学中，角动量算符是一个十分重要的物理量，可以用它的本征值来表征微观体系的状态。本文根据对易关系，利用较为简便的方法求出任意角动量算符的本征值，并讨论了轨道角动量算符和自旋角动量算符的本征值。

角动量算符；对易关系；本征值

0　引言

角动量是物理体系的一个重要物理量，它是确定体系状态的物理量之一。特别是在研究原子问题时，它显得尤为重要，根据原子体系角动量的取值可以确定其状态。原则上，量子力学可以根据最基本的转动求出角动量算符。量子力学的一个十分重要的任务就是求解力学量算符的本征方程，从而得出算符的本征值和本征态。

相对于宏观系统而言，微观体系要复杂得多，其角动量除轨道角动量之外，还有自旋角动量。自旋是微观体系特有的物理现象，不存在经典类比，尽管地球除绕太阳旋转以外也还有自转，但这种自转归根结底还是一种轨道运动。人们经过研究发现，对于任意的转动，无论是轨道角动量、自旋角动量，还是总角动量、分角动量，其相应的角动量算符都具有一些共同的特点。例如，任意一种角动量算符^J都满足如下对易关系

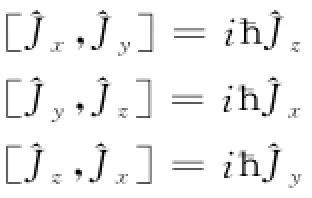
简记为

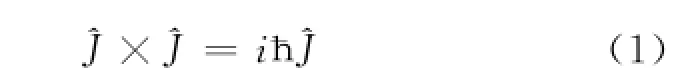
这是角动量算符最重要的性质，它也可直接作为角动量算符的定义［1］［2］。

一般说来，要想得到力学量算符的本征值和本征态，需要求解该算符的本征方程。而求解微分方程并不是一件容易的事情，特别是求解那些较复杂的算符的本征方程，就更加困难了，有些本征方程根本无法精确求解。本文根据角动量算符的对易关系，直接求出任意角动量平方算符^J2及角动量Z分量算符的本征值，并具体讨论了轨道角动量算符和自旋角动量算符的本征值。

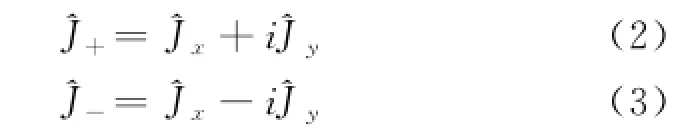
有学者称它们为阶梯算符，也有称它们为上升、下降算符［3］。将上两式相乘，有

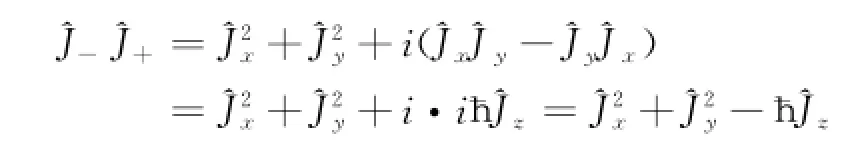
得

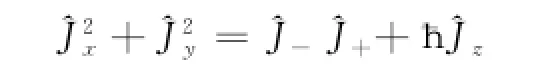
于是有

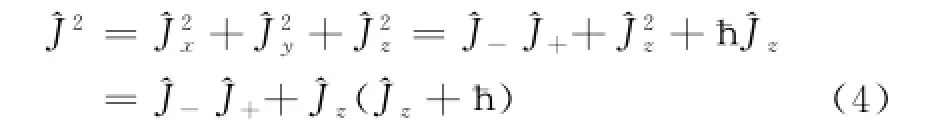
同理可得

很容易证明这些算符存在如下对易关系

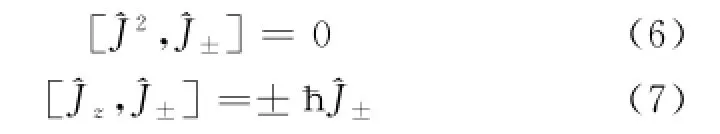
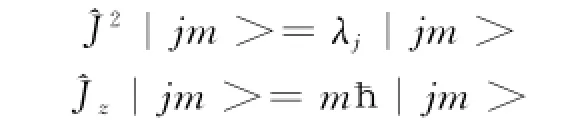
根据（6）式，得

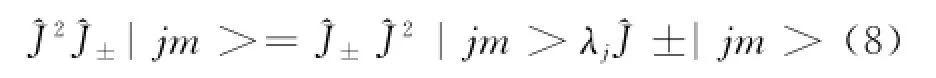
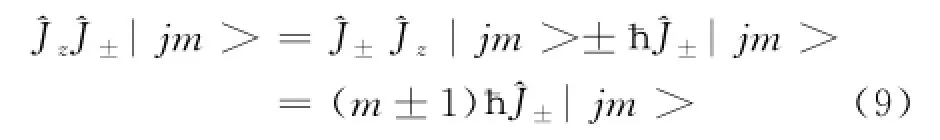
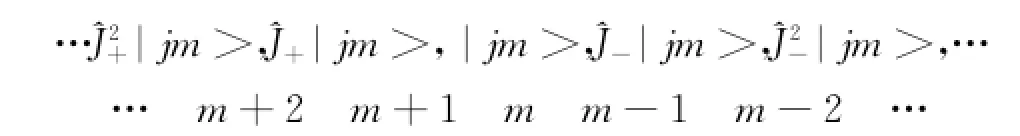
为了证明此序列两端必有终结之时，先计算^J2在| jm＞中的平均值。

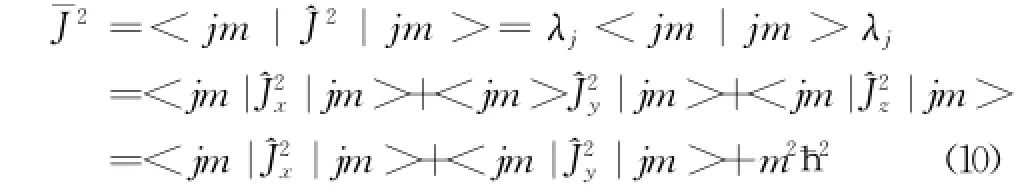
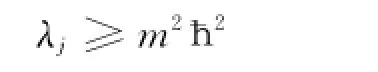
因此只要λj有限，m就必有上界；另一方面m2为正，|-m|不可能大于上限m，则m就必有下界。设m的最大值和最小值分别为mmax和mmin，则必有

于是有

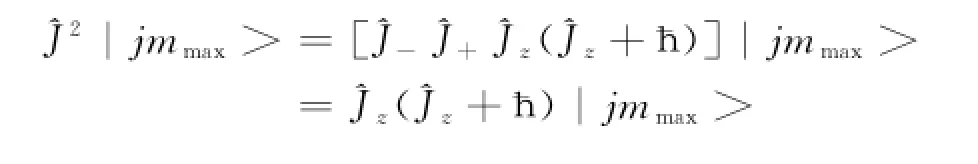
即

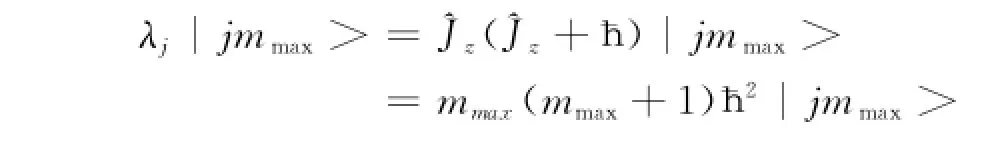
另一方面，根据（5）式，又有

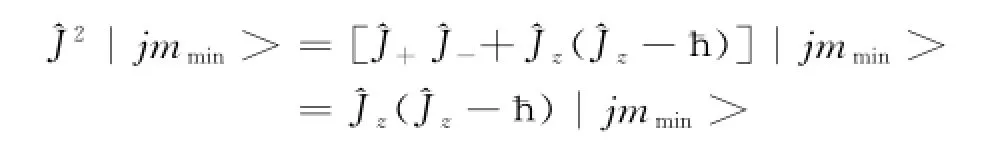
即

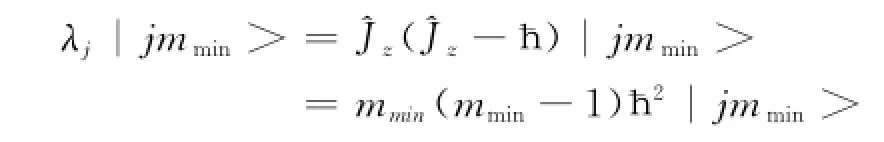
所以有

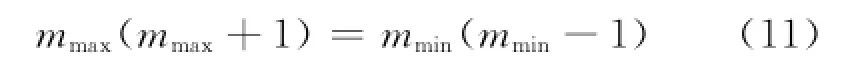
注意到mmax＞mmin，方程（11）的唯一解为

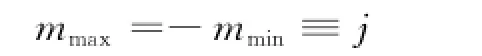
于是得出^J2的本征值为

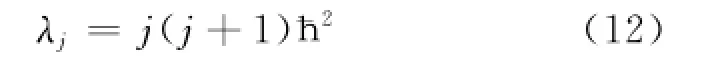
此外，由于（mmax-mmin）必为整数，故j只能取整数或半整数。显然m的取值为

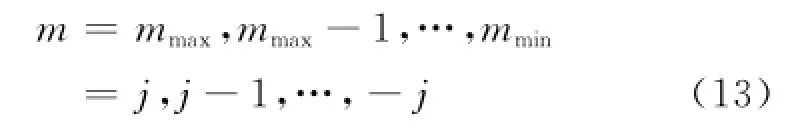
故得到^Jz的本征值为

2　轨道角动量算符及自旋角动量算符的本征值

（12）式和（14）式是计算角动量算符及角动量Z分量算符本征值的一般表达式，不管是轨道角动量算符还是自旋角动量算符，也无论是分角动量算符还是总角动量算符，其本征值都可以表示成（12）式和（14）式的形式。若要具体算出本征值的大小，就必须知道相应的量子数。对于轨道角动量算符^L，由（12）式得其本征值为

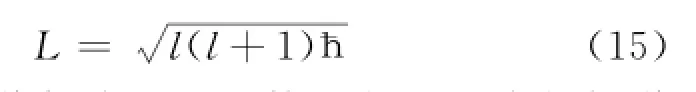
上式中L为轨道角动量量子数。由（14）式得轨道角动量Z分量算符的本征值为

其中ml称为投影量子数或磁量子数，且

对于自旋角动量算符，由于自旋角动量是微观体系内部状态的表征，没有相应的经典表达式，不象其它力学量那样可以表示为坐标和动量的函数，故不能采用^r和^p来得到自旋角动量算符，因此情况要复杂一些。现以电子为例，讨论自旋角动量算符^S的本征值。大量实验事实说明电子的自旋角动量在任何方向上的投影只能取两个数值（±ħ/ 2），在x、y、z方向上的投影当然也一样，于是，力学量Sx、Sy、Sz的可能值，也即的本征值都为（±ħ/2）。所以有

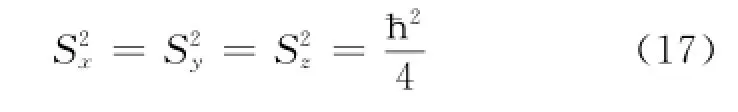
自旋角动量平方算符的本征值为

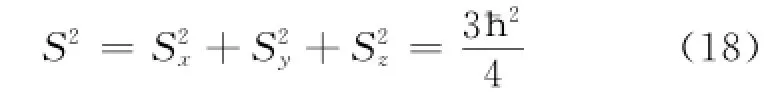
根据（12）式，电子的自旋角动量算符的本征值可表示为

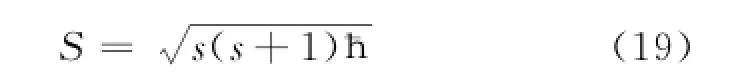
式中s称为自旋角动量量子数，结合（18）式和（19）式得到电子的自旋角动量算符的本征值为，还可以得出电子的自旋角动量量子数为

3　结束语

量子力学的核心问题就是要解决体系状态随时间的演化规律［4］，解决该问题可以有两条途径：一是态函数随时间的演化，二是算符随时间的演化。在量子力学中，所有的力学量都必须要用算符来表示，因此，算符理论在量子力学中占有十分重要的地位［5］。角动量算符的本征值可以用于表征体系的状态，所以本文专门讨论了角动量算符的本征值问题。对于初学量子力学的读者而言，角动量算符理论既抽象又难以掌握，主要原因是因为内容较多，没有把握其特点和规律。通过上面的讨论容易看到，任何一种角动量算符及其分量算符的本征值都可以写成（12）式和（14）式的形式，只要抓住了这一点，问题就变得简单了。

［1］邹鹏程.量子力学［M］.北京：高等教育出版社，2003.

［2］高峰.量子物理学［M］.上海：华东师范大学出版社，2015.

［3］林辛未.轨道角动量算符的本征值得和本征函数与阶梯算符［J］.大学物理，1985，4（9）：27-29.

［4］高峰，周娟娟，张登玉，等.关于氢原子体系Schrodinger方程的讨论［J］.衡阳师范学院学报，2010，31（6）：27-30.

［5］高峰，张登玉，张军民，等.两个力学量算符具有共同本征态系的条件［J］.大学物理，2009，28（11）：18-20.

The Eigen Value of Angular Momentum Operator

GAO Feng1，2，XU Cheng-ke1，2，ZHANG Deng-yu1，2，YOU Kai-ming1
（1.College of Physics and Electronic Engineering，Hengyang Normal University，Hengyang Hunan 421002，China；2.Nanyue College of Hengyang Normal University，Hengyang Hunan 421008，China）

The angular momentum operator is a very important physical quantity in quantum physics，and we can use it to represent the micro system of the state.In this paper，the simple method is used to calculate the angular momentum of the Eigen value of the operator according to the commutation relation，and the Eigen value of the orbital angular momentum operator and the spin angular momentum operator is discussed.

angular momentum operator；commutation relation；Eigen value

O413.1

A

1673-0313（2015）06-0043-03

2015-06-22

教育部第一类特色专业建设点项目（TS11635）；湖南省教育厅2010年普通高校教改项目（297）；湖南省普通高校光电课程组教学团队（2011）项目；衡阳师范学院2008年精品课程建设项目（06）；湖南省教育厅普通高校教改项目（湘教通［2012］401号）332

高峰（1960-），男，湖南衡阳人，教授，主要从事量子物理、核科学与技术的教学和研究。