无线光通信中喷泉码的发展现状与展望

吴 一，刘宏展，郝 源，刘丽媛

无线光通信中喷泉码的发展现状与展望

吴 一，刘宏展*，郝 源，刘丽媛

华南师范大学信息光电子科技学院，广东省微纳光子功能材料与器件重点实验室，广东 广州 510006

无线光通信信道复杂多变，喷泉码作为一种新兴的无速率编码无需信道的先验信息即可实现不同信道环境下的自适应传输，与传统编码相比更能提升无线传输的质量。本文首先总结了喷泉码应用于无线光通信的优势以及国内外喷泉码的发展现状，然后深入研究了两类喷泉码编码方案的设计以及对喷泉码性能影响重大的度分布函数的设计，总结了一种喷泉码即(LT)码的译码方法以及近些年不断提出优化的方案，同时指出了喷泉码设计中亟需解决的关键难点，最后提出了喷泉码应用于无线光通信的必要技术和探索方向。

无线光通信；喷泉码；无速率编码；度分布函数

1 引 言

无线光通信(Optical wireless communication，OWC)是一种新兴的视距传输技术，与传统射频(radio frequency，RF)通信相比，具有保密性好、带宽高、信道容量大以及无需频率请求等优点。但是，由于激光信号在大气中传输易受到大气湍流等效应的影响，易产生光束漂移，强度起伏等问题，使得无线光通信中光束传输质量降低，严重影响了OWC系统的性能[1]。

无线光通信信道复杂多变，受天气、海拔等条件影响较大，传统的线性分组码、卷积码、极化码等编码方法往往采用事先确定好的码率传输，在受到信道条件不规律变化的影响时，会使得译码端复杂度高，并造成较高的误码率和通信时延；并且，在大气条件较好时，若采用较低的发射功率与较低码率编码方案，又会影响通信效率，使其无法充分利用无线光通信中丰富的信道资源[2]，考虑到喷泉码的诸多特性，将其应用于无线光通信具有一定的研究意义。

喷泉码最初在解决大规模数据可靠性传输和广播或者多播快速传输的问题中被提出。与传统信道编码相比，喷泉码由于其码率不固定的特性更加适合无线光通信[3]，其本身可以利用信道估计和译码端信噪比估计等算法，估计大气信道的衰落特性，然后利用喷泉码的译码累积分布函数动态调整码率和发射机发射功率，根据信道的变化自动改变编码方式，用来提高无线光通信的有效性，甚至在信道反馈或者信道估计不准确时也能一定程度上保证通信质量。喷泉码具有广阔的应用前景，目前已被DVB-H和3GPP TS等国际标准采用[4]。

本文介绍了喷泉码的优势以及目前国内外发展现状，综述了已经提出的两类实用喷泉码的度分布函数的设计以及不同的译码方案，归纳了前人对喷泉码性能不断优化的方案，同时指出了喷泉码应用于无线光通信中需要解决的一些关键问题，最后对喷泉码在无线光通信领域的发展前景和研究方向进行了展望。

2 喷泉码的优势和发展现状

传统的前向纠错(forward error correction，FEC)方式需要预先估计信道状态信息，并根据实际情况选择合适的编码长度及码字，通常在OWC系统中，信道质量因为天气的变化区别较大，故需要多次重复设计编码方案，这样大大增加了系统的复杂度[5]。

除此之外，无线通信下大规模MIMO(multiple input multiple output)系统可以引入喷泉码，不同的接收端可以根据处理能力和信道条件自主选择接收合适数量的编码包，一旦完全恢复了原始信息就停止接收，不同接收端不会相互影响，有效地降低了MIMO系统的复杂度。喷泉编码器产生的不同编码数据包之间相互独立且完全等价，能否译码成功仅仅取决于接收到编码包的数量，与接收到编码包种类和顺序无关[6]。由于无线光通信系统在恶劣天气条件下通常会通信中断，利用喷泉码的特性，在接收端叠加累积译码，可以在高中断概率的条件下得到比较好的效果，也可以有效解决断点续传和异步接入带来的复杂度问题。而且一旦成功译码，接收端只需给发送端一个反馈信号，从而避免了传统线性分组码的复杂反馈过程带来的“反馈风暴”问题[7]。

基于以上优势，喷泉码在被提出后的二十多年来受到了广泛的关注[8]。目前的研究主要集中于编码方式的选择[9]、度分布的设计与优化、译码算法的设计、与具有高纠错能力的编码级联[10-12]、利用不等差错理论[13]实现高质量传输以及喷泉码理论在数据传输，深空通信和云存储等场景的实际应用拓展[14]。

表1介绍了喷泉码的研究现状。在国内的研究中，2017年，重庆理工大学的张勋课题组研究了在2´2的MIMO_FSO系统中，用Gamma-Gamma模型模拟大气湍流信道下基于修正转移鲁棒孤子度分布(ISRSD)[15]的LT码与传统LDPC码的性能比较。使用改进的LT码能够在强湍流条件下，误码率为10-6时获得2.2 dB的编码增益，同样误码率情况下，在弱湍流条件下获得0.9 dB的编码增益。随后，又研究了鲁棒泊松度分布(PRSD)下的LT码在3´3 MIMO-FSO的性能。在强湍流条件下，误码率为10-6时，采用PRSD度分布的LT码比RSD获得了1 dB的编码增益；弱湍流条件下，同样误码率下，采用PRSD的LT码比RSD获得了0.4 dB的编码增益。以上成果研究了喷泉码及其改进方案，对优化无线光通信质量大有裨益[15]。

3 喷泉码的原理与分类

喷泉码可以形象地表示为图1，这里编码器为一个喷泉源，喷泉源向外面随机地喷洒水珠(编码包)，接收水桶即为译码器，目的是接到足够的水(完成译码)。“水桶”不关心水从哪里来，如果某次检查发现水不够(译码失败)，则继续接水珠(编码包)，直到解渴(完成译码)[25-27]。

图2介绍了上述喷泉码编码器和译码器的原理，首先编码器对数据进行分割，进行异或操作得到源源不断的数据包；然后译码器接收到编码器产生的源源不断的数据包，对数据包进行处理恢复出原始数据[28]。

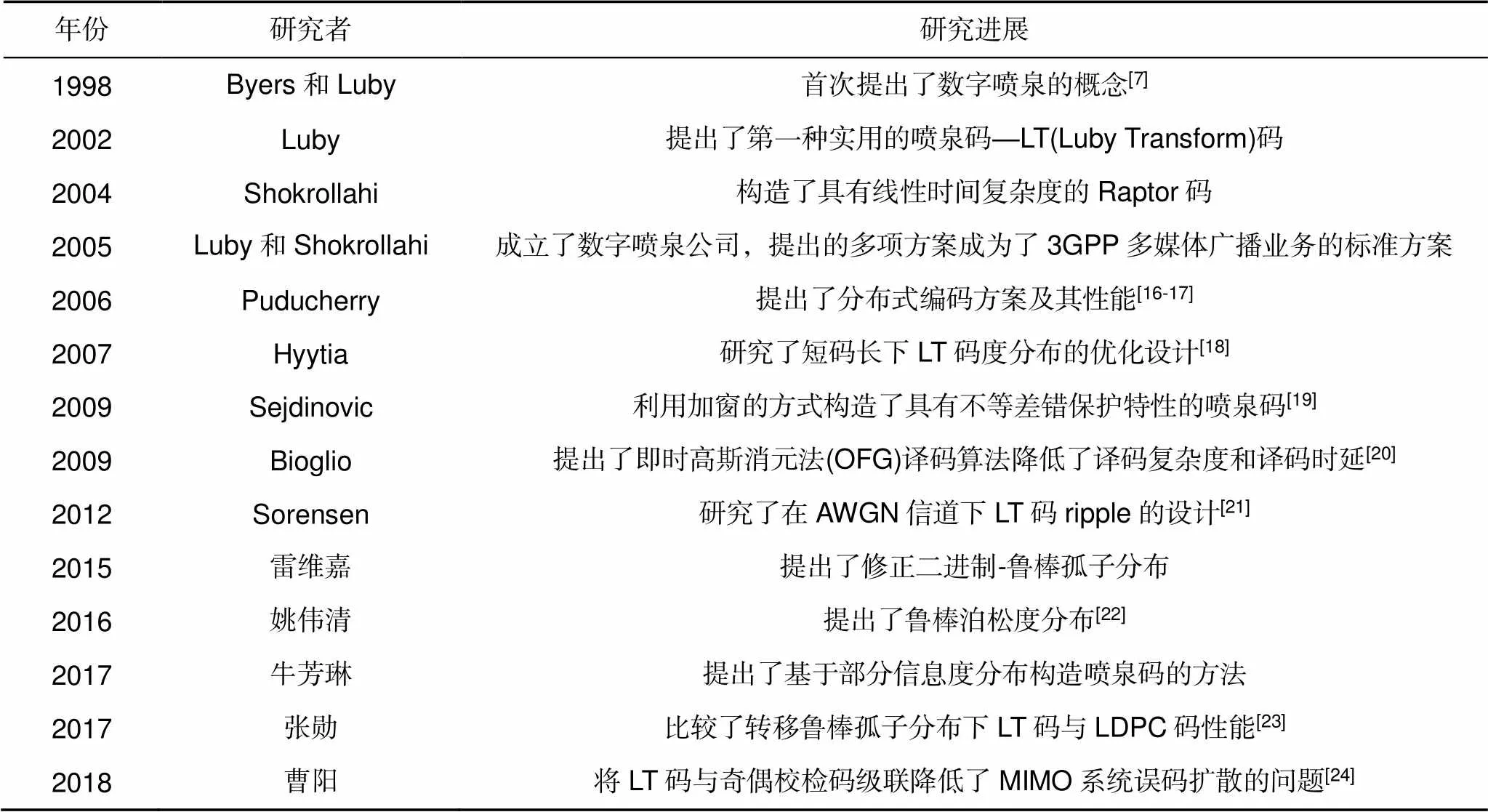
表1 国内外喷泉码的研究进展

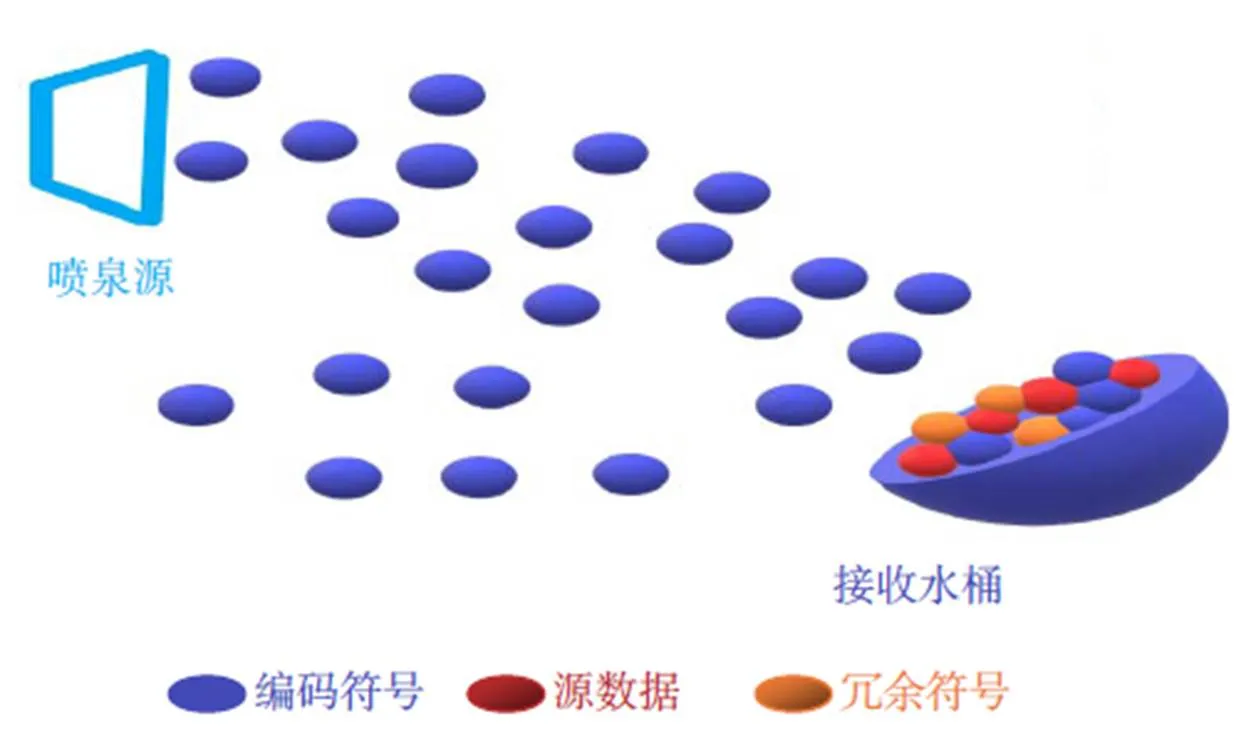
图1 喷泉码原理示意图

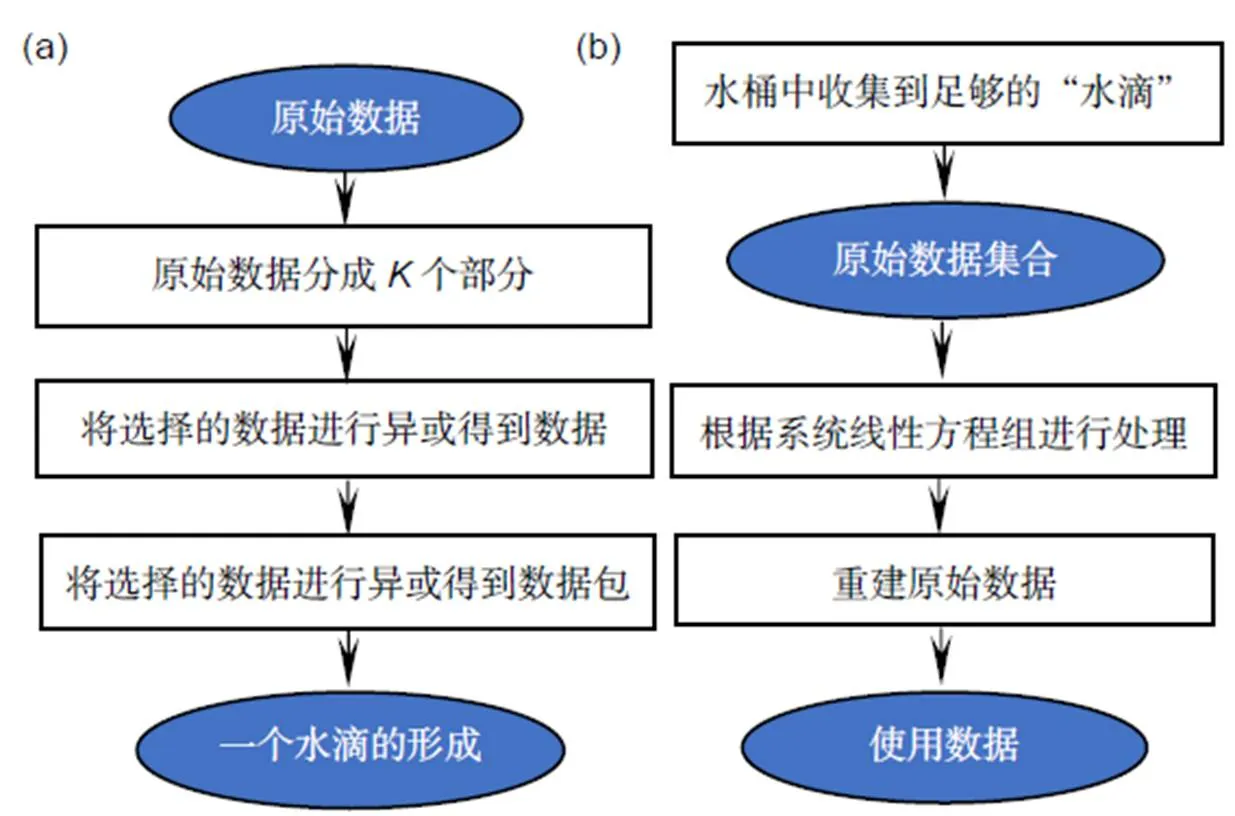
图2 (a) 喷泉码的编码器原理；(b) 喷泉码的译码器原理

从理论上来看，喷泉码的编码器和译码器仍有一些细节需要考虑：

编码器：1) 需要预先设定相应的函数来保证所有的数据包都能被选择，而不会有遗漏导致译码失败；2) 在保证喷泉码译码端能译码成功条件下，译码端所需要的编码分组尽可能小，编码数据包应该尽可能简单，减少译码器的工作负担[29]。

译码器：译码器选择的译码算法应该能从任意一组(>)个编码数据包中恢复个原始数据。接近即意味着译码开销很低，而且译码器的复杂度能够与个原始数据有线性关系，这就是比较优良的译码器。

根据以上讨论，目前有两类受到广泛研究的喷泉码，即LT码和Raptor码。

3.1 LT码

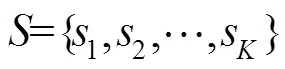
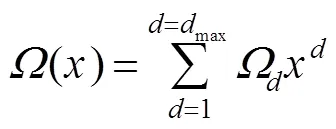
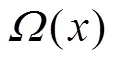
如图3，LT码的编码过程：1) 根据预先选定的度分布函数随机选择一个度值；2) 从个原始信息符号中随机选择个符号进行异或得到一个编码符号；3) 不断根据上述方法源源不断地产生编码符号。

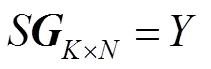
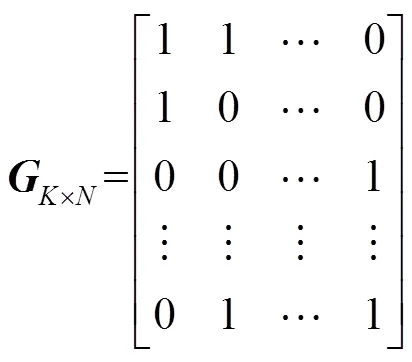
式(2)的编码矩阵取决于度分布函数，度分布函数对LT码的编译码复杂度、错误平层和译码开销等有重要影响[31]。早期提出的线性喷泉码由于采用了均匀分布的度函数，编码符号的平均度值很高使其有较高的编译码复杂度，故这类喷泉码并不实用。所以设计出的一个好的度函数既要保证较低的编译码复杂度，还要实现在接收到比较少的编码符号时就可以开始译码，而且在译码迭代的过程可以持续进行，不至于找不到度值为1的编码符号而译码中断[32-33]。

为了在译码迭代过程中能源源不断找到度值为1的编码数据包，同时平均度值不会明显增加。Luby在理想孤波分布基础上进行了一定的修正，提出了鲁棒孤子分布(robust soliton distribution，RSD)：

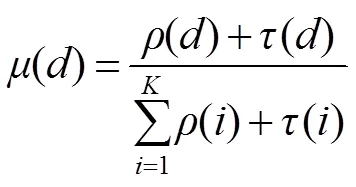
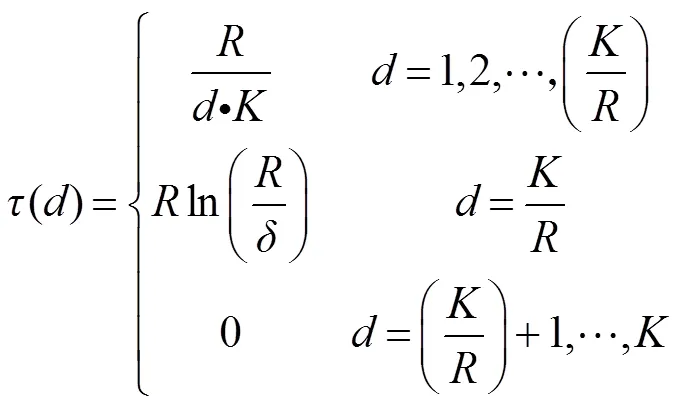
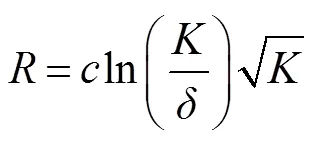
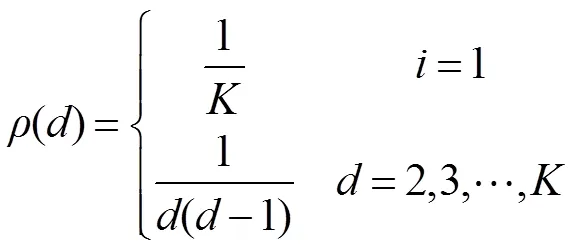
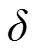
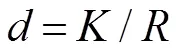
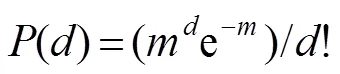
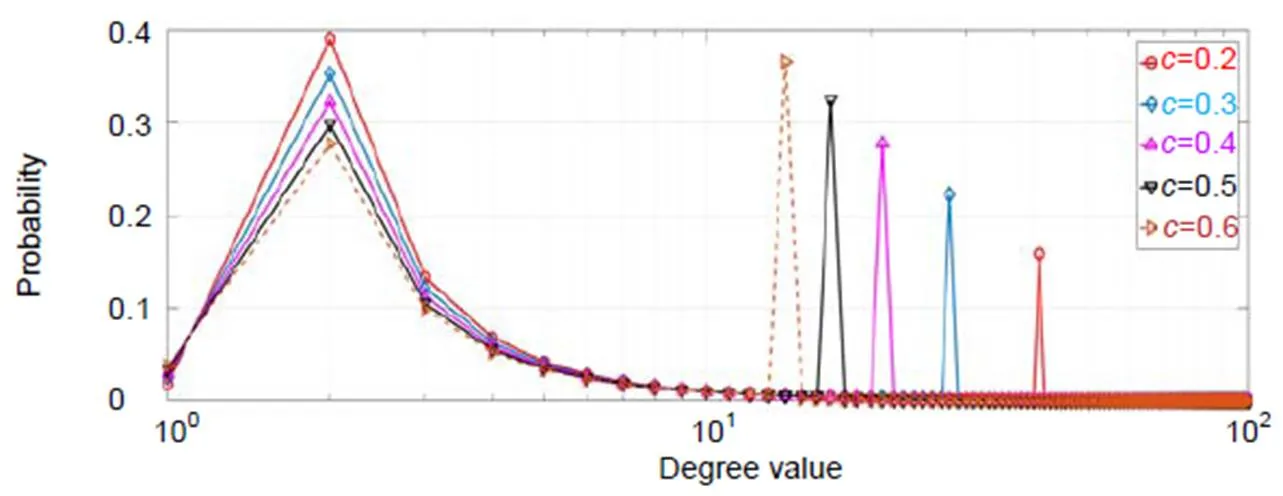
图4 K=10000，δ=0.05，c=0.2，0.3，0.4，0.5，0.6时RSD的概率密度分布

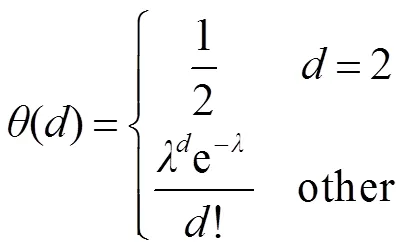
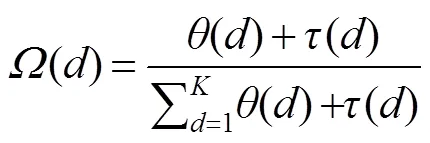
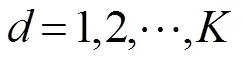
表2比较了优化的PRSD和RSD的性能。

3.2 Raptor码

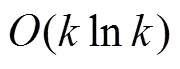
编码过程：1) LDPC码编码：将个原始符号进行LDPC码编码，编为码长为的LDPC码码字，即预编码过程；2) LT码编码：将上述过程产生的LDPC码编码码字作为LT码的输入符号进行LT码编码，产生的LT编码输出符号即为Raptor码的编码符号。

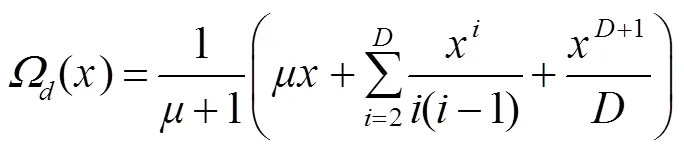
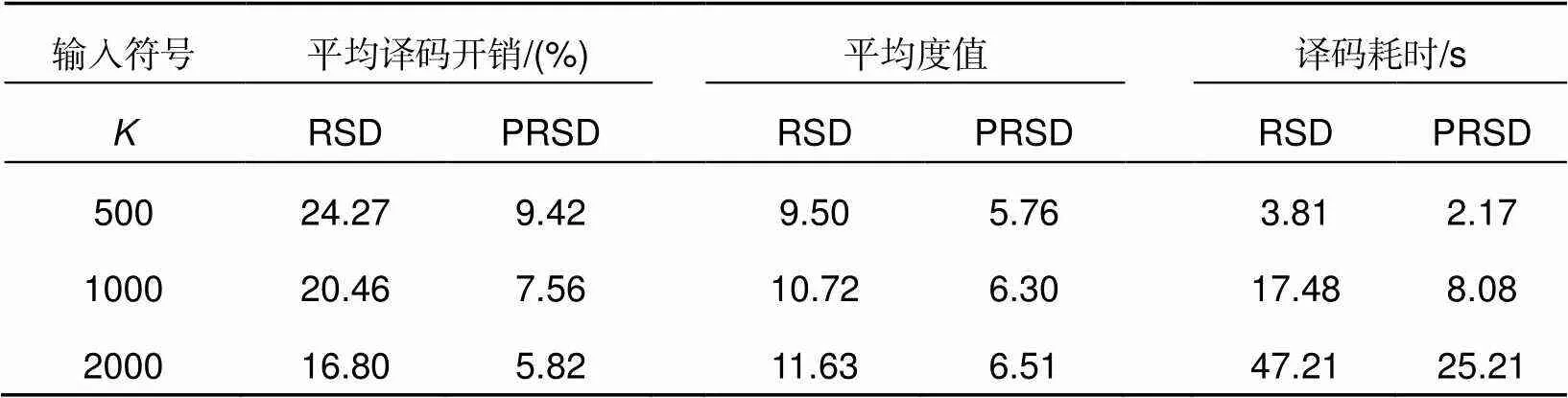
表2 PRSD和RSD的性能对比

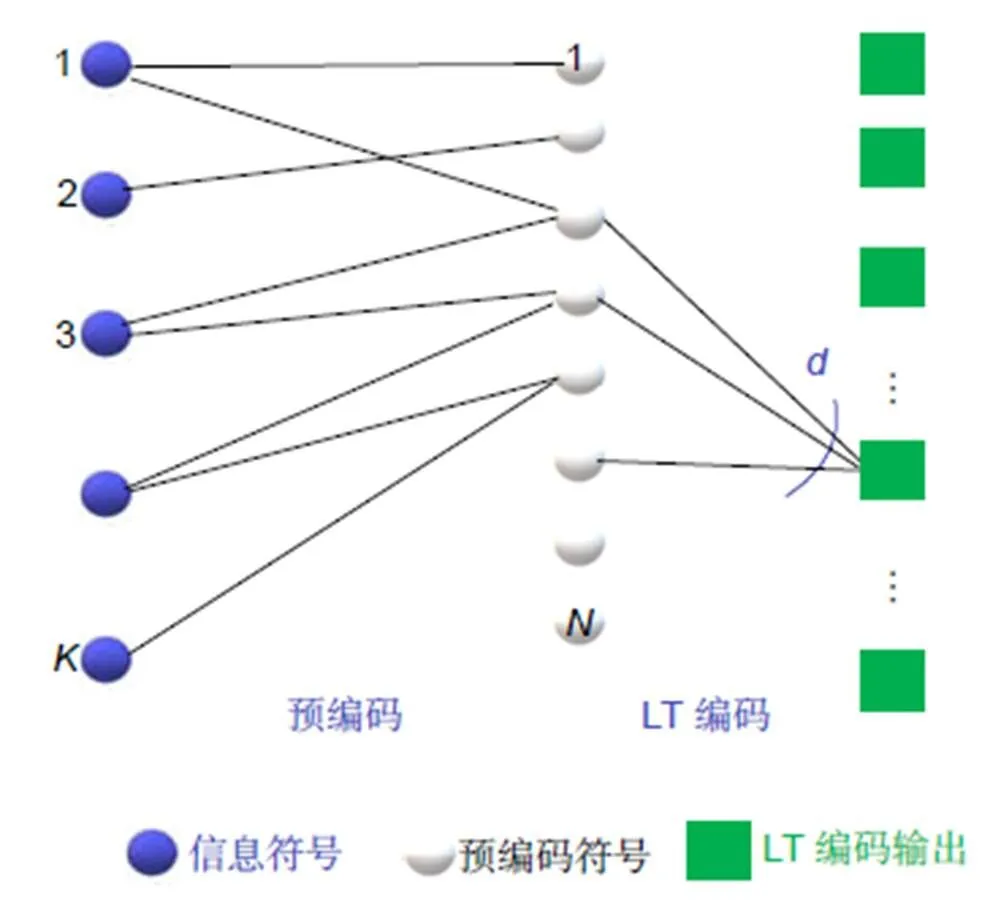
图 5 Raptor的编码过程

Shokrollahi结合了码长来考虑了度分布的设计，得到了Raptor码在有限码长下的度分布设计准则，如表3所示。

其中以码长=65536为例：

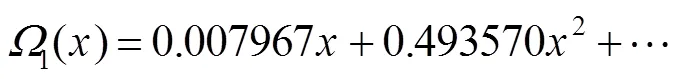
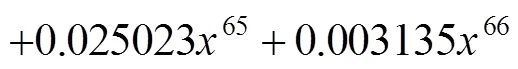
Raptor码与LT码相比拥有线性时间复杂度，并且其错误平层很低可以对信息进行较好的保护非常适合于在复杂差错环境下传输数据。目前，有两类Raptor码被广泛应用和研究，即R10(Raptor10)码和RQ(RaptorQ)码。R10码已经被多个国际化标准组织使用，如3GPP(3rdGeneration Partnership Project)，DVB-H(Digital Video Broadcasting-Handheld)和IETF(Internet Engineering Task Force)。作为FEC的传输方案，R10码适合于中等长度数据块，应用于移动广播等对数据保护要求不高的场合，RQ码适合于目前无线光通信等复杂环境的大规模数据传输且需要较高精确度的场合。

3.3 喷泉码的译码

3.2中介绍的Raptor码是LDPC码和LT码级联得到的，故译码过程为先对LT码进行译码再进行LDPC码译码。故这里着重介绍LT码在BEC信道和AWGN信道下的译码方法[35]。

3.3.1 LT码在二进制删除信道下的BP译码

1) 在编码符号集中寻找一个度为1的编码符号y，假设在二分图上编码符号y与原始符号s相连；

2) 直接令s=y，并在二分图上一出s与y相连的边；

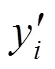
4) 重复上述步骤，直到原始符号被全部译出，或者在迭代的过程中找不到度为1的编码符号。

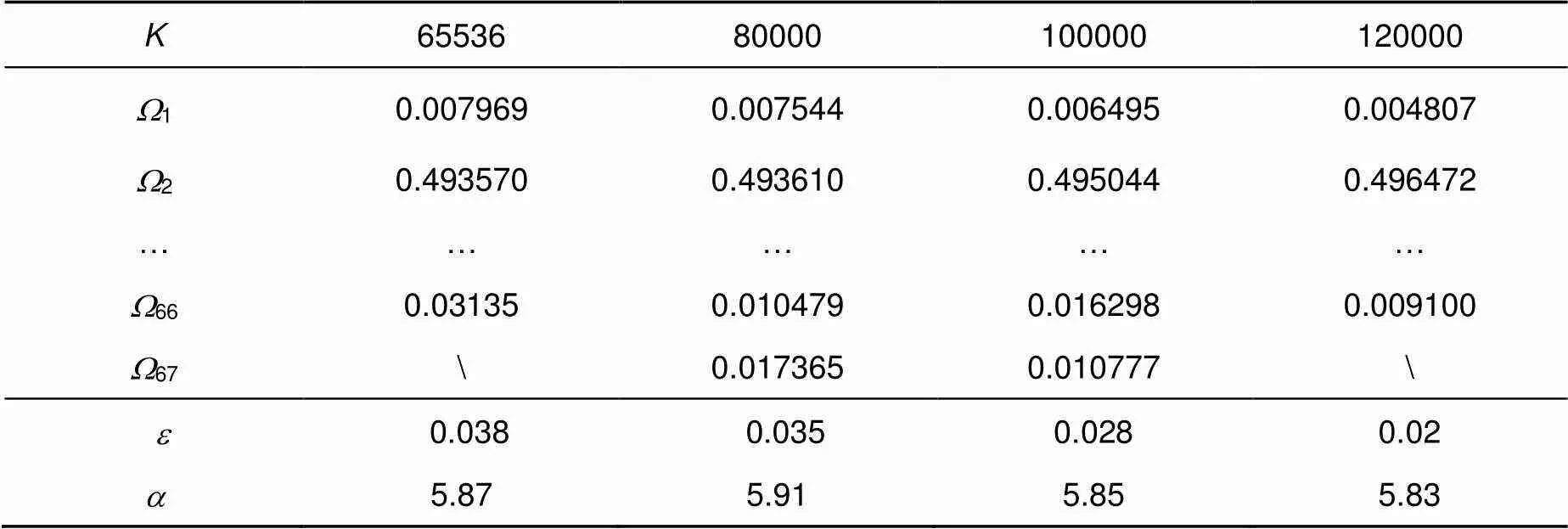
表3 不同码长下优化出Raptor码的度分布

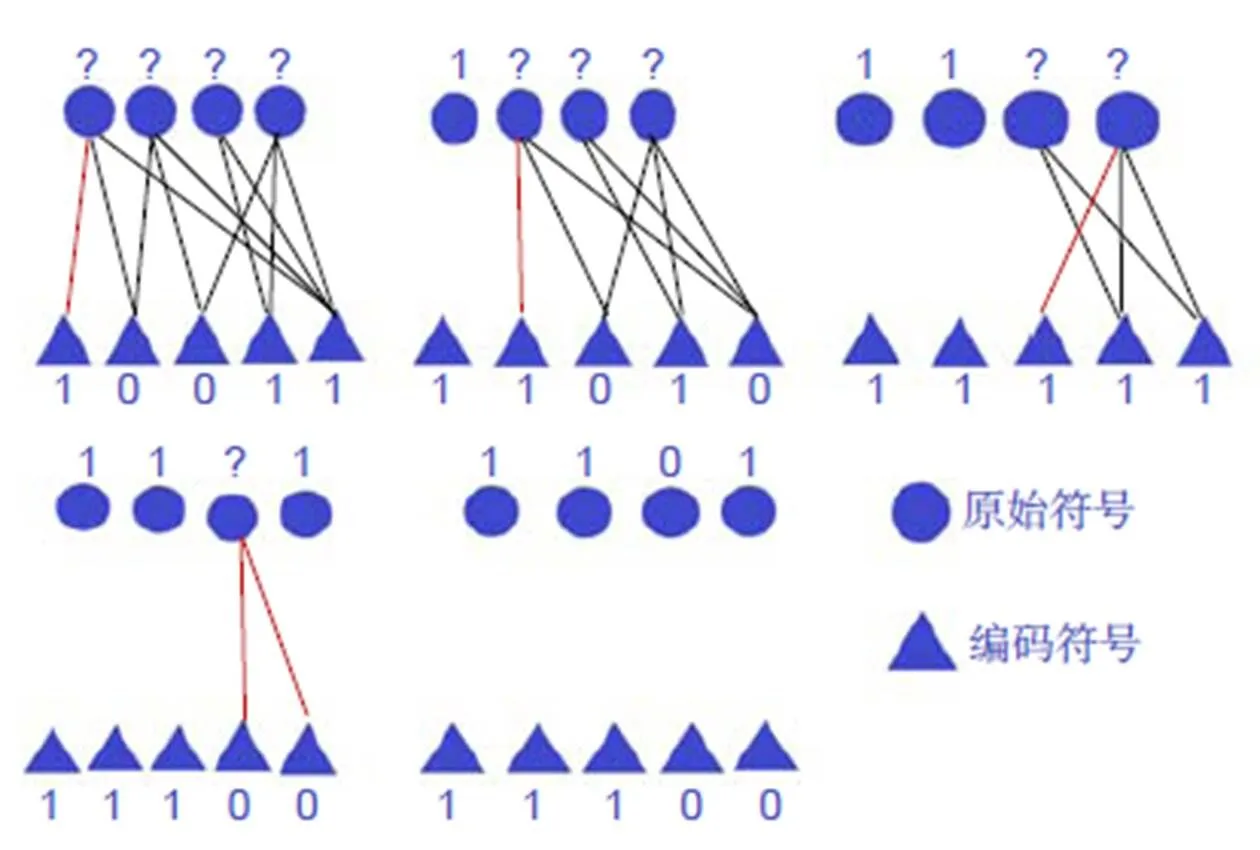
图6 LT码的BP译码方法

2012年Chong等人提出了一种设计简单的短消息喷泉码(short message fountain codes)，能够在理想的信道下，到删除率为0.5的删除信道下以较低的效率成功译码。Huang等人研究了带有消息传递(message passing，MP)和最大似然(maximum likelihood，ML)解码算法的喷泉码在删除信道下的性能，证明了MP算法能够在中长码长下有较高的译码效率，对于短码长MP算法会带来较大的译码开销，在此基础上提出了针对于短码长消息的混合消息传递和快速最大似然译码方法。

3.3.2 高斯消元法译码

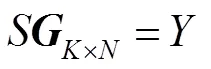
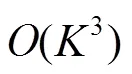
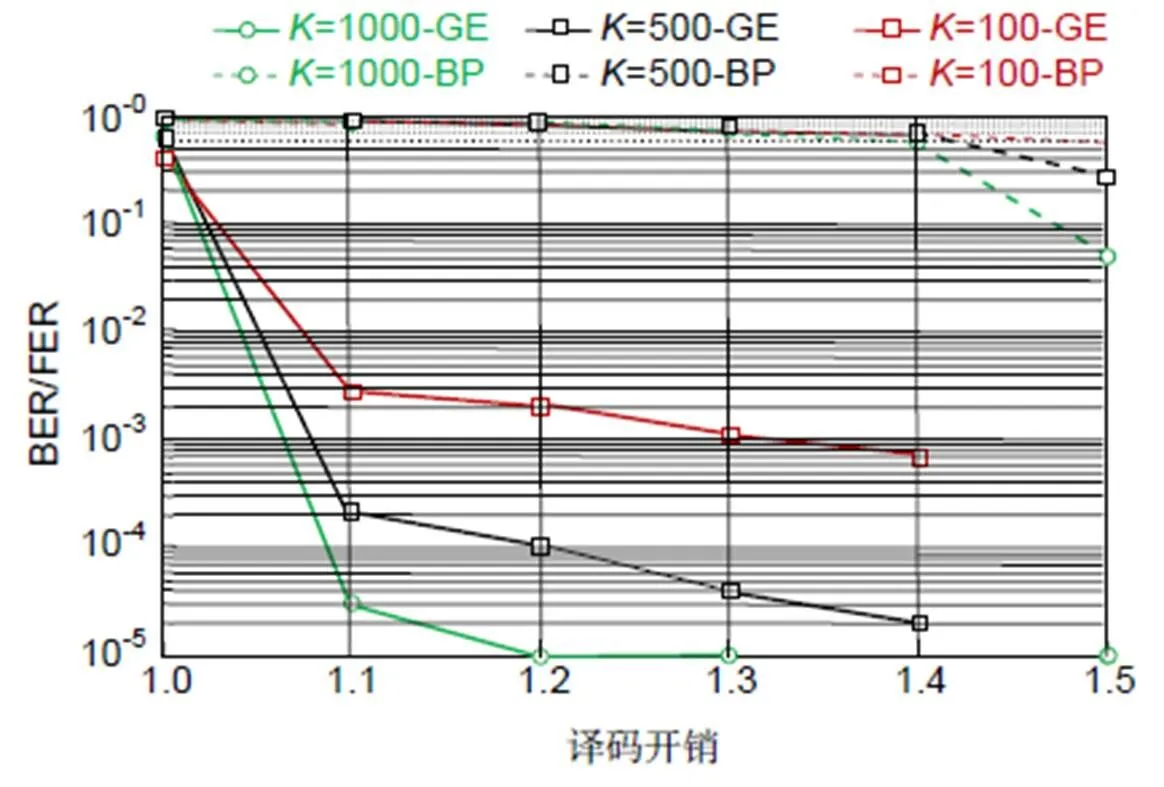
图7 LT码的BP译码和GE译码在不同码长K下的性能

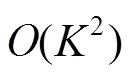
3.3.3 LT码在有噪信道下的译码

最初喷泉码的提出是基于删除信道下的，所以在有噪信道下LT码的BP译码和GE译码会更复杂。2006年Etesami和Shokrollahi等人在一般噪声二进制输入无记忆对称(binary input has no memory symmetric，BIMS)信道下利用BP译码更新的算法研究了喷泉码的性能[38]。Palanki论述了在有噪信道中考虑到译码速率和复杂性，在接收到一定数量编码符号后应当继续接收还是译码的问题[39]。Jenkac提出了在译码端设计一个度量使得有足够的编码数据被接收到时再开始译码。论证了喷泉码采用增量解码方案时，若小于最大译码迭代次数，译码器在译码尝试时进行等待操作，接收到一定编码数据才进行译码[40]。Castura等人研究了在块衰落信道中，喷泉码解码时间的分布[41]。比较流行的算法是Jenkac和Palanki等人给出了LT码在AWGN信道下的软判决译码算法先验似然对数比算法：

4 总结和展望

目前喷泉码的研究已经取得不小的成功，但目前喷泉码的研究大部分停留在理论研究和实验仿真上。喷泉码灵活多变的特性在未来的无线光通信领域有重大的应用前景，目前喷泉码亟需解决的问题有：

1) 需要借助概率论等工具从理论上分析LT码中RSD的本质原因。在源数据较大时，选用RSD的LT码有良好的性能，目前需要设计出在短码长条件下LT码性能优良的度分布。5G通信要求的高速、低时延，使得短码长在日后有重大的应用前景，所以短码长的Raptor码的性能也是亟需改善的。

2) 喷泉码本身的误码平层高于普通的线性分组码，在应用于信噪比较低的无线光通信下时会带来非常大的误差，所以优化喷泉码的误码平层构造性能更加优良的Raptor码也是未来的研究重点。

研究喷泉码与其它信道编码(如Turbo码，卷积码等)级联时的性能，以及特点级联方案优化的译码方法。将喷泉码的研究拓展到更多的信道，并对不同的信道应当由新的译码方案被提出。

3) 喷泉码在无线光通信领域的应用受到了广泛的研究。在OWC领域，将自适应技术与喷泉码相结合可以大大提高OWC系统的传输效率，充分利用频带资源；目前喷泉码应用于OWC系统的重点在于信道估计，经典的无线通信信道估计策略并不完全适合于光通信场景，所以需要设计出借助光信号对大气信道时刻变化的大气湍流、大气衰减等效应以及在深空通信中对太阳光闪烁等效应进行估计。在实际工程应用中，如何利用自适应技术来动态调整发射接收设备的相关设置，在实际信道中提升OWC系统的性能，都是发展潜力较大的领域。

[1] Xu G L, Zhang X P, Xu W H,. Free space optical communication[J]., 2002, 22(4): 198–205.

许国良, 张旭苹, 徐伟弘, 等. 自由空间光通信[J]. 光电子技术, 2002, 22(4): 198–205.

[2] Hayajneh K F, Yousefi S. Overlapped LT codes over the binary erasure channel: analysis and design[J]., 2019, 13(16): 2567–2572.

[3] Xu D Z, Xu S K, Hua J,. Recent progress on optimization design of degree distributions in digital fountain codes[J]., 2015, 30(4): 733–746.

徐大专, 许生凯, 华洁, 等. 数字喷泉码度分布优化设计的最新研究进展[J]. 数据采集与处理, 2015, 30(4): 733–746.

[4] Xiong K, Zhang Y, Fan P Y,. Evaluation framework for user experience in 5G systems: on systematic rateless-coded transmissions[J]., 2016, 4: 9108–9118.

[5] Luby M. LT codes[C]//, 2002: 271–280.

[6] Byers J W, Luby M, Mitzenmacher M. A digital fountain approach to asynchronous reliable multicast[J]., 2002, 20(8): 1528–1540.

[7] Luby M G, Mitzenmacher M, Shokrollahi M A,. Practical loss-resilient codes[C]//, 1997: 150–159.

[8] Mirrezaei S M, Faez K, Yousefi S. Towards fountain codes[J]., 2014, 77(2): 1533–1562.

[9] Byers J W, Luby M, Mitzenmacher M. A digital fountain retrospective[J]., 2019, 49(5): 82–85.

[10] Palanki R, Yedidia J S. Rateless codes on noisy channels[C]//, 2004: 37.

[11] Castura J, Mao Y. Rateless coding over fading channels[J]., 2006, 10(1): 46–48.

[12] Jiao J, Qinyu Z, Hui L. Design of Concatenated Fountain Code in Deep Space Communication[C]//, IEEE, 2009.

[13] Rahnavard N, Vellambi B N, Fekri F. Rateless codes with unequal error protection property[J]., 2007, 53(4): 1521–1532.

[14] Wu G, Yang C Y, Li S Q,. Recent advances in energy-efficient networks and their application in 5G systems[J]., 2015, 22(2): 145–151.

[15] Zhang X, Cao Y, Peng X F,. Performance analysis of LT codes in MIMO-FSO system[J]., 2017, 38(3): 61–64.

张勋, 曹阳, 彭小峰, 等. MIMO-FSO系统中LT码的性能分析[J]. 激光杂志, 2017, 38(3): 61–64.

[16] Puducheri S, Kliewer J, Fuja T E. Distributed LT codes[C]//2006: 987–991.

[17] Puducheri S, Kliewer J, Fuja T E. The design and performance of distributed LT codes[J].2007, 53(10): 3740–3754.

[18] Hyytia E, Tirronen T, Virtamo J. Optimal Degree Distribution for LT Codes with Small Message Length[C]//INFOCOM 2007. 26 IEEE International Conference on Computer Communications, 2007.

[19] Sejdinovic D, Vukobratovic D, Doufexi A,. Expanding window fountain codes for unequal error protection[J]., 2009, 57(9): 2510–2516.

[20] Bioglio V, Grangetto M, Gaeta R,. On the fly gaussian elimination for LT codes[J]., 2009, 13(12): 953–955.

[21] Sorensen J H, Koike-Akino T, Orlik P,. Ripple design of LT codes for BIAWGN channels[J]., 2014, 62(2): 434–441.

[22] Yao W Q, Yi B S, Huang T Q,. Poisson robust soliton distribution for LT codes[J]., 2016, 20(8): 1499–1502.

[23] Zhang X. Research on fountain code and its cascade over atmospheric laser communication[D]. Chongqing: Chongqing University of Technology, 2018.

张勋. 大气激光通信中喷泉码及其级联码技术研究[D]. 重庆: 重庆理工大学, 2018.

[24] Cao Y, Zhang X, Peng X F,. Cascade scheme based on multiple-input multiple-output in spatial optical communication[J]., 2018, 38(1): 0106003.

曹阳, 张勋, 彭小峰, 等. 空间光通信中基于多输入多输出的级联码方案研究[J]. 光学学报, 2018, 38(1): 0106003.

[25] Lázaro F, Liva G, Bauch G. Inactivation decoding of LT and Raptor codes: analysis and code design[J]., 2017, 65(10): 4114–4127.

[26] Byers J W, Luby M, Mitzenmacher M,. A digital fountain approach to reliable distribution of bulk data[C]//, 1998: 56–67.

[27] MacKay D J C. Fountain codes[J]., 2005, 152(6): 1062–1068.

[28] Liang M S, Duan J J, Zhao D F. Optimal redundancy control strategy for fountain code-based underwater acoustic communication[J]., 2018, 6: 69321–69334.

[29] MacKay D J C.,,[M]. Cambridge: Cambridge University Press, 2003.

[30] Li G T, Wu H K, Lee H C,. Systematic physical-layer raptor coding to attain low decoding complexity[J]., 2018, 22(6): 1124–1127.

[31] Karp R, Luby M, Shokrollahi A. Finite length analysis of LT codes[C]//, 2004: 39.

[32] Di C Y, Proietti D, Telatar I E,. Finite-length analysis of low-density parity-check codes on the binary erasure channel[J]., 2002, 48(6): 1570–1579.

[33] Xu S K, Xu D Z. Design of degree distributions for finite length LT codes[J]., 2018, 98(2): 2251–2260.

[34] Abbas R, Shirvanimoghaddam M, Huang T,. Novel design for short analog fountain codes[J]., 2019, 23(8): 1306–1309.

[35] Huang W Z. Investigation on digital fountain codes over erasure channels and additive white Gaussian noise channels[D]. Columbus: Ohio University, 2012.

[36] Khonsari H, Okpotse T, Valipour M,. Analysis of ripple size evolution in the LT process[J]., 2018, 12(14): 1686–1693.

[37] Kim S, Ko K, Chung S Y. Incremental Gaussian elimination decoding of raptor codes over BEC[J]., 2008, 12(4): 307–309.

[38] Etesami O, Shokrollahi A. Raptor codes on binary memoryless symmetric channels[J]., 2006, 52(5): 2033–2051.

[39] Palanki R. Iterative decoding for wireless networks[D]. Pasadena, California: California Institute of Technology, 2004.

[40] Castura J, Mao Y Y. When is a message decodable over fading channels?[C]//, 2006: 59–62.

[41] He J G, Hussain I, Li Y,. Distributed LT codes with improved error floor performance[J]., 2019, 7: 8102–8110.

[42] Auguste, Poulliat C, Declercq D. Jointly Decoded Raptor Codes: Analysis and Design for the BIAWGN Channel[J]., 2009, 2009:1–11.

[43] Liu X, Lim T J. Fountain codes over fading relay channels[J]., 2009, 8(6): 3278–3287.

[44] Subhagya A A M, Kaythry P, Kishore R. LT code based forward error control for wireless multimedia sensor networks[C]//, 2017: 1612–1616.

[45] Borkotoky S S, Pursley M B. Fountain-coded broadcast distribution in multiple-hop packet radio networks[J]., 2019, 27(1): 29–41.

[46] Spencer J, Hayajneh K F, Yousefi S. Robust quaternary fountain codes in AWGN interference[J]., 2018, 12(20): 2561–2567.

[47] Deng D C, Xu D Z, Xu S K. Optimisation design of systematic LT codes over AWGN multiple access channel[J].s, 2018, 12(11): 1351–1358.

Development and prospect of fountain codes in optical wireless communication

Wu Yi, Liu Hongzhan*, Hao Yuan, Liu Liyuan

Guangdong Provincial Key Laboratory of Nanophotonic Functional Materials and Devices, School of Information and Optoelectronics, South China Normal University, Guangzhou, Guangdong 510006, China

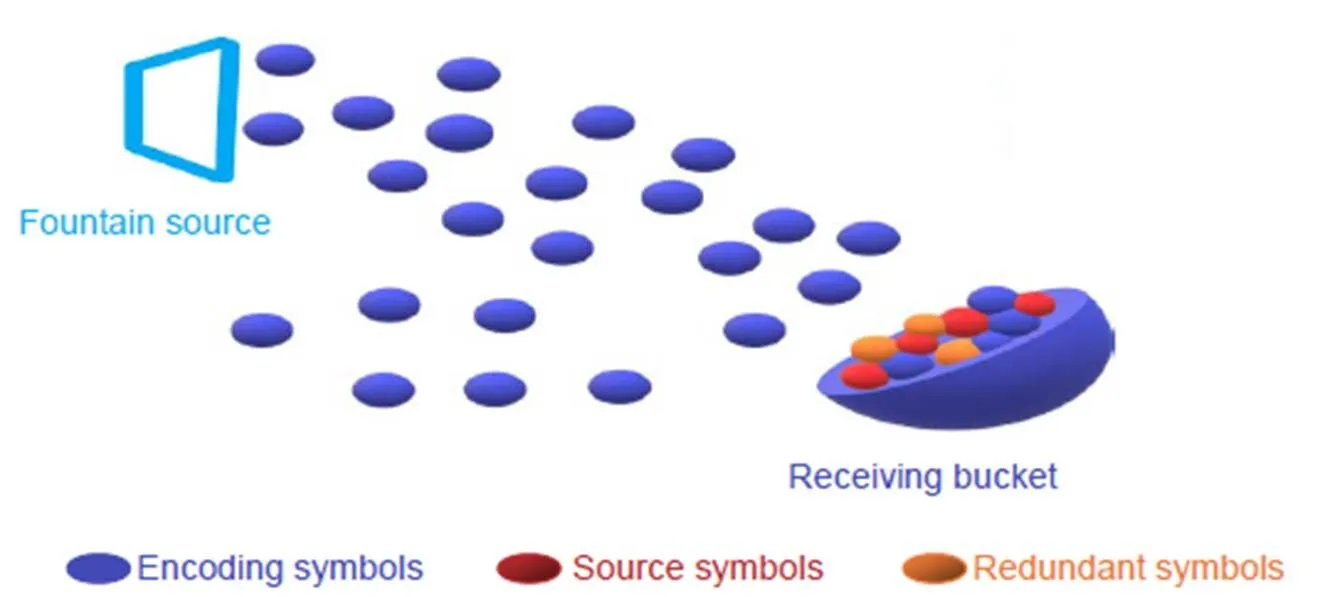
The principle of fountain codes

Overview:Fountain codes is a typical rateless coding scheme, which can also provide reliable guarantee for data transmission without channel feedback or channel estimation, and exhibit excellent adaptability to complex and variable optical wireless communication (OWC) channels. This paper reviews the development of fountain codes proposed nearly three decades ago. In 1998, Luby and other scholars proposed the concept of digital fountain in the context of solving large-scale data reliability transmission and broadcasting or multicast. Until 2002, Luby and his team designed the first practical fountain codes which be called Luby transform (LT) codes. In the theory of LT codes, robust soliton distribution (RSD) is innovatively proposed to regularize the choice of source symbols. In 2004, in order to solve the disadvantages of LT codes such as the high complexity and disability of realizing linear-time encoding or decoding, Shokrollahi et al. proposed a novel encoding scheme named Raptor (rapid tornado) codes that creatively concatenates linear block codes and LT codes together. They also optimized the fixed distribution function of Raptor codes for different information lengths. After that, some new digital fountain codes such as system fountain codes, incremental codes, spinal codes and Kite codes were successively proposed these years. Although the fountain codes was originally proposed for erasure channels, since it has great adaptivity in various channel conditions, the research of fountain code has been extended to the wireless channel in 2006, and the soft decision decoding algorithm for the fountain codes under wireless channels was obtained. At present, the fountain codes has been widely applied in wireless communication relay, space diversity, wireless cooperative transmission, etc. Thanks to its rateless characteristics, any number of coded packets can be adaptively generated according to channel conditions, producing excellent performance under erasure channel. However, when fountain codes are used in wireless channels, the design of the coding and degree distribution need to be reconsidered, which often causes the problem of high complexity and error floor. Therefore, the research hotspot of the fountain code under optical wireless communication is to cascade it with the channel coding schemes with capability of error detection, so that the fountain code can also exert its advantages under the noise channel. In short, the application prospects of fountain codes in OWC will be promising. This review focuses on the principle of fountain code and the fountain code with excellent performance, and it sheds some light on the future application of fountain code in scenario of OWC.

Citation: Wu Y, Liu H Z, Hao Y,Development and prospect of fountain codes in optical wireless communication[J]., 2020, 47(3): 190623

Development and prospect of fountain codes in optical wireless communication

Wu Yi, Liu Hongzhan*, Hao Yuan, Liu Liyuan

Guangdong Provincial Key Laboratory of Nanophotonic Functional Materials and Devices, School of Information and Optoelectronics, South China Normal University, Guangzhou, Guangdong 510006, China

The optical wireless communication channel is complex and changeable. Fountain codes as an emerging rateless coding can achieve adaptive transmission in different channel environments without a priori information of the channel. Compared with traditional coding, it can improve the quality of wireless transmission. In this paper, we first summarize the advantages of fountain codes applied to optical wireless communication and the domestic and foreign researches on the development status of fountain codes. Then we deeply study the design of two kinds of fountain codes coding schemes, as well as the degree distribution function which has significant influence on the performance of fountain code. Soon we put forward one kind of fountain codes, namely Luby transform (LT) codes, and introduce the optimization schemes in recent years. Meanwhile, the key difficulties that need to be solved in the fountain codes design are pointed out. Finally, the necessary technologies and explorations direction of fountain codes for wireless optical communication are proposed.

optical wireless communication; fountain codes; rateless coding; degree distribution functionC

TN929.1

A

10.12086/oee.2020.190623

: Wu Y, Liu H Z, Hao Y,. Development and prospect of fountain codes in optical wireless communication[J]., 2020,47(3): 190623

2019-10-16；

2019-12-25基金项目：国家自然科学基金资助项目(61875057，61475049)

吴一(1995-)，男，硕士研究生，主要从事自由空间光通信技术的研究。E-mail：1121377742@qq.com

刘宏展(1975-)，男，博士，教授，博士生导师，从事空间光通信、图像处理及光传感技术方面的教学和研究工作。 E-mail: lhzscnu@163.com

吴一，刘宏展，郝源，等. 无线光通信中喷泉码的发展现状与展望[J]. 光电工程，2020，47(3): 190623

Supported by National Natural Science Foundation of China (61875057, 61475049)

* E-mail: lhzscnu@163.com