数学归纳法的应用与建议

纪定春 蒋红珠 王若飞

(1.四川省成都师范大学数学科学学院 610068；2.广东省广州市华南师范大学数学科学学院 510631)

一、数学归纳法的发展及简介

数学归纳法是一种基本的数学证明方法，主要用于证明与正整数有关的一些数学命题，它是沟通特殊到一般、有限到无限的桥梁.数学归纳法的思想起源于毕达哥拉斯时代，从特殊的点子数出发，归纳出一般结论.欧几里得对素数有无穷的证明过程，充分地体现了数学归纳法中归纳递推的思想.13世纪末，法国数学家莱维·本·热尔松在证明排列组合问题时，用了现代意义下数学归纳法中的归纳奠基和归纳推理的思想，这标志数学归纳法逐渐走向成熟.帕斯卡在证明帕斯卡三角时，明确运用了现代意义上的数学归纳法的两个核心步骤，即归纳奠基和归纳推理两个步骤，这意味着数学归纳法证明的正式确立.意大利数学家皮亚诺发表了《算术原理新方法》，建立了自然数五条公理，数学归纳法有了理论依据，标志着数学归纳法走向成熟.随后，数学归纳法呈现多样化的发展，形成了不同类型的归纳法，如第二数学归纳法、跷跷板归纳法、倒推归纳法、跳跃归纳法、累积归纳法、无穷归纳法、区间归纳法等.接下来将介绍第一数学归纳法(以下均简称：数学归纳法)及其应用.

数学归纳法：

假设命题P(n)是关于正整数n的命题，如果P(n)满足：(1)命题P(1)为真.(2)假设命题P(k)为真，证明命题P(k+1)为真.由命题(1)、(2)为真，则对正整数n，都有命题P(n)成立.

验证命题P(1)为真，称为归纳奠基；通过假设命题题P(k)为真，证明命题P(k+1)为真，称为归纳递推(归纳推理)；最后步骤为下结论.

二、数学归纳法的应用

1.求证数列通项中的应用

例1(2014年广东高考数学卷)设数列{an}的前面的n项和为Sn，关系为Sn=2nan+1-3n2-4n，n∈N*，且S3=15.(1)求a1，a2，a3的值；(2)求数列{an}的通项公式.

解析对问题(1)，由于数列Sn，满足Sn=2nan+1-3n2-4n.容易得a1=3，a2=5，a3=7.

对问题(2)，由问题(1)中a1，a2，a3值，猜数列{an}通项为：an=2n+1.

现在用数学归纳法来证明以上的猜想.

(1)当n=1时，显然结论成立.

(2)假设当n=k时结论成立，即ak=2k+1，前k项和为Sk=3+5+…+(2k+1)=k(k+2).

由数列Sk满足Sk=2kak+1-3k2-4k.

则k(k+2)=2kak+1-3k2-4k，整理可得ak+1=2k+3.

即ak+1=2(k+1)+1，所以当n=k+1时成立.

由(1)和(2)，对任意的n∈N*，有an=2n+1.

故数列{an}通项为an=2n+1.

评注该试题的第二个问题，巧用问题(1)的结果，先猜测出数列的通项相公式，然后再证明猜想，充分体现了“先猜后证”的思维模式，在数学史上很多数学结论的发现，往往就是建立在已有的知识基础上，利用先猜想后证明的方式进行的.

2.证明不等式中的应用

例2(2019年浙江高考数学卷第20题)设等差数列{an}的前n项和为Sn，a3=4，a4=S3，数列{bn}满足：对每个n∈N*，Sn+bn，Sn+1+bn，Sn+2+bn成等比数列.

(1)求数列{an}，{bn}的通项公式；

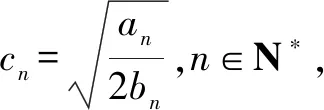
解析问题(1)，解答过程略.利用等差数列和等比数列的知识点及上述的关系式可得，数列an=2n-2，bn=n2+n，其中n∈N*.

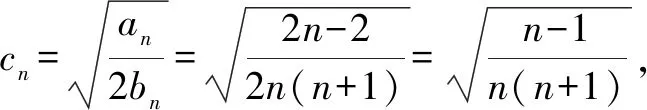
显然这个不等式是关于正整数n的命题，考虑用数学归纳法证明.

(1)当n=1时，有c1=0<2，显然不等式成立.

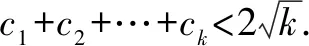
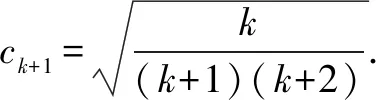
即当n=k+1时，不等式成立.

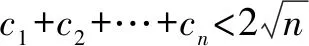
评注该试题从直接法不容易解决，又注意到需要求证的命题为一个关于正整数n的命题，自然想到使用数学归纳法.

例3(2014安徽高考数学理科卷第21题)设c>0，整数p>1，p∈N*.(1)证明：当x>-1且x≠0时，有(1+x)p>1+px；(2)略.

BP神经网络是目前应用最广泛的神经网络，是一种复杂的非线性映射系统，能以任意精度逼近，削弱坐标转换中的系统误差与异常误差等因素的影响。但该方法具有容易陷入局部极小值、外推能力差等缺点，因此，还需要研究改进神经网络学习算法，进一步提高该方法在坐标转换中的精度与可靠性。

证明问题(1)是关于正整数p的命题，考虑使用数学归纳法.①当p=2时，有(1+x)2=1+2x+x2.当x>-1且x≠0，有x2>0，故(1+x)2>1+2x成立.②假设当p=k(k≥2)时，命题(1+x)k>1+kx成立.由假设可得(1+x)k+1=(1+x)k(1+x)>(1+kx)(1+x)=1+(k+1)x+kx2.因为kx2>0，所以(1+x)k+1>1+(k+1)x.故当p=k+1时命题成立.

由①和②知，对于任意的整数p>1，p∈N*，当x>-1且x≠0时，有不等式(1+x)p>1+px成立.

评注该试题的解法除了数学归纳法之外还有其它方法，如二项式展开、伯努利不等式.解决该问题的关键在于巧用“(1+x)k+1”的变形，然后根据假设的不等式进行放缩.

3.证明整除性中的应用

例4证明：当n∈N*时，11n+2+122n+1能够被133整除.

证明这是一个关于正整数n的整除性命题问题，考虑使用数学归纳法.

(1)当n=1时，11n+2+122n+1=113+123=(11+12)(112-11·12+122)=23×133.则当n=1时，能被133整除.

(2)假设当n=k时，11k+2+122k+1能够被133整除.

当n=k+1时，有11n+2+122n+1=11k+3+122k+3，采用“配凑法”变形可得11k+3+122k+3=133×122k+1+11×(11k+2+122k+1).

其中133×122k+1能够被133整除.

由假设可知11k+2+122k+1能够被133整除，故11×(11k+2+122k+1)被133整除.

因此当n=k+1时，11n+2+122n+1=11k+3+122k+3能被133整除.

由(1)和(2)可知，对任意的n∈N*，11n+2+122n+1能被133整除.

评注解决该整除性命题的关键在于巧妙运用“配凑法”，将“11k+3+122k+3”与“11k+2+122k+1”建立联系，再由假设可以证当n=k+1时命题成立.

4.证明恒等式中的应用

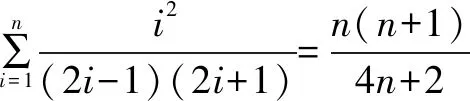
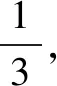
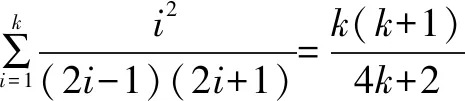
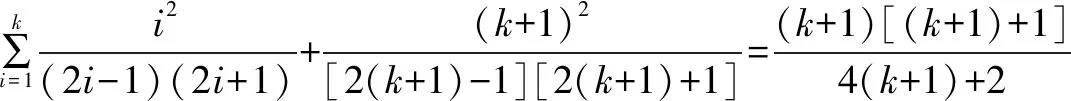
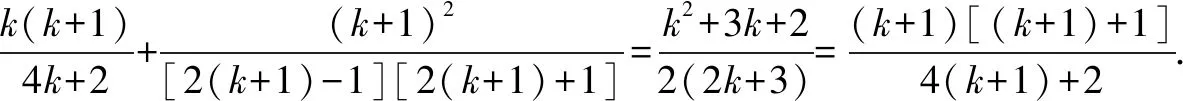
故当n=k+1时，等式成立.

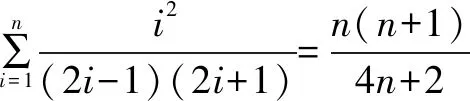
评注该试题的思路可以归结为：观察→试算→猜想→验证(证明).这一步的推理过程是需要进行严密的逻辑推理的.经过了观察、试算、猜想，并不能够说明猜想的结果是正确的，这时需要用数学归纳法进行验证.

三、建议

在最近的几次课程改革中，数学归纳法一直不被重视，以前高考要考，老师要教，现在的高考数学对数学归纳法已经不作要求，很多高中老师已不讲，甚至不提数学归纳法，显然是对数学归纳法的重要性认识还不够，也是对人类智慧结晶的损失.数学归纳法是一种重要的数学证明方法，建议将数学归纳法的内容纳入高中数学必修内容.原因如下，其一，数学家庞加莱和华罗庚先生都十分地推崇数学归纳法；其二，数学归纳法作为人类智慧的结晶，是在历经了千年的发展中逐渐成熟和丰富的，是人类从有限证明向无限证明的飞跃，是人类认识无限的光辉范例；其三，数学归纳法是发展的，具有强劲的生长力，通过数学归纳法可以派生出很多其它类型的归纳法，因此可以认为数学归纳法是其它归纳法的“母本”；其四，高等数学中常常用数学归纳法来证明关于自然数的无限命题，以《高等代数(第四版)》(北大数学系前代数小组编)为例，使用数学归纳法证明定理、例题(不含课后习题)高达18次，足见数学归纳法在高等数学中的重要地位；其五，发达国家对数学归纳法的要求较高，且普遍高于我国的要求，如日本、美国等.其六，数学归纳法蕴含丰富的文化内涵，是文化育人的好素材.最后，数学归纳法在高中阶段是可教的、可学的，有很多优秀的教学案例可以帮助教师的教和学生的学习.因此，建议在下一次修订高中数学课程标准时，将数学归纳法纳入必修内容.