二次型递推关系数列的处理策略

李秀元 朱丹丹

(湖北省武穴市实验高级中学 435400)

数列的递推关系有很多种，通过递推关系可以研究数列的特点，求数列的通项公式.一般地，二次型递推关系可分为二次函数型、均值型和圆型三大类.

一、二次函数型递推关系

所谓二次函数型递推关系，就是将数列的项表示成前一项的二次函数.这类递推关系式，大致有下面三种考查角度.

1.考查数列的周期性

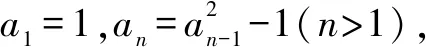
解由递推关系可得，a1=1，a2=0，a3=-1，a4=0，a5=-1，则数列{an}除第一项外，构成周期为2的周期数列.故a2019=a3=-1，|an+an+1|=1.

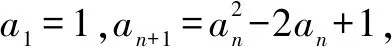
解由递推关系可得，a1=1，a2=0，a3=1，a4=0，则数列{an}是周期为2的周期数列，故a2020=a2=0.

方法归纳如果不是求特殊数列(如等差等比等)的较大项，一般是考查数列的周期性，通过递推关系式，尝试求出数列的前几项，以发现规律性.

2.考查逻辑判断与数据处理

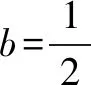
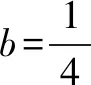
C.当b=-2时，a10>10

D.当b=-4时，a10>10

分析作为选择压轴题，这道题确实有些份量.由于递推关系式没有现成的处理模式，不知道考什么，很难切入.从4个选项来看，都是基于b的取值，确定a10>10.结论都是与a无关，即认为是对实数a恒成立的问题，而且，对数列的特性也未作说明.若从数列{an}的特性来看，常数列是特殊的等差和等比(项非零)数列.因此，可以考虑以常数列为基准，通过赋值a，构建反例，进行计算排除.

解若数列{an}为常数列，设an+1=an=λ.

对于选项C，方程λ2-λ-2=0的根为λ=2或λ=-1，无论取an=a=2还是-1，都不满足结论；

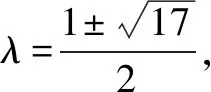
因此，只能选A.

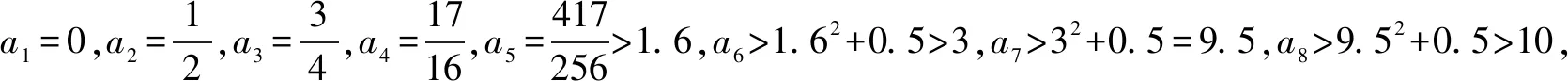
3.考查二次式的配方与对数运算

例4(2006年山东卷)已知a1=2，点(an，an+1)在函数f(x)=x2+2x的图象上，其中n=1，2，3，….

(1)证明数列{lg(1+an)}是等比数列；

(2)设Tn=(1+a1)(1+a2)…(1+an)，求Tn及数列{an}的通项；

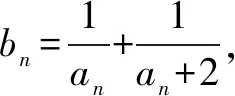
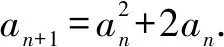
(1)因为a1=2，所以an>1.

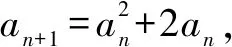
(2)由(1)得lg(1+an)=2n-1lg3=lg32n-1，所以1+an=32n-1，an=32n-1-1.

Tn=(1+a1)(1+a2)…(1+an)=320+21+…+2n-1=32n-1.

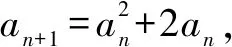
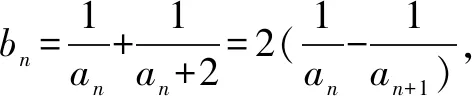
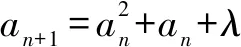
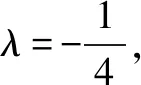
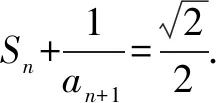
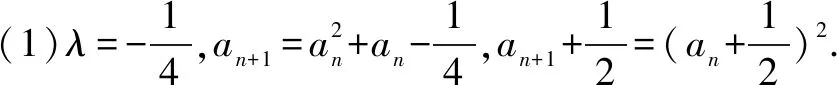
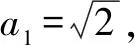
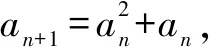
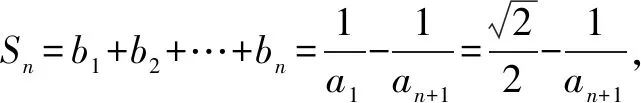
方法归纳对原递推关系式中的二次项配方，得到相同结构的两项的二次关系，明确项的符号后，对两边取对数，得到一个新数列的线性递推关系，进而求出数列的通项.

二、均值型递推关系

所谓均值型递推关系，即将数列的项用它的前一项的均值型表示.相对于简单的二次函数型递推关系式，这类递推式处理起来就要麻烦得多，需要进行两次配方.

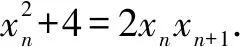
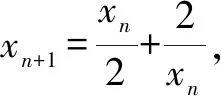
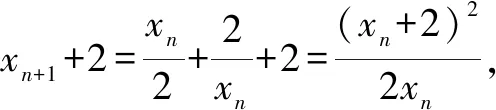
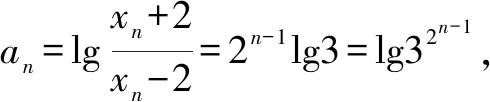
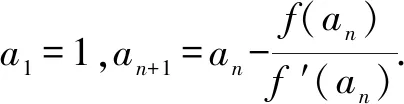
(1)求α，β的值；

(2)证明：对任意的正整数n，都有an>α；

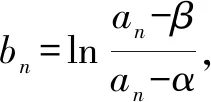
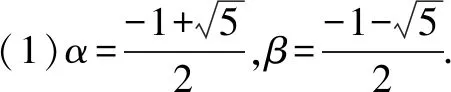
(2)因为f′(x)=2x+1，

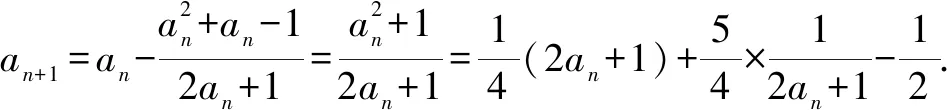
由a1=1，得an>0.

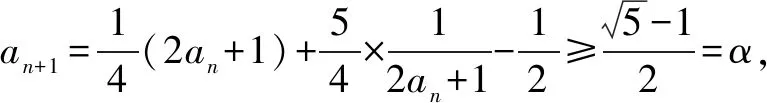
(3)f(an)=(an-α)(an-β)，f′(an)=2an+1.

又α+β=-1，

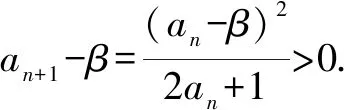
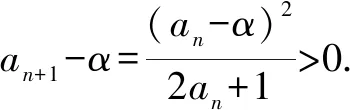
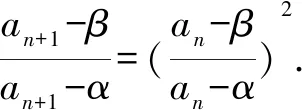
方法总结通过两次对递推关系式左右两边加减相同常数，使得等式右边分子为完全平方，两式相除，即得类型三.

三、圆型递推关系

圆型递推关系，即是数列相邻两项满足圆的方程，也即点(an，an+1)在圆上.

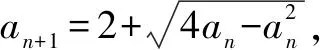
解法1由已知得0≤an≤4，且an+1≥2.

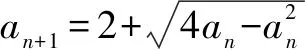
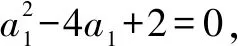
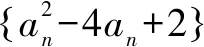
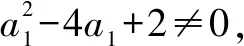
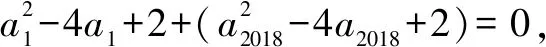
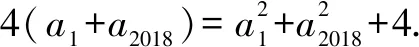
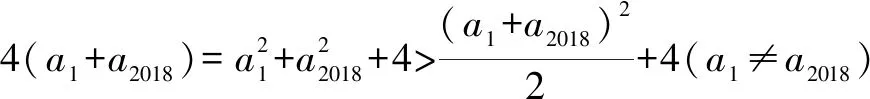
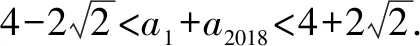
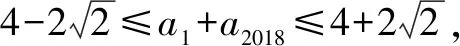
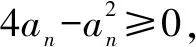
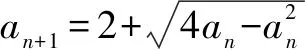
令an-2=2cosθ(θ∈[0,π])，an+1-2=2sinθ.

即an=2+2cosθ，an+1=2+2sinθ.

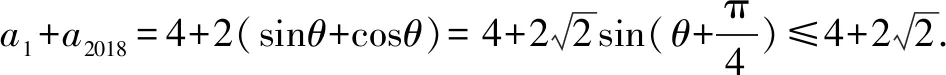
(由于a1和a2018分别对应数列的奇偶项，故它们使用了不同的表达式)