液滴撞击固体壁面研究进展

梁 超， 廖 熠， 张芳芳， 宋静艳， 黄 华

(1.四川轻化工大学土木工程学院， 四川 自贡 643000；2.郑州轻工业大学能源与动力工程学院， 郑州 400044)

引 言

液滴撞击固体壁面、液池、液膜这一现象广泛存在于自然、生活、工农业生产的各领域。结冰气象条件下，导致飞机发生飞行事故的主要原因之一则是大气中的过冷液态水撞击机翼表面产生结冰行为[1]。喷雾冷却过程中液滴撞击热壁面、薄液膜发生热质交换过程对发热元件或者热壁面的冷却效果起主要决定作用[2-3]。微液滴喷射过程中液滴喷射状态、表面张力、液体粘度、液滴铺展行为对喷墨印品质量至关重要[4]。内燃机中燃料的喷射碰撞对发动机效能起到非常重要的作用[5-6]。

液滴撞击是一个复杂的流体动力学过程，涉及气液两相流动，相变传热传质以及液固耦合作用。液滴撞击固体壁面后会发生铺展、破碎、飞溅和反弹等形态变化[7-8]，其变化过程与液滴自身特性，如液体粘性、表面张力、液滴大小、撞击速度、液滴温度等密切相关，同时也和撞击壁面形态、温度、粗糙度、浸润性、壁面结构等有关[9-10]。

自1908年Worthington[11]首次研究液滴撞击壁面和液池所产生的特殊现象以来，一百多年来国内外的研究者对液滴碰撞壁面形态变化规律以及热质交换过程进行了大量的研究，已有文献报道主要集中在理论分析、数值模拟和实验研究三个方面。但还少有文章对该领域的研究进行梳理和总结，因此本文将对液滴撞击固体壁面动态特性以及其影响因素进行综述，深入了解液滴撞击过程的动力学行为，以期为相关技术领域的问题提供帮助。

1 液滴撞击壁面理论研究现状

1.1 液滴撞击壁面动态行为

液滴撞击固体壁面后，根据液滴物性以及壁面状态的不同会产生铺展、回缩、沉积、飞溅，反弹等几种动态行为[12-14]，如图1所示。当液滴具有较高润湿性且撞击速度较小时，撞击壁面后完全铺展且液膜几乎不收缩，即完全铺展后沉积状态；撞击速度较大，或壁面形态不规则粗糙度较大时，液滴撞击壁面后会产生快速溅射现象，即相较于铺展过程的完整液膜而言，液膜呈破碎甚至飞溅状态；其中有种形似皇冠状的溅射称为“冠状溅射”，其产生原因学者多倾向于归结为Rayleigh-Taylor不稳定性[16]，受周围气体的阻力作用，液滴在径向铺展过程中液膜边缘的部分液体向上运动呈皇冠形。在超疏水表面以及壁面温度较高的情况下，液滴撞击壁面后则会出现部分或者完全反弹脱离壁面的现象[14]。覃群[17]建立TAR模型，将液滴撞击后动态过程比作一个有阻尼弹簧运动系统，得到液滴撞击后发生反弹的临界韦伯数和临界反弹速度，且与实验值吻合。

(a)铺展沉积，(b)快速飞溅，(c)冠状溅射，(d)后退破裂，(e)部分反弹，(f)完全反弹[14]

1.2 最大铺展直径

液滴撞击壁面后所能达到的最大铺展直径直接影响到喷墨质量和液体与壁面之间热质交换效果，由于液滴撞击过程的复杂性，对最大铺展直径的理论推导主要从两个方面考虑：

一种是分别建立液滴初始和铺展达到最大直径状态时的能量方程，从能量守恒的角度推导液滴撞击后所能达到的最大铺展直径。这其中，关于运动过程中的粘性耗散能的准确界定存在较大困难，导致不同的最大铺展直径模型之间存在一定差异。Collings[15]假设铺展最终状态为圆盘形，忽略粘性耗散，基于能量守恒推导出最大直径铺展系数为：

βmax=((We+12)/3(1-cosθ))1/2

(1)

为了考虑粘性耗散的影响，Avedisian[19]对粘性耗散能采用下列公式求解：

(2)

求得最大铺展系数为：

βmax≈[1/3(We+4)/(1-cosθ)]1/2

(3)

Pasandideh-Fard[16]对以往的铺展系数求解公式进行了改进，认为粘性耗散绝大部分产生在边界层，并对计算过程中的体积表达式进行改进，得到铺展系数公式为：

(4)

Ukiwe[18]在实验过程中发现已有文献中最大铺展直径模型与实验结果存在较明显的误差，选用公式(5)计算粘性耗散，最终得到最大铺展直径与实验结果偏差小于5%。

(5)

李西营[30]则对超疏水表面上液滴撞击最大铺展直径进行理论预测，模型中既考虑了液滴在微结构表面内流动所产生的粘性耗散，同时也考虑了超疏水表面上液滴运动过程表面能变化，因此相较于前人的模型有更高的准确性。其计算公式如下：

(6)

除了能量守恒的角度，另外一种则是从流体动力学角度出发分析撞击过程。通过建立质量守恒方程，N-S方程，考虑动态过程中接触角、毛细力等影响因素，对最大铺展直径进行理论求解。由于理论求解的困难，往往要进行诸多的假设和简化，尽管如此，理论推导结果对液滴撞击过程动态行为变化能够给出较合理的解释。不论是哪种方式，由于液滴动态过程本身的复杂性，较为准确的理论求解始终存在较大的困难。

2 液滴撞击壁面实验研究

囿于理论研究的困难性，大量学者对液滴撞击壁面的动态特性进行了实验研究。针对不同的研究领域对液滴撞击不同固体壁面后动态特性进行了实验研究，包括亲水、疏水、超疏水、加工过的微结构表面以及多孔介质表面等[22-24]。或者对液滴与壁面所处的相对位置不同，不同的壁面形态等进行实验研究[25-26]，如垂直撞击，倾斜撞击，球形曲面，圆柱形曲面等。

2.1 壁面润湿性

液滴撞击不同润湿性壁面后会产生不同的动态行为，壁面润湿性由壁面本身分子结构及粗糙度所决定，采用壁面接触角(CA)反映壁面润湿性。通过制备润湿性梯度表面，发现在润湿性梯度表面上液滴会呈现自发的向润湿性较强一侧移动[27-28]。Daniel S[29]研究了不同表面张力和粘度的液滴在润湿梯度表面上运动。 当壁面接触角滞后性忽略不计时，任何大小的液滴都会自发地在这样的表面上移动，若需要考虑壁面接触角滞后性，则存在一临界尺寸，液滴大于临界尺寸时可出现自发迁移。李西营[30]通过控制有机液体扩散方法制备了轴对称、径向分布的梯度润湿表面，发现不同润湿性梯度表面液滴最终状态会不同。表面的润湿性分布会导致液滴三相接触线在不同方向上的收缩速度不同。轴对称润湿性梯度对最大铺展直径和铺展过程几乎不起作用，但表面的梯度润湿性对收缩过程有影响。液滴在亲水表面收缩时需要克服更大的表面能，因此收缩速度慢，最大铺展直径大，而疏水表面上的收缩速度快，最终铺展接触面积更小。壁面润湿性是影响液滴动态行为的关键因素之一，对相变过程中接触热阻、接触角滞后和温度对壁面润湿性影响等现象还有待进一步更为深入的研究。

2.2 不同形态壁面影响

采用微光刻等技术可以制备具有微纳米复合结构的疏水和超疏水表面[31-33]，液滴撞击微结构超疏水表面后所呈现的两种状态分别是Wenzel完全润湿状态[34]和Cassie-Baxter复合润湿状态[35]，关于两种润湿区间转换机制尚无完全充分的解释，因此研究撞击超疏水表面、润湿区间转换以及制备具有稳定超疏水特性的表面成了众多学者关注的重点。周培阳[32]等通过激光制备超疏水表面，对液滴冲击后固液接触时间进行研究，发现在相同参数下，窄脉宽条件下制备的超疏水表面微米结构更高，液滴冲击时固液粘附力增加，固液接触时间更长。Reyssat[36]通过建立能量守恒方程，推导了液滴撞击超疏水表面后发生反弹的临界速度以及液滴浸入多孔介质后微观结构内发生浸润现象的临界速度。Karapetsas[37]发现液滴撞击微结构疏水表面后卷吸空气，液滴内包裹的气泡使液滴与壁面接触角滞后减小，迁移速度增大。Quan和Zhang[38]研究液滴撞击不同微晶超疏水表面，发现壁面上的交叉柱微结构有利于液滴反弹，具有较大接触角的表面可缩短液滴与壁面的接触时间，降低液体的穿透深度。Hu H B[22]研究了液滴撞击自制的超疏水黄铜表面上的回弹行为，并从能量守恒角度，对不同的行为和回弹机理进行理论分析，实验观察到的回弹和飞溅效果与理论预测误差值约为14%。

近年来，也有相关文献研究液滴撞击倾斜壁面后的动态特性，由于重力场的作用使得撞击倾斜壁面后会出现较水平壁面上不同的动态特性，通常会有以下六种情况：沉积、溪流、滑行、旋滚、部分反弹和完全反弹[39]，并且在超疏水表面上，壁面的倾斜会增强液滴反弹和脱落。液滴撞击倾斜壁面后反弹现象产生主要取决于液滴与斜面之间的气膜厚度是否大于临界值，中间气膜对液滴下滑铺展过程起阻碍作用[49]。沿下滑面的惯性力大小变化会改变液滴在壁面的铺展程度，其形态变化以及内部压力场、温度场和速度场均呈现非对称状态，壁面换热也会呈现非对称性[50]。

关于液滴撞击圆柱壁面，曲面最早由Hung[51]研究，并对液滴从圆柱曲面脱离形式、We数以及液滴与曲面相对大小之间的关系进行揭示。陆续有更多的研究对液滴撞击圆柱曲面后液滴捕获能力、撞击速度、铺展特性，正面撞击、侧面撞击以及接触时间等进行研究[31-34]。结果表明，受壁面形状的影响，圆柱壁面上液滴沿轴向和径向的运动有明显不同，撞击后的铺展阶段，动能对铺展状态和捕获能力起主要决定作用，而在回缩阶段，除了考虑液滴本身动能，液滴与圆柱面相对大小对回缩过程中液滴形态影响较大[31]。此外液滴尺寸，与曲面相对大小比例、撞击速度均存在一临界值，超过临界值，壁面便不再具备捕获能力，液滴将完全脱离圆柱曲面[33]。

相较于平壁面研究，液滴撞击倾斜壁面、圆柱和球形等曲面后的动态特性相对研究较少，针对曲面形态，撞击速度以及壁面润湿性等对液滴撞击后的运动特性、接触时间、液体捕捉等还需要进一步研究。

3 液滴撞击壁面数值模拟研究

数值模拟是近年来新兴的一种研究方式，液滴撞击壁面过程为气液两相流动问题，准确的计算运动过程中的气液相界面是问题的关键。已有的模拟方法中，实现相界面的提取主要分为两大类，一种是基于欧拉法的界面捕捉，另一种则是基于拉格朗日法的界面追踪[44-45]。其中典型的方法有ALE(arbitray lagrange-eulerian)和欧拉-拉格朗日混合方法，MAC法。目前采用较多的是欧拉法的典型代表方法：流体体积法(VOF)[46-47]，水平集法(level-set)[44]，以及结合流体体积法和水平集法优点的LS-VOF方法[55]，此外还有基于介观尺度的格子L-B方法[10,48]。

数值模型对液滴尺寸、撞击速度、液体本身物性(表面张力、粘性)、壁面接触角、壁面润湿性，撞击入射角等因素对撞击后液滴铺展，最大铺展直径，回缩形态，破碎和反弹等动态行为进行了模拟，且液滴撞击壁面动态过程模拟结果与实验能够较好吻合，如图2所示。梁超[46,56]等对液滴撞击不同浸润性的壁面上进行模拟，发现了液滴撞击后的铺展、液膜断裂，部分和完全反弹现象。模拟结果表明随着液滴撞击速度增大，最大铺展直径增大，随着液体粘性增加，液滴铺展和回缩过程中耗能增大，对液滴动态行为起明显的抑制作用[47]，粘性和表面张力对液滴撞击后的飞溅行为影响较大，液体表面张力和粘性越小时，撞击后越容易发生飞溅。Long li[48]等采用格子LB模型模拟双液滴撞击液膜动态行为，发现粘度越小时液滴内部作用越小，液滴撞击粗糙壁面后则更容易发生飞溅行为，疏水和超疏水壁面上容易出现反弹现象。模型在对壁面润湿性的处理通常会选取某个静态接触角作为边界条件，这与实际的液滴撞击过程中变化的动态接触角存在较大的偏差，导致模拟结果和实验结果存在误差。Bussman[49]从实验照片中提取前进接触角和后退接触角，并融合到模型中对倾斜壁面和45°台阶壁面上液滴碰撞后的动态行为进行模拟，减小了模型与实验数据之间的误差。液滴铺展过程中因为与壁面之间存在温差进而产生热量交换也是导致壁面润湿性发生变化的另一个原因，叶学民[50]等则从温度对壁面润湿性和铺展过程中的影响进行探究，认为平衡接触角起关键作用。Wang和Chen[27]采用耗散离子动力学方法模拟不同润湿性支柱表面结构对液滴运动的影响，发现非均匀润湿性对液滴动态接触角有显著影响，液滴在非均匀区域滑动时，其前进角和后退角都增大。陈圆圆[51]通过在壁面上有规律的布置亲水点，采用VOF方法对“液滴微阵列”进行模拟，对非均匀润湿性壁面上液滴撞击后相较于均匀润湿性壁面的特殊动态行为进行模拟，对细胞筛选或者平板印刷等行为有特殊的指导意义。模型能够较好的计算液滴内部的压力场和速度场，从而有助于解释撞击后的动态行为。Li发现撞击后最大压应力出现在铺展过程中液滴中心的两侧[52]，这与梁超[56]等模拟发现的压力最大值出现在近壁面处液滴中心结果存在一定出入。李家宇[53]则认为相场方法在相界面的描述过程中，因为考虑了界面应力效应，对计算表面张力更有优势，采用相场方法解决接触线附近的奇异性，并结合Yokoi[54]动态接触角模型研究液滴动态润湿过程。郑志伟[55]采用复合LS-VOF方法对液滴撞击凹曲面后液滴内部流动传热以及破碎机理研究，发现撞击凹曲面上，铺展系数更小，出现回弹射流时间超前，回弹射流速度更大。梁超[56]，N. Nikolopoulos[57]等分别对液滴冲击静止，移动液膜后液冠生长和飞溅特性进行的研究，对二次液滴的直径、数量与We数之间关系进行了研究。

虽然大部分模型都能较好的模拟液滴撞击壁面和薄液膜之后所产生的铺展，回缩，反弹以及溅射等动态行为，但是对于溅射、反弹行为产生机理仍有待研究。模型中对动态接触线的边界条件仍然没有达成一致意见，润湿性和粗糙度对液滴动态演变的影响，仍需更充分的研究。 回缩后顶部形成二次小液滴，扩展和退化阶段液膜边缘的自由指状边缘等特殊现象，都需要进一步的实验和理论研究来解释。

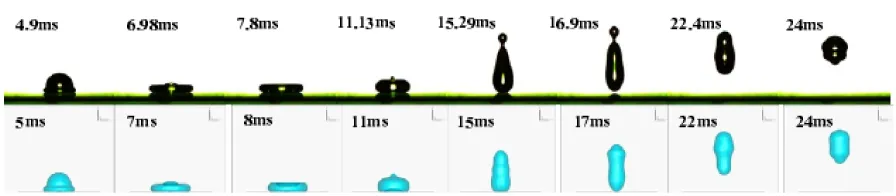
图2 液滴撞击固体表面模型与实验对比[57]

4 结论和展望

(1) 理论、实验和数值模拟三种方法均对液滴撞击壁面和液膜过程动态行为进行了揭示，并对其动态过程演变机理进行了研究。主要集中在对液滴撞击后所产生的铺展、沉积、飞溅和反弹等行为和临界条件进行揭示，铺展后所能达到的最大直径和影响因素等。对壁面粗糙度、润湿性、接触角、液体表面张力、粘性等都有较为丰富的研究。

(2) 三种方法各有优缺点，基于理论求解的方法研究最早，但由于该过程的复杂性，理论模型中的粘性耗散、接触角等诸多问题尚无较为统一的结论。目前基于实验和数值模拟的研究较多，实验方法能够对液滴和表面特性进行较为直观和客观的研究，但实验过程存在不确定影响因素，且实验成本高昂。数值模拟方法众多，成本低廉，且可对流场内部压力速度分布情况等进行分析，但其中接触线附近气液固耦合的复杂边界条件处理较困难，使得反弹、飞溅等特殊行为的模拟结果与实验结果仍有误差存在，且温度对液滴表面张力，液滴粘性，表面润湿性等的影响少有被考虑到模型中。

(3) 数值模拟方法中，单液滴撞击壁面和液膜模型研究较多，而针对特定研究领域，诸如喷雾冷却，喷雾燃烧等的多液滴撞击壁面相互作用的复杂模型则应该得到更多关注。

(4) 液滴撞击后动态演变过程中产生的某些局部特殊现象，如皇冠溅射，顶部二次小液滴，回缩断裂，自由指状边缘等还有待进一步实验和理论研究解释。