高速铁路预应力混凝土简支箱梁剪力滞效应分析

王小鹏， 张元海

（1.陕西铁路工程职业技术学院，陕西渭南 714000； 2.兰州交通大学土木工程学院，兰州 730070）

预应力混凝土简支箱梁在高速铁路桥梁建设中被广泛应用，具有受力明确，施工方便等特点. 为了准确检测和控制主梁应力，即使在大跨度预应力混凝土桥梁施工中也必须要考虑剪力滞效应的影响［1-3］，箱梁的剪力滞效应本质上是由于翼缘板的面内剪切变形引起的应力非均匀分布现象［4-6］，纵向预应力钢筋的合理布置可以减弱由于剪力滞效应引起的应力不均匀分布［7］. 牛斌等提出了考虑剪力滞效应后，预应力简支箱梁有效宽度的折减系数和竖向刚度的换算系数［8］. 张元海等分析了剪力滞效应对简支梁和连续梁跨中附加弯矩和挠度的影响［9-10］. 张慧等研究了考虑剪切变形对简支箱梁剪力滞效应的影响［11-12］. 张玉元等计算了简支梁考虑剪切效应和剪力滞效应后梁体的总挠度［13-14］. 周世军等分析了界面滑移量对组合箱梁剪力滞效应的影响［15］. 周朋等运用有限梁段法分析了连续梁悬臂施工中的剪力滞效应［16-17］. 王小鹏等分析了在斜交支承条件下箱梁剪力滞效应和约束扭转［18］.

本文以剪力滞效应引起的附加挠度作为广义位移，将预应力钢筋作为施加在混凝土结构上的外荷载进行等效计算，基于能量变分法，推导预应力作用下的剪力滞效应解析解. 同时对一简支梁建立有限元模型，通过计算对比验证本文计算精度. 以高速铁路标准跨度预应力简支箱梁为例，分析在不同布束方式下跨中截面剪力滞效应及分布规律.

1 箱梁剪力滞效应

1.1 基本变分方程推导

如图1所示，在分布荷载p(z)作用下，梁体会发生弯曲变形，结合既有文献［19］，在横截面上每一点的纵向位移u(x,y,z)可表示为：

式中：w( z )为初等梁的挠度；f( z )为剪力滞效应引起的附加挠度；wζ(x,y)为剪力滞翘曲位移函数；η 为剪力滞翘曲应力自平衡修正系数；ω( x,y )为附加挠曲转角-f′(z)对应的剪力滞广义翘曲位移函数，即

则横截面上任一点的正应力σ(x,y,z)与切应力τ(x,y,z)为：

式中：G为剪切弹性模量；E为杨氏弹性模量.

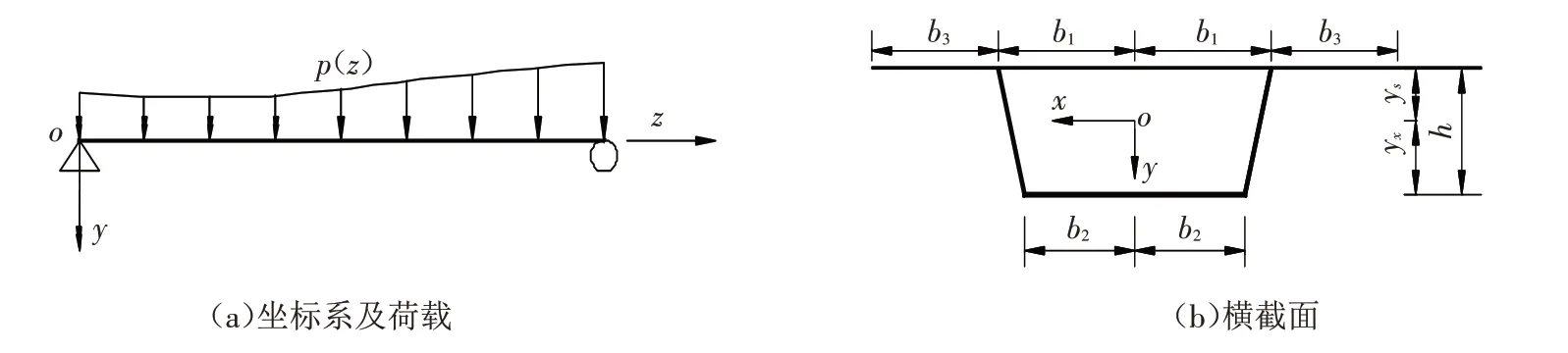
图1 箱梁横截面尺寸Fig.1 Box girder dimension

由式（3）可知，剪力滞翘曲应力为σω，

根据剪力滞翘曲正应力在横截面上应力自平衡可得，

式中：Ix为截面对水平形心轴的惯性矩，Ix=∫Ay2dA；Iyζ为剪力滞翘曲惯性积，Iyζ=∫AyωζdA，A为箱梁横截面面积.

定义与剪力滞翘曲应力σω对应的内力为剪力滞广义力矩Mω.

将式（4）代入式（6）得：

式中：Iω是剪力滞广义翘曲惯性矩；Iω=∫Aω2dA.

在考虑箱梁剪力滞效应后，横截面上的总应力为：式中：M为初等梁理论弯矩.

在竖向外荷载p( z )作用下，梁体的总势能Π 为：

式中：Aζ=∫(∂ωζ/∂x)2dA .

本文选取的剪力滞翘曲位移函数选为：

其中：d为考虑剪力滞翘曲应力自平衡的另一个修正系数，

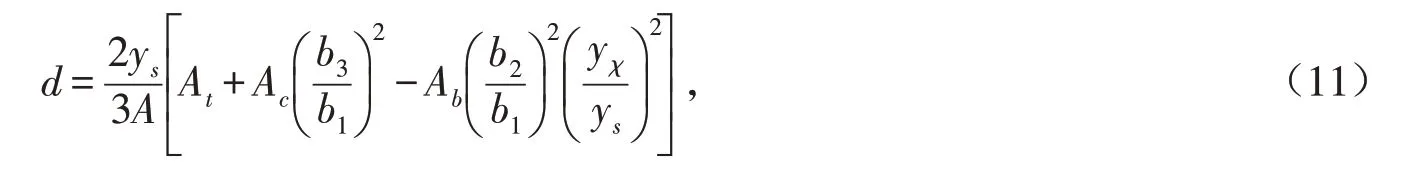
式中：At、Ab和Ac为箱梁顶、底板和两侧悬臂板的截面积；A为箱梁横截面面积；ys和yχ为箱梁形心轴分别到箱梁顶板和底板的距离；b1、b2和b3为箱梁横截面尺寸，如图1（b）所示.

将式（3）代入式（9）并进行一阶变分计算，根据最小势能原理可得微分控制方程：

将式（12）简化处理，可得到关于剪力滞附加挠度的控制微分方程：

1.2 边界条件

对于微分方程（13），是以剪力滞附加挠度为基本未知量，边界条件可根据梁端的约束条件而得：固定端：f=0，f′=0；简支端：f=0，f″=0；自由端：f″=0，f‴-k2f′=0 .

2 预应力作用下的剪力滞效应

2.1 预应力钢筋的等效荷载

预应力混凝土结构在分析预应力效应时，可以视为预加力和混凝土压力相平衡的自锚固体系，把预应力钢筋作为施加在混凝土结构上的外荷载进行等效计算.

对于梁端的等效荷载，如图2（a）所示，根据力的分解求得：

式中：Ny为梁端的轴力；Qy为梁端剪力；My为梁端弯矩；Py为预应力钢筋有效张拉力；e为梁端预应力钢筋的偏心距；θ 为Py与水平轴线的夹角.

预应力在梁体内折线布置时，可以将其等效为作用在梁体上的集中荷载；在梁体内直线布置时，可以将其等效为作用在梁体上的力矩；在梁体内曲线布置时，可以将其等效为作用在梁体上的均布荷载，如图2所示.

图2 等效荷载Fig.2 Equivalent load

2.2 等效荷载的剪力滞效应

梁端的等效荷载轴力Ny作用于梁端形心，剪力Qy作用在支座上，所以两者均不产生剪力滞效应. 只有等效荷载梁端弯矩My能够产生剪力滞效应. 作用于跨中的预应力钢筋，无论采用何种方式布置，均会产生剪力滞效应.

对于图2中简支箱梁布束方式，根据等效荷载的大小和梁端的约束条件，可以求得预应力钢筋在各种布置形式中考虑剪力滞效应的应力解.

1）预应力钢筋直线布置时，在等效荷载梁端弯矩下的应力解为：

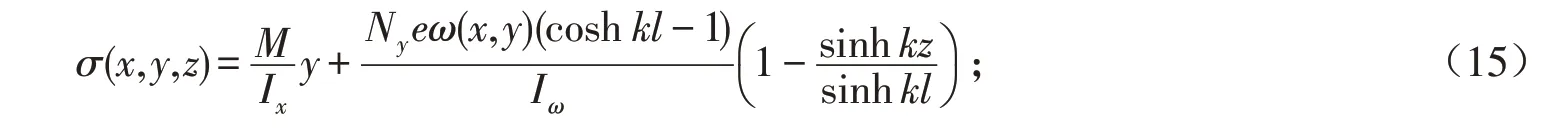
2）预应力钢筋折线布置时，在等效荷载跨内集中力下的应力解为：当0 ≤z ≤a 时，

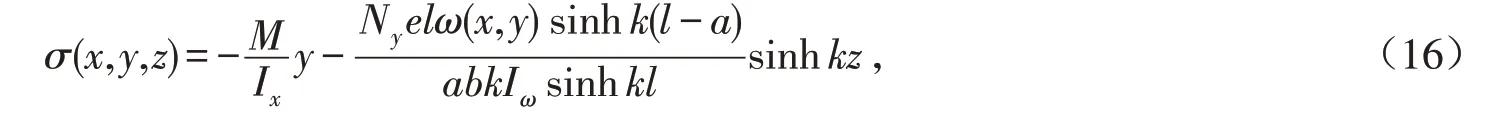
当a ＜z ≤l 时，

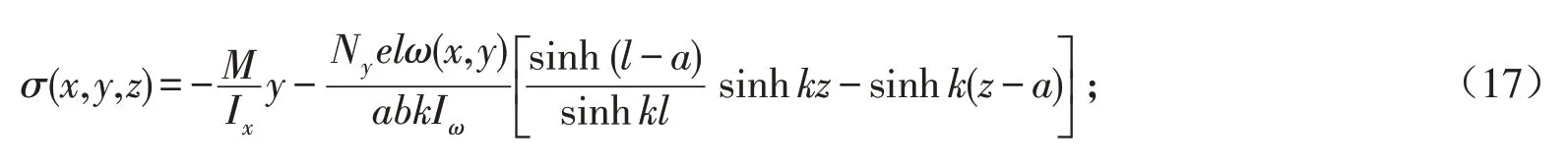
3）预应力钢筋曲线布置时，在等效荷载跨内均布力下的应力解为：

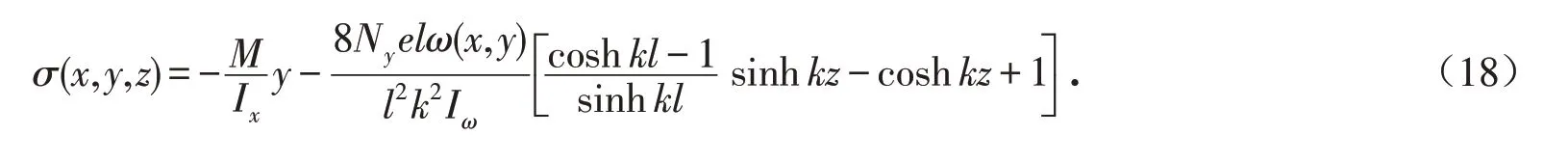
在实际工程中，预应力钢筋会直线、折线和曲线同时布置，并且存在锚固偏心距，此时在求解考虑剪力滞效应的应力时，需根据叠加原理求解.

3 算例

3.1 基本参数

某一预应力混凝土简支箱梁桥，跨度为50 m，材料弹性模量为E=3.1×104MPa，泊松比为μ=1 6，横截面尺寸如图3（a）所示. 预应力钢筋采用标准抗拉强度为1860 MPa，单束4根12-φj15.2 钢绞线，假设扣除预应力损失后的有效应力为1116 MPa. 预应力钢筋在梁体内的分布情况如图3所示.

图3 梁体预应力钢筋分布（单位：m）Fig.3 Distribution of prestressed reinforcements of beam

3.2 预应力剪力滞效应

根据梁体内预应力的分布形式，首先计算每束预应力钢筋的等效荷载，然后利用式（15）～（18）分别计算每种布束形式下考虑剪力滞效应的截面应力，再通过叠加原理求得截面总应力. 为了验证本文计算结果，采用ANSYS中的SHELL63壳单元对该简支箱梁建立有限元模型，并施加等效荷载. 计算求得跨中截面顶板和底板的纵向应力和梁轴向顶板、底板与腹板相交处的纵向应力如图4所示.

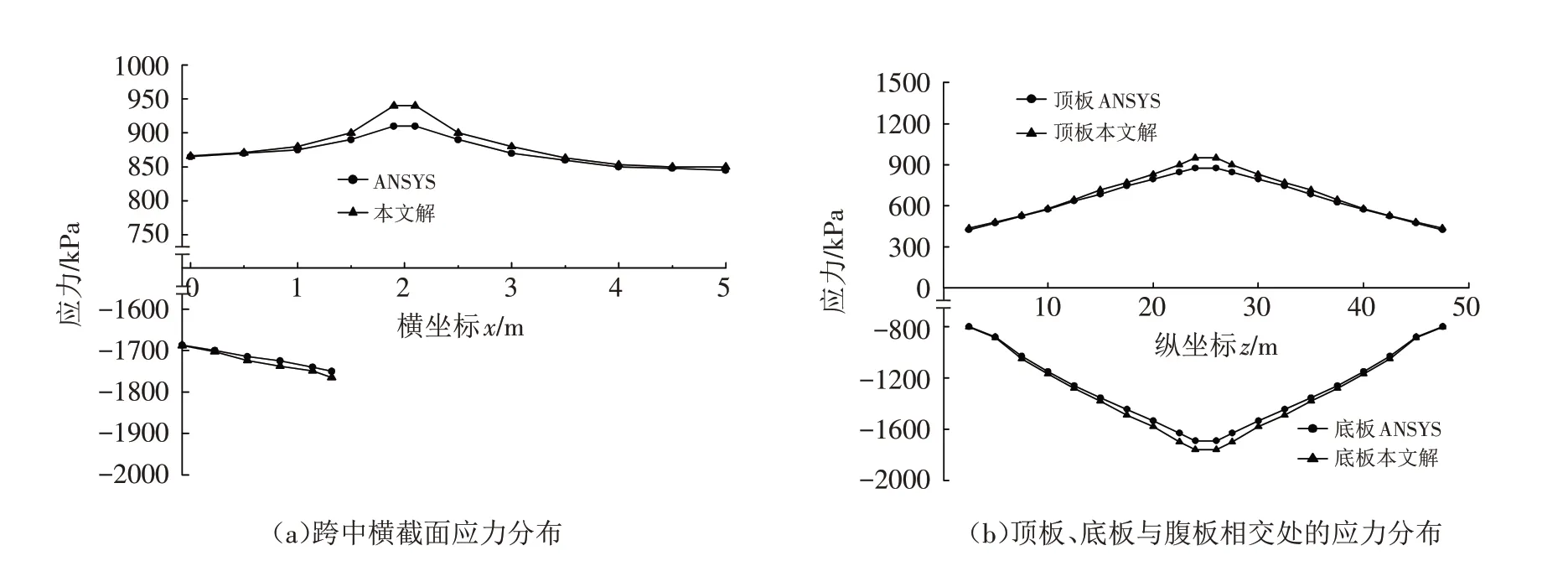
图4 应力分布Fig.4 Stress distribution

从图4可以看出，按照本文方法求得的应力解结果和ANSYS计算结果基本吻合，验证了本文理论解析解的合理性. 同时在预应力混凝土简支箱梁中，跨中截面顶板、底板与腹板相交处应力最大，剪力滞效应最明显.

4 高速铁路简支箱梁剪力滞效应分析

在我国高速铁路桥梁建设中，标准跨度为24 m和32 m的预应力混凝土简支箱梁被广泛使用［20-21］，在分析预应力作用下剪力滞效应时，箱梁基本尺寸如表1所示.

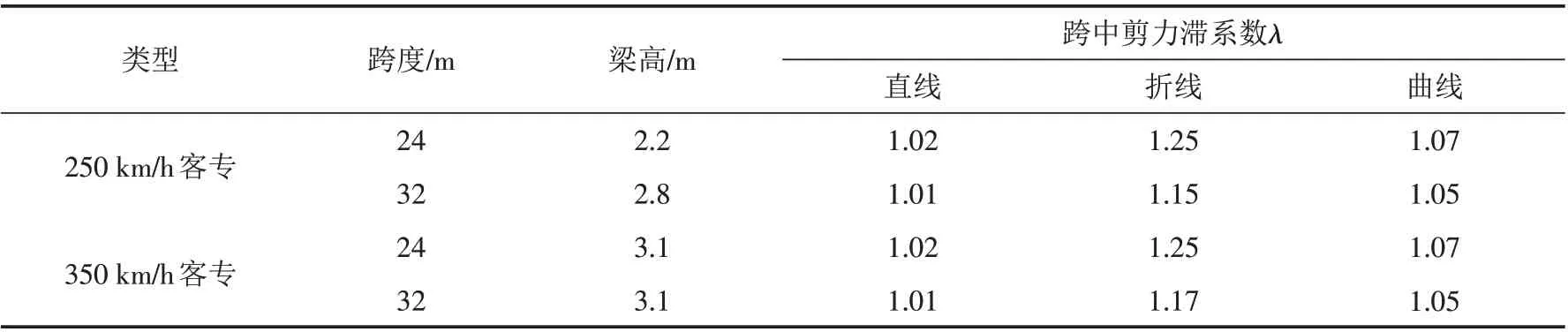
表1 标准跨度简支箱梁桥剪力滞系数Tab.1 Shear lag coefficients of standard span simply supported box girder bridges

一般用剪力滞系数λ 来描述箱形梁中剪力滞效应对弯曲正应力的影响，λ=σ σˉ，其中σˉ为按初等梁理论所得正应力，σ 为考虑剪力滞效应所得正应力.

对于简支箱梁桥，越靠近腹板位置，顶板和底板的纵向应力和剪力滞系数会越大，同时简支梁跨中截面是应力最大处，故本文分别列出了在直线、折线和曲线布束下跨中截面顶板和腹板交接处的剪力滞系数. 从表1可以看出，对于上面4种预制箱梁，预应力钢筋折线布束方式对梁体剪力滞效应影响最大，最大剪力滞系数为1.25；预应力钢筋直线布束对梁体剪力滞效应影响最小，剪力系数基本接近1；预应力钢筋曲线布束对梁体剪力滞效应影响在直线和曲线布束之间.

5 结论

本文主要对预应力简支箱梁进行了剪力滞效应分析，得到以下结论：

1）将预应力钢筋作为施加在混凝土结构上的外荷载进行等效计算，以附加挠度作为分析剪力滞效应的广义位移，基于能量变分法，建立了预应力作用下的剪力滞效应解析解.

2）通过ANSYS有限元软件中的SHELL63壳单元对一简支箱梁计算，求得的应力解和本文解析解计算结果基本吻合，验证了本文理论解析解的合理性.

3）通过对高速铁路标准跨度简支箱梁计算得出，预应力钢筋折线布束方式对梁体剪力滞效应影响最大，曲线布束对梁体剪力滞效应影响次之，直线布束对梁体剪力滞效应影响最小.