非对称二次随机系统的稳态响应

郭换芳， 刘 迪， 郭 蓉

（1.山西大学数学科学学院，太原 030006； 2.太原科技大学应用科学学院，太原 030006）

雅可比椭圆函数由于其在非保守系统的理论解方面具有较高的精度和一定的可行性吸引了越来越多的注意［1］. Barkham与Soudack［2-3］首先使用雅可比椭圆函数来分析确定性Duffing系统的近似解. 之后，一些学者发展了这类系统近似解的各种椭圆方法，如：椭圆谐波平衡法［4］、椭圆Krylov-Bogoliubov［5］和椭圆Lindstedt-Poincare法［6］等. Coppola［7］提出了相应的基于椭圆函数的确定性平均法，用该方法研究确定性系统的动力学行为具有更高的精度. 近年来，该方法得到了进一步的发展，Okaba与Rakaric［8］改进了基于椭圆函数的确定性平均法，将解表示为雅可比椭圆函数，用来研究具有各种弹簧特性系统的动力学行为.

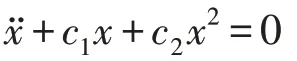
然而，在实际工程和自然界中不可避免地存在各种各样的随机扰动，如湍流、风浪、强地震激励作用等.随机扰动的存在可能会破坏系统结构，对系统的动力学行为产生不可预测的影响. 因此，研究随机扰动下系统的动力学行为具有重要的科学意义和广阔的工程应用前景. 对于Duffing系统随机情形，Tien等［14］提出了基于椭圆余弦函数的随机平均法，郑丽文等［15-16］改进了雅可比椭圆函数的随机平均法，并将其应用于高斯白噪声与有界噪声激励下的随机响应预测.

目前，对于二次非线性系统随机情形下的分析较少. 本文用基于改进的雅可比椭圆函数的随机平均法研究高斯色噪声激励下二次非对称随机系统的稳态响应，建立与求解相应的FPK方程从而得到关于幅值的稳态概率密度. 通过具体实例，利用Monte Carlo 数值模拟验证方法的有效性，进一步分析了参数变化对系统稳态响应的影响，给出相关结论.

1 二次非对称随机系统

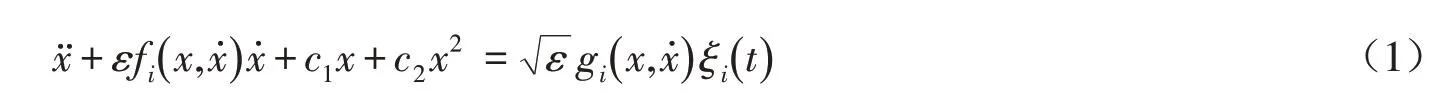
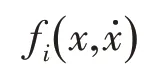
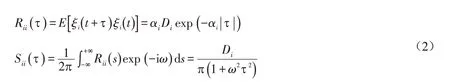
其中：αi和Di分别为色噪声的带宽和激励强度；ω 和τ 分别为频率和相关时间.

2 基于雅可比椭圆函数的随机平均方法

忽略阻尼项和随机项，系统（1）式退化为相应的保守系统

系统的总能量为

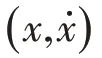
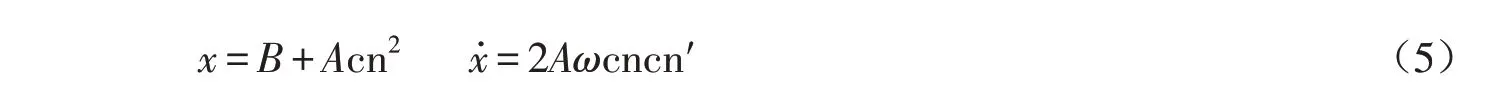
图1 不同线性刚度系数下系统的势函数，c2=1.0Fig.1 The potential functions of the system under different linear stiffness coefficients，c2=1.0

将（5）式关于时间t 求导并代入（3）式中，有

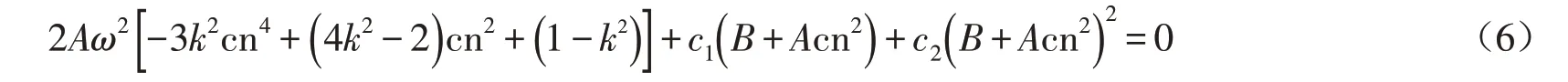
合并同类项，得到

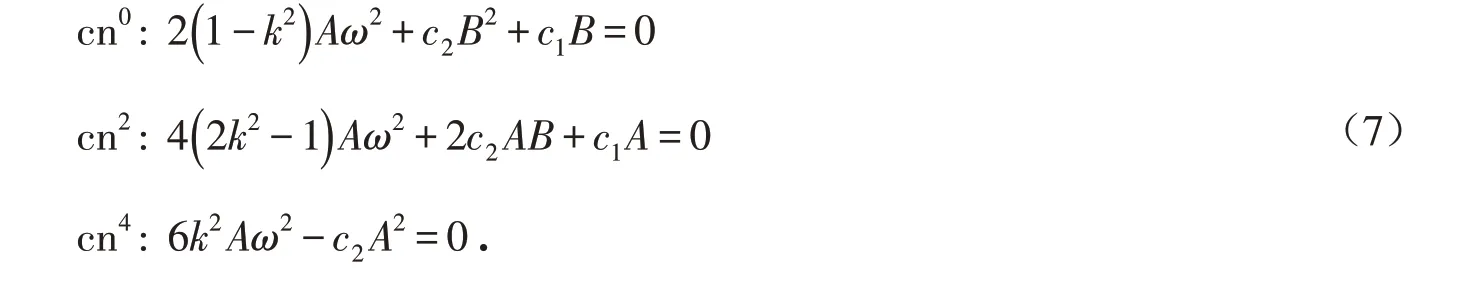
解上述方程，得到

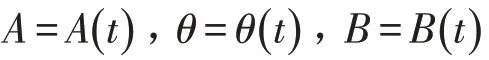
比较方程（9）式和（5）式中ẋ，下列关系式成立

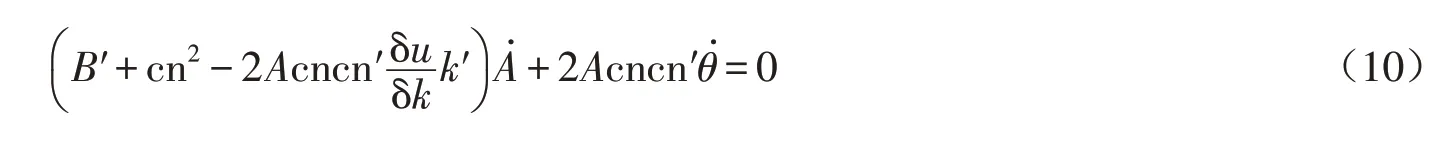
其中：B′=∂B ∂A k′=∂k ∂A .

对（5）式中ẋ关于时间t 求导，有

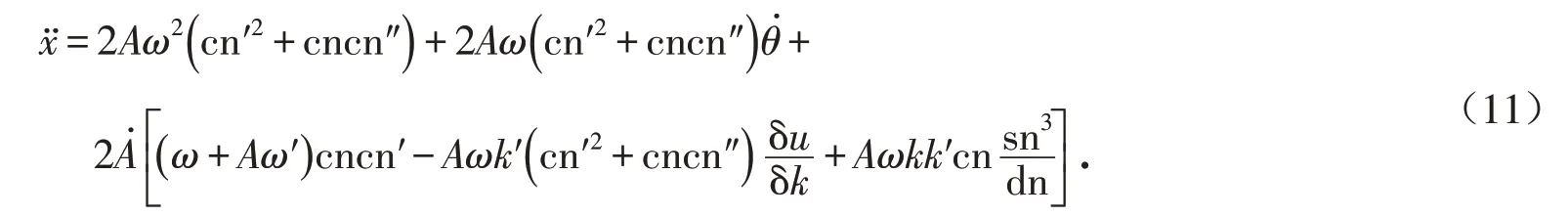
将（11）式代入（1）式并应用（6）式，得到另一个关系式

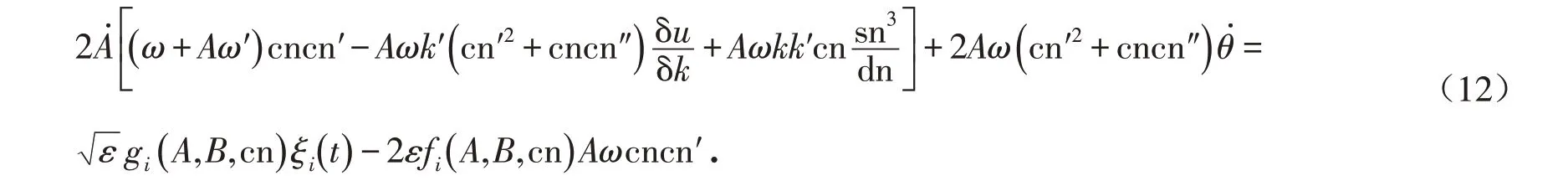
令

将

（10）式和（12）式代入（13）式，结合（10）式，我们有

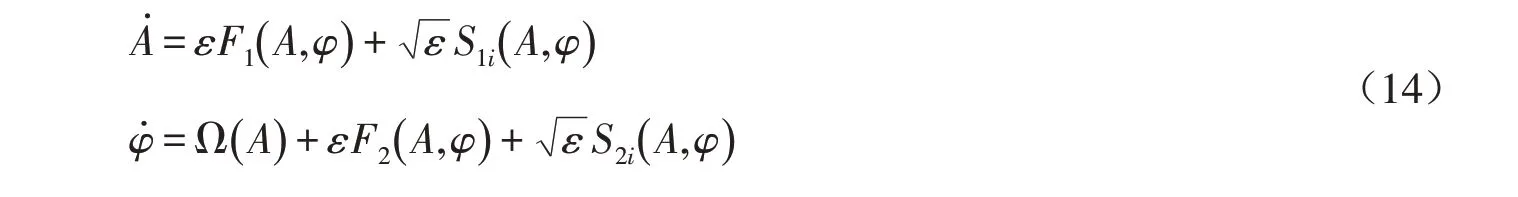
其中

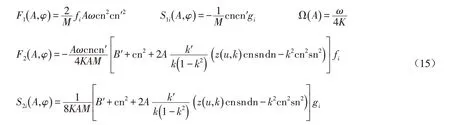
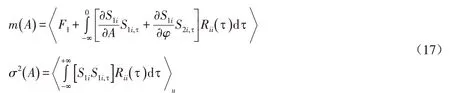
将（14）式、（17）式代入（16）式，对时间进行平均，表达式可转化为周期式，计算出平均漂移系数和扩散系数，对应于平均伊藤随机微分方程（16）式关于幅值A 的FPK方程为

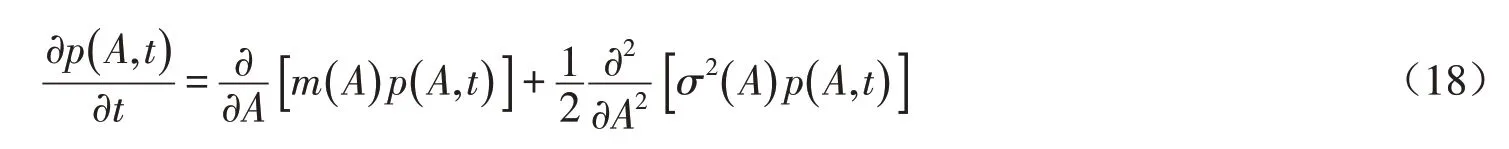
式（18）中令∂p ∂t=0，求解FPK方程，得到幅值的平稳概率密度函数

其中：C 为归一化常数. 根据（4）式可以进一步得到关于速度和位移的联合稳态概率密度及各自的边缘概率密度（da指对幅值A积分，避免与积分上限A表示重复，用a表示积分变量，重复并不影响结果）.

3 数值结果及分析

将变换（5）式代入（20）式中，对应于（15）式得到

利用（17）式并结合椭圆函数的傅里叶展开可以得到相应的平均漂移系数和扩散系数

其中：mi(i=0,…,4)分别为E和K的函数，我们很容易可以得到关于幅值的稳态概率密度.

图2～4给出了幅值的稳态概率密度曲线，据此来分析系统参数和噪声强度的变化对系统稳态响应的影响，其中线条（FS）表示理论结果，符号（MC）表示原系统的Monte Carlo数值模拟结果. 从图中可以看出近似解析解与原系统Monte Carlo数值模拟结果相吻合，表明基于雅可比椭圆函数的随机平均法可以有效地求解高斯色噪声激励下二次非对称随机系统的稳态响应.

在实际中噪声强度对系统的影响是不可忽略的. 图2 给出了不同噪声强度下幅值的稳态概率密度曲线. 观察可以看出，当增大噪声强度D 时幅值A 的稳态概率密度曲线的峰值逐渐减小，并且峰值的位置逐渐右移，说明增大噪声强度能够增强系统的稳态响应.

图3给出了噪声相关时间τ对系统稳态行为的影响. 观察可以看出，增大相关时间（即减小噪声带宽α）时，幅值A 的峰值逐渐增大，峰值的位置逐渐左移，说明增大相关时间τ，系统的响应逐渐减弱.

图2 不同噪声强度下系统的稳态概率密度，c1=6.0,c2=1.0,τ=1.0,ε=0.01Fig.2 The steady-state probability densities of the system under different noise intensities at c1=6.0,c2=1.0,τ=1.0,ε=0.01

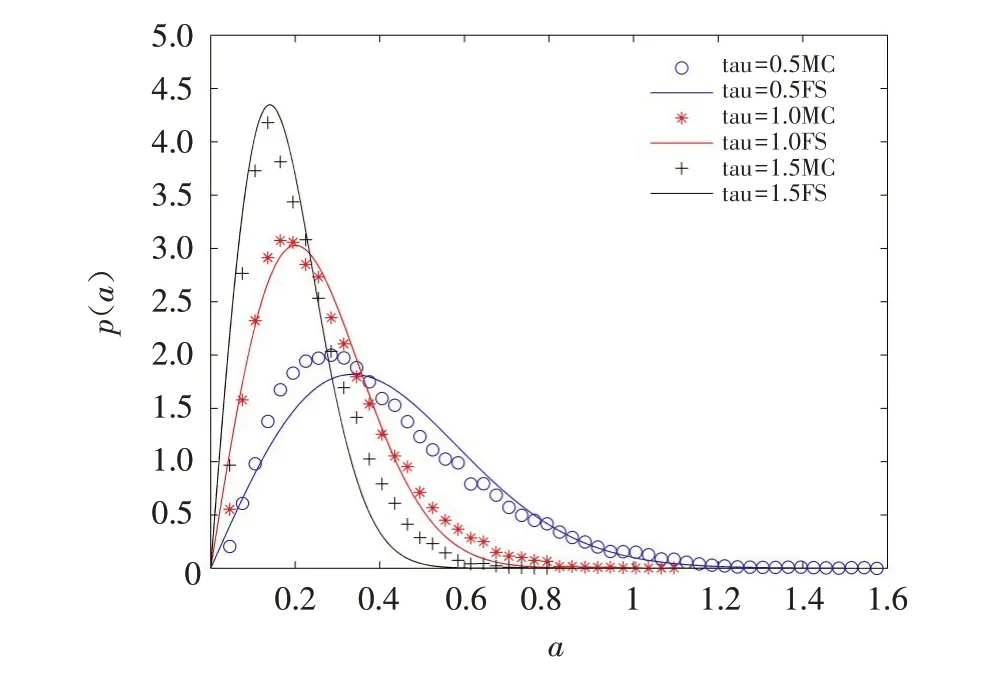
图3 不同相关时间下系统的稳态概率密度，D=0.2,c1=6.0,c2=1.0,ε=0.01Fig.3 The steady-state probability densities of the system at different correlation times，D=0.2,c1=6.0,c2=1.0,ε=0.01

最后图4给出了不同线性刚度下对系统稳态概率密度的影响. 可以看出，在不同线性刚度下系统表现出不同的动力学行为，当增大c1时，幅值A 的峰值逐渐增大，峰值的位置逐渐左移，这就表明，线性刚度的增大会减弱系统的稳态行为.

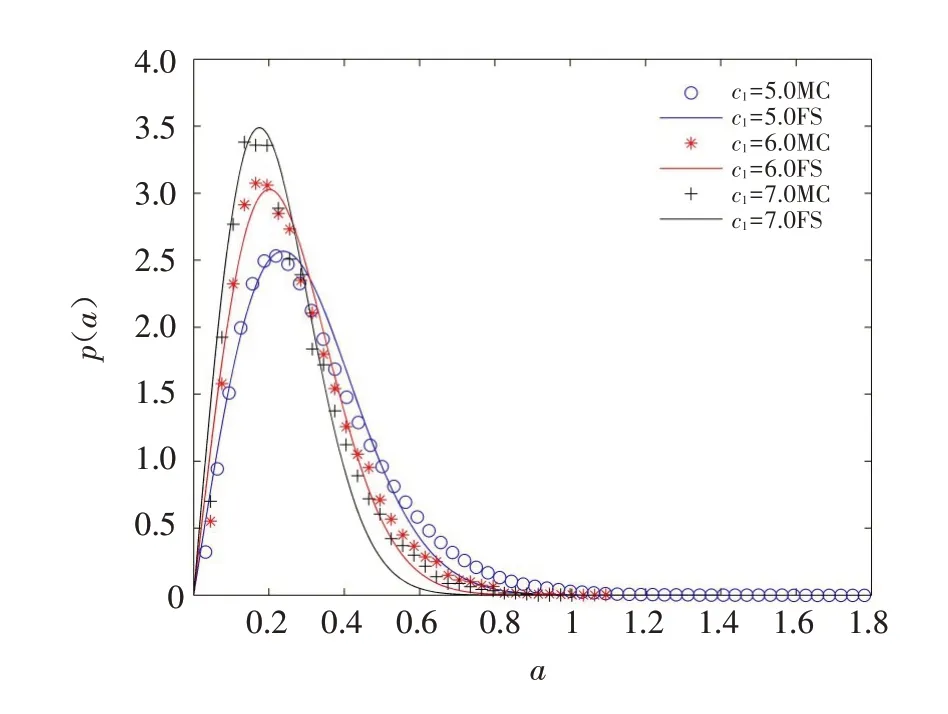
图4 不同线性刚度下系统的稳态概率密度，D=0.2,c2=1.0,τ=1.0,ε=0.01Fig.4 The steady-state probability densities of the system with different linear stiffness，D=0.2,c2=1.0,τ=1.0,ε=0.01

4 结论

本文探讨了高斯色噪声激励下二次非对称随机系统的稳态响应. 引入雅可比椭圆函数变换，应用随机平均法，得到幅值的伊藤随机微分方程，并建立与求解相对应的FPK方程，导出幅值的稳态概率密度的解析解. 通过一个典型的例子，将理论结果和Monte Carlo 数值模拟结果比较，验证了解析解的有效性. 结果表明，不同的噪声强度、相关时间和线性刚度对系统的随机响应有一定的影响，具体表现为噪声强度的增大会增强系统的稳态响应，而相关时间和线性刚度的增大则会减弱系统的稳态行为.