一种改进的稀疏表示超分辨率重建方法

李冠葳

（四川大学计算机学院，成都610065）

0 引言

在当今社会，随着科技的进步和发展，人们对图像质量的要求也随之增高，图像分辨率作为图像质量的一种重要评价方式，有两类方法可对其进行提升，其一是提高硬件设备的质量，采用提升硬设备质量的方法会提高成本，不利于推广使用；另一类方法是图像超分辨（Super Resolution，SR）重建技术，该方法通过一定的算法从低分辨率图像重建出高分辨图像[1]，图像超分辨率技术相较提高硬件设备的方法成本低，效果好，应用领域广泛，可用于军事侦察、医疗图像等领域，为解决这一问题提供了有效的解决方式，因此一直是一个研究热点。

现有的超分辨技术目前总的来说，可分为三大类：（1）基于插值的方法[2-4]；（2）基于重建的方法[5-8]；（3）基于学习的方法[9-10]。其中，基于插值的超分辨技术是最早提出的，也是最容易实现的超分辨技术，这类算法复杂度较低，通过相邻像素的信息来得到待插值像素的值，从而实现图像的超分辨。主要有三种方式，其中双立方插值是效果最好且使用最多的，它通过采用三次函数作为插值核，来求得待求像素值。但这类算法没有考虑边缘信息的方向性，不能较好地处理图像边缘及纹理信息，因此，存在一定的锯齿现象且细节模糊。Stark等[11]人在集合理论的影响下提出凸集投影法，由此基于重建的超分辨算法也出现了，基于重建的方法主要通过从输入的多帧图像中提取出可用信息，但这种方法结合先验知识不足，在一些场景不能表现出很好的效果，同时，在重建尺度较大时效果较差，边缘细节模糊。因此，基于学习的超分辨技术随之产生，很好的解决了这些问题，该类方法依靠一个事先建立的图像训练库对待复原的单幅低分辨率图像进行超分辨率重建。从外部训练集中学习得出高低分辨率图像间的对应关系，再利用这个模型重建出高分辨率图像，提高图像分辨率，更好的结合先验知识。其中，Yang等[12]受压缩感知理论的启发，首次将其应用到图像超分辨领域，由此一种新的算法被提出，即基于稀疏表示的图像超分辨方法，算法在字典训练阶段进行联合训练得到两个对应的具有相同稀疏系数的高低分辨率字典对，高分辨率字典对目标高分辨率图像进行重建，同时由低分辨率字典与输入图像计算得出重建所需的稀疏系数。该算法通过冗余字典构建较为全面，因此得到的高分辨率图像具有更多的边缘和纹理细节。综上，本文提出一种改进的稀疏表示的超分辨率重建算法，在字典训练阶段将高频信息分解，分别进行训练得到主要高频字典和残余高频字典，针对不同的高频信息对图像进行重建，并针对会对评估造成变差的细节信息，采用一种改进的迭代反投影法进行全局约束，从而得到最终的高分辨率图像。

1 本文算法

图像超分辨率重建算法具体包含字典学习和图像重建两个部分。考虑到重建图像与原图像之间存在误差，为了获得更好的重建效果，本文算法在字典学习阶段将高频信息提炼为主要高频信息和残差高频信息，在纳入残余图像的考虑下，通过字典学习训练出字典对。然后利用该字典重建低分辨率图像，并得到其主要高频信息和残差高频信息，将二者融合从而获得重建后的高分辨图像。

1.1 字典学习

本小节主要介绍进行字典训练的具体过程，并得到主要高频字典和残余高频字典。在字典学习阶段通过引入稀疏表示，采用OMP求解稀疏系数，通过基于学习的方法构建字典。在对字典进行训练时，需要对高低分辨率图像提取特征及分块处理，再利用K-SVD过完备字典训练算法构造字典。

（1）训练样本及特征提取

首先，对已有的高分辨率图像HORG进行预处理作为训练图像，在下采样算子等的作用下获得低分辨率图像LLF，进一步由双三次插值得到相同尺寸的高分辨率低频成分图像HLF，将二者进行差分得到差值图像HHF，对其进行特征提取。从低分辨率图像中提取其边缘特征，通过4个滤波器提取低分辨率图像的梯度信号，4个滤波器依次定义为：

对HLF进行滤波得到相应地4个特征向量，合并后得到最后的特征向量。

（2）主要字典训练

在第一重字典训练的时候，通过高低分辨率图像块得到低频主要字典LMD和高频主要字典HMD。由（1）中提取到的图像特征块构成高低分辨率图像训练库，由高低分辨率图像块构建高分辨率训练集与低分辨率训练集。继而通过K-SVD算法训练交替地求得低频主要字典，对其进行求解，约束方程为：

求解上述方程式，若Q为行满秩矩阵，则方程解可被表示为：

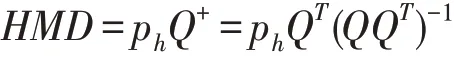
其中，ph和Q分别表示由和所组成。

（3）残余字典训练

利用（2）中训练得到的LMD和HMD对HLF重建得到HMHF，与HHF差分可得HRHF。将重建后图像HMHF与低分辨率图像HLF进行融合，引入HTMP，将HRHF和HTMP经过特征提取后的图像进行训练图像块提取，得到训练库，然后利用K-SVD全局字典学习对残余字典训练，训练过程与（2）相同，进而得到残余字典对LRD和HRD。

1.2 超分辨图像重建

首先，利用已知的LMD与HMD字典对重建输入图像，获得目标高分辨率图像，发现重建后的高分辨率图像对比原始高分辨率图像仍缺失一些细节，对于这一情况，本文对残余高频信息进行字典训练，进一步提取高频细节，用残余稀疏字典对目标高分辨率图像进行重建。这样得到的高分辨率图像包含两类细节信息，一类是可以确定的低分辨率图像降质后的位置，另一类不可确定的需进行估计的位置信息。因此，本文算法中加入迭代反投影算法进行全局约束，利用输入的低分辨率图像对高分辨率图像进行全局约束进行修正。

迭代反向投影（IBP）算法的核心思想是结合图像序列插值，通过估计得到初始高分辨率图像，然后经过已知降质模型得到初步估计的低分辨率图像。将其与输入低分辨率图像进行误差计算，若在允许误差范围内，则初始高分辨率图像就是目标高分辨率图像。否则将误差投影到初始高分辨率图像上，重复上述迭代，直到误差收敛到可接受范围内或达到了设定的最大迭代次数，估计得到目标高分辨率图像。Rasti P等[13]提出了一种改进的迭代反向投影算法，通过在每次迭代的过程中加入双三次插值和双三次下采样进行处理，得到效果更好的目标高分辨率图像。本文将重建出的高分辨率图像进行退化处理，然后将退化后的图像与输入的低分辨率图像差分，并在原始高分辨率图像上叠加残差图像的作用，重复上述过程直至收敛，以期望获得具有更丰富细节的高分辨率图像。

具体的图像重建算法流程如下：

（1）输入低分辨率图像HTl进行双三次插值得到HTh，用1.1小节的方法对低分辨率图像进行特征提取，并进行分块表示得到集合

（3）根据高低分辨率字典之间的一一对应关系可得到高频特征图像块，则高分辨率主要高频图像HMHF可表示为：

其中，Rk为在图像中提取位于位置k的图像块的算子。

（4）将高分辨率主要高频图像HMHF和低分辨率图像HTl相加得到重建后主要高频成分高分辨率图像HTMP。

（5）对主要高频成分高分辨率图像HTMP进行分块得到集合，求解在残差字典的低分辨率字典上的稀疏表示

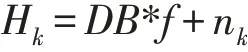
其中，Hk表示第k次迭代所得的模拟低分辨率图像，D表示下采样算子，B表示模糊算子，nk表示额外的噪声。

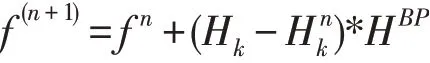
其中，fn表示第n次迭代估计的高分辨率图像，反向投影算子由HBP表示，Hnk表示估计的高分辨率图像fn通过降质模型得到的低分辨率图像。

2 实验结果及分析

本节对算法进行实验与评估。与双三次插值算法和稀疏表示法进行比较，分别对其进行实验。在本次实验中，采用输入图像以及其下采样5倍的图像作为训练集，在进行字典训练时，字典大小设置为128，设定图像块为3×3，在进行稀疏重建时，重叠像素为1。采用峰值信噪比（PSNR）和结构相似度（SSIM）比较各算法结果，达到客观评价，其计算方式如下：

式中，M、N代表图像尺寸，Yi,j与Ŷi.j分别代表初始图像和结果图像，μx和μy为图像平均亮度，σx与σy代表方差，σxy为二者协方差。峰值信噪比为图像峰值信号和背景噪声之间的比值，重建图像质量与其正相关，PSNR值越大，即重建效果越好。结构相似度考量的是测试图像与参考图像之间的相似性，SSIM值介于0和1之间，越接近1则表明重建图像与参考图像越相似，重建效果越好。

图1 实验图像Girl的三种方法的重建图像

从图1可以看出，双三次插值重建的结果图像存在明显的模糊现象。Yang算法和本文算法能够较好地恢复得到图像的细节，从Girl图像可以看出，与插值方法和Yang算法相对比，本文算法对脸部边缘轮廓的重建更加清晰，颜色较为统一，视觉效果更好。

通过PSNR和SSIM比对实验进行客观评价，如表1所示，体现了不同方法下对测试图像进行重建得到的PSNR值和SSIM值。

表1 不同算法PSNR和SSIM结果对比

由表1可以看出，应用本文算法重建图像的PSNR值SSIM值高于Yang等算法，表明本文提出的算法获得了较好的重建效果。如Girl图像的重建效果，双三次插值算法对该图像的PSNR值最低为34.859，Yang算法所的PSNR值也低于本文的峰值信噪比0.561dB。对比SSIM值，本文算法所得的SSIM值为0.9298，相较于其他两种算法效果更好。因此从实验结果可以看出，利用本文提出的方法达到了较好的效果，实验结果表明本文提出的算法优于其他算法。

3 结语

本文在基于稀疏表示的超分辨率重建框架下，在字典训练阶段将高频信息分解为主要高频信息和残余高频信息，分别进行字典训练，通过双重字典对低分辨率图像进行重建，以获得具有更丰富细节的重建图像，在重建得到高分辨率图像后，为了进一步修正图像，引入一种改进的迭代反投影法对图像进行全局约束，获得了更好的效果。客观上印证了结论，本文提出的改进算法在各项指标评价上表现地更好，使图像的重建质量得到了提高。