并行绘制系统中基于随机森林的预测算法改进

郭赛赛，李君怡

（四川大学计算机学院，成都610065）

0 引言

随着计算机硬件及软件技术的不断发展，计算机图形学与虚拟现实的应用场景越来越多，特别是在科学、工程、医学、生物学、娱乐业等领域得到了广泛应用。一些应用领域如科学、VR游戏等，为了得到最佳的效果，通常会使用超分辨率的巨大屏幕或者较高的刷新频率，增加真实性、提升用户体验。其中需要的图形计算能力、输出帧率对单一绘制系统提出了严峻挑战。为了解决这个问题，并行绘制技术被提出，通过将一个大任务分解成多个子任务同时处理极大地提高了绘制效率。由于目前大部分的实时绘制算法如De⁃ferred Shading、Ray Tracing都是基于屏幕空间，因此本文采用基于屏幕空间的负载划分来适应大多数绘制算法。本文用绘制时间来代表负载，目的是使得几个子屏的绘制时间相当，以达到较好的负载平衡。如果在每一帧绘制任务被划分后可以给出一个相对准确的负载预测结果，系统就可以根据这个结果去调整划分方式，从而使得不同绘制区域的负载达到均衡，提高绘制速度。

本文将这个预测过程用机器学习的思想来实现，通过机器学习模型学习已有的数据，在新的一帧画面到来的时候，将画面转换为训练模型用到的数据格式，用模型做出预测，并根据这个预测结果去调整划分方式。为了提高预测效率、并较好处理复杂绘制场景中的高维数据，本文选取Breiman[1]提出的随机森林作为预测模型。

随机森林中每棵决策树[2]给出的预测结果由测试样本所落入的叶子节点中的数据的平均值决定，这些数据的熵越小，纯度越高，预测越准确。为了将训练集划分得足够纯，本文在构建随机森林的时候，采用最小化残差平方和（Residual Sum of Squares，RSS）[3]来确定每次节点划分所用的特征与位置。但由于随机森林中用来预测的一组叶子节点中的数据并不完全相同，因此，每棵树给出的预测结果准确度也不同，而原始的随机森林均值预测法并未考虑这个差异，从而使得最终的预测结果有一定偏差。

为了解决数据差异带来的预测偏差，通常的解决方案是为每个预测用叶子节点加置信度，作为最终的预测权重。置信度的计算方式有很多，针对RSS划分决策方法，每个叶子节点置信度通常用其所包含的数据方差来计算，即，方差越大，置信度越低。加入置信度后的随机森林的预测能力会有一定程度的提升，但面对一些其他问题，如划分得到的实际叶子节点空间较大使得落入的测试样本与其中包含的训练数据差异较大时，即使该节点中的数据方差很小，依然很难给出一个相对准确的预测结果。为了解决这个问题，本文提出根据拟合度判定函数来用路径上的节点代替部分叶子节点做预测的方法。

1 算法实现

1.1 算法思想

随机森林通过自助法（bootstrap）重采样技术[4]，从大小为N的原始训练样本集中有放回地重复随机抽取N个样本生成新的训练样本集合，构成一棵决策树，将该过程重复M次，得到由M棵决策树组成的随机森林。在解决分类问题时，一个测试样本最终得到的预测结果是根据所有决策树给出的投票结果决定的。而对于回归问题，随机森林给出的预测结果是每个决策树给出结果的平均值。本文目的是对负载时间做预测，因此属于回归问题。

用路径上的节点而非叶子节点做预测依然是以随机森林为基础。每棵决策树是通过不断选定一个特征的一个位置向下划分，最终会将决策树的整个数据空间划分成一个个独立的小的子空间，一个叶子节点代表了一个子空间。决策树在向下划分过程中，通常需要为它设定合适的停止划分条件，避免最终将每个训练数据单独划分到一个叶子节点得到过拟合[5]的决策树。本文在选取划分停止条件时主要考虑两个问题：节点中数据量与节点中数据纯度。数据量太多预测准确性较低，太少容易过拟合，最终根据实验结果确定了一个最大数据量，当节点中数据量小于这个值就停止划分。划分的目的是使决策树节点中的数据越来越纯，因此，如果这些数据的值已经全部一样，也就是纯度已经达到最高后也会停止划分。这两个停止条件可能会带来的两个问题分别是：叶子节点中较少不同数据代替整个节点空间做预测；用相同的数据代替整个节点空间做预测。这两个问题本质上与过拟合很相似，都是训练数据不足以准确表达出其所代表的整个空间的特征。而随机森林在构建过程中通常不考虑过拟合问题，因此，面对这两个问题带来的预测误差，随机森林的均值预测法往往不能给出有效调整。

用路径上的节点代替叶子节点预测从根本上讲，就是通过增加预测用的数据量来解决过拟合的问题，这一过程可以看做是对随机森林做了“假”剪枝[6]。之所以是假的，是因为实际上并没有剪枝。测试样本从某棵决策树根节点一直向下走的过程中，本文会在每个节点通过一个布尔函数来判断这个叶子节点中的数据相对测试样本来说是否过拟合，如果结果为真，就不再继续往下，用停止位置的节点去预测，等于在该位置剪枝；否则，就继续向下直到到达叶子节点，等于未做剪枝。也就是说，对于走同一条预测路径的两条测试样本，可能有一条走到在路径中间就停止，而另一条会走到路径终点，也就是叶子节点，因此是“假”剪枝。

1.2 算法实现

原始随机森林在预测的时候，每条测试样本从进入一棵决策树根节点开始，就要根据当前节点的划分方式不断的去判断下一步是去左子节点还是右子节点，直到到达叶子节点。而将路径上的节点加入最后的预测时，这个过程也会有一些变化，具体算法流程如下：

（1）根据完整训练数据集D（d1，d2，…，dN）构建随机森林预测模型F（f1，f2，…，fM）；

（2）依次将测试数据集T中的每条样本t放入模型F（t初始是落入F中每棵决策树的根节点）；

（3）判断当前节点是否为叶子节点，如果否，执行步骤（4），否则，执行步骤（5）；

（4）判断当前节点是否存在过拟合风险，如果否，判断t下一步落入的节点，回到步骤（3），否则，执行步骤（5）；

（5）停止继续向下寻找节点，用当前节点作为对应决策树最终的预测节点；

（6）用每棵树最终给出的预测节点做负载预测。

1.3 细节描述

在本文提出的算法中，关键点在于如何判断一个节点中用来预测的数据相对于测试样本来说过拟合。这里面包含了两个点：用什么来表示拟合性；过拟合的标准怎么定。

通过对预测结果好坏不同的测试样本研究发现，它们预测结果的差异大小与用来预测它们的节点中的数据分布有很大关系。因而本文最终采用根据测试样本各维特征是否超出节点中数据特征范围来判断拟合性。拟合标准由实验结果确定。

这里以二维数据集为例做简单分析。如图1对于某个非叶子节点A，通过选定一个特征α的位置β，将A划分成了左右两个子叶子节点B、C。节点A划分前后的数据分布可能会出现图1中左右两种情况，这时如果一个测试样本P最终落入了两种情况下的同一个位置。可以发现，图2左中P是落入一堆数据中间，而图2右中P虽然落入叶子节点B中，但实际上与B中的数据有一定距离，甚至P离C中的数据反而更近。这个时候，同样都用B中的数据去预测P，两种情况给出的结果准确度肯定会有差异，而且可以猜测，图2左给出的结果应该更加准确。如果出现图2右的情况，用C节点做预测应该会优于用B节点，但随机森林的特性就是根据划分结果找到它以为最合理的预测节点，就是这里的B，因此将定位到的预测节点改为它的兄弟节点就与这个特性相冲突。这种情况如果出现在单棵决策树的机器学习模型上，它会认为当前模型过拟合，通常的解决方案就是剪枝，这里就是永久性的去除B、C节点，用A做预测。结合单棵决策树的剪枝策略，本文提出用路径上非叶子节点代替叶子节点做预测的方案。如果拟合度判定函数结果显示，A以后的节点相对测试样本来说过拟合，将停止在A节点，用A节点做预测。这里不做真正意义上的剪枝还有一个好处，若与B节点中数据相似的测试样本进入模型后，最终仍能到达B节点，而不是只能停在A。

图1

图2

根据数据分布特征，本文将拟合度判定函数f设定为与测试样本x超出所到节点中全部数据各维特征范围的数量K有关，当f（x）≥K时，即认为从当前节点开始，节点中的数据分布相对测试样本来说差异较大，因此，不适合用更底层的节点预测。

本文这种考虑路径上节点做预测的“假”剪枝方法在保持原有预测结果较好的样本准确度变化不大的同时，增加了对预测结果不好的样本的预测能力，最终提升了整体预测准确度。

2 实验结果

2.1 实验环境

PC配置：Intel Core i7-8700K 3.70GHz CPU，16G内存，NVIDIA GeForce GTX 1080显卡；

绘制系统：加入Light Linked List（LLL）算法[7]产生大规模动态光源光照效果、Screen Space Ambient Occlu⁃sion（SSAO）算法[8]优化绘制效果、Order Independent Transparency（OIT）算法[9]绘制场景透明物体；

实验数据：从绘制场景中多条漫游路径采集1，195，906条数据构成训练集，19，626条数据构成测试集。

2.2 实验结果

模型参数设置：

表1

数据集参数列表：

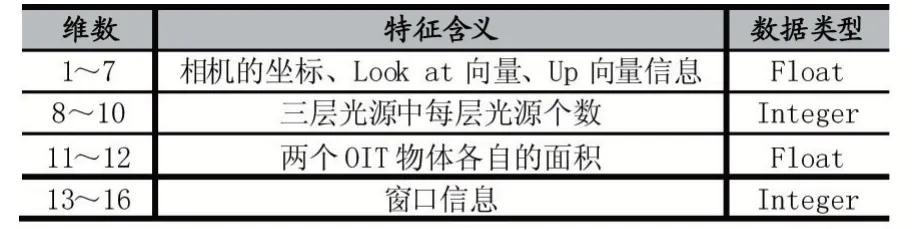
表2

已知数据特征共16维，因此，拟合度判定函数中允许样本超出维度数K的范围应在1～16之间。

本文采用均方误差（Mean-Square Error，MSE）[10]、R2Score（Coefficient of Determination）[11]两种回归算法最常用的性能度量方法来反映预测准确度。MSE越小说明预测越准确，R2Score越接近1说明预测结果越接近真实值。

为了验证本文算法的正确性并找到合适的K取值，实验一通过设置不同的K值，计算对应的MSE与R2Score值并与原始RF预测结果做对比。实验二、三分别对原始RF预测结果最好、最差的前10000条测试样本集Db、Dw进行测试，来验证该方法对预测理想的数据的预测能力保留，对预测不理想数据的包容。

总而言之,胫骨平台合并半月板损伤患者接受早期的胫骨平台骨折手术修复治疗,对损伤半月板进行修复,能够在一期就实现愈合,避免了骨折预后创伤性关节炎的发生,临床中效果比较突出,值得推广使用。

实验一：验证K取值对原始测试集预测结果的影响

已知K值的大小决定了最终用来预测的节点位置，为了得到相对较好的结果，本文通过实验验证了不同K值下预测结果的变化。图3中横轴代表不同K的取值，实线与虚线分别代表了对应K取值下的MSE与R2Score值。已知在原始均值预测方法下，该测试集的MSE为0.571698，R2Score为0.795982。由实验结果可知，当K取1～15之间的值时，改进后的算法预测能力都有所提升，而K的最佳取值为3。

图3

实验二：模型改进前后对数据集Db的预测结果对比

根据实验结果，原始RF对最好的前10000条数据集Db的预测结果为MSE等于0.038829，R2Score等于0.982161，而将K设置为3时，MSE等于0.0546641，R2Score等于0.974886，并且进一步验证了将K设置为1～16间的任何数后的预测结果都不优于原始RF，这说明对于已经学习到的数据来说，叶子节点可以给出更好的预测结果，也证明“假”剪枝中“假”的必要性。

实验三：模型改进前后对数据集Dw的预测预测对比

原始RF对最差的前10000条数据集Dw的预测结果为MSE等于1.08791，R2Score为0.671973，K=3时，MSE等于0.907903，R2Score等于0.726248，预测能力有一定提升。而通过将K设定为1～16之间不同的值，发现K取1时，预测结果提升最大，这说明对于没有很好学习到的数据，可能叶节点包含的数据及邻近的数据与测试样本的偏差更大，证明了“剪枝”的重要性。

3 结语

本文提出基于原始随机森林用测试样本预测路径上的节点代替叶子节点做预测的算法，在保持用原始随机森林预测较好的样本预测结果变化不大的同时，增加了对预测不好的样本的预测能力，并对该算法进行了实验验证，从结果可以看出该算法对模型预测能力整体有一定提升。