曲面纹理映射算法研究及实现

王浩杰

（四川大学计算机学院，成都610065)

0 引言

纹理映射（Texture Mapping）是计算机图形学中常用的一种技术，它被广泛应用在3D游戏开发，虚拟现实（Virtual Reality），三维真实感图形的生成和显示等领域中。各种各样复杂图形的渲染中也使用了纹理映射技术[1]。可以将纹理映射定义为：将纹理空间中的纹理图像映射到物体表面的过程。传统的纹理映射算法，大多数是基于平面的，很多工业造型物体表面比如汽车、飞机、花瓶等，都是由自由曲面或不规则多边形构成，这些物体的难以用参数表达式直接表示，因此也不能直接进行纹理映射，这也是纹理映射中的难题之一。针对这些难点，本文主要对参数曲面和不规则曲面之间的纹理映射算法进行研究。

1 纹理映射基本算法

映射（Mapping）是纹理映射中的核心问题，两个集合中元素中间的对应关系可以用映射来表示。而纹理映射可以认为是建立两个集合之间的映射关系。纹理空间用纹理图像的定义域空间表示，景物空间就是需要映射的三维物体表面。纹理映射中主要包含两个映射[2]：

假设点P1(x,y)是纹理图像上任一点的坐标，是三维景物表面上任一点的坐标，纹理图像到景物空间的映射就是确定三维景物表面上的点和纹理图像上的点之间的对应关系[3]，然后将纹理值赋给景物空间点，映射可以用下式表示：

景物空间到屏幕空间的映射：将景物变换为目标图像，通过取景变换将景物显示到屏幕上，即可得到最终的计算机图像。

根据纹理图像和景物空间之间的映射顺序，纹理映射可以分为：正向映射、逆向映射和两步法纹理映射。

1.1 正向映射

参数曲面纹理映射最开始采用的就是正向映射[4]的算法，也可以把它称为纹理扫描法（Texture Scan⁃ning）。参数曲面纹理映射关键是求出目标参数曲面的逆映射，但是一般参数曲面的逆映射难以确定，最开始采用的是一种递归分割的方法[5]，近似地建立了离散的映射关系，将纹理坐标和参数曲面坐标进行一一映射，确定纹理像素在景物参数曲面的位置和大小，再通过线性插值计算参数曲面上对应点的像素中心处的参数值。正向映射的优点是实现相对简单，缺点是映射过程中景物参数空间和纹理空间不能完全对应。正向映射过程如图1所示。

图1 正向映射

1.2 逆向映射

逆向映射技术是Blinn[6]提出来的，逆向映射是一个和正向映射相反的过程，逆向映射也成被称为屏幕扫描法（Screen Scanning）[7]。在逆向映射中，先将图像空间中像素I所表示的区域投影到景物空间区域S，然后将S区域映射到纹理空间；这里需要对纹理图像进行重采样，计算曲面空间坐标中心的像素值，然后将计算结果赋值给曲面空间。逆向映射算法在一定程度上改进了正向映射的缺点，实现了纹理空间和景物参数空间的完全对应。逆向映射也是纹理映射中应用较普遍的方法之一。

2 参数曲面的纹理映射

对于一些复杂的物体，其曲面一般是非线性的，难以直接参数化，不能直接对其使用纹理映射，但是可以借助两步法纹理映射技术[8]。其核心思想就是把原来的映射拆分为两个映射，这个过程需要借助一个中间曲面来实现，把纹理图像映射到简单的中间曲面的映射记为S映射，中间曲面到最终的景物表面的映射记为O映射[9]。用O映射和S映射的复合表示完整的映射，两步法纹理映射可以分为下面的两个步骤：

选定一个合适的中间曲面是两步法纹理映射的关键，一般来说，常见的中间曲面有球面、立方体表面、圆柱面和自由曲面，要想得到的一个比较好的纹理映射效果，选定的中间曲面需要贴近最终的目标曲面。选定中间曲面后，然后建立中间曲面到景物表面的映射关系。

2.1 二次曲面

先介绍简单的二次曲面的纹理映射。如果可以通过一些变换把纹理空间转换到参数空间，一些简单二次曲面的逆映射表达式，可以直接进行纹理映射[10]。但是对于复杂的高次参数曲面来说，参数曲面的逆映射求不出解析表达式，只能通过一些数值求解算法来离散求解它们的逆映射。简单的二次曲面，其纹理映射逆映射可以用它的解析表达式表示。

以圆柱面为中间曲面的参数表示，一个高为h，半径为r的圆柱面的参数表达式为：

以圆柱面为中间曲面的纹理映射的原理如图2所示：

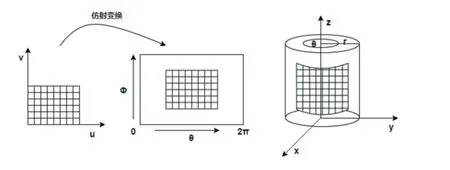
图2 柱面映射

2.2 Bezier曲面

常用的自由曲面有Bezier曲面[11]和B样条曲面，它们可以灵活的控制曲面的形状。基于控制点实现的自由曲面控制灵活，方便造型，易于拼接。参数曲面的解析表达式就是二维参数空间到三维空间的映射，利用其解析表达式能够方便实现纹理映射。

Bezier曲面的定义如下：设Pij(i=0,1,…,m;j=0,1,…,n)为( )m+1×(n+1)个控制点列，则m×n次Bezier曲面定义为：

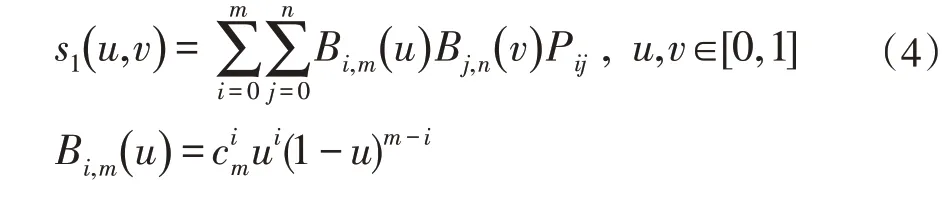
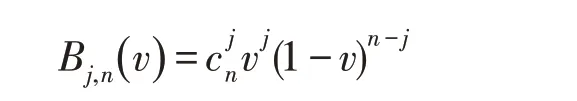
其中Pij是控制点，是Bernstein基函数。当n=m=3时，得到的双三次Bezier曲面如下：

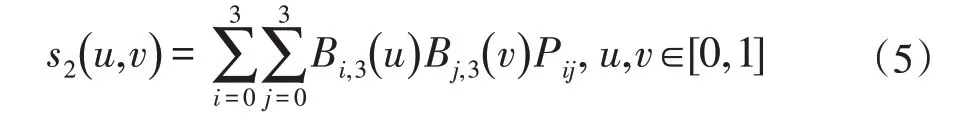
矩阵形式如下：

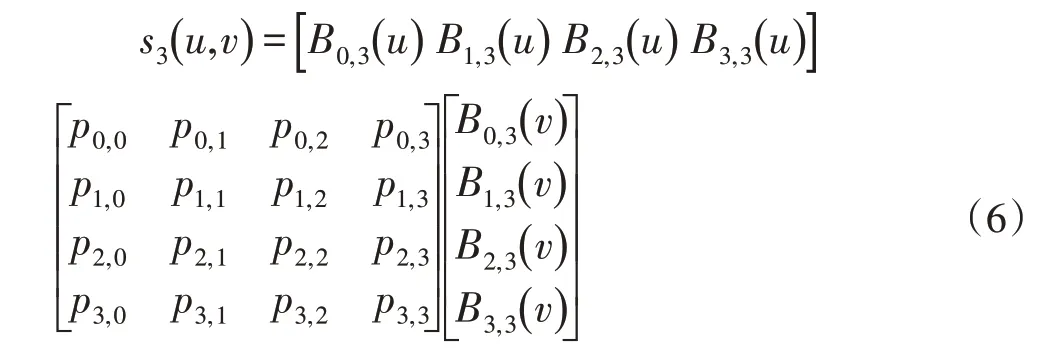
Pij(i=0,1,2,3;j=0,1,2,3)构成了参数曲面的控制点矩阵，一张双三次Bezier曲面片由16个控制点确定。由Pij组成的空间网格称为特征网格，曲面的形状受到特征网格中控制顶点的控制，通过调节控制顶点，曲面的形状也随之改变。双三次Bezier曲面如图3所示：

图3 双三次Bezier曲面

2.2 NURBS曲面

在计算机中，很多曲线和曲面都可以通过样条曲线等参数曲线来描述。其中，B样条（B-Spline）在工业设计中的应用十分广泛[12]。k次B样条曲线的表达式如下：

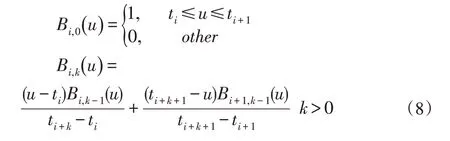
其中ti为节点值构成了样条曲线的节点矢量矩阵。

3D设计中经常包括NURBS（Non-Uniform Ratio⁃nal B-Spline），非均匀有理B样条曲线是一个分段的有理多项式函数，其定义如下：

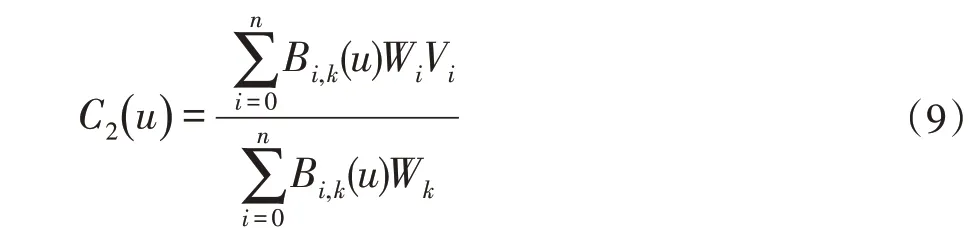
其中k为幂次，ui(i=0,1,…,m)为节点，当幂次=k，控制点数=n+1，节点数=m+1时，可以得到m=n+1。

三维NURBS曲面的定义如下：

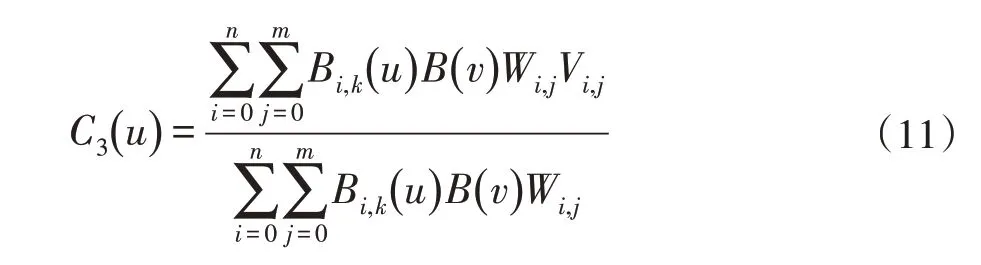
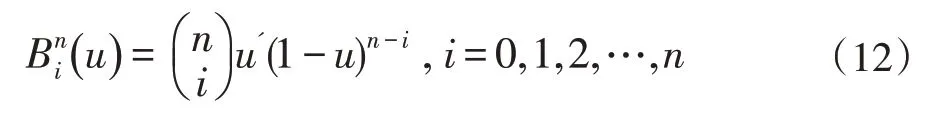
定义样条曲线的求值器P(u)，且u∈[0,1]，表达式如下：

其中Pi表示控制点，如果u的取值范围为，求值器的值为：

对于二维曲面，求值器的表达式为：

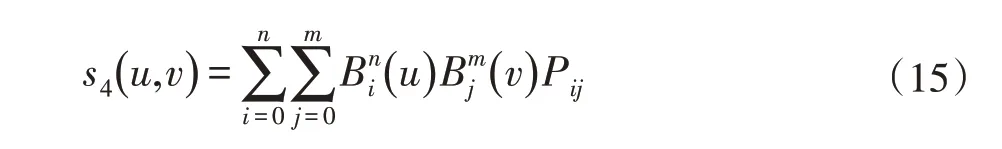
一般来说，实际使用的NURBS曲面和Bezier曲面都少于4次，常用的是3次曲面。B样条曲面和Bezier曲面都可以通过调整控制点来控制曲面的形状，造型能力很强。通过OpenGL实现的NURBS曲面如图4所示：

图4 NURBS曲面

3 纹理映射的实现

纹理映射实现就是将一张纹理图像贴到三维物体表面，就像贴墙纸一样。下面介绍曲面纹理映射的实现过程。

3.1 纹理映射的实现步骤

纹理映射的实现过程主要包括下面的一些步骤：纹理定义、纹理控制、确定映射方式和纹理坐标的确定。

（1）创建纹理：

创建一个纹理对象，并将它和纹理单元进行绑定。或者直接读取已知的纹理图像，然后绑定，一般情况下纹理认为是二维的。

（2）建立映射函数：

映射函数用来表示纹理坐标和三维物体坐标之间的对应关系，有参数表达式的曲面，可以直接利用它们的参数表达式。有时候也需要利用中间曲面，就是建立到中间曲面的映射函数。不同的物体之间的映射函数不一样，需要建立一个顶点之间的映射关系。

（3）设置映射方式：

设置纹理映射的颜色参数，有时可以直接将纹理图像作为颜色映射到曲面上，纹理就好像被粘贴在曲面上；如果想得到比较好的光照和纹理综合效果，把景物曲面的颜色或颜色比例和纹理图像的纹理值结合，通过纹理值来灵活调整；还可以采用一种混合的方式：把曲面原来的颜色和一个固定颜色纹理值进行混合。

（4）激活纹理映射：

先对纹理进行处理：与指定颜色和法向量类似，需要为每一个顶点分配纹理坐标。在最终的绘制之前，需要激活纹理映射。

（5）绘制几何场景：

在进行最后的映射之前，需要了解纹理相对于曲面是怎么排列的，必须指定场景中物体的纹理坐标和几何坐标。经过几何变换之后顶点在屏幕上绘制的位置是由几何坐标决定的，而纹理坐标决定纹理图像中哪个纹理像素值赋值给该顶点。

3.2 实验结果

实验以VC++2013为编程环境，利用OpenGL对纹理映射技术进行研究和验证。通过OpenGL实现了曲面纹理映射，图4展示了把一个带状纹理映射到茶壶表面的效果图；Bezier曲面的纹理映射效果如图5所示：将一个棋盘纹理图像映射到双三次Bezier曲面上。

图5茶壶曲面纹理映射

图6 Bezier曲面上的纹理映射

4 结语

本文通过研究曲面纹理映射算法，对经典的纹理映射算法进行了总结和分析；结合两步法纹理映射技术，研究了自由曲面和参数曲面中的纹理映射算法；并利用OpenGL实现了参数曲面纹理映射算法，以及对相关的曲面纹理映射技术进行了验证。实验结果表明，这些纹理映射算法中可能会产生反走样现象，这个问题还没有很好地解决，还需要深入研究，后续将着重研究如何减少映射过程中的反走样现象，这些研究内容对纹理映射的应用有重要意义。