BDS-2/BDS-3伪距单点定位精度分析

方欣颀,范磊

(1.北京航空航天大学 电子信息工程学院,北京 100191;2. 卫星导航与移动通信融合技术工信部重点实验室,北京 100191)

0 引 言

北斗二号系统(BDS-2)于2012年底开始向亚太地区提供定位、导航和授时(PNT)服务．截至2019年10月,BDS-2已形成由6颗地球静止轨道(GEO)卫星、7颗倾斜地球同步轨道(IGSO)卫星和3颗中圆地球轨道(MEO)卫星组成的星座构型．为了将北斗卫星导航系统(BDS)的服务区域由亚太地区扩展到全球,我国于2015年启动北斗三号全球系统(BDS-3)的组网工作,并在2018年底完成BDS-3基本系统的建设,开始提供全球服务．截至2019年12月,BDS-3在轨正常工作的卫星包括:18颗MEO卫星和2颗IGSO卫星(http://www.csno-tarc.cn/system/constellation),预计到2020年底,BDS-3将完成全部30颗卫星的部署．BDS-3将提供4个基本导航服务公开信号频点B1I(1561.098 MHz)、B3I(1268.520 MHz)、B1C(1575.42 MHz),B2a(1176.45 MHz)[1]．BDS-3卫星选用了稳定度更高的铷钟和氢钟,卫星信号不仅类型更加丰富,信号质量也得到显著提高[2-3]．

伪距单点定位(SPP)定位速度快,使用方便,是在普通用户中应用最广泛的定位方式．国内外学者对SPP进行了大量研究．唐卫明等[4]基于北斗跟踪站实验网的实测数据模拟分析了不同遮挡条件下BDS-2/GPS组合的SPP定位性能．安向东等[5]利用BDS连续观测基准站网的观测数据对比分析了BDS-2和GPS SPP定位性能的差异．杨武召等[6]基于iGMAS的观测数据评估了使用BDS-3各信号进行单频SPP以及使用B1I+B3I组合进行双频SPP时的定位精度．景一帆等[7]发现在经度相差不大的不同测站,BDS-2的相对定位精度存在明显的纬度效应,纬度越高,定位精度越差．周仁宇等[8]在分析北斗系统电离层延迟广播模型性能时,对比了8个不同纬度地区测站分别使用3种不同广播模型进行电离层延迟改正时的SPP定位精度．杨元喜等[9]基于BDS-3试验卫星的实测数据,预测了BDS-3完全建成后不同地区的伪距噪声、多径效应和SPP定位精度水平．Yize Zhang等[10]基于IGS的观测数据对BDS-3 SPP、实时动态载波相位差分技术(RTK)定位精度,位置精度衰减因子(PDOP)、信号空间测距误差(SISRE)进行了评估和分析．Dai Peipei等[11]基于iGMAS的观测数据,比较了群延迟(TGD)改正对于BDS-2、BDS-3 单、双频SPP定位精度的影响,发现TGD改正后SPP定位精度较改正前有了大幅度的提高．

综上,目前国内外对BDS-2/BDS-3组合星座定位精度的研究还比较有限,且尚未有学者使用大量数据对BDS-2/BDS-3全球范围SPP定位精度及其随经纬度分布进行深入研究．因此,在BDS-3基本系统提供服务的背景下,考虑到大部分用户使用的是单频定位终端,本文通过采集37个全球GNSS服务组织(IGS)多模实验跟踪网(MGEX)观测站90天北斗单频(B1I)伪距观测值[12],在全球范围对BDS-2、BDS-3单系统以及BDS-2/BDS-3组合SPP定位精度进行了分析,并评估了BDS-2/BDS-3组合对BDS-2单系统SPP定位精度边缘效应的改善程度．

1 伪距单点定位数学模型

1.1 SPP观测模型

SPP观测方程为

cVtR+cVtSi-(Vion)i-(Vtrop)i+δρi+

(δρmul)i+εi，

(1)

(2)

(3)

(4)

将式(3)表示为矩阵形式得[13]:

(5)

几何精度衰减因子(GDOP)反映了可观测卫星星座空间几何构型,通常用来辅助评估分析用户的定位性能．GDOP的计算方法为

GDOP=

(6)

式中，H为式(5)中确定的系数矩阵,下标表示元素在矩阵中的位置．

1.2 单频用户的设备时延偏差修正

BDS-2和BDS-3均以B3I信号的设备时延为基准设备时延,包含在广播星历播发的钟差参数中[14]．因此,利用B1I频率信号伪距观测值进行用户端定位时,除了式(1)给出的修正项,还需要加以设备延迟偏差的修正,修正方法[15]如下:

TGD1=τB3-τB1，

(7)

ΔtB1=ΔtB3-TGD1.

(8)

式中:τB1和τB3分别为B1频率和B3频率的星载设备时延;TGD1参数可从导航电文中获得;ΔtB3为广播星历播发的以B3频率为基准的卫星钟差．

1.3 基于验后残差的选权迭代算法

观测值粗差、广播星历粗差等,若不加以处理会严重影响用户的定位结果．本文采用基于验后残差的选权迭代方法[16],对观测值的权重进行不断修正,从而尽可能避免观测值粗差或广播星历轨道与钟差粗差对定位的影响．基于验后残差的选权迭代计算流程如图1所示．

图中Ei表示卫星相对用户站的高度角,K是选定的伪距残差经验阈值．该过程基于验后伪距残差υi,在迭代过程中不断重新定权,降低伪距残差大的卫星在计算过程中的权重,并剔除每轮迭代中伪距残差最大且残差值超过经验阈值K的卫星,直至式(5)中ΔX矢量的三个位置分量值小于规定精度对应的阈值ε,以减小粗差对定位结果的影响．

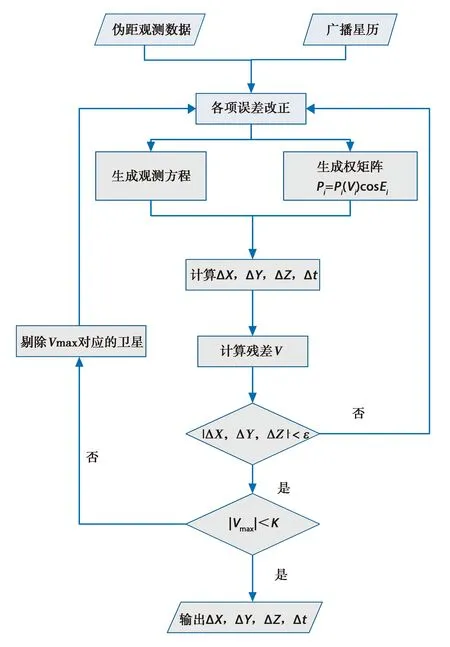
图1 基于验后残差的选权迭代流程图

2 数据采集及处理策略

通过收集2019年4月1日(年积日91)至2019年6月29日(年积日180)37个IGS MGEX站总共90天的实测数据(测站分布如图2所示),分析了BDS-2单系统、BDS-3单系统及BDS-2与BDS-3组合在全球范围的可见卫星数、GDOP和定位精度,并进一步评估了BDS-2与BDS-3组合对BDS-2单系统SPP定位精度及其边缘效应的改善程度．本文数据处理策略由表1给出．其中,电离层延迟修正使用的是北斗Klobuchar 八参数模型,模型参数可直接从导航电文中获得．

表1 数据采集及处理策略总结

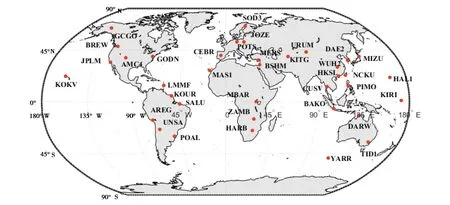
图2 所选37个IGS MGEX站全球分布图

3 实验结果分析

3.1 BDS-2/BDS-3伪距单点定位精度评估

图3示出了各站单天GDOP平均值随平均可见卫星数变化情况．从图中可以看出GDOP与可见卫星数呈明显的相关关系,即可见卫星数越多,GDOP值越小;BDS-3可见卫星数为5～7颗,并且,BDS-2和BDS-3可见卫星数相等的情况下,BDS-3的GDOP明显优于BDS-2,表明了全球系统相对于区域系统具备更好的几何构型;此外从可见卫星数6～12对应的图形可以发现,BDS-2/BDS-3相较于BDS-2 GDOP值有了显著改善,说明BDS-2/BDS-3组合能显著改善BDS-2的空间几何构型．

图3 GDOP随可见卫星数的变化

URUM站(地理坐标87°36′2.4″S,43°48′28.6″E)位于中国的乌鲁木齐市,图4示出的是该站在2019年年积日165的位置偏差和GDOP随时间变化情况．其中,测站位置坐标的“真值”是利用武汉大学开发的PANDA软件进行GPS精密单点定位(PPP)获得的参考值[19]．由于利用IGS事后精密星历计算得到的GPS的PPP的定位精度可达1～2 cm,因此可以作为可靠的比较基准．从图中可以看出,在普通单频定位条件下,一天中BDS-2、BDS-3、BDS-2/BDS-3组合在该站的水平定位精度均优于5 m,垂直定位精度均优于10 m;BDS-3的水平定位精度略优于BDS-2,垂直定位精度明显高于BDS-2;一天中的绝大部分时间,BDS-3的GDOP优于BDS-2,但可用性相比BDS-2仍有一定差距,这主要是因为现阶段BDS-3在轨正常工作的卫星仍然有限,且卫星在全球的分布较为均匀,在亚太地区的可见卫星数低于BDS-2．

图4 URUM站定位误差随时间变化情况

图5所示的是定位结果在E、N、U方向位置偏差的均方根(RMS)．BDS-3在E、N、U方向位置偏差的RMS分别为1.490、2.610、5.238 m,BDS-2分别为3.58、2.65、6.89 m,BDS-2/BDS-3分别为1.45、2.36、4.90 m．BDS-3相对于BDS-2分别改善了58%、1%、24%,BDS-2/BDS-3组合相对于BDS-2分别提升了59%、11%、29%．BDS-2/BDS-3组合相对于BDS-3则提升了3%、10%、6%．由此可见,由于全球布局,BDS-3较BDS-2的定位性能有了明显的提升,并且BDS-2/BDS-3组合相对于BDS-2及 BDS-3单系统均有所提高．

图5 所选37个测站定位误差

3.2 BDS-2/BDS-3伪距单点定位精度随地理经纬度的变化分析

为进一步分析BDS单频SPP定位精度与测站经纬度有关的分布特征．本文计算了每个站BDS-2、BDS-3、BDS-2/BDS-3三种定位模式下在90天时间内单日的定位误差RMS,并将结果分别按测站经度和纬度进行排列,结果如图6所示,其中右侧图中用灰色底色表示BDS-2的服务区域．

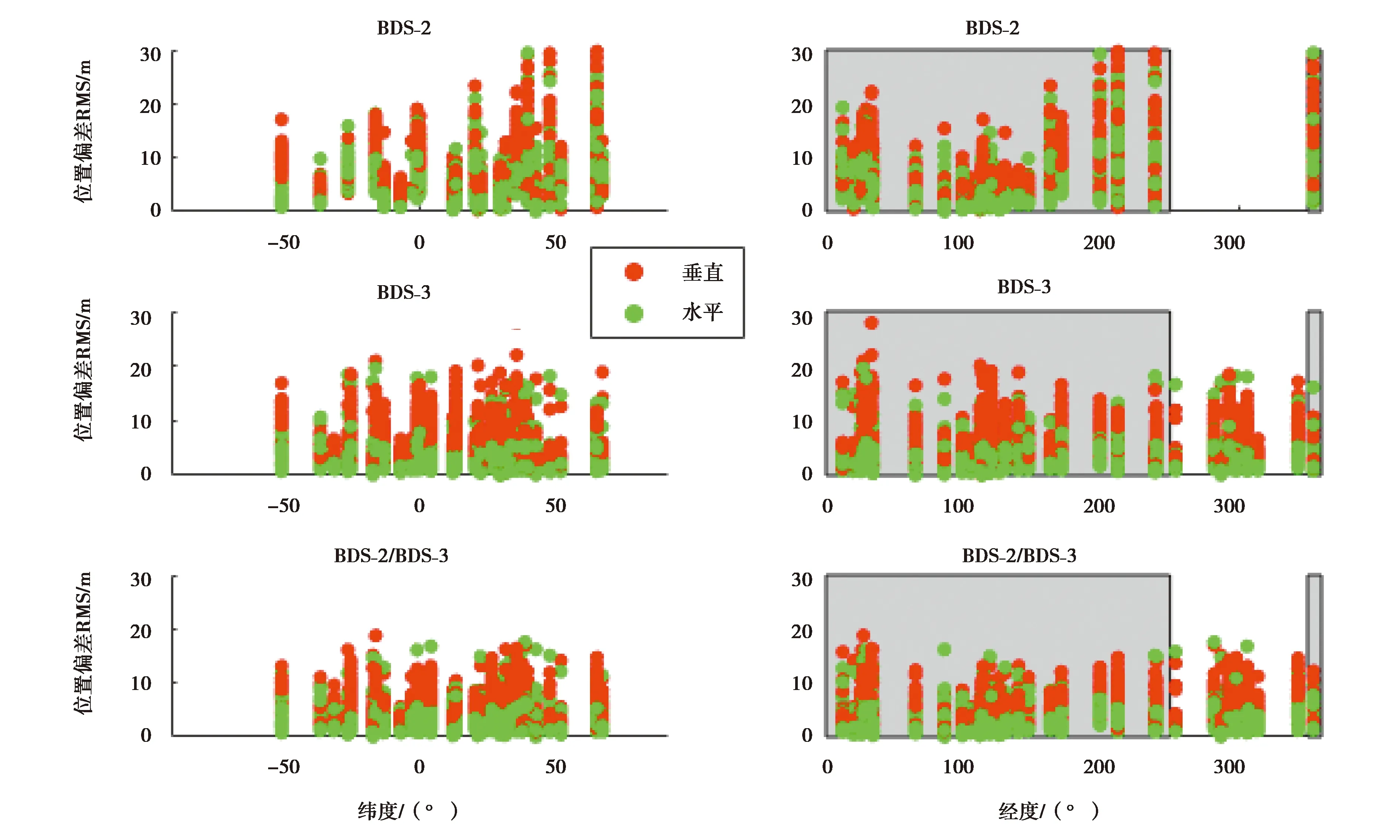
图6 BDS-2、BDS-3、BDS-2/BDS-3定位结果位置偏差RMS随测站经纬度的分布

从左侧图中可以看出,三种不同定位方式的定位精度随测站地理纬度的变化较为平缓,未显现出明显的纬度边缘效应．从右侧图可以看出,BDS-2定位精度随测站经度的变化产生了较大差异,其中在100°E左右(BDS-2服务区域中心地带)的地区定位结果位置偏差RMS最小,靠近服务区域的边界,位置偏差RMS最大．这说明BDS-2定位精度存在明显的经度边缘效应．相较于BDS-2,BDS-3定位精度则不存在类似明显的经度边缘效应．这是因为BDS-3卫星在全球分布较为均匀,可见卫星数与GDOP值在全球不同区域较为稳定,因而定位精度不存在明显的区域分布特性．此外,从图中还可以看出利用BDS-2/BDS-3组合定位不仅明显削弱了BDS-2定位精度存在的经度边缘效应,也进一步提高了BDS-2在亚太地区的定位精度．

4 结束语

本文基于全球多地区长时段的IGS MGEX站观测数据,对BDS-2、BDS-3单系统和BDS-2/BDS-3组合系统在全球范围内的可见卫星数、GDOP和北斗单频伪距单点定位精度进行了比较分析评估．结果表明:

1) BDS-3全球系统相较于BDS-2区域系统在空间构型方面有着明显的优势,在可见卫星数相等时,BDS-3的GDOP值明显低于BDS-2;BDS-2/BDS-3组合系统较BDS-2单系统具有更好的空间几何构型．

2) BDS-3在E、N、U方向位置偏差的RMS分别为1.49、2.61、5.24 m,BDS-2分别为3.58、2.65、6.89 m,BDS-2/BDS-3分别为1.45、2.36、4.90 m．BDS-3相对于BDS-2分别改善了58%、1%、24%,BDS-2/BDS-3组合相对于BDS-2分别提升了59%、11 %、29%．BDS-2/BDS-3组合相对于BDS-3则分别提升了3%、10%、6%．

3) BDS-2的定位精度分布存在着明显的与测站地理经度有关的分布特征．BDS-2和BDS-3组合能明显削弱BDS-2定位精度的经度边缘效应．