加固膨胀土边坡的单排抗滑桩受力性能分析

杜兆萌 肖世国，2

（1.西南交通大学地球科学与环境工程学院，成都 610031；2.西南交通大学高速铁路线路工程教育部重点实验室，成都 610031）

膨胀土边坡中膨胀土在含水率变化时反复膨胀收缩造成边坡整体失稳，给人类工程建筑带来严重损坏。抗滑桩以其良好的抗滑性能在边坡治理工程中得到广泛应用，抗滑桩上承受的滑坡推力是抗滑桩设计中的重要参数。实践中膨胀土边坡稳定性分析大多采用经典的极限平衡方法［1-3］，因此如何在传统的极限平衡法中引入膨胀力是关键。

1975 年，Ito 等［4］从塑性流动理论出发提出了一种抗滑桩受力的计算方法。此后，Ito 等［5］又采用瑞典条分法对其做了改进。1992 年，Reese 等［6］采用简化Bishop法搜索抗滑桩加固后的滑面。1995年，Poulos［7］总结了采用稳定性分析方法计算抗滑桩所受的推力。目前，基于极限平衡理论的严格条分法［8］是工程实践中边坡稳定性分析时推荐采用的重要方法，对于抗滑桩加固的膨胀土边坡，有必要探讨采用包括严格条分法在内的多种方法分析抗滑桩受力。

有鉴于此，本文基于坡体中膨胀力分布模式，将膨胀力引入到抗滑桩加固的边坡稳定性分析中，以建立膨胀土边坡抗滑桩受力计算方法。由于桩间土体对抗滑桩受力也存在影响，分别给出考虑与不考虑桩侧土体作用的滑面处桩体剪力上、下边界值的解。

1 边坡膨胀力作用模型

膨胀土边坡受风化作用和含水率的变化影响，不同深度的膨胀力作用效果不同。坡面表层不受约束且水分变化大，膨胀力的作用规律为从零开始逐渐增大；在浅层受表层与深层两侧约束且水分变化较均匀，膨胀力作用近似不变。实际调查与分析显示，膨胀土边坡多以浅表层滑动为主，滑体厚度一般为2～5 m［9］，膨胀土边坡的大气影响深度为4～6 m［10］。因此，坡体滑动面大多穿过膨胀力影响区。为简化计算，本文采用表层和浅层的膨胀力作用模型为折线型［11］，如图1所示，D和D1分别为表层和浅层厚度，p为膨胀力。

图1 膨胀力作用规律示意

基于Mohr-Coulomb 强度理论，考虑膨胀力作用的土体抗剪强度τf为

式中：c为黏聚力；φ为内摩擦角；σ为不考虑膨胀力作用时的法向压应力。

2 抗滑桩受力分析方法

抗滑桩受荷段受力分析如图2 所示，抗滑桩的截面长度和宽度分别为a0，b0，桩体受荷段作用有前后土体的法向力E1，E2和切向力F1，F2。在桩体受荷段底面有剪力Q，弯矩M和轴力Nz。若完全考虑桩间土体的影响，则受荷段还作用有侧向土压力E0和膨胀力p。为简化分析问题，E0按静止土压力且以三角形分布模式计算，p按图1 膨胀力作用模型计算，即认为膨胀力在边坡表层范围内为线性变化，在浅层及其以内则保持不变。桩间土体产生作用于桩体受荷段侧表面的摩阻力E，其方向与桩上坡体推力方向相同，称为附加推力。E与桩后（平面内）坡体推力一起构成作用于桩体受荷段上的总推力。若完全考虑总推力的作用，则得到的桩体内力即为桩体受荷段底端剪力的上边界值。若完全不考虑桩间土体的影响，相当于传统的桩墙式分析模式，将桩间土体均视为桩体的一部分，则作用于桩体受荷段的推力只有桩后的坡体压力，得到的桩体内力即为桩体受荷段底端剪力的下边界值。此外，在桩体受力分析过程中，对于桩前抗力，以其值不超过桩前土体的被动土压力与剩余抗滑力二者中的小值作为控制条件。同时，不计桩间局部土体沿滑面的阻抗（抗剪）作用，以偏保守分析问题。

图2 抗滑桩受荷段受力示意

据桩体受荷段的静力平衡条件，弯矩M为

式中：h0为桩体受荷段高度；ξ为受荷段净推力（桩后推力减去桩前抗力）作用点距滑面高度与h0的比值，通常可取 1/3-1/2［12］。

由此，根据圆弧滑动条分法，将桩体受荷段底端Q，M和Nz引入到边坡稳定系数计算公式中，并结合桩体受荷段静力平衡条件，即可得到Q与坡体稳定系数K的关系式。其中，完全考虑桩间土体作用时得到Q上边界值，完全不考虑桩间土体作用时得到Q下边界值。

2.1 Fellenius法

在抗滑桩加固的膨胀土边坡内，将圆弧滑面内的潜在滑体竖向分为n条。根据 Fellenius 法［13］，边坡支护后的稳定系数K为作用于滑体抗滑力矩与滑动力矩之比，采用式（1）所示的土体抗剪强度，完全考虑桩间土体作用与完全不考虑桩间土体作用，经推导可得式（3）、式（4）所示的稳定系数表达式。当已知K时，可反算出抗滑桩受荷段底端剪力Q的上、下边界值解。Q的上边界值控制方程为

Q的下边界值控制方程为

式中：Wi为第i个土条的自重；αi为第i个土条滑面倾角；α为设桩位置处的滑面倾角；pi为第i个土条滑面上的膨胀力；li为第i个土条滑面处长度；轴力Nz由桩体受荷段静力平衡条件确定，即为Nz=Wz（根据Fellenius法假定两侧条间力是一对平衡力），Wz为抗滑桩受荷段的自重；R为圆弧滑面的半径。

2.2 简化Bishop法

简化Bishop条分法［14］计算边坡稳定系数K时忽略了土条间切向力的作用，并假定潜在圆弧滑面上各点抗剪强度与相应方向的剪应力之比都相等。经推导可得求解桩体剪力Q的上边界值控制方程为

经推导可得求解桩体剪力Q的下边界值控制方程为

式中：mαi为计算系数，mαi= cosαi+ tanφisinαi/K。

2.3 Morgenstern-Price法

Morgenstern-Price 法［15］假定相邻土条间的法向力Ei和切向力Fi中存在对水平方向坐标x的函数关系，即Fi=λf(x)Ei，其中λ为任意常数，f（x）为已知函数。

为简化计算，假定第i个土条两侧的法向力Ei中包含条间膨胀力pi，且Ei和Ei+1在第i个土条两侧的作用点距离滑动面的高度分别为yi和yi+1。将潜在滑体分为n个土条，并将抗滑桩加入膨胀土边坡中，K，Wi，pi，Wz和E已知，未知量为Q，λ，Ei，Ei+1，Fi，Fi+1，yi，yi+1，Ni'，Ti，E1，E2，F1，F2，y1，y2和Nz共计8n+9个未知量。其中，Ni'为第i个土条滑面上的法向力；Ti为第i个土条滑面上的切向反力。

每个土条的静力平衡方程，共3n个，分别为

抗滑桩的静力平衡方程，共3个，分别为

其中

式中：b0为抗滑桩截面宽度；m为内摩擦系数；K0为静止土压力系数；γ为土的重度。

在条间界面上由力的连续性，可得2n个方程，分别为

滑动面的抗剪强度τfi方程，共n个方程，即

Ei和Fi之间存在函数关系，共2（n+1）个方程，分别为

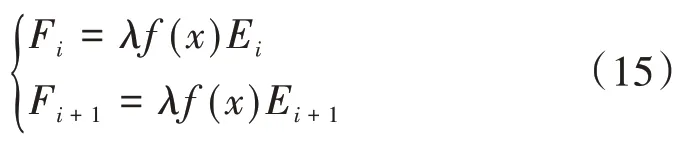
当滑体上无其他外力作用时，第1 个和第n个土条必须满足以下关系

根据式（7）—式（16）可得8n+9 个独立方程，联立求解即得到任意安全系数K情况下抗滑桩剪力Q的上边界值。若不考虑桩间土体的影响，即在上述求解过程中令E=0，即可得出桩身剪力Q的下边界值。

2.4 Spencer法

Spencer 法［16］假定相邻土条间的法向力和切向力之比为固定常数，Fi/Ei=Fi+1/Ei+1= tanθ，θ为任意常数。此方法是Morgenstern-Price 法中条间力函数f（x）为常数时的一种特殊情况，因此采用Spencer 法计算抗滑桩剪力Q的上、下边界值过程同Morgenstern-Price法。

根据前述方法，确定出抗滑桩受荷段底端的内力后，即可按照传统的弹性桩或刚性桩法［17］计算桩体嵌固段的内力与位移。

3 加桩边坡最危险滑面搜索方法

膨胀土属于黏性土，可将其滑面视为圆弧形曲面。图3 为加桩边坡最危险滑面搜索示意图。首先，应用Fellenius 法得出滑面圆心位置，此圆心作为起始圆心O1，计算出相应的抗滑桩剪力Q1。其次，确定最危险滑面所对应圆心位置的搜索步长，以步长作为网格单元的边长。然后，依次将O1周围的4 个网格点O2，O3，O4和O5作为圆心，计算对应的抗滑桩剪力Q2，Q3，Q4和Q5。将五者中剪力最大者对应的圆心O作为下一次搜索的起始圆心O1，如此反复搜索，直到周围4个网格点所对应的剪力值均小于中心点所对应的剪力值，所得到的滑面就是加桩边坡最危险滑面。

图3 加桩边坡最危险滑面搜索示意

4 实例分析

云桂铁路DK221+800［18］工点路堑边坡横断面如图4 所示，线路的右侧为膨胀土边坡。边坡几何尺寸和土体现场试验得到的相关参数见表1，边坡表层厚度取1 m。原位试验测得天然含水率为14.18%，饱和含水率为15.6%，降雨时深度135 cm 处膨胀力最大值为20 kPa，抗滑桩的设计参数见表2。

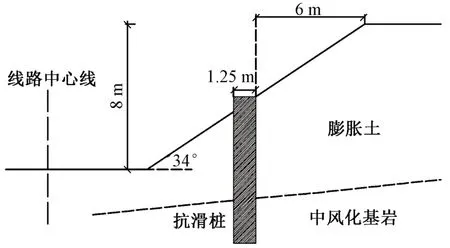
图4 实例边坡横断面示意

表1 实例边坡物理力学参数

表2 抗滑桩设计参数

根据前述分析方法，计算得到单排抗滑桩将边坡加固到K=1.5时，不同膨胀力时剪力Q上、下边界值计算结果见表3、表4。

表3 实例Q的上边界值计算结果

表4 实例Q的下边界值计算结果

由表3、表4 可知：考虑膨胀力作用时，Fellenius法、简化 Bishop 法、Morgenstern-Price 法（取f（x）=sin（πx/L））及Spencer 法的桩体剪力Q上边界值分别为957.36，942.69，817.86，814.99 kN。若以Morgenstern-Price 法为基准，其余3 种方法相对偏差分别为17%，15%，0.4%。同时，这4种极限平衡方法的Q下边界值分别为839.32，833.54，710.15，708.33 kN。其余3种方法相对于Morgenstern-Price 法的偏差分别为18%，17%，0.3%。对比这4 种方法的剪力计算结果，Fellenius 法相对最大，Spencer 法相对最小。同属于简化条分法的Fellenius法和简化Bishop法计算结果较为接近；而同属于严格条分法的Morgenstern-Price 法和Spencer法计算结果则基本一致，说明计算过程中条间力函数f（x）的选取对剪力Q的计算结果影响很小。同时，若不考虑膨胀力，桩体剪力约降低80%～90%，偏于不安全。

前述4 种方法计算得到的边坡最危险滑面，距坡面的法向深度约为3～6 m。以Morgenstern-Price 法为例（图5），最危险滑面距坡面的法向深度为3.09～4.11 m。由我国部分膨胀土地区膨胀土湿度波动多年实测曲线［19］可见，膨胀土地层一般在深度0～6 m内含水率变化，而计算得到的该实例边坡最危险滑面位置也在此范围内，二者吻合良好。

图5 Morgenstern-Price法计算滑面位置

5 膨胀力影响分析

为进一步探讨膨胀力作用的影响，本文给出考虑和不考虑膨胀力时桩体剪力与边坡稳定性特征。以坡高6 m、坡角33.7°、黏聚力5 kPa、内摩擦角14°、重度19.6 kN/m3、桩间距为6 m、桩体截面尺寸为0.4 m×0.4 m、设计安全系数K=1.35 的抗滑桩加固膨胀土边坡为例进行计算。在不同膨胀力作用下，采用前述4 种方法得到的边坡最危险滑面及Q的上、下边界值，上边界值见图6，下边界值规律与其一致。可见，随着膨胀力增大，抗滑桩剪力随之增大，4 种方法中Fellenius 法计算的结果偏大，而其余3 种方法计算结果接近。同时，这4 种方法得到的滑面位置变化趋势相同，滑面深度随膨胀力的增大而增大。

图6 膨胀力对抗滑桩剪力上边界值影响

6 结论

基于膨胀土边坡膨胀力随深度变化模式及4类经典的极限平衡条分法，给出了考虑与不考虑桩间土体作用的2 种情况下，加固膨胀土边坡的抗滑桩计算方法，并讨论了膨胀力的大小对抗滑桩剪力的影响，主要得到如下结论：

1）在不计桩间局部土体沿滑面阻抗作用的前提下，当完全考虑桩间土对抗滑桩的作用时，其对桩身产生附加推力，由此得到的抗滑桩内力是桩身内力的上边界值；而完全不考虑桩间土对抗滑桩的作用时，得到的是桩身内力下边界值。

2）将膨胀力引入抗滑桩加固膨胀土边坡稳定性分析的极限平衡条分法中，对于Fellenius 法、简化Bishop 法、Morgenstern-Price 法和 Spencer 法，给出了考虑膨胀力影响的加桩边坡的抗滑桩受力分析方法及计算公式。

3）采用Fellenius 法计算得到的抗滑桩剪力，较简化 Bishop 法、Morgenstern-Price 法和 Spencer 法的计算结果偏大，最大偏差约20%，相对偏于保守。抗滑桩加固膨胀土边坡的桩体剪力和滑面深度随膨胀力的增大而逐渐增大。