平板热管散热器传热特性研究及结构优化
高天琦 梁文清* 任海刚
1 东南大学能源与环境学院
2 中国船舶工业系统工程研究院
0 引言
随着现代科学技术日新月异的高速发展,电子器件高频、高速及集成电路的密集和小型化,单位容积电子器件的发热量迅速增大。而随着温度的增加,电子元器件的失效率呈指数增长。当超出元件的工作温度范围时,其性能将显著下降,不能稳定工作,严重影响系统运行的可靠性。因此,电子技术的发展需要良好的散热手段来保证。平板热管具有质量轻,良好的启动性,均温性和超强的导热性的优势,成为目前电子元件散热方面的热点研究方向。
国内外一些专家学者已经对平板热管传热特性做出了相关理论和实验研究。如宣益民等[1]对带烧结毛细芯的平板热管并进行了实验研究。得到了不同输入功率、烧结毛细多孔层厚度、工质充装量下热管的瞬态传热性能及稳态工作时的表面等温特性。Koito 等[2]对具有丝网毛细结构的平板热管进行了数值模拟研究。通过对连续性,能量和动量方程进行求解,给出了平板热管内部的速度,压力和温度场分布。Yasushi Koito 等[3]对于具有真空腔均热板内的热流体现象进行了数值分析,计算了工质循环所需要的毛细管压头和蒸汽腔内的温降。而目前对于采用平板热管散热器冷却电子元件时的传热特性分析及结构参数优化研究较少,因此本文主要通过建立平板热管散热器热阻模型,分析不同结构参数以及相关外部条件如热源尺寸及空气流速对于整体传热性能的影响,并进行优化分析,对于实际工程有一定指导意义。
1 传热模型
1.1 物理模型
本研究中的散热器结构如图1 所示,下部平板热管分为外部热管壁和其内部的吸液芯及蒸汽腔结构,图中箭头指示了热管内部工质流动方向。平板热管上部插有矩形翅片。由于铝热导率较高,单价低,质量轻,因此一般作于平板热管的管壁以及金属翅片的材料。热源紧贴于平板热管底面,通过热管热传导与相变介质的快速热传递性质,可将发热物体的热量迅速扩散开来,并通过翅片扩大散热面积,与空气进行对流换热,起到为发热源降温并增强底面均温性的效果。

图1 平板热管散热器结构示意图
1.2 模型假设
为便于对平板热管散热器进行结构优化及传热数值模拟,做出如下假设:1)系统在稳态工况下运行。2)发热源与散热器以及平板热管和铝制翅片之间良好接触,无接触热阻。3)利用均匀风源代替风机模型,空气仅从翅片间吹过,并且假定空气流速一定。4)忽略散热器与外界环境之间的辐射作用。5)除与热源接触部分,散热器底面以及顶面绝热。6)平板热管冷凝段多孔芯空隙为液膜全部占据,而热管蒸发段多孔芯体中充满液体,汽化与液化均仅在芯层表面上进行[4]。7)吸液芯内部材料均匀分布并且各向同性(孔隙率与渗透率为常数)。
1.3 模型描述
图2 为系统热阻网络图,其中,Tre与TO分别表示热源最高温度与环境温度,各热阻所代表的含义如下:R0为热源与散热器之间接触热阻,根据模型假设可忽略,Rave为平板热管厚度方向上的平均热阻,Rsp为平板热管的扩散热阻,Rh为翅片与空气对流传热热阻,因此有:

式中:Rtotal是散热器总热阻。

图2 系统热阻网络图
结合热管工作原理,探讨热管内部平均热阻Rave的构成如图3 所示,热管两端分别为蒸发端及冷凝端,蒸发段受热输入热量,冷凝端放热。首先通过管壁导热,产生蒸发段管壁导热热阻Res。蒸发段吸液芯内的工作液体受热蒸发,产生蒸发段吸液芯热阻Rew,并在芯层表面气化产生蒸发段气液相变热阻Rei。蒸汽在蒸汽腔内部流动,产生微小温降,伴随蒸汽流动热阻Rv。蒸汽在冷凝端凝结,放出潜热,并通过吸液芯结构返回蒸发端,相应产生冷凝段气液相变热阻Rci,冷凝段吸液芯热阻Rcw,冷凝段管壁导热热阻Rcs。并且在热管侧壁还存在管壁导热热阻Rs与吸液芯热阻Rw。这里假定热管各处壁厚ep与吸液芯厚度ew均匀,并且有:
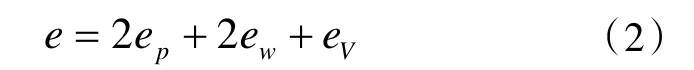
式中:eV与e 分别为蒸汽腔厚度与平板热管总厚度。
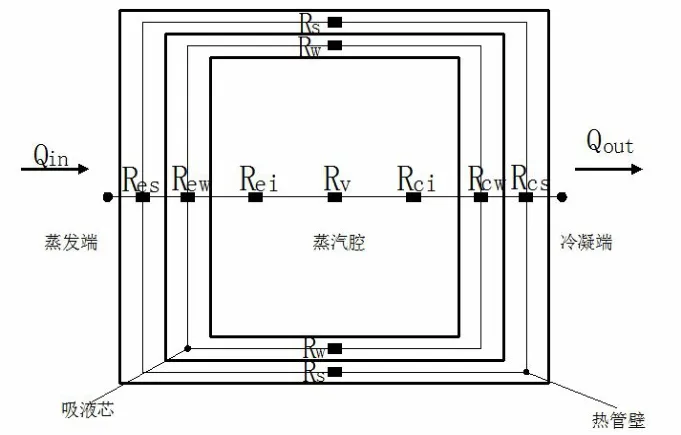
图3 平板热管内部平均热阻构成示意图
热管内部平均热阻Rave计算如下:
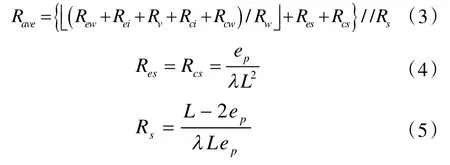
式中:λ 与L 分别为铝热导率和平板热管底边长,这里假设底面为正方形。
热管吸液芯内部原本为液体对流换热和多孔芯固体骨架导热的复合,为便于进行热阻分析,可将此问题折合成导热问题来解,其中的导热系数用当量导热率来替代[5]。量热导率与吸液芯热阻计算公式如下:
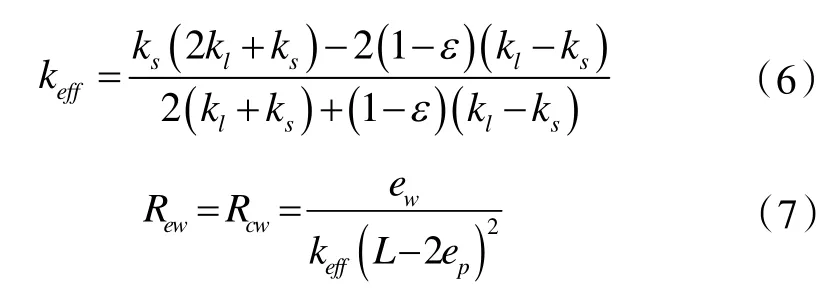
式中:ε 为吸液芯的孔隙度kl与ks分别为液体和多孔芯骨架热导率。
蒸发段气液相变热阻Rei和冷凝段气液相变热阻Rci的计算如下式:

式中:R 代表气体常数T 为蒸汽温度,L 为汽化潜热,PV为蒸汽压力。
蒸汽流动热阻RV计算如下式:

式中:λV为腔内蒸汽导热系数;TV腔内蒸汽温度;eV单位是mm[6]。
平板热管的扩散热阻Rsp计算[7]如下:
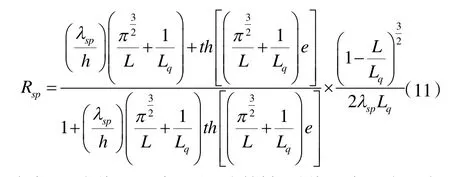
式中:Lq为热源尺寸,这里同样假设热源表面为正方形;h 为对流换热系数;λsp为平板热管平均热导率,可通过热管平均热阻进行计算。

对于翅片对流换热热阻的计算如下:

式中:h 为空气侧对流换热系数;A0为外表面面积;η0为肋壁效率。
为增强翅片对流换热强度,拟将翅片沿平行于平板热管长边方向布置。相关结构参数计算如下:

式中:H 与Hc分别为翅片的高度与修正高度,δ 为翅片厚度,n 为翅片的个数,A1与A2分别为未装肋部分的面积和肋片面积。
对于肋壁效率的计算如下:
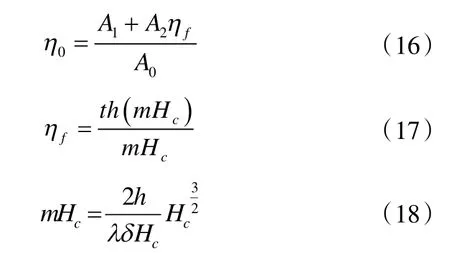
式中:ηf为肋片效率[8]。
2 传热特性分析及结构优化
2.1 平板热管传热特性研究
这里假定所处环境温度为20 ℃,空气流速恒定为10 m/s,平板热管底面L=0.1 m。根据热管运行温度区间以及热管管壁,吸液芯和工质之间的相容性原则,这里的热管吸液芯采用铜粉烧结粉末材质,工质采用丙酮[9]。通过热管管壁强度校核,求出满足要求的最小热管壁厚ep如下:

式中:K 为结构特征参数,取0.31;P 为管内压力;σ 为许用应力。
经计算,本工程ep≥1.52 mm,因此可取壁厚为2 mm。并取ew=1 mm,探究热源尺寸以及蒸汽腔厚度对于传热性能的影响。
由图4 可看出,随着热源尺寸的不断扩大,平板热管内部平均热阻保持不变,扩散热阻不断减小,而热管总热阻也随之不断减小。这是由于热源尺寸的改变不影响热管结构参数,因此平均热阻Rave不会发生变化。而扩散热阻产生于热传导过程中热导体传热面积的变化处,与热源同散热器得接触面积有关,当热源尺寸远小于散热器底面积时,会加剧径向温度不均匀性,而当热源尺寸较大甚至接近散热器底面积时,扩散热阻Rsp会逐渐减小直到径向温差消失,仅在轴向存在温差。而由图5 可看出,随着蒸汽腔厚度不断增加,平均热阻略有上升,扩散热阻不断下降。由于扩散热阻下降幅度更大导致总热阻不断下降,但是下降趋势不断变缓。这是由于蒸汽腔厚度的增加,蒸汽流动热阻Rv会增加,并且管壁导热热阻Rs与吸液芯热阻Rw均随之增加,但由于Rv在10-7量级,而Rs和Rw在与其他热阻并联的基础上,值远大于其他热阻,故致使平均热阻Rave上升幅度较小。蒸汽腔厚度增加,平板热管厚度增加,扩散热阻Rsp随之下降明显,这就是采用蒸汽腔平板热管的优势所在。
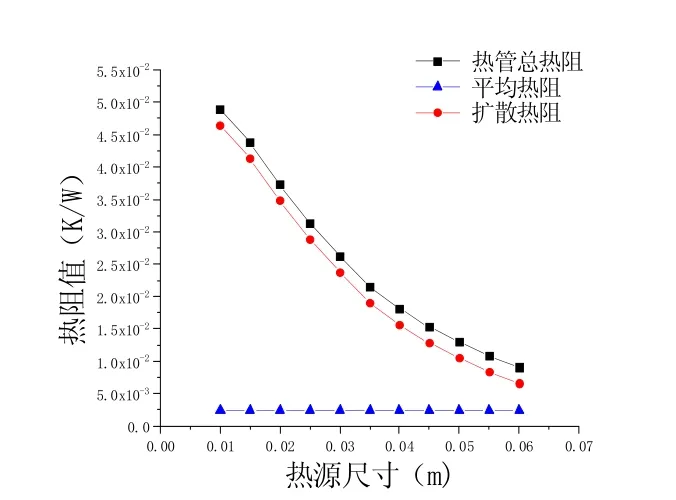
图4 平板热管热阻随热源尺寸变化规律

图5 平板热管热阻随蒸汽腔厚度变化规律
由两图中均可看出,在热源尺寸或蒸汽腔厚度较小时,扩散热阻Rsp在10-2量级,远大于平均热阻Rave的10-3量级,并且总热阻较大,因此在设计时,应综合考虑其对于热阻的影响,选用合适的结构参数。
2.2 翅片传热特性研究及结构优化
假定散热器底面长a=250 mm,宽b=186 mm。同时考虑到散热器的制造和强度因素,一般翅片尺寸的范围是:厚度1~3 mm,间距1~10 mm,高度25~60 mm。而在外部环境条件(空气温度与风速)与散热器底面积不变的情况下,对流换热系数h 不变。能够表征翅片对流换热热阻高低的参数为有效换热面积A0η0,并关注耗材量即翅片总体积V,计算如下:

因此,这里根据不同的翅片高度H,厚度δ 与间距β,计算相应的有效换热系数A0η0与翅片总体积V 如下,因自变量有三个,为方便进行分析,可固定其中一变量的值,这里分别固定H=0.06 m 以及β=3 mm,研究有效换热面积A0η0与翅片总体积V 随其他两变量之间的变化情况。

图6 H=0.06 m 时,A0η0的变化曲线

图7 β=3 mm 时,A0η0的变化曲线

图8 H=0.06 m 时,V 的变化曲线

图9 β=3 mm 时,V 的变化曲线
如图6 所示,从任意一条曲线的变化趋势可看出,在翅片高度H 以及翅片间距β 不变时,有效换热面积A0η0随翅片厚度δ 的增加而减小,这是由于增加翅片厚度会使得翅片个数减小,外表面面积相应减小,虽然肋壁效率能够有所提升,但是其增加程度不如翅片外表面面积减小的程度,故有效换热面积随之下降。从不同曲线之间的变化趋势可看出,有效换热系数A0η0同样随翅片间距β 的增加而减小,这是因为加翅片间距,外表面面积减小,而翅片厚度不变,肋壁效率变化不大,使有效换热面积随之下降。从图7 的不同曲线之间的变化趋势可看出,在翅片厚度δ 以及间距β 不变时,有效换热面积A0η0随翅片高度H 的下降而下降,这是因为肋壁效率增加的程度不如外表面面积减小的程度。图8 与9 反映了翅片体积V 与翅片高度H,厚度δ 成正相关,与翅片间距β 成负相关。
综合上述四图所表现的变化规律,当耗用相同翅片体积时,存在传热量最大的一种翅片结构,即为翅片的最佳尺寸[10],需通过优化计算得出此最优翅片结构参数。翅片结构优化计算过程如图10 所示。
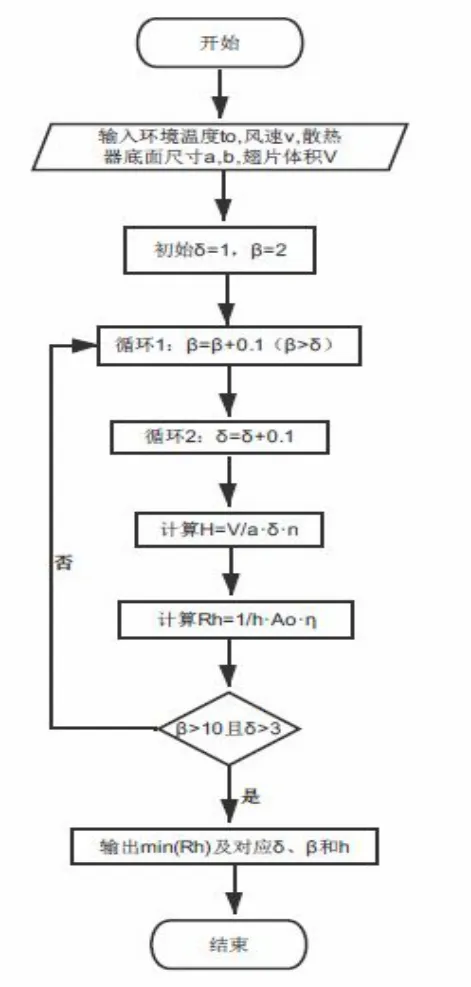
图10 翅片结构优化计算程序框图
例如当环境温度t0=20 ℃,风速v=10 m/s,散热器底面尺寸a=250 mm,b=186 mm。根据不同的翅片体积,计算最优结构如表1:

表1 翅片结构优化计算结果
从表中可看出,当翅片体积较小时,最佳结构的翅片高度较小,而翅片体积较大时,最佳结构的翅片高度较大,而受制于翅片高度的最大值,对流换热热阻随着翅片体积的增大而先变小后变大,若无翅片耗材要求时,在确定散热器地面尺寸的情况下,存在一最佳翅片体积使得对流换热热阻最小。因此在设计时,应结合实际工程,进行结构优化计算,使得散热器散热效果达到最佳。
3 传热数值模拟分析
根据上述优化计算,选定在散热器底面长a=250 mm,宽b=186 mm的情况下散热器的最佳结构尺寸如下:翅片高度H=60 mm,翅片厚度δ=1 mm,间距β=2 mm,平板热管厚度L=20 mm。环境温度为20 ℃,空气流速恒定为10 m/s,热源底面积为126 mm×164 mm 发热功率700 W。通过传热数值模拟对比传统铝制翅片散热器,反映其传热性能的提升程度。并比对平板热管散热器热阻模型计算结果,探究在不同风速下总热阻Rtotal变化情况。
根据模型假设条件,将平板热管内部划分为三个区域:热管壁,吸液芯和蒸汽腔,分别计算当量热导率或热阻。比较平板热管散热器与铝制翅片散热器在均温性和总传热温差的差异。

图11 平板热管散热器表面温度分布
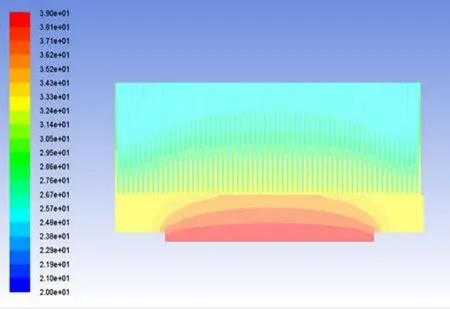
图12 铝制基板散热器表面温度分布
如图11 与图12 所示,平板热管散热器总传热温差为15.9 ℃,而铝制基板散热器总传热温差为19 ℃,在热流密度保持一致的前提下,平板热管散热器的传热效果优于铝制基板散热器。平板热管均温性较强,在水平方向边缘处仍有一定温降,这是由于管壳导热系数远低于热管内部蒸汽腔当量导热系数所致。
如图13 所示,反映了随风速的增加,散热器总阻值不断下降,传热性能提升,下降趋势不断变缓,这是由于在热源及散热器结构参数不变的情况下,平板热管平均热阻Rave,及扩散热阻Rsp两部分均不发生变化,而翅片对流传热热阻Rh会随之下降,因此总热阻Rtotal下降趋势减小。并且此图还反映了采用两种方式进行热阻计算的偏差较小,误差比例在5%之内,因此采用热阻计算简单快捷,结果也较为准确,对于工程计算有一定指导意义。

图13 热阻随风速变化曲线
4 结论
本文建立热阻网络,分析平板热管散热器传热特性影响因素诸如翅片间距,厚度与高度,平板热管蒸汽腔厚度,热源尺寸以及风速并提出了相关优化建议。主要得到以下结论:
1)热源尺寸与蒸汽腔厚度主要影响热管热阻:随着热源尺寸的不断扩大,平板热管内部平均热阻保持不变,扩散热阻不断减小,而热管总热阻也随之不断减小。随着蒸汽腔厚度不断增加,平均热阻略有上升,扩散热阻不断下降,但是下降趋势不断变缓。因此在设计时,应综合考虑其对于热阻的影响,选用合适的结构参数。
2)翅片间距,厚度与高度主要影响翅片对流换热热阻,其中对流换热热阻与翅片厚度及间距正相关,与翅片高度负相关。当耗用相同翅片体积时,存在传热量最大的一种翅片结构,即为翅片的最佳尺寸,并进行了优化程序设计及计算。
3)随风速的增加,散热器总阻值不断下降,传热性能提升,并且通过与CFD 传热数值计算比对,验证了本文的热阻计算法具有一定的准确性,可被工程广泛应用。

