风机盘管实际运行状态下换热性能特征研究

李震宇 刘兆辉 谭洪卫，3*

1 同济大学机械与能源工程学院

2 同济大学绿色建筑及新能源研究中心

3 同济大学联合国环境规划署-环境与可持续发展学院

0 引言

作为半集中式空调系统末端形式中的一种，风机盘管的换热性能受很多因素影响，包括冷水进口温度、冷水流速，空气迎面流速以及自身物理参数等。同时，由于半集中式空调系统在实际运行中往往长时间处于部分负荷状态，风机盘管在实际运行中的状态相比额定工况下往往存在一定偏差[1-2]。大量学者围绕风机盘管换热模型的建立展开研究。具体来说，可以通过基于基础换热过程以及物理模型建立理论动态换热模型来实现[3-4]。但这类复杂模型往往由于输入参数较多，计算成本较高。也有部分模型采用半经验公式对换热过程进行简化，结合盘管自身性能参数的回归模型最终得到换热模型。Rabeh 等人[5]将盘管的换热过程简化为包含三个回归参数的半经验模型，但在计算过程中仍需要确定动态黏度，普朗特数和雷诺数等参数。Wang 等人[6]同样基于能量平衡方程对换热过程进行半经验化，但计算中对盘管进行了全干或全湿工况的假设。另外，盘管的换热量计算的简化方法还包括干湿工况转化法[4，7-8]、焓差法[9-10]等。

然而，这些研究中往往基于某一固定工况或几种假定工况来探究不同因素对风机盘管换热性能（如制冷量）的影响程度。在风机盘管实际运行中，这假定工况下的风机盘管换热性能并不能代表其实际运行状态下换热能力。笔者在建立基于热交换效率的风机盘管换热模型的基础上，以上海地区某一居住建筑为例，借助实测数据从宏观角度对风机盘管的换热进行统计学分析，用以研究风机盘管在长时间实际运行中潜在的分布性规律，同时也对风机盘管换热性能优化潜力进行探究。

1 案例概况

本文研究对象为位于上海地区的某独栋别墅，采用地源热泵空调系统，末端设备采用新晃SGCR-200型风机盘管，额定参数如表1（额定制冷工况为进口空气干球温度27 ℃，湿球温度19.5 ℃，进水温度7 ℃）。

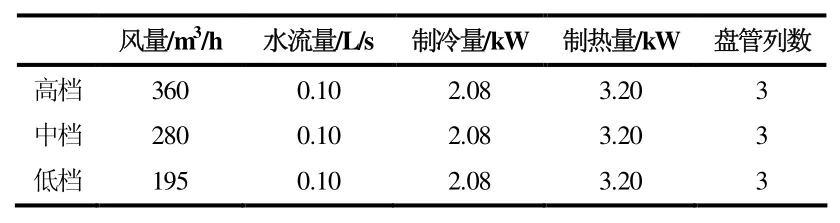
表1 SGCR-200 型风机盘管性能参数

2 室内温湿度分布分析

对供冷季期间共31 天（时间间隔为1 h）室内温湿度情况进行统计分析，获得室内温湿度情况频率分布，如图1、图2：

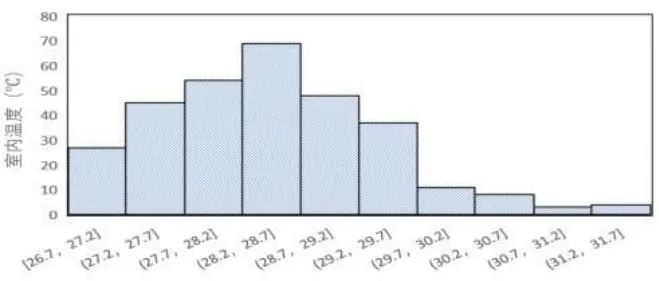
图1 室内温度频率分布图

图2 室内空气含湿量频率分布图

可以发现，在实际运行状态中室内平均温度为28.5 ℃，在94.8%的运行时间内室内温度（即风机盘管进口温度）高于27 ℃（额定工况）。室内空气平均含湿量为13.3 g/kg，在95.4%的运行时间内风机盘管进口空气含湿量高于11.1 g/kg（额定工况）。

3 风机盘管换热模型

3.1 模型建立

由于难以直接测得较为精准的盘管实际全热量、显热量、潜热量，本文建立了基于热交换效率的的盘管换热模型。先假设出风干球温度t2，在给定盘管水流量与风量的情况下可以借助风机盘管通用热交换效率E’得到出风湿球温度ts2，进而得到出风焓值h2等其状态参数。然后，求出热湿过程的析湿系数ξ，借助经验公式得到传热系数与传热面积之积K·F。接着，计算水的当量数γ 与传热单元数Ntu，借助全热交换效率Eg可以得到新的出风干球温度t2’。紧接着比较t2与t2’之差是否在误差δ 之内，否则重新假设出风干球温度t2。最后，根据进出风参数可以计算盘管的显热量、潜热量。具体计算流程如图3：

图3 风机盘管计算模型

3.2 模型验证

借助上文提到的模型，可借助进风口参数以及供水温度推导出回水温度，同时借助实际测出的回水温度，可对模型准确性进行验证。借助厂家样本参数对传热系数的拟合结果如下：

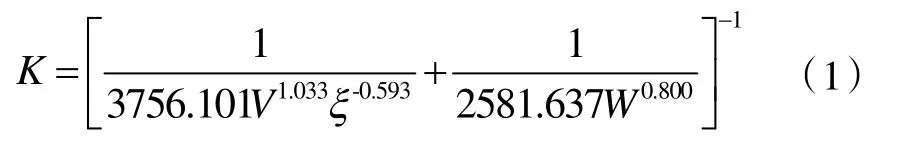
风机盘管模型计算的回水温度值与实际回水温度值的比较如图4，均方根误差（RMSE）为0.597，平均误差率为2.89%。由见，该模型具有较高的计算精度。

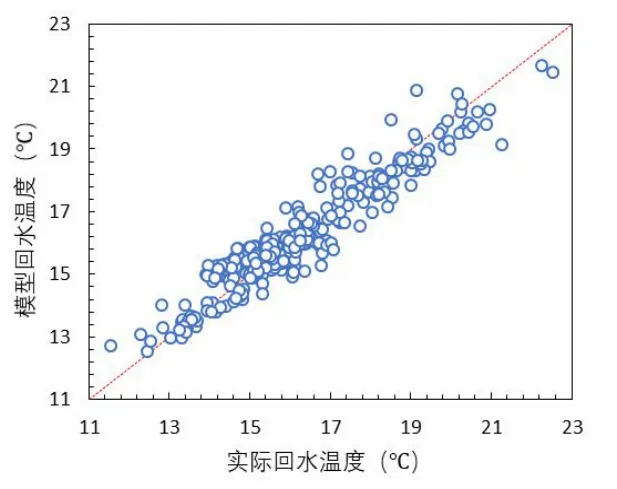
图4 基于回水温度的模型准确性验证

4 实际换热性能分析

4.1 实际工况与额定工况对比

借助模型计算实际工况下风机盘管的换热性能，并与厂家提供的额定工况性能进行比较，如图5（实际工况定义为风机盘管进口处空气干球温度28.5 ℃，含湿量13.3 g/kg，即室内实际状态的平均值）。

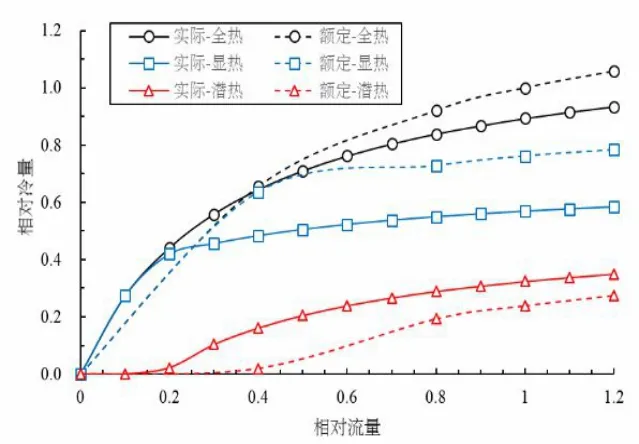
图5 盘管相对冷量-流相对量关系图

可以发现，随着盘管内相对流量提高，盘管换热的显热量与全热量下降均更加明显，在相对流量为1的工况下，实际显热量为额定工况的90%，全热量为额定工况的75%。而对于除湿能力而言，实际状态下潜热量高于额定工况，是由于实际工况下入风口空气含湿量较高所造成的。相对流量为1 时，实际工况下显热量相比额定工况提升了36%。

4.2 实际换热性能频率分布

借助模型对实际运行期间盘管换热性能进行逐时计算，并对全热量，显热量以及潜热量进行分布统计，如图6、图7、图8。

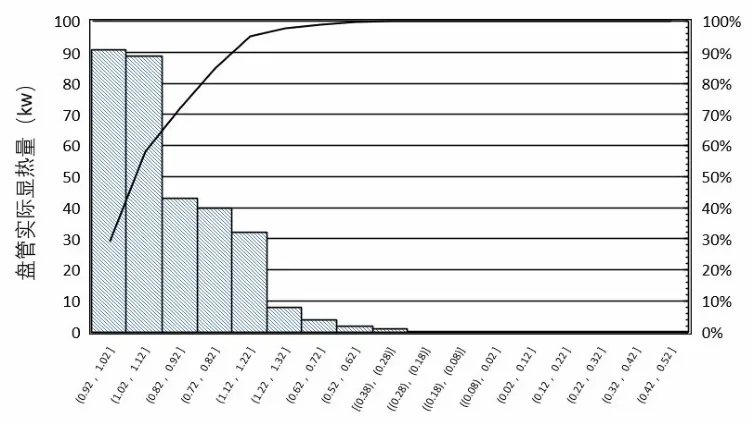
图6 显热量频率分布图

分析实际运行状态下盘管平均全热量1.26 kW，相比盘管额定全热值（1.85 kW）下降39.5%。盘管平均显热量0.98 kW，相比额定工况显热值（1.58 kW）下降37.9%。盘管平均潜热量0.28 kW，相比额定工况潜热值（0.50 kW）下降44.3%。

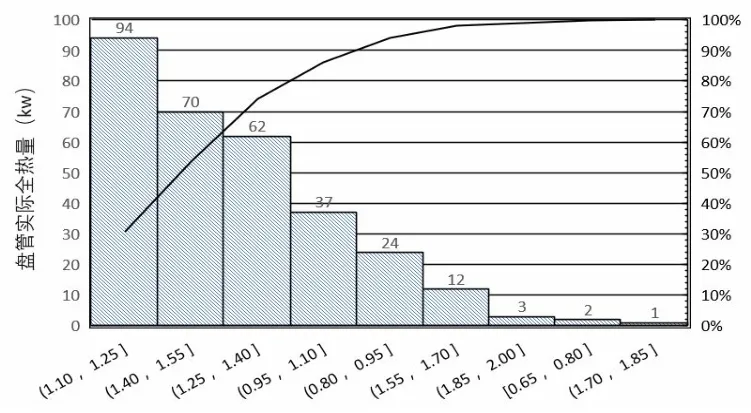
图7 全热量频率分布图

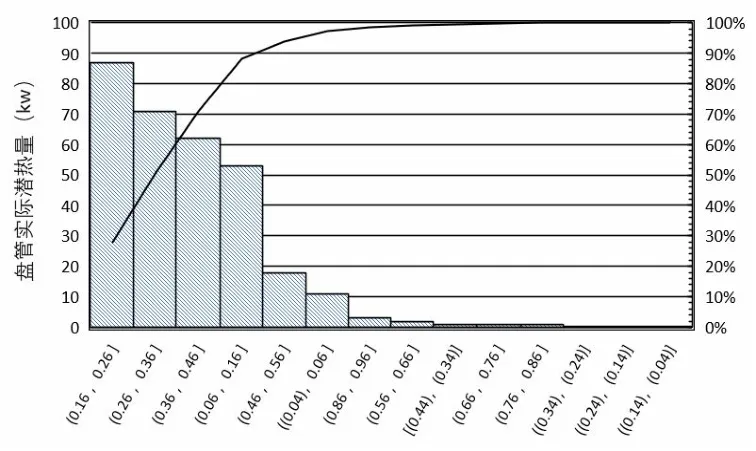
图8 潜热量频率分布图

4.3 换热性能分布正态性分析

本文采用柯尔莫哥洛夫检验法对风机盘管换热量的分布类型进行检验。柯尔莫哥洛夫检验法（Kolmogorov-Smirnov），简称K-S 检验法，相比卡方检验法，此种方法具有以下优点：K-S 检验可以适用于样本数量较少的情况，而卡方检验适用性较差。对于任何样本数量的情况下，发现K-S 的检验法均优于卡方检验法[11]。

K-S 的基本思想是检验根据样本观测得到的经验分布函数Fn(x)和假设的理论分布函数Fx(x)的差异。当该差异大于临界值时，拒绝样本服从某一分布函数的假设。对于某一样本容量为n 的样本，根据观测值得到的经验分布函数可以表示为：

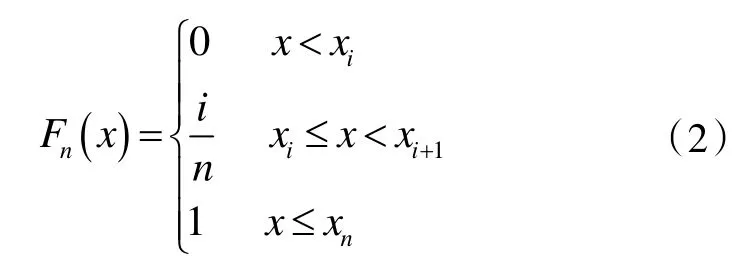
对于理论概率分布函数Fx(x)，当该分布函数并非已知时，可以借助样本均值与平均方差来代替总体分布的均值与方差[11]：

检验统计量可以表示为：

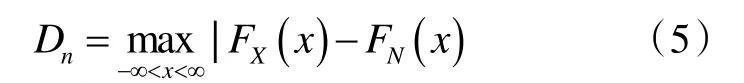
当检验统计量Dn小于临界值Dn,α时（a 为置信水平，通常取0.2），可以认为样本服从假设的理论分布。否则，则应拒绝原假设。通常情况下临界值Dn,α可通过读表取得，当置信水平a=0.2，样本数据大于100 时，Dn,α可通过如下公式计算：

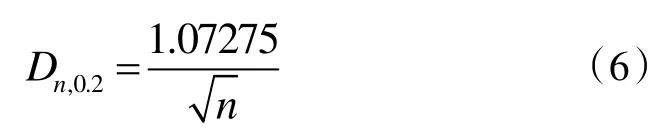
对盘管显热量，潜热量以及全热量进行正态性检验，观测值累积经验分布函数与正态分布函数的对比如图9、图10、图11，检验结果如表2 所示：

图9 全热量累积经验分布函数

图10 潜热量累积经验分布函数

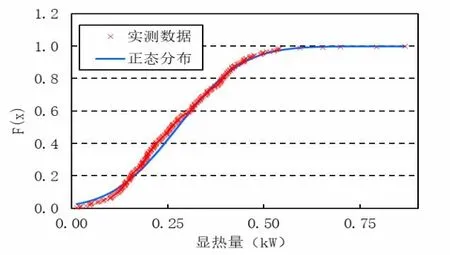
图11 显热量累积经验分布函数

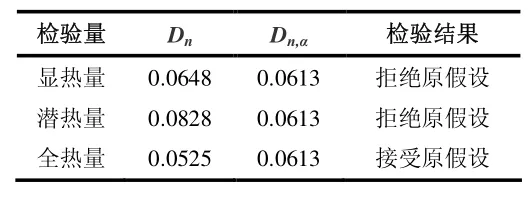
表2 K-S 检验结果

可以发现，对于盘管的显热量及潜热量，检验统计量Dn大于临界值Dn,α，拒绝显热量以及潜热量的分布符合正态分布的假设。而对于全热量，检验统计量Dn小于临界值Dn,α，接受检验统计量符合正态分布的假设，该正态分布均值1.256，方差为0.208。

5 盘管性能优化潜力分析

由于风机盘管选型问题以及实际运行工况等因素影响，盘管实际换热量并不能满足室内环境需求。因此探究提高风速对实际运行状态下风机盘管换热性能的优化潜力。借助已观测到的室内实际数据，对观测期间风机盘管高档风速下换热性能进行模拟。计算出的风机盘管逐时换热性能（显热量，潜热量与全热量），如图12、图13、图14。

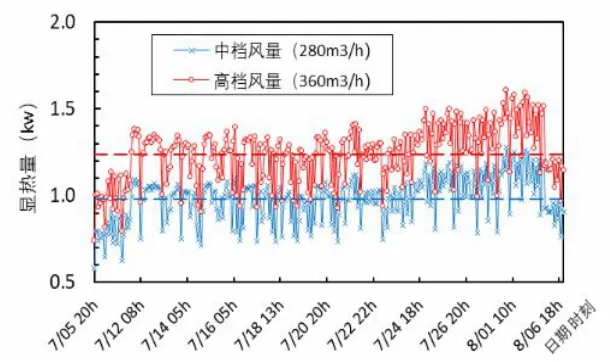
图12 不同风量下盘管逐时显热量

图13 不同风量下盘管逐时潜热量

图14 不同风量下盘管逐时全热量

可以发现，将风速从中档提到高档后，显热量平均提高26.5%，全热量平均提高20.9%。然而风机盘管除湿能力并没有提到有效提升，相比中档风量，高档风速下盘管除湿能力降低了35.3%。

6 结论

针对风机盘管实际运行中性能与额定工况存在偏差这一问题，首先建立了基于盘管热交换效率的模型，借助实测数据的验证发现，该模型可以准确计算风机盘管在实际运行中的换热情况。计算显示，风机盘管在实际工况运行中，相比额定工况，显热量和全热量分别下降10%和25%。接着，本文引入统计学方法，对换热性能分概率分布以及分布特征进行分析。可以发现，在观测期间，盘管全热量和显热量均下降接近40%。同时，借助K-S 方法对盘管换热量这一统计量进行正态性检验，可以发现，风机盘管的全热量可以看作是均值为1.256、方差为0.208 的正态分布，而显热量以及潜热量则不具备这一分布特性。最后笔者基于模型对风机盘管换热性能的优化潜力进行分析，通过模拟发现，在实际运行中可以通过调节风量来实现调节换热性能的目的：将风机风量有中档调至高档（风量提升28.6%），对于相同的室内环境条件下，可提高盘管换热显热量26.5%，全热量平均提高20.9%。