基于AAR标准的石砟漏斗车疲劳寿命评估

王 顺1, 冯国胜1, 李 龙1, 许秀峰, 吕 华

(1.石家庄铁道大学 机械工程学院，河北 石家庄 050043；2.中车石家庄车辆有限公司，河北 石家庄 051430)

“十三五”规划指出，国民经济将继续保持平稳增长。铁路是国民经济大动脉、国家重要基础设施和大众化交通工具，对于经济社会的发展具有重要支撑和拉动作用。我国幅员辽阔、内陆深广，资源以及工业分布不均衡，这方面的国情决定了铁路运输较其他交通方式相比占据主导地位。重载运输是当今铁路货物运输发展的趋势，它在降低运营成本、增强市场竞争力方面起重要作用[1-2]。根据我国铁路货车装备技术整体发展情况，货车结构的疲劳可靠性问题已经成为制约货车装备技术提升的关键因素[3]。因此，对于重载货车车体的疲劳寿命校核，具有非常重要的意义。

1 AAR标准疲劳评估简介

1.1 AAR疲劳评估原理

图1 S-N曲线图

AAR是一个非营利性技术协会，它的成立是为了确保北美铁路安全、迅速、高效、整洁、技术先进，是北美铁路协会(Association of American Railroad)的简称，主要业务为铁路货运方面以建立行业标准为基础提供技术服务，并专门为铁路货车车辆制定法规[4]。AAR标准机车车辆手册：CII分册分册[M-1001]《货车设计制造规范》[5]中提供了详细的实测载荷谱、构件疲劳参数和S-N曲线，该标准可计算出目标车辆的具体寿命。

待评估车体寿命可由图1S-N曲线图推导。

设k为S-N曲线的绝对斜率

(1)

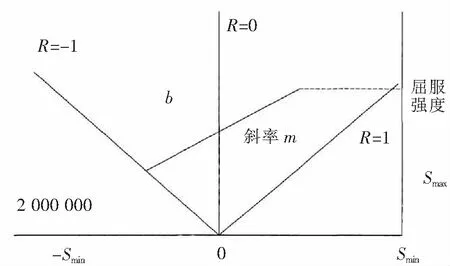
图2 理想的修正GOODMAN曲线

(2)

实际上，Smax代替Si，故方程(2)为

(3)

由于疲劳极限Se的值跟随不同的R值变化，疲劳极限方程可由理想的修正GOODMAN曲线得出,如图2。

理想的修正GOODMAN曲线方程为

Smax=mSmin+b

(4)

式中，b为R=0时的疲劳极限；m为改进的GOODMAN图的斜率。

按照定义

(5)

但是在疲劳极限时，Smax=Se，因此，可推导

按照粒子速度的频率响应函数定义，可以给出以测点半径r1、r2处球面波径向粒子速度为输入量的频率响应函数的计算公式为[13, 18, 20]

(6)

根据Miner线性累计损伤假设，当损伤增值之和为1时，认为出现疲劳破坏。那么载荷谱下出现损伤的循环数为

(7)

式中，Nt为部件在载荷谱下出现损伤的循环数；αi为每一应力级占总循环的份数；Ni该应力级时将导致损坏的循环数。

使用方程(7)可以预测适用疲劳特性的各部件达到损坏的循环数，从而计算部件的寿命

(8)

式中，β为每英里谱中循环数。

1.2 AAR疲劳评估方法

图3 AAR疲劳寿命分析流程图

进行车体部位的疲劳分析，首先应结合有限元分析结果确定分析的部位，选取位置大多是车体焊接结构附近。由于货车车头一般为焊接结构，结构焊成后不做消除残余应力的处理，疲劳强度会大幅度低于金属本身[6-7]。根据AAR标准查找评估部位相关的母材或者焊缝具体参数，其中包括b、m、k或者Se的数值，载荷与载重呈线性关系，由AAR标准提供的重﹑空车垂向心盘载荷谱﹑纵向拉压和扭转载荷谱分别换算出车体各处在这些载荷谱作用下的应力幅值谱。根据原理方程进行单一工况下的损伤计算，评估出该工况下的寿命后，利用多载荷通道疲劳寿命计算方法近似处理这种多载荷事件，计算该部位在各工况下的综合疲劳寿命[8]。计算流程如图3。

2 车体疲劳寿命分析

2.1 车体有限元模型的建立

漏斗车三维尺寸为：纵向长度11 570 mm，横向宽度2 492 mm，心盘到车顶的高度2 150 mm。为了得到高精度的有限元模型，先由三维软件SolidWorks对其进行必要的简化，在保留车体结构特点和力学性能的前提下，略去小尺寸的非承载构件，忽略零件表面小孔及圆角等特征，简化结果见图4。

建立好几何模型，导入有限元分析软件ANSYS Workbench中。材料选用Structural Steel，由于模型零件几何特征规则，选用自动分网的方法，单元形式采用壳和实体混合。有限元计算精度随着网格的变小而提高，但同时对于计算资源的占用也会增加。为得到适当的网格尺寸，选用试算法，将网格细化到一定程度，以应力结果偏差为指标来确定最终模型，划分结果如图5所示，其单元数54 322，节点数103 002。

图4 漏斗车三维模型

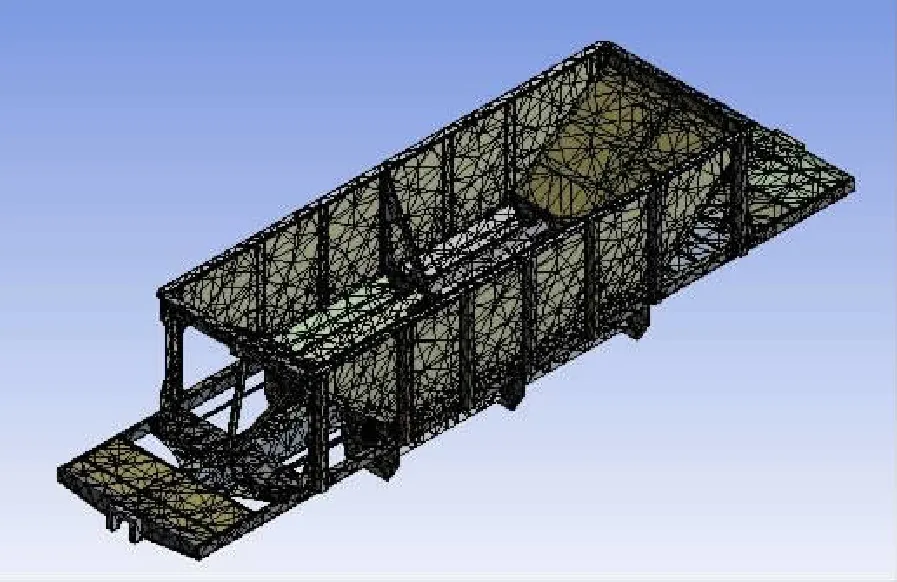
图5 漏斗车有限元模型

2.2 约束设置

为使边界条件与静强度实验条件最为接近，在车体一侧心盘处施加固定端约束，另一侧心盘约束X和Z轴方向的位移并在Y向施加弹性约束[9]。模型中坐标轴的方向为：车体横向为X轴，纵向为Z轴，垂向为Y轴。

2.3 有限元模型计算

根据AAR标准规定，在车体相应位置施加载荷，计算求解出车体在垂向静载、纵向100 t拉伸、纵向100 t压缩和40 kN·m扭转4种工况下的应力，各工况应力云如图6～图9。

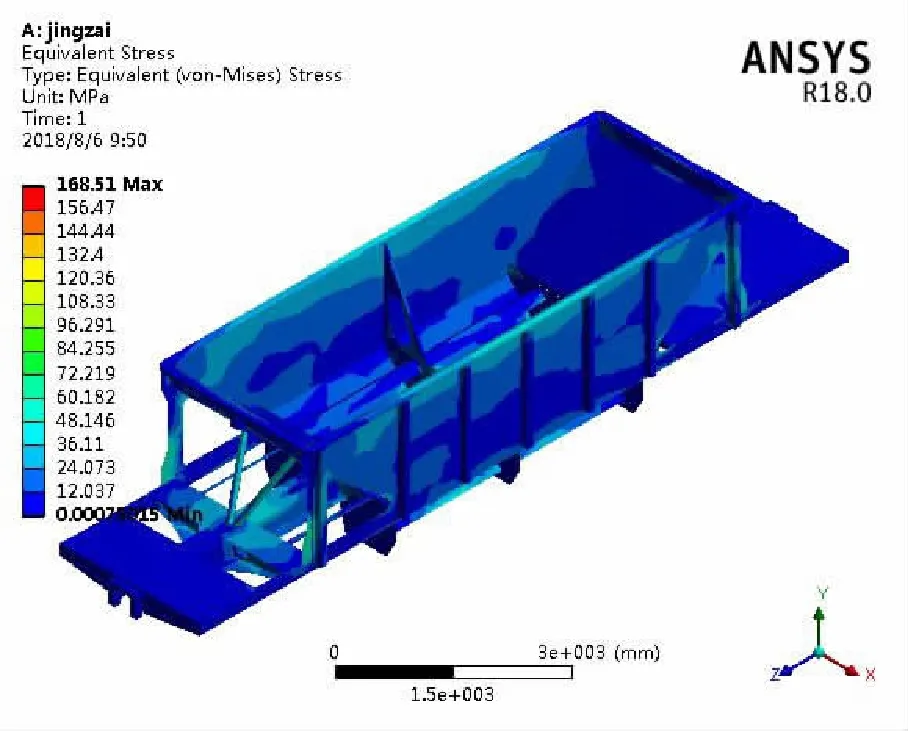
图6 垂向静载应力云图

图7 纵向100 t拉伸应力云图

图8 纵向100 t压缩应力云图

图9 扭转应力云图

基于分析结果，在应力集中较大的焊缝附近选取了11处部位，提取相应的4个工况的Von.Mises 应力，如表1。

表1 11个部位对应Von.Mises应力 MPa

注：应力低于5 MPa，损伤计算忽略不计，表中记为0。

2.4 疲劳寿命计算

AAR标准中涉及到的部分评估部位相关焊缝的疲劳特性见表2。

表2 钢制构件焊缝的疲劳特性

由于涉及车体部位较多，手工计算较为不便，因此使用数据分析软件Matlab进行数据处理。根据表1提供的11个部位的结构特征，在AAR机务标准查询相应的材料疲劳特性，将分析用到的重、空车各载荷谱数据按列依次放入Excel表格中，Matlab程序将其作为输入文件读取。根据编写的Matlab程序，m文件中依次输入b、m、k、载荷、应力值和每英里平均循环次数，经过2次判断过程，可以计算出评估位置在各工况作用下车体疲劳寿命评估结果。最后利用多载荷通道疲劳寿命计算方法计算该部位在各工况下的综合疲劳寿命。

2.5 车体疲劳寿命预测

该漏斗车的设计寿命为30 a，年运营里程按15万km计算，则该车车体结构的疲劳设计寿命450万km以上，该重、空车里程比取为1∶1。本次车体的疲劳寿命按该运营情况计算。

通过计算，车体结构在AAR载荷谱下的疲劳损伤估算见表3。

表3 米轨漏斗车疲劳寿命计算结果 km

3 结论

从表3中寿命评估结果看，大部分的部位寿命评估结果远高于预期寿命。母材的寿命一般高于焊缝，其中最薄弱的部位是二位枕梁下盖板与下侧梁间搭接焊缝，预测寿命约为667万km，满足预期寿命450万km的设计要求。其余薄弱部位寿命如：漏斗板与漏斗端隔板间焊缝3 680万km，端墙斜撑左与腰带处焊缝1 780万km，均远高于预期寿命。

AAR标准用来评估货车寿命，用到的载荷谱数据较多，计算步骤繁琐。涉及评估国内货车寿命时，更需要用到单位换算，用Matlab编程处理计算数据代替手工，极大地提升了计算效率，亦减少出错的可能性。