柔性人行悬索桥空间索面抗风缆索系统的找形计算方法

(山西省交通规划勘察设计院有限公司，山西 太原 030006)

0 引言

随着我国经济水平的不断提高，越来越多的景区内修建了大跨度柔性人行悬索桥。这种桥的桥面宽往往不足3 m，但跨度却在100 m以上，这导致其横向刚度和承载力很小，无法依靠自身来抵抗横向风荷载。为此，工程上常在桥面两侧增设抗风缆索系统来提高结构横向刚度[1]。在以往工程设计中，抗风缆索系统的设计计算方法较为简单：利用简化抛物线理论对风缆单独进行计算[2-3]，不考虑风缆与结构的相互作用。这种将风缆与主结构分割开来简化计算的做法，用于抗风缆索系统自身的设计并没有太大问题，但这种做法不能考虑风缆对主结构竖向拉力影响，也无法查看抗风缆索体统对整个结构横向刚度的贡献程度。若将抗风缆索系统与主结构一起建立有限元模型进行分析，则可考虑风缆对主结构的影响，并可查看主结构和抗风缆索系统对横向风荷载的分担比例。为实现这一目的，首要解决的问题就是抗风缆索系统的找形问题。

文献[4]利用ANSYS迭代结算得到风缆的成桥线形，但采用的是简化抛物线理论，文中按照风荷载的大小确定成桥状态风缆系统线形，恒载状态下风缆的变形较大。严格按照精确悬连线单元理论编写恒载状态下风缆系统的线形，本质上为解析解。

按照先平面后立面的顺序给出空间索面抗风缆索系统的找形思路和过程。在平面内由于没有自重力的影响，可借助节线法求解；在立面内由于有单元自重的影响，需采用悬连线索单元求解。文中给出计算迭代流程并利用Matlab编程实现。工程实例计算结果表明，本文提出的找形方法快速有效，可供同类项目参考。

1 平面

设置抗风缆索的目的是抵抗横向风荷载并提高整个结构横向刚度，抗风主缆和桥面系之间通过抗风拉索连接起来，并向桥面系传递竖向力、横向力及纵向力。抗风拉索一般通过滑轮实现与桥面系及抗风主缆之间的连接，所以抗风拉索的轴力理论上是不发生变化的。但由于索段自重和节点处竖向集中力的影响，各段之间的轴力还是略有不同的，在水平面内由于没有其他外界荷载的影响，抗风拉索轴力在水平面的分力是一致的，图1为抗风缆索平面投影布置示意图。

图1 抗风缆索平面投影示意图

1.1 水平面内找形推导

图1中Si为抗风拉索与桥面系相连节点的横向坐标，共n个，为已知值；ai为抗风拉索沿纵桥向的投影长度，共2n个，为已知值；bi为抗风主缆索段长度沿纵桥向的投影长度，共n+2个，为已知值；Yi为抗风主缆节点的横向坐标，共n+3个，其中起终锚固点横向坐标Y0、Yn+2以及“垂点”的横向坐标Ykey是人为设定值，其余n个Yi值为未知值；F为抗风拉索轴力的平面投影分力，为设定值；Hxi为抗风主缆轴力的纵桥向分力，共n+2个，为未知值。

利用接线法[5]的思想求解主缆节点的横向坐标，即对Y1～Yn+1各节点分别进行纵向和横向受力平衡计算，共有以下2n+2个方程式。

(1)

以上2n+2个方程中有2n+2个未知量，其中包括n个主缆横向坐标Yi(Ykey为已知量)和n+2个主缆轴力的纵向分力Hxi，正好可以求解，但以上方程组与传统的可一次求解的接线法[5]有所不同，此处未知量Yi与Hxi之间呈耦合关系而不是线性关系，不可直接线性求解。

从方程组(1)可以看出，如果已知第1段主缆轴力的纵向分力Hx1和第一点的横向坐标Y1就可以逐步推求出其他索段的纵向分力和节点横向坐标，而主缆终点和“垂点”的横向坐标是已知值，因此可以先假定一组Hx1和Y1为已知值进行计算，如果求得的终点和“垂点”的横向坐标与设计值差距很小时，可认为Hx1和Y1就是所求未知量的解。

1.2 水平面内迭代求解

在具体求解方法上，可以假定一个Hx1值，将一系列的Y1值代入方程组试算，求解各节点的横向坐标，当终点坐标的计算值与设计值差距足够小时，认为Y1为此Hx1值下的真值。但此时“垂点”的横向坐标的计算值与设计值不一定吻合，这时就需要更新Hx1值，再重复之前的计算过程，直至“垂点”的横向坐标与设计值的差值足够小时，整个过程是个大循环内套小循环不断迭代试算的过程，这个过程可用二分法来实现，具体的迭代流程如图2。

在迭代过程中，利用了2个基本原理来调整初始值Hx1和Y1的更新方向，以便快速收敛，即：

(1)主缆纵向水平分力Hx1越大则“垂度”越小；

(2)初始横向坐标Y1越大则终点的横向坐标也会越大。

1.3 水平面内迭代流程

根据实现上面提到的求解方案，绘制抗风缆水平平面内找形的流程如图2，可用Matlab编程实现。

图2 抗风缆索平面找形迭代流程图

2 立面

平面计算收敛后，平面的线形就确定了，利用简单的几何关系便得到主缆和拉索在水平面内的投影长度和沿平面轴向方向的分力，这将作为立面找形计算的已知值，抗风缆索的立面投影示意见图3。

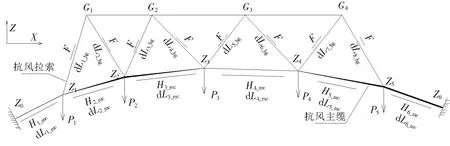
图3 抗风缆索竖面投影示意图

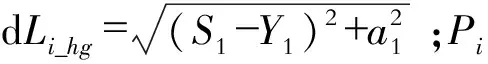
2.1 索单元假定

缆索在立面的线形受到缆索自身重力的作用，在节点间呈分段悬连线，必须采用精确悬连线理论进行计算才能反映真实的缆形，精确悬连线索单元理论的假定如下：

(1)索单元仅承受轴向拉力，不承受压力和弯矩，为理想柔索。

(2)主缆仅仅承受沿无应力索长的均布力和节点处的集中力。

图4 索单元计算简图

(3)忽略索单元截面的横向变形，认为截面不发生变化。

索段的计算简图如图4，其中竖向坐标以向上为正，外力的方向与坐标一致时为正值。根据以上基本假定和受力平衡得到索单元的基本方程

Hx1=-Hx2

(2)

V2=-(V1+qS0)

(3)

(4)

(5)

式中，S0为索单元无应力长度；q为沿无应力长度的竖向均布力；H1、V1为索起点端受到的纵向和竖向分力，力的方向与坐标系统保持一致；E为索单元材料弹模；A为索单元截面面积；dx为索单元在水平面内的投影长度；dz为索单元终点竖向坐标减去起点竖向坐标。索单元的基本参数为S0、Hx1、V1、dx、dz，只要已知其中的3个参数，就能求得剩余的2个参数，这个过程也需要迭代求解，具体过程可参考文献[6]。

2.2 立面找形推导

立面线形求解过程也是计算各节点受力平衡的过程。各节点受到的力包括主缆起终点传来的竖向、水平分力和拉索起点传来的竖向、水平分力以及节点所受竖向集中力(如索夹重)。其中主缆和拉索传递给节点的水平分力是已知值，且经过平面的找形计算，已在节点处保持了平衡，所以在本阶段可不考虑，仅关注竖向受力平衡即可，各节点竖向受力见图5。

图5 各节点竖向受力

索单元为5参数非线性单元，要已知3个参数才能计算另外2个，而各索段的轴力水平分力H和水平面投影长度dL已在平面计算阶段获得，需要另外一个参数才能启动计算，故先假定Z1=Z0+dZ1为已知值。这样1号主缆的便获得了已知值dz1_mc，加上平面计算获得的另外两个值H1_mc和dL1_mc，正好3个参数，利用索单元基本方程可求得剩余的两个参数V1_mc和S01_mc；1号拉索获得已知值dz1—hg=g1-Z1，加上平面计算获得的另外两个值F和dL1_hg，正好3个参数，利用索单元基本方程可求得剩余的两个参数V1_hg和S01_hg；利用节点竖向受力平衡：q1+Vq1_hg+Vz1_mc+Vq2_mc=0，可得第二段主缆的起点竖向力Vq2_mc。

第二段索获得3个已知参数H2_mc、L2_mc、Vq2_mc，利用索单元基本方程可获得剩余参数dZ2、S02_mc，这样第二点的竖向坐标可确定Z2=Z1+dZ2；2、3号拉索分别获得已知值dz2—hg=g1-Z2、dz3—hg=g2-Z2，加上平面计算获得的F、L2_hg、L3_hg，可获得剩余参数Vq2_hg、Vq3_hg、S02_hg、S03_hg，同样利用节点2竖向受力平衡，q2+Vq2_hg+Vq3_hg+Vz2_mc+Vq3_mc=0，可得下一段段主缆的起点竖向力Vq3_mc。

依次类推可得到最终点竖向坐标计算值Zn+2_cal，这个值与终点竖向坐标的设计值Zn+2会有所差别，这就要不断迭代调整初始dz1_mc，直到两者差值足够小，计算结束后可获得主缆竖向坐标和各索段的无应力长度。dz1_mc的初始值可根据线性节点平衡法[3]获得，较精确的初始值和适当的步长可加快收敛。

3 算例

某景区人行悬索桥，主缆跨度125 m，垂度12 m，吊杆间距3 m，见图6。为抵抗横向风载，在跨中103 m段设置抗风索缆结构，抗风拉索成三角形布置，通过滑轮与桥面系及抗风主缆相连，恒载状态设计抗风拉索轴力的水平面分力为0.5 kN，抗风拉索长度的纵向分量为3 m。抗风主缆起终锚固点距拉索上节点的竖向距离6.7 m，横向距离8.5 m，横向垂度为7.5 m。单根主缆由7根6×19s+IWR(Φ36)型钢丝绳组成，弹模1.1e5 MPa；吊杆采用Φ32粗钢筋，弹模2.06e5 MPa；抗风主缆为单根6×19s+IWR(Φ36)型钢丝绳，弹模1.1e5 MPa；抗风拉索为单根6×19s+IWR(Φ16)型钢丝绳，弹模1.1e5 MPa。

图6 某人行悬索桥布置图(单位:cm)

抗风拉索与桥面系交点共17个，抗风拉索共2×17=34节，抗风主缆共17+2=19节，节点17+3=20个，以第10个节点作为横向“垂点”，设计抗风拉索成桥状态的平面分力为0.5 kN。利用Matlab编制找形程序，得到抗风主缆的横、竖向坐标及无应力长度见表1。

表1 抗风主缆的节点坐标和无应力长度 mm

4 验证

利用Matlab编制的找形程序，不仅能得到成桥线形、索段无应力长度，还能得到拉索对桥面系的竖向作用，将该竖向力作为外荷载施加于MIDAS软件建立的主结构有限元模型中进行主缆找形。最后将找形成功的主结构模型与抗风缆索结构模型合二为一，并去掉之前施加的竖向力，打开大位移选项进行几何非线形分析，得到的恒载状态变形结果如图7，可见恒载状态下结构的位移量很小，横竖向位移量分别为2.3 mm、1.95 mm，不足跨度的1/40 000，说明本文提出的抗风拉索找形方法满足工程精度要求。

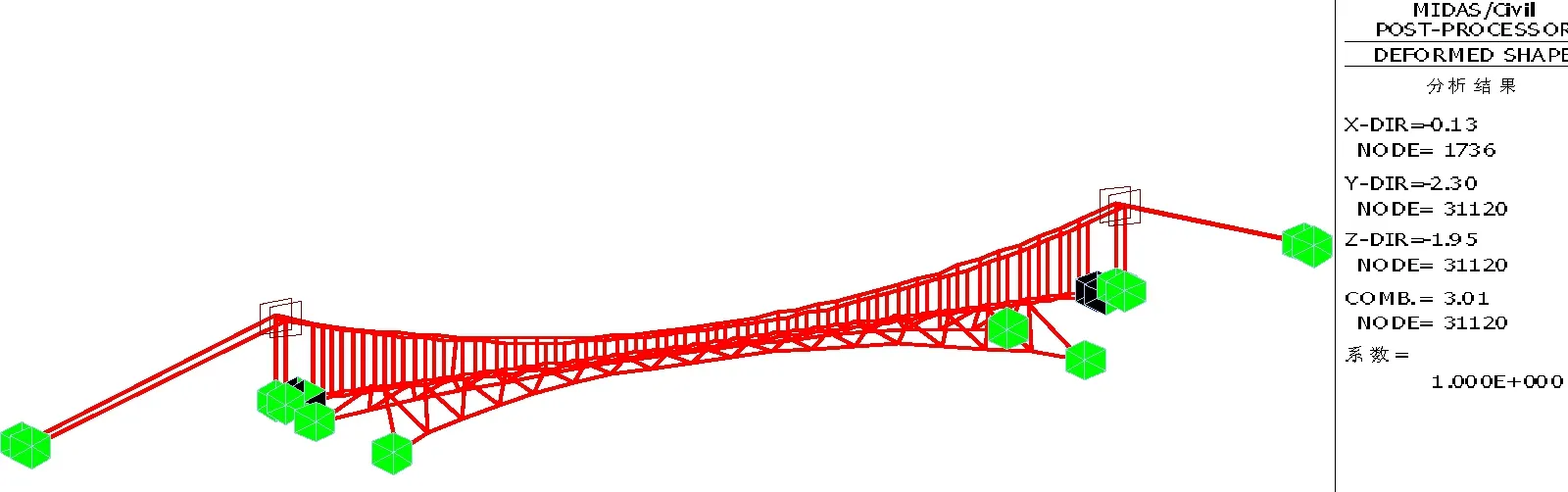
图7 恒载状态整体结构的变形(单位:mm)

5 结语

(1)按照本文提出的方法编程计算，可快速找出空间索面抗风缆索系统的成桥线形。

(2)基于分段精确悬链线索单元求解得到的抗风缆成桥线形及各索段无应力长度，本质为解析解，带入有限元模型进行几何非线性分析，计算结果表明，恒载状态下缆索系统变形很小，精度可满足工程要求。