贝雷梁钢便桥动力响应影响因素分析

(黔南民族职业技术学院 建筑工程与设计系，贵州 都匀 558000)

0 引言

贝雷梁钢便桥以自重轻、方便快速架设等优势在工程中得以广泛应用，尤其在抗震抢险救灾的时候，作为架设运送物质的便桥起到了关键作用。近年来，对于贝雷梁的结构安全计算，大多数实际工程采用静力分析的方法来保证[1-5]。贝雷梁钢便桥作为临时桥梁结构使用时，一般需要满足大型重载车辆的通过，当车辆以某一速度通过时，桥面不平顺等因素会引起车辆与贝雷梁结构之间发生耦合振动，产生的变形和应力都比荷载静止不动时大，忽略动力效应可能造成结构承载力降低，导致结构破坏。黄文等[6]结合工程实例对贝雷梁桥梁静动载试验，提出限载限行，加强结构的建议；袁红茵等[7]通过静动力荷载试验实测得到动力特性规律性较差，振动异常明显，尤其是水平振动；陈鲁等[8]通过5种工况满载试验，分析了钢便桥的承载力特征；李皓桢等[9]利用ANSYS对贝雷桁架架桥机进行模态和谐响应的分析，得到设计架桥机时应避免的两阶频率。以上学者的研究揭示了贝雷梁钢便桥的一些动力响应特性，让工程师在面对实际工程时得到很好的应用，但贝雷梁的加强弦杆及车辆的移动速度对钢便桥的动力影响没有进行分析，给实际工程应用带来困惑。

在进行贝雷梁钢便桥的结构计算时，多数将计算模型简化为二维平面模型，即假设贝雷梁均匀承担来自横梁的竖向荷载，并没有考虑贝雷梁因三维空间原因产生的不均匀承载效应。其计算结果在一定程度上反应了贝雷梁钢便桥的动力特性，但没有反应贝雷梁钢便桥的三维整体振动状态。本文利用ANSYS有限元分析软件，建立三维空间有限元模型，从模态分析中得到主要的振动形态，进而考虑不同车速、不同弦杆的加强方案，对贝雷梁钢便桥动力响应的影响进行分析研究。

1 贝雷梁钢便桥

根据文献[10]知，贝雷梁钢便桥主要由主梁(桁架)、桥面系、支撑系统、引桥和人行道组成。贝雷片用销子连接成一排贝雷梁，利用支撑架连接贝雷梁组成主梁，布置在桥梁两侧，两侧主梁用横梁连接，在该横梁上铺设无扣纵梁和钢板形成桥面系。选取跨度为24 m(8片贝雷片)的下承式简支梁钢便桥作为研究对象，采用4种不同弦杆加强方案，分别为无加强弦杆、上弦杆加强、下弦杆加强和上下弦杆加强，具体尺寸及加强方式如图1所示。贝雷片的弦杆、竖杆及斜杆均采用16Mn钢；横梁为27号压延工字钢制成；纵梁由热轧轻型10号工字钢和8号工字钢制成；桥面板采用5 mm厚钢板制成；加强弦杆为2根10号槽钢组成，与贝雷片弦杆相同。

图1 贝雷梁钢便桥横断面图(单位：cm)

2 三维空间有限元模型

按照上述钢便桥的实际尺寸，运用大型有限元软件ANSYS建立相应的三维空间有限元模型。利用梁单元beam188模拟主梁结构和壳单元shell63模拟桥面系结构，桥面系和横梁、横梁和主梁的连接采用3个方向移动自由度的耦合关系，贝雷片之间采用锥销将阴阳接头连接起来，在平面内方向的连接为铰接，故采用3个方向移动自由度和2个旋转自由度的耦合关系，即假设各构件之间的连接无滑移、无空隙，并忽略因连接的缝隙而产生的挠度，桥梁两端支座边界条件设置为铰接，三维空间有限元模型如图2所示，包含27 587个节点和20 024个单元。材料的弹性模量为206 GPa，泊松比0.3，密度7 850 kg/m3，结构阻尼比为0.03。在车辆通过钢桥时，因路面不平顺等原因，会激起车辆的振动，继而激起桥梁振动，实际整个过程是车桥耦合振动，为了简化计算，假设车辆为无质量的匀速移动荷载，其中前轴轴重30 kN，中轴轴重2×120 kN，后轴轴重2×140 kN，移动荷载模型[12]如图3所示，车辆轴线与桥梁轴线重合，即不考虑车辆偏心。

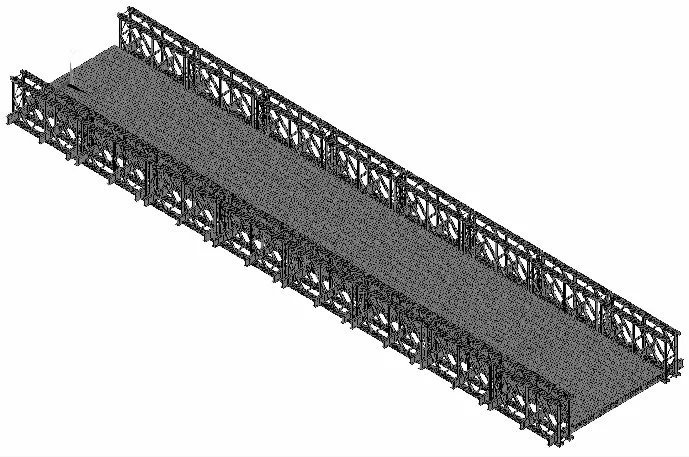
图2 贝雷梁钢便桥三维空间有限元模型

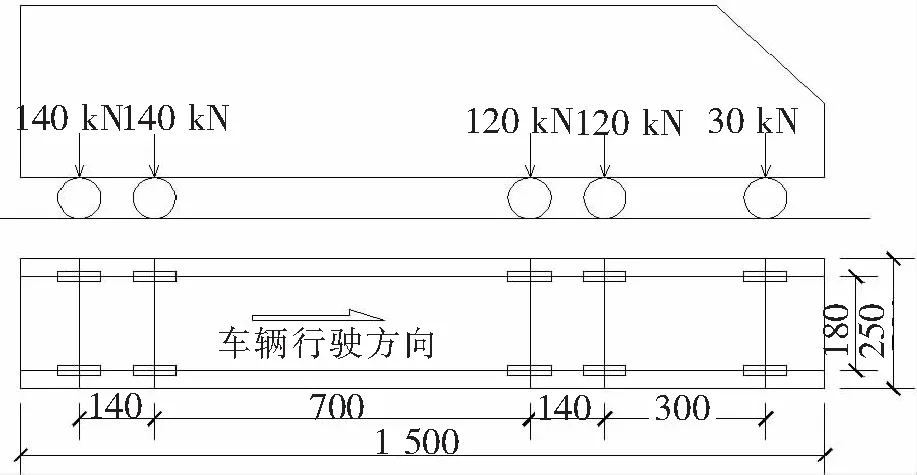
图3 移动荷载模型图(单位：cm)

3 数值试验分析

首先对贝雷梁钢便桥结构的固有特性进行分析，即模态分析[11]，分析采用Block Lanczos法，选取前10阶模态，经过软件计算，得到无加强弦杆的前4阶主振型变形如图4所示。为了研究加强弦杆的影响，建立4种不同加强方案的有限元模型，分别为无加强弦杆(上下弦杆为2[10)、上弦杆加强(上弦杆2[10，下弦杆4[10)、下弦杆加强(上弦杆4[10，下弦杆2[10)和上下弦杆加强(上下弦杆为4[10)，数值分析得到前10阶振动模态，取不同加强方案的前3阶[9]固有频率和主振型进行分析，如表1所示。

图4 第1～4阶模态图

表1 不同弦杆加强方案的贝雷梁钢便桥前3阶模态频率及主振型

从表1的数据来看，第1阶固有频率在4.2～5.2 Hz之间，加强弦杆对钢桥结构的固有频率有所提高，但主振型并没有改变，前2阶的振动形式均为竖向弯曲振动为主。说明加强弦杆能够提高钢桥结构的刚度，提高其固有频率，并未改变钢桥的基本结构。车辆通过钢桥最容易发生的均是竖向的弯曲振动，在车辆通过钢桥时，其激励源主要来自车辆工作频率及路面不平顺，可以通过假设移动荷载为随时间变化的正弦函数来模拟，即Fsin(wt)，其中，w为激励频率，故要求车辆激励荷载的频率应尽量远离钢桥的第1阶固有频率，以避免与钢桥发生共振现象而导致破坏。

为了进一步研究车速、加强弦杆等因素对钢桥振动加速度及动位移的影响，采用ANSYS的瞬态动力分析方法[11]，对4种不同弦杆加强方案的有限元模型进行数值模拟。采用移动荷载模拟整个车辆从右侧上桥直至下桥的过程，每个荷载步荷载移动0.5 m，包含5个荷载子步，时间间隔等于0.5除以车辆移动速度，共计76个荷载步文件求解。通过钢桥的最大竖向位移及振动加速度等动力响应分析其因素的影响。

取车辆模型的移动速度在0～72 km/h之间进行瞬态分析。由于结构和荷载均对称，得到左右两边主梁的响应相同，提取任意一边主梁的内外两侧贝雷梁的最大竖向位移，此时车辆前轴钢桥上桥端20 m处附近，随速度变化如图5所示。从图中可见，随着车速的增加，最大竖向位移均逐渐增大，从增大的趋势来看，由快到慢依次是无加强弦杆、下弦杆加强、上弦杆加强和上下弦杆加强，受速度影响最小的是上下弦杆加强的模型，相对而言，上弦杆加强优于下弦杆。任何一种弦杆加强模型的两排贝雷梁变形并不是完全一致的，而且内侧贝雷梁的变形较大，说明两排贝雷梁受力并不均衡，内侧贝雷梁因变形大而承担相对较多的荷载。取4种弦杆加强模型内外侧贝雷梁变形量差值分别占平均值的1.34%、1.78%、1.37%、0.98%，从所占比值来看，内外侧贝雷梁的不均匀变形差异较小，且上下弦杆加强的模型能够减小差异，仅仅加强上弦杆或下弦杆不能起到减小内外侧贝雷梁变形的差异，相反会增大差异，造成内外侧贝雷梁的变形不一致，相对而言，仅仅上弦杆加强会更不利于贝雷梁的均匀受力。从数值差异大小上来看，内外侧贝雷梁的变形差异的数值非常小，故可忽略不计。按照规范[12]的最大允许竖向位移为L/500，即48 mm，仅有上下弦杆加强的模型刚度满足其要求。

图5 跨中最大竖向位移变化图

跨中截面的动位移是反应结构振动幅值的重要参数。图6给出了最大动位移的变化曲线，可以看到，贝雷梁钢便桥最大动位移与速度呈非线性的增大关系，尤其是无加强弦杆的动位移最大，相对而言，上下弦杆加强大约能够降低动位移三分之二，上弦杆或下弦杆加强的动位移处于两者之间，且上弦杆加强的动位移明显低于下弦杆加强。说明贝雷梁钢便桥的振动幅值随着车速的提高逐渐增大，加强弦杆能够降低钢桥的动位移，提高钢桥的刚度，在贝雷梁的上弦杆使用加强弦杆优于下弦杆。钢桥本身刚度较差，使用上下弦杆均加强能够明显降低速度对钢桥动位移的影响。

跨中竖向最大振动加速度出现在车辆前轴达到13.2 m处位置，其变化规律如图7所示。随着车辆移动速度的增大，贝雷梁钢便桥的跨中竖向最大振动加速度也会随之增大，钢桥竖向最大振动加速度在车速低于50 km/h时变化不大，超过50 km/h时，钢桥的竖向最大振动加速度也开始增大，相对而言，加强弦杆能够降低钢桥竖向最大振动加速度，尤其是车速较高时，加强弦杆的作用更加明显地起到减小车速对最大振动加速度的影响。上弦杆或下弦杆加强在速度为10～50 km/h时稍微有些区别，而车速不在这个区间时上侧或下侧加强均一样，如车速达到72 km/h，仅仅在上弦杆或下弦杆使用加强弦杆能降低最大振动加速度30%，上下采用加强弦杆能够降低50%。从以上分析来看，加强弦杆能够降低钢桥的跨中竖向最大振动加速度，减小钢桥动力响应，为使得贝雷梁钢便桥动力响应不至于迅速增大，故建议车速低于50 km/h，以避免桥梁产生过大的振动加速度而发生破坏。

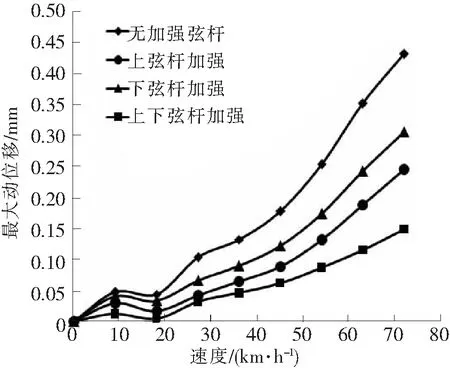
图6 最大动位移随速度的变化图

图7 跨中竖向最大加速度变化图

4 结论

在贝雷梁钢便桥模态分析的基础上，对钢桥的三维空间有限元模型进行瞬态分析，通过分析最大竖向位移、跨中动位移及最大振动加速度等动力响应得到如下结论：

(1)前2阶振型为竖向弯曲上下振动，第3阶振型为侧向弯曲，荷载激励频率应尽量避免与钢桥固有频率4.2～5.2 Hz靠近，以防止出现钢桥共振，使用加强弦杆能够提高钢桥固有频率，但不能改变其振型。

(2)贝雷梁竖向最大位移随着车速的增大而增大，内外两侧贝雷梁的变形不一致，且变形差异微小，加强弦杆对其变形不一致的改善几乎不起作用，可忽略不计。

(3)动位移随速度的变化呈现非线性的增大关系，使用加强弦杆能够降低动位移，且在上弦杆使用加强弦杆优于下弦杆，鉴于贝雷梁刚度本身较低，建议作为钢便桥使用时，上下弦杆均需要使用加强弦杆提高其刚度，减小动位移。

(4)钢便桥振动加速度随着车速的增加呈非线性的增大，采用加强弦杆能够降低车速对钢桥的振动加速度，尤其是随着车速超过某值后，不采用加强弦杆的钢桥振动加速度会明显随车速增大而迅速提高。

综上所述，建议贝雷梁作为钢便桥使用时，采用上下加强弦杆，限速50 km/h，以降低钢桥的振动影响，确保车辆安全通过钢桥。