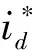一类含分数阶微积分时滞微分方程的解的指数估计
(石家庄铁道大学 机械工程学院,河北 石家庄 050043)
0 引言
分数阶微积分建模已经广泛应用于生物学、力学、控制等众多领域[1-2]。由于分数阶控制比整数阶控制能取得更好的控制效果,越来越多地被应用于实际控制中[3]。在控制系统进行闭环反馈控制时,系统中不可避免的存在时滞[4],而且时滞现象的存在会在一定程度上影响受控系统的稳定性。时滞系统广泛存在于各个工程领域,因此吸引了众多学者的关注。胡海岩等[5]从动力学的角度对时滞动力系统的研究进展进行了综述。王在华等[6]还综述了时滞动力系统稳定性与分岔方面的研究进展。张舒等[7]对耦合时滞诱发的动力学研究进展进行了综述。
在分数阶控制系统中,研究分数阶微分方程的解析解或近似解析解具有重要的理论意义。而分数阶微分方程解的存在唯一性是研究方程解析解或近似解析解的前提[8]。蒋威[9-10]研究了退化时滞微分系统的可解性,给出了通解形式,推导并证明了解的指数估计。刘可为等和Zhang X[11-12]证明了分数阶线性时滞微分系统的解存在且唯一,并推导了在有限区间内解的指数估计,给出了此类微分方程的通解形式。本文对基于电流环分数阶PID控制的永磁同步电机进行分析和建模,得到一类含分数阶微积分的时滞微分方程。对此类时滞微分方程的解的存在唯一性进行证明,并利用广义的Gronwall不等式[13],给出了解的指数估计的形式。
1 准备知识
定义1:设f(t)∈C[a,∞),实数β>0,当t>a时,可积函数f(t)的β阶Riemann-Liouville积分表示为
(1)
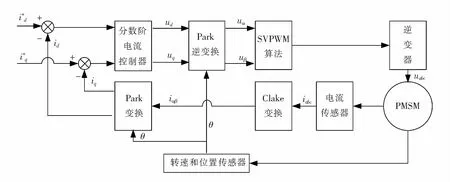
定义2:设0≤n-1<α (2) 引理1:设x(t)∈Rn是下列方程的解 (3) 式中,A,B∈Rn×n,x(t),f(t),φ∈Rn。 根据文献[9]可知方程存在唯一解 (4) 引理2(Gronwall不等式):u(t),α(t)是在区间[a,b]上的连续实值函数,β(t)≥0而且在[a,b]上是可积函数,若 (5) 则有 (6) 如果α(t)还是非减函数,则有 (7) 引理3:函数f(t)=at1-α+bt1+δ-a(1-τ)1-α-b(t-τ)1+δ-aτ1-α+bτ1+δ在区间[τ,+∞]上存在最小值f(τ)=0。其中a>0,b>0,0<α<1,0<δ<1 。 证明 f′(t)=a(1-α)[t-α-(t-τ)-α]+b(1+δ)[tδ-(t-τ)δ] (8) (1)0<τ<1,当t∈[τ,1]时,f′(t)<0,函数递减;当t∈[1,+∞)时,f′(t)>0,函数递增。在区间[τ,+∞)上存在极小值f(τ)=0。 (2)1<τ,当t∈[τ,+∞]时,f′(t)>0,函数递增。在区间[τ,+∞)上存在最小值f(τ)=0。证毕。 永磁同步电机矢量控制的核心思想是将电机的三相电流、电压、磁链经过Clake坐标变换和Park坐标变换变到以转子磁链定向的两相参考dp坐标系。其中定子电流经变换被分解为相互正交的2个分量:一个分量与磁链方向相同,代表了定子电流的励磁分量;另一个分量与磁链方向正交,代表了定子电流的转矩分量。矢量控制就是维持定子电流的励磁分量不变,控制其转矩分量,这种控制方式类似于直流电机控制中维持励磁电流不变,通过控制电枢电流来控制电机的转矩。矢量控制方法能使系统具有较好的动态特性。 有关参数如表1所示。 表1 永磁同步电机有关参数 永磁同步电机的矢量控制模型为 (9) 式中,Rs、RΩ、Ld、Lq、ψf、J、Pn分别为定子电阻、电机阻尼系数、直轴电感、交轴电感、定子磁链、电机转动惯量、极对数。 永磁同步电机电流环控制原理如图1所示,控制对象包括PWM(脉冲宽度调制)逆变器(包括PWM信号形成、延时、隔离驱动及逆变器)、永磁同步电机的电枢回路、电流采样和滤波电路。 图1 电流环控制原理图 永磁同步电机的数字伺服控制系统存在固有延时,系统的固有延时包括PWM逆变器延时(Tpwm),电流采样延时,滤波电路延时等。其中起主导作用的延时包括采样延时和逆变器输出延时,这2种延时决定于数字伺服系统所应用的采样方式及PWM占空比的更新方式。 在伺服控制系统应用中,有2种电流采样时序方式:单次采样单次更新占空比方式(SSSU)以及双次采样双次更新占空比方式(DSDU)。其中SSSU方式根据采样时刻的不同又有2种采样模式,载波周期中点时刻采样与载波周期起始时刻采样,分别记为SSSUM1模式和SSSUM2模式。 根据平均值等效原则,永磁同步电机伺服控制系统的3种固有延时分别为:SSSUM1模式的延时τ1=2Tpwm,SSSUM2模式的延时τ2=1.5Tpwm,DSDU方式的延时τ3=0.75Tpwm。 (10) 整理得电流环分数阶PID控制的数学模型为 (11) 证明:由分步法,当t∈[0,τ]时 (12) 由引理1可知时滞微分方程在t∈[0,τ]上存在唯一解,表示为 (13) 当t∈[τ,2τ]时,此方程也存在唯一解,表示为 (14) 以此类推,假设方程在区间[(k-1)τ,kτ],k∈N+上的解为xk(t),则根据引理1,可得x(t)在区间[kτ,(k+1)τ]上有唯一解,为 (15) 即时滞微分方程(12)在区间[0,+∞]上的解存在且唯一,证毕。 在方程的解存在且唯一的情况下,推导此类含分数阶微积分的时滞微分方程的解的指数估计。 定理2:设x(t)是时滞微分方程的解,且n维列向量φ(t)∈C([0,+∞)),0<α<1,0<δ<1 。则方程的解存在且唯一,并且解在[0,kτ]上有以下形式的估计 (16) 式中,矩阵A,B,C,E的范数取其行列式的最大特征值,矩阵的范数分别记为σa、σb、σc、σe;σmax=σc+σb,‖x(t)‖是向量x(t) 的矩阵范数,‖φ‖=sup|φ(t)|,σf是向量F的最大范数。 证明:对式(12)两边进行积分,当0≤t≤kτ时,有 (17) 则有 (18) (19) (20) 由引理3可知 (21) 故当0≤t0≤t≤t0+τ时,则有 (22) 式(21)证明了式(16)在0≤t≤τ时是成立的。假设当t∈[0,kτ]时,式(22)成立。在式(22)中令t0=t-τ,可得 (23) 当t∈[r,(k+1)τ]时,t-τ∈[0,kτ]。根据引理2,将式(16)代入式(23)中,有 (24) 证毕。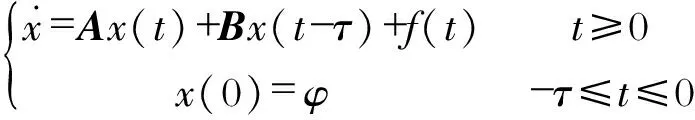
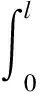
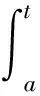
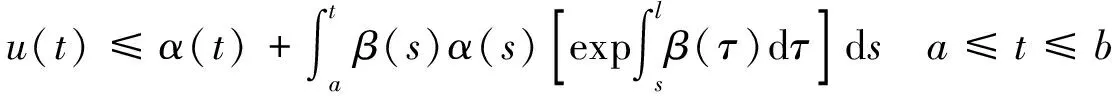
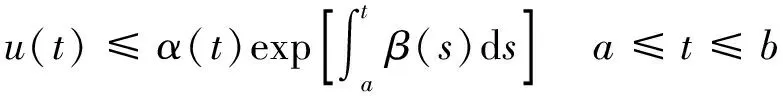
2 永磁同步电机时滞分数阶PID控制建模
2.1 永磁同步电机矢量模型

2.2 时滞分数阶PID控制
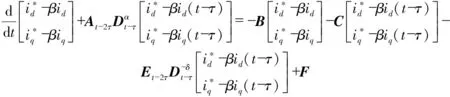
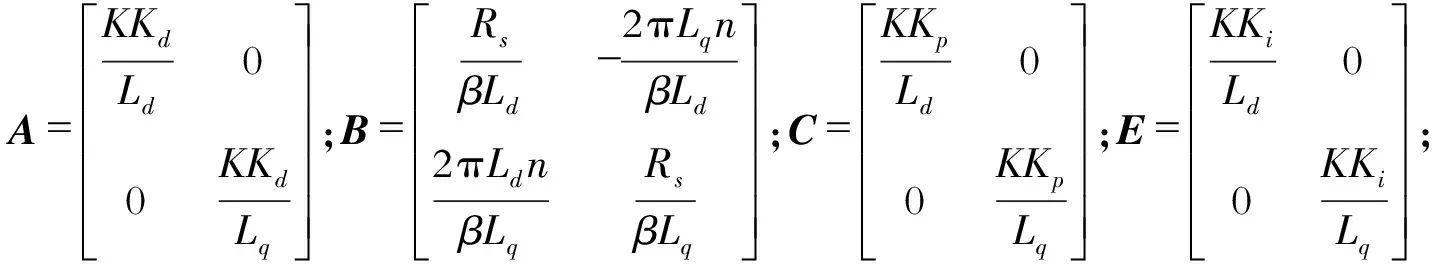
3 主要结果
3.1 解的存在唯一性
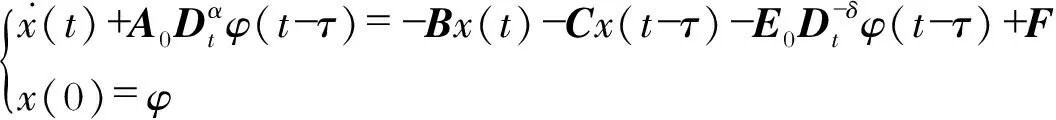
3.2 解的指数估计
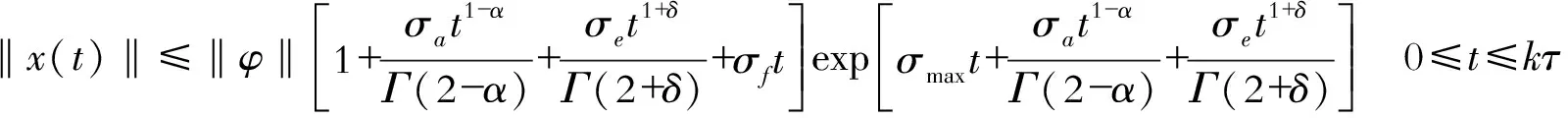

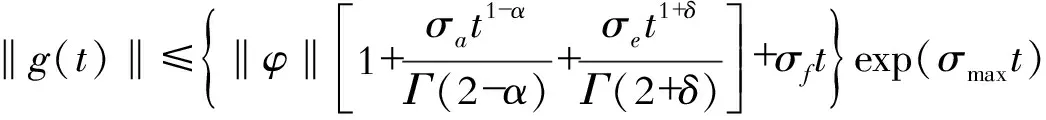
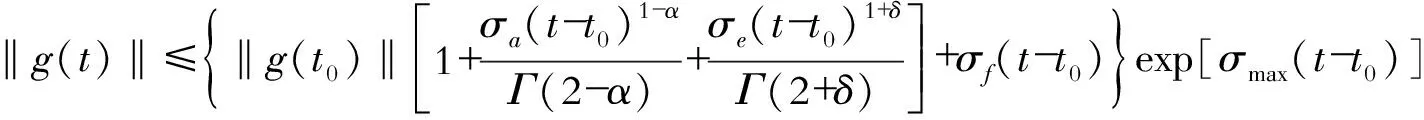
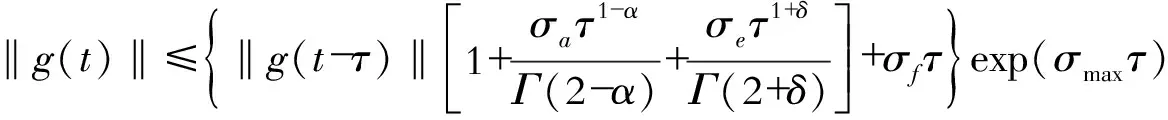
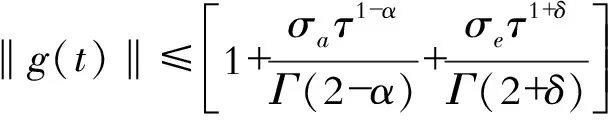
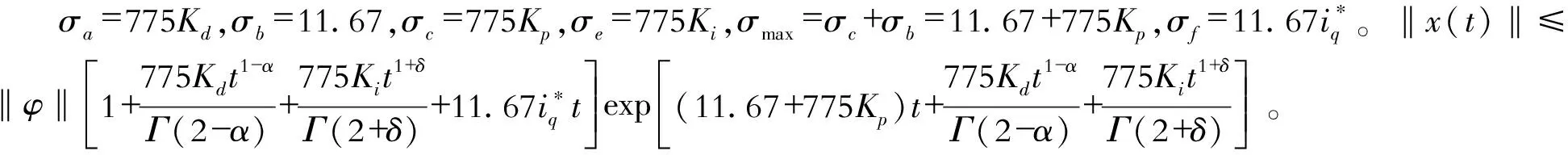
4 结论