数形结合在初中函数教学中的应用

曾国锋

进入初中阶段，函数内容是重点知识，也是数学教学中的难点，同时又是“数形结合”思想方法体现得很充分的一个内容，数形结合思想的运用能够为函数问题的解决提供便利，本文从初中数学函数分析入手，对数形结合法在函数问题中的應用策略进行探讨，介绍一些解题技巧和教学方法。

一、利用数形对比学习函数图像的性质以及函数的变换

函数图像可以直观的研究函数性质，从图像上可以观察函数的变化规律，整体上把握函数的性质，但是难以深入局部和细节。而解析式可以对函数的性质进行详细表达，但理解起来比较抽象，不够直观。所以我们通常会把函数图像和解析式结合起来，研究函数的性质，通过数形结合，简单，明了。如从一条具体的抛物线，指出顶点坐标，对称轴，开口方向，在y轴上的截距，与x轴的交点坐标，函数值y随x增大而增大的x的取值范围，y随x增大而减小的x的取值范围等。相反，从一条解析式也可以得出函数图像的有关性质。在讲授二次函数的图像性质时，数形结合研究函数贯穿二次函数讨论的始终，对于最简单的二次函数y=x2的研究就是从画这个函数的图像开始，然后通过图像了解它的性质，其后的二次函数的研究，也都展现了从解析式到图像，从图像到性质的过程。

在学习二次函数的图像与性质时，可以从简单到复杂，从特殊到一般的顺序通过数形结合进行讨论，每一个解析式的特点在坐标系上如何变化，图像上的特点在解析式上表现在哪些数，有哪些规律？通过图形与数的对比总结出特点，如：y=x2的图像最基础，开口向上，对称轴是y轴，顶点坐标是（0，0），比较y=x2+1和y=x2-1的图像特点，“数”上与y=x2比较多了加1或者减1，“图”上如何变化呢，让学生观察，得出：形状不变，位置是向左或者向右移动了一个单位而已。再探讨y=（x+1）2和y=（x-1）2的图像特点，从数形上对比得出：在y=x2的图像基础上，形状不变，只是位置向上或者向下移动了一个单位而已。最后综合起来探讨y=（x+1）2+1的图像特点，从“数”上看有什么变化，从“图”上看有哪些变化，通过图形结合，可以对整个二次函数的图像特点一目了然，总结出二次函数的性质。

二、利用数形结合理解一次函数与方程

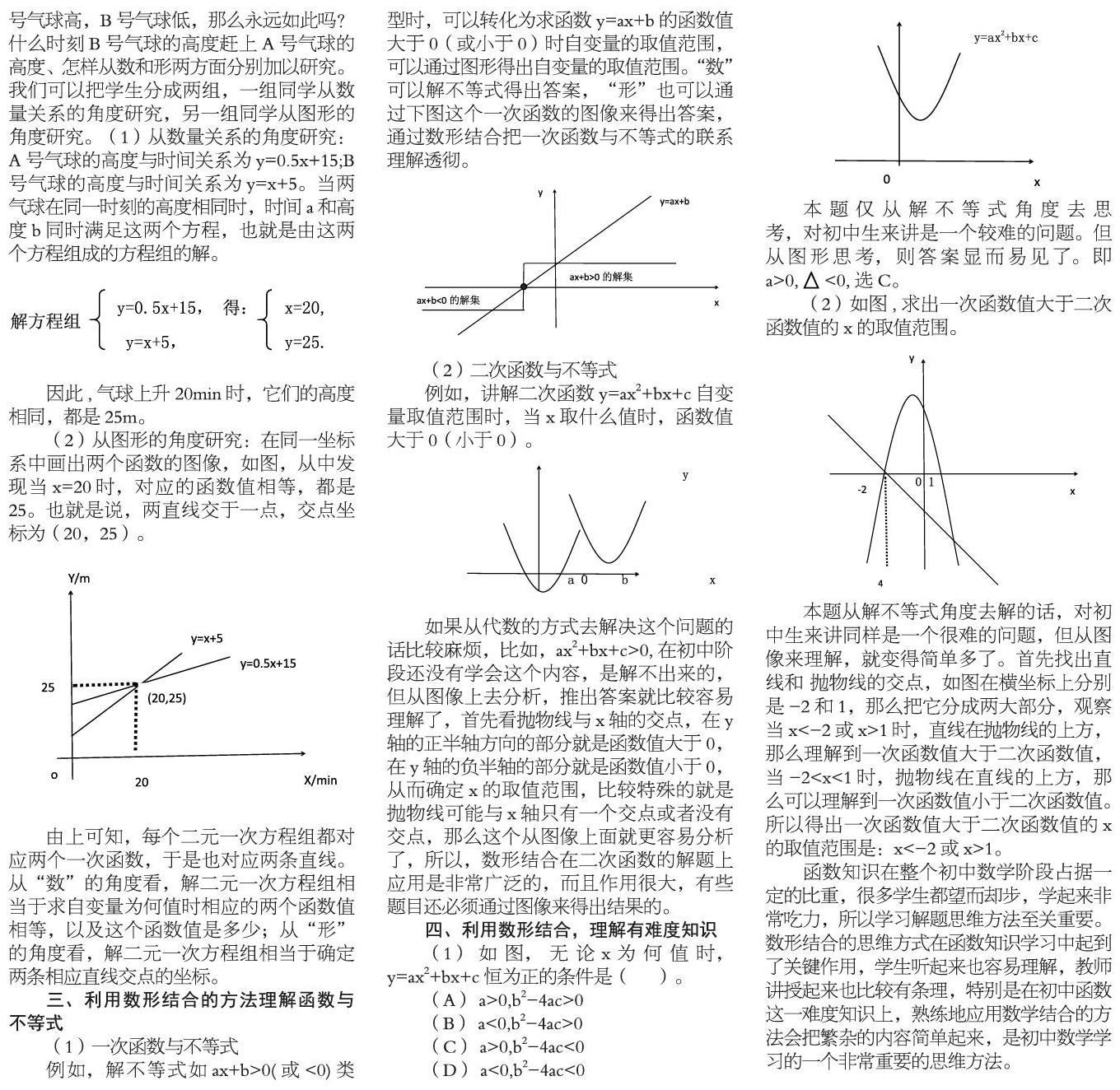
例如，讲解《一次函数与方程》问题3时，由于两气球上升的速度不同，开始时A号气球高，B号气球低，那么永远如此吗？什么时刻B号气球的高度赶上A号气球的高度、怎样从数和形两方面分别加以研究。我们可以把学生分成两组，一组同学从数量关系的角度研究，另一组同学从图形的角度研究。（1）从数量关系的角度研究：A号气球的高度与时间关系为y=0.5x+15;B号气球的高度与时间关系为y=x+5。当两气球在同一时刻的高度相同时，时间a和高度b同时满足这两个方程，也就是由这两个方程组成的方程组的解。

因此，气球上升20min时，它们的高度相同，都是25m。

（2）从图形的角度研究：在同一坐标系中画出两个函数的图像，如图，从中发现当x=20时，对应的函数值相等，都是25。也就是说，两直线交于一点，交点坐标为（20，25）。

由上可知，每个二元一次方程组都对应两个一次函数，于是也对应两条直线。从“数”的角度看，解二元一次方程组相当于求自变量为何值时相应的两个函数值相等，以及这个函数值是多少;从“形”的角度看，解二元一次方程组相当于确定两条相应直线交点的坐标。

三、利用数形结合的方法理解函数与不等式

（1）一次函数与不等式

例如，解不等式如ax+b>0（或<0）类型时，可以转化为求函数y=ax+b的函数值大于0（或小于0）时自变量的取值范围，可以通过图形得出自变量的取值范围。“数”可以解不等式得出答案，“形”也可以通过下图这个一次函数的图像来得出答案，通过数形结合把一次函数与不等式的联系理解透彻。

（2）二次函数与不等式

例如，讲解二次函数y=ax2+bx+c自变量取值范围时，当x取什么值时，函数值大于0（小于0）。

如果从代数的方式去解决这个问题的话比较麻烦，比如，ax2+bx+c>0，在初中阶段还没有学会这个内容，是解不出来的，但从图像上去分析，推出答案就比较容易理解了，首先看抛物线与x轴的交点，在y轴的正半轴方向的部分就是函数值大于0，在y轴的负半轴的部分就是函数值小于0，从而确定x的取值范围，比较特殊的就是抛物线可能与x轴只有一个交点或者没有交点，那么这个从图像上面就更容易分析了，所以，数形结合在二次函数的解题上应用是非常广泛的，而且作用很大，有些题目还必须通过图像来得出结果的。

四、利用数形结合，理解有难度知识

（2）如图，求出一次函数值大于二次函数值的x的取值范围。

本题从解不等式角度去解的话，对初中生来讲同样是一个很难的问题，但从图像来理解，就变得简单多了。首先找出直线和 抛物线的交点，如图在横坐标上分别是-2和1，那么把它分成两大部分，观察当x<-2或x>1时，直线在抛物线的上方，那么理解到一次函数值大于二次函数值，当-21。

函数知识在整个初中数学阶段占据一定的比重，很多学生都望而却步，学起来非常吃力，所以学习解题思维方法至关重要。数形结合的思维方式在函数知识学习中起到了关键作用，学生听起来也容易理解，教师讲授起来也比较有条理，特别是在初中函数这一难度知识上，熟练地应用数学结合的方法会把繁杂的内容简单起来，是初中数学学习的一个非常重要的思维方法。