“阿氏”隐圆的妙用

蔡于兵

[摘  要] 在许多平面解析几何的考题中，阿氏隐圆经常被“植于”题中，且不易被学生发现.文章对一道以阿氏隐圆為背景的线段最小值问题进行探究.

[关键词] 圆;线段;最小值

认识阿氏隐圆

在平面上给定相异两点A，B，设P点在同一平面上，且满足 =λ，当λ>0且λ≠1时，P点的轨迹是个圆，这个圆我们称作阿波罗尼斯（Apollonius）圆，简称阿氏圆. 这个结论称作阿波罗尼斯轨迹定理.

此定理就是讲，如果平面上的动点到两个定点的距离之比为定值，且定值不为1时，动点的轨迹就是阿氏圆，由于此圆隐藏于题设条件中，故一般称为阿氏隐圆，且通过具体的坐标代入运算后，我们会发现此圆的圆心与两个定点在同一直线上.

考题再现

题目：在平面四边形ABCD中，∠BAD=90°，AB=2，AD=1，若 · + · =  · ，则CB+ CD的最小值为___.

题意分析：对于本题，我们首先要根据题意作出相应的简图，不难发现，题中B，A，D三点的位置是相对固定的，变化的是点C，那么点C位置该如何确定呢？只有一条路可走，即通过对题设中所给的向量等式进行处理，解出点C的轨迹，而对于本题中向量等式的处理，无非两种途径：一是进行向量的转化;二是建坐标系，进行相关坐标运算.

有了点C的轨迹之后，再考虑CB+ CD的最小值问题.

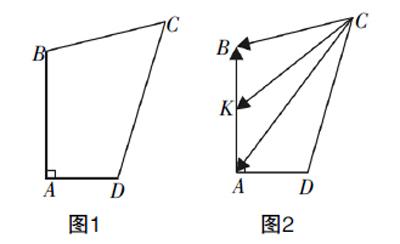
解题思路1：（向量转化法）作出大致图形，如图1所示，注意到向量等式 · + · =  · 的左边可以简化处理，即 · + · = ·（ - ）= · = 2，

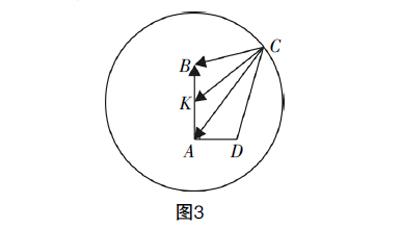
对于等式右边，可以取AB的中点K，如图2所示，有  · = （ + ）·（ + ）= （ - ）·（ + ）= （ 2- 2），于是 2= （ 2- 2），即4= （ 2-1），得到 =2，所以点C的轨迹是以点K为圆心，2为半径的圆，如图3所示.

图3

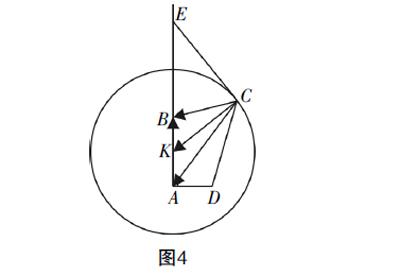
对于问题待求“CB+ CD”的值，如何将CB，CD这两项系数转换成相等呢？此处就可以根据阿氏圆的定义，构造出满足阿氏圆的两个定点，由于两定点与圆心在同一直线上，这里我们就可以在射线AB上取点E，如图4所示，若能使得 =2，那么CB= CE，如此一来，CB+ CD= CE+ CD= （CE+CD），只需求出CE+CD的最小值即可.

那么点E的具体位置怎么确定呢？在△CKB与△EKC中，已经有 =2，∠CKB=∠EKC，若再满足 =2，那么△CKB∽△EKC，则有 =2. 这样，我们就可以确定点E的具体位置了，即在射线AB上取点E，使得EK=2CK=4，此时AE=5，CB= CE，则CB+ CD= CE+ CD= （CE+CD）≥ DE= .

解题思路2：（坐标运算法）建立如图5所示的平面直角坐标系，因为AB=2，AD=1，那么可得相关点的坐标A（0，0），B（0，2），D（1，0）. 可设点C（x，y），则由 · + · =  · 可得，（0，2）·（x，y）+（0，-2）·（x，y-2）= （-x，-y）·（-x，2-y），整理有x2+（y-1）2=4，所以点C的轨迹是以K（0，1）为圆心，2为半径的圆，如图6所示.

下面再来处理待求问题“CB+ CD”的值，与思路1一样，根据阿氏圆的定义，构造出满足阿氏圆的两个定点，将CB，CD这两项系数转换成相等. 由于两定点与圆心在同一直线上，所以可以在射线AB上取点E（0，e），使得 =2，那么CB= CE，则CB+ CD= CE+ CD= （CE+CD），只需求出CE+CD的最小值即可. 此处可取点C为特殊点来求解，不妨取点C（0，3），那么根据 =2，有 =2，解得e=5，所以E（0，5），如图7所示，故CB+ CD= （CE+CD）≥ DE= .

点评：在解题思路1中，取出线段AB的中点K来协助转化已知的向量等式，从而得出点C的轨迹是圆，这是第一个关键点. 第二个关键点则是根据阿氏圆定义，构建符合比值要求的圆外定点E，这其中运用相似三角形的性质也是至关重要的. 在解题思路2中，由于建立了平面直角坐标系，所以处理已知向量等式时能较轻松地得出点C的轨迹是圆，接下来转化点B时，采用特殊点C（0，3）来求解点E的坐标，体现了数学中的一般与特殊的转化思想. 在本题的两种解题思路中，我们都离不开一条中心主线——阿氏隐圆，利用其将问题中已知的两个定点中的一个定点B转换成另一个点E，并且恰好保证所求距离之和中的两项的系数相等，进而再根据平面上“两点之间线段最短”这一结论来求最小值.

考巩固提高

题目：已知点P是圆O：x2+y2=25上任意一点，平面上有两个定点M（10，0），N ，3，则PN+ PM的最小值为____

解题思路1：首先根据题设条件作出简图，如图8所示，由于“PN+ PM”中两项的系数不相等，故我们可以将圆O：x2+y2=25理解成阿氏圆，根据阿氏圆的定义，构造出满足阿氏圆的两个定点，将PM，PN这两项系数转化成相等的系数. 因为两定点与圆心在同一直线上，所以可以在位于圆内的x正半轴上取点T（t，0），使得 = ，则PT= PM，且PN+ PM=PN+PT. 此处，不妨取圆O上的特殊点P（5，0）来解出T（t，0），即由 = 可得， = ，解得t= ，则T ，0，如图9所示，所以PN+ PM=PN+PT≥NT=5，故PN+ PM的最小值为5.

图9

点评：在本题的解析中，需要将所求问题PN+ PM中两项的系数转化为相等，所以将已知圆理解成阿氏圆，去构造定点T是解决问题的关键所在，而在求点T的坐标时，将点P特殊化是至关重要的.

解析思路2：将圆O：x2+y2=25理解成阿氏圆，则可在x轴上取点T（t，0），假设P（x，y），且使得 =λ，代入坐标有 =λ，将此式整理后，可得（λ2-1）x2+（λ2-1）y2+（20-2tλ2）x+λ2t2-100=0. 又因为x2+y2=25，所以有

（20-2tλ2）x+λ2（t2+25）-125=0，故20-2tλ2=0，λ2（t2+25）-125=0，解得λ=2，t= ，所以 =2，因此PN+ PM=PN+PT≥NT=5，故PN+ PM的最小值为5.

点评：本解运用了待定系数法求解，从阿氏圆的定义出发，构建出含参数的圆O的方程，然后再比照已知圆方程，求出参数，只是解析中有烦琐的代数运算，稍不注意，就有可能算错，因此计算时要慢算、细算.

在众多解析几何问题中，阿氏隐圆算是非常经典的问题之一，虽没有在高中教材中被明确提出，但是有隐藏在高中教材中的习题里，这里就不再列出来了. 由于阿氏隐圆在解题中有着广泛的应用，故教师在平时的教学活动中，要重视阿氏隐圆的教学，对有关阿氏隐圆的问题要及时帮助学生进行分类汇总，引导学生体会题中的意境，促进学生数学思维的发展和解题能力的提高.